一种基于模拟信息转换器的工业超声成像方法*

戴光智

(深圳职业技术学院 计算机工程学院，广东 深圳 5180552)

一种基于模拟信息转换器的工业超声成像方法*

戴光智

(深圳职业技术学院 计算机工程学院，广东 深圳 5180552)

有限新息率(FRI)模型是传统的采样理论与压缩感知相结合的信号采集新方案。FRI理论指出，具有FRI性质的信号，可由各个短脉冲信号的延迟时间和幅度进行完备的表示，而超声波的反射信号可以看成由一系列不同延迟时间和幅度的高斯脉冲信号的叠加，因此可以采用FRI模型有效减少采样数据和采样频率。在压缩感知理论的框架之下，以FRI理论为模型，并且结合相控阵超声波成像特点以及模拟信息转换器两种结构的特点，提出了一种适用于超声波成像的新型信号采样方法——基于滤波的模拟信息转换器的信息采样方法，并以Field II为仿真工具，对工业超声成像的实测数据采用该方法进行处理，取得了较好的效果，为FRI理论在超声波工业检测系统中的应用做了有益的理论探索和实测数据仿真。

模拟信息转换器；超声成像；压缩感知； FRI

0 引言

近年来，CANDES E等人提出了一种采样与压缩同步进行的理论——压缩感知理论(Compressive Sensing,CS)[1]，打破了传统的模拟信号采样固有的模式，以远低于香农采样率的优势而缓解传统的模拟数字转换器(Analog-to-Digital Converter, ADC)采集数据的压力，为现代数据采集提供了一种新的方式。有限新息率(Finite Rate of Innovation, FRI)模型是传统的采样理论与压缩感知相结合的采集信号的新方案，它最早由VETTERLI M等人[2]提出来。具有FRI性质的信号可以由各个短脉冲信号的延迟时间和幅度进行完备的表示。而这些短脉冲信号的延迟时间和幅度包含了源信号的有效信息。尽管VETTERLI M提出的FRI采样模型降低了采样频率，但其提高的空间还很大，由于其采样核的设计采用的是高斯函数，适用其函数的信号类型有限，仅限于狄拉克脉冲信号，随后又提出了一系列改进的采样核，如B-spline、E-spline[3]，尽管这些采样核恢复的信号类型不限于狄拉克脉冲，可以为分段信号，但当信号自由度高的时候重建效果并不理想，此后出现了SOS采样核[4]使重建效果得以改善。

模拟信息转换器(Analogue to Information Converter, AIC)是压缩感知理论设计测量矩阵的重要应用实现方式，在模拟信号到数字信号转换过程中可以实现远低于奈奎斯特门限以信息样点的采样，这样就构造了模拟信号直接信息采样的方法。常用的模拟信息转换器结构主要有两种：LASKA J N等人提出随机调制型AIC[5]，以色列ELDAR Y C等人提出调制宽带型(Modulated Wideband Converter, MWC)[6]。随机调制型AIC已在超声成像、雷达信号和地震探测等领域得到了广泛应用，如中国科学院吕燚等人将此结构应用到医学超声成像来降低超声信号的采样率；西安电子科技大学石光明等人将随机调制型AIC应用于雷达系统中[7]。调制宽带型AIC实现结构采用的是多通道采集模式，其应用范围仅限于多频带信号处理当中,如韩国蔚山大学TAN L T等人将此结构应用用于无线网络协作频谱感知[8]，因其要求信号的局限性不能在其他领域中得到广泛应用。

超声波工业成像系统的反射信号可以看成由一系列不同延迟时间和幅度的高斯脉冲信号叠加而成。因此，超声波工业成像系统的反射信号具有FRI性质，可以利用FRI模型中的采样方法进行信号采样和重建。不幸的是，现有的FRI信号采集方法在对高频信号进行采样时并不稳定。而通常超声波工业成像系统的反射信号的频率很高，现有的FRI模型并不能很好地应用在超声波工业成像系统中，因此，基于FRI采样模型，结合超声成像的特点以及模拟信息转换器两种结构的特点，提出了基于SOS滤波器的模拟信息转换器模型，对该模型进行深入的理论推导，并根据此模型提出了基于滤波的模拟转换器超声成像算法，最后经过实验仿真验证了本算法的可行性。

1 基于SOS滤波器的模拟信息转换器结构模型

基于滤波的模拟信息转换器结构模型相对于随机调制AIC和调制宽带AIC具有设计简单、确定性强、采样的数据量少而且速度快的特点，主要由滤波器、低速采样器和FFT快速傅里叶变换计算模块构成，结构模型如图1所示。

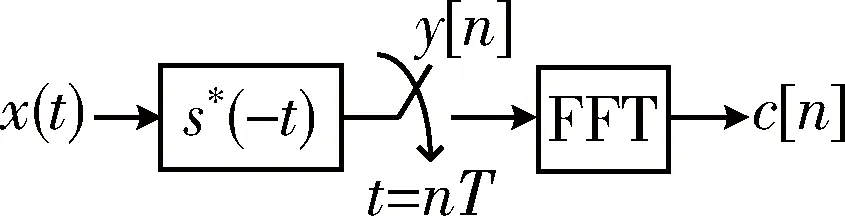
图1 基于滤波的模拟信息转换器结构框图

首先分析此模型用到的滤波器函数s*(-t)，称为SOS滤波器，此滤波器的特点是在频域不受带宽限制，并且s*(-t)=s(t)具有共轭反对称性，其频域由一组sinc函数的和构成的：

(1)

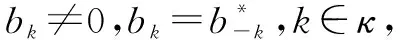
(2)

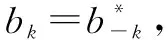
(3)

若将此滤波器由频率域转换为时间域，则有：

(4)

由式(4)可以看出此滤波器具有累加器和低通滤波的双重特性，并且能够通过稀疏窗函数来调节滤波器的抗噪声能力。

由图1可知基于滤波的模拟信息转换器采集过程是源信号下x(t)通过滤波器s*(-t)后以低频率1/T采样，将采样的值用快速傅里叶变换(FFT)得到向量c[n]，具体数学表达式如下：

(5)

对采样得到的值y[n]做快速傅里叶变换可以得到：

(6)

可以将式(6)写成如下矩阵形式：

c=V(ts)Sx

(7)

其中c={c[1],c[2],…,c[N]}，ts={nT:n=0,…,N-1}(T=τ/N),矩阵V是M′N的范德梅德矩阵，这里第(k,j)的元素为ej2πknT/τ,要求M3N，则V是列满秩，矩阵S为M′N的单位正交对角矩阵，其中第k个对角元素为S*(2πk/τ)。令感知矩阵A=V(ts)S,大小为M′N，式(7)可以重写为：

c=Ax

(8)

如果N=M，矩阵A满秩，则A为可逆的，式(8)可以重写为x=A-1c，可以看出对信号通过SOS滤波器滤波后所得到的采样向量c乘以A-1，就能得到傅里叶系数矩阵x，只要保证测量值M32L，可用谱估计方法如Annihilating Filter Method[9]或Pencil Matrix[10]求出源信号的有效信息即幅度与延时时间，由此可见，只需要采集M(M32L)个值就可以对信号进行重构。

如果N>M，由式(8)可知所表达的是一个欠定方程组，可以转化为压缩感知理论重构问题进行求解，为了重建稀疏度为L(L≼N)的N维向量x，可以用子空间分析将其投射到N个正交向量的子集，利用感知矩阵A来求出向量x，因感知矩阵A是由傅里叶变换构成的单位正交对角矩阵和范德蒙矩阵组成，在其正交基中随机选出M行作为测量矩阵A，只要满足K3CL(logN)4，其中C为常量，此时A就满足RIP特性，具有很高的可靠性，最后可以用压缩感知恢复算法l1凸优化算法求解傅里叶系数矩阵x。

2 超声成像算法

为了解决超声成像过程中的换能器采样率高和数据存储量大等问题，可利用基于滤波的模拟信息转换器结构模型来降低超声回波采样率，从而减少超声数据的存储量。假设超声成像区域无明显的衰减，采集信号用的是线性换能器阵列，成像区域可由一系列散射点组成，每个阵元接收的探测回波信号满足波形不变性，而在超声成像中，为了提高信噪比和灵活控制成像，通常将多个单阵元接收到的信号进行波束合成来得到波束回波信号。算法框图如图2所示，M个线性阵元探测到的回波信号分别经过基于滤波的模拟转换器进行采样，由每个阵元单通道的采样值，通过谱估计算法或压缩感知恢复算法对每个通道的回波信号重构，最后将多通道重构的回波信号累加从而得到目标波束合成信号。

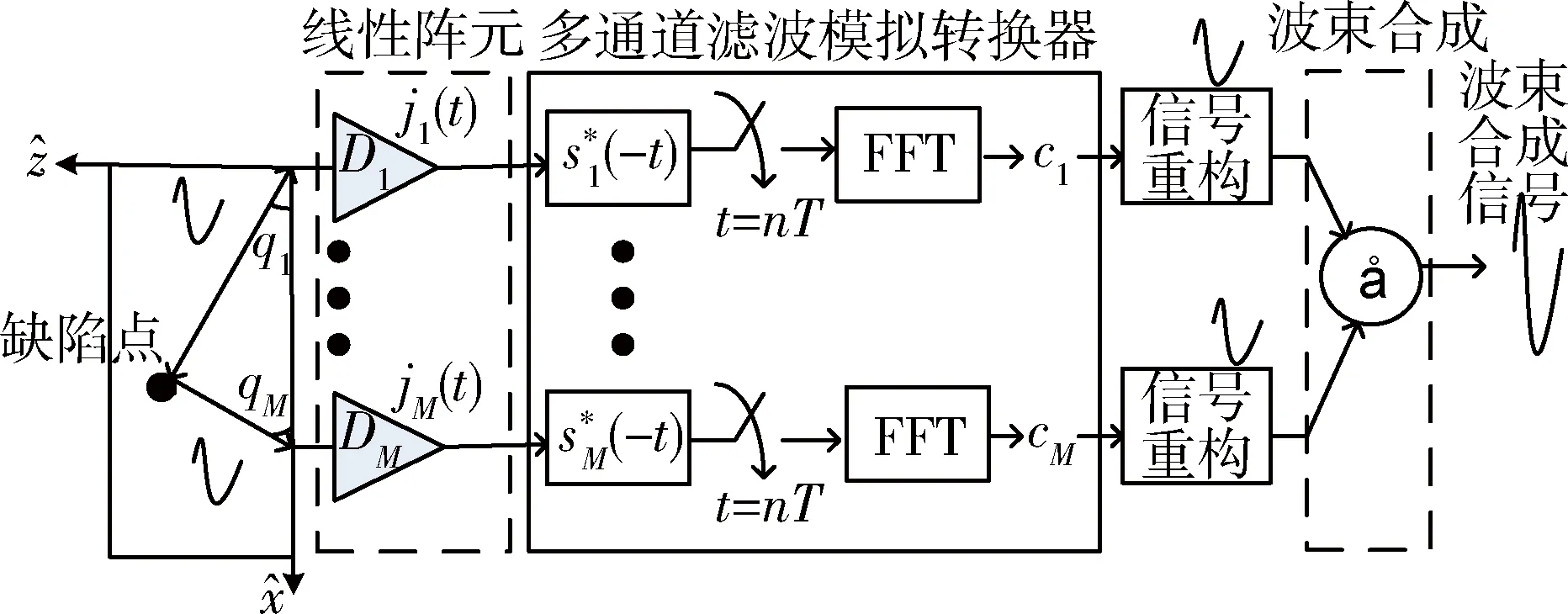
图2 基于滤波的模拟信号转换器的超声成像算法框图

多通道换能器线性阵元用基于滤波的模拟信息转换器对目标缺陷点发射的回波信号进行采集，假设第m个阵元接收的回波信号可表示为一系列点目标回波的加权组合：

(9)

(10)

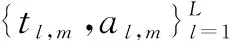
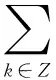
(11)

将式(11)以矩阵形式表示如下：

c=V(ts)Sx=Ax

(12)

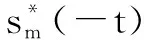
(13)

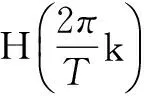
如果将式(13)重新写成矩阵形式，则：

φ=HVb=Aa

(14)

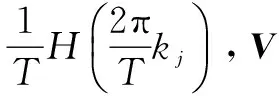
为了准确地定位目标点，如图2所示，波束合成信号是多通道换能器阵元通过滤波的模拟信息转换器重构的回波重构在偏转角为q的方向上构建波束合成信号为f(t;q)，则有：

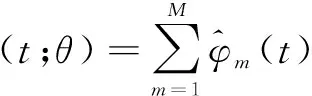
(15)

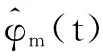
由上面分析可知，基于滤波的模拟信息转换器超声成像算法主要是利用少量的值对波束信号重构。首先线性换能器阵元单通道通过基于滤波的模拟转换器直接对目标点发射的回波信号在时域上进行有效的采样。然后将每个通道获取的信号离散序列值进行有效处理，通过转置或压缩感知恢复算法求出波束回波信号的傅里叶变换值。进而通过谱估计方法或压缩感知恢复算法得出每个通道回波信号反映目标散射点的未知信息，最后将每个通道恢复的回波信号进行信号合成，得到波束回波信号。可见，本算法应用在超声成像上既可以减少采样值，又能够增强回波信号的幅度值，增加了探测目标点的准确度。

3 算法仿真

算法仿真主要是用模拟超声仿真工具Field II[11]来实现。将提出的算法对超声回波信号进行离线处理，主要在均方误差(MSE)、相对重建误差(RE_ERR)等指标上与传统成像方法对比，仿真为提出的模型结构应用在线性换能器单阵元接收回波信号成像情况。

均方误差(MSE)定义为：

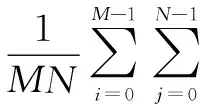
(16)

相对重建误差(RE_ERR)定义为：

(17)

仿真使用单探头发射激励脉冲到目标区域，在重构目标回波信号方面，将提出的基于滤波的AIC与传统成像方法以及随机调制型AIC进行对比。仿真参数为：有效的换能器线性阵元数目为8个，阵元高度和间距分别设置为5 mm、0.25 mm。发射的激励脉冲为双周期中心频率0.5 MHz的正弦信号，超声波速为1 540 m/s，采样频率为4 MHz，线性换能器的单位脉冲响应与发射的激励脉冲信号一样，并且经过汉宁窗函数调制。在线性阵元选取其中的一个作为单通道采集回波信号进行实验分析。

实验模型结构如图3所示，目标散射点分布在目标区域当中，超声成像系统发射接收中央控制器发射激励脉冲，通过单探头进入目标区域中，散射点对激励信号产生发射，由于对目标点的探测反射的回波信号弱，为了使实验效果明显，需要增加时间增益控制器来提高回波的强度，获取到的回波信号分别经过基于滤波的模拟转换器和随机调制型AIC来进行对比成像。实验仿真结果如图4和图5所示，其中图4(a)为发射的激励单脉冲信号h(t)，是一个中心频率为0.5 MHz的双周期正弦信号，散射点回波信号由L=16个激励脉冲信号组合表示，如图4(b)，设一个周期τ=1内回波信号离散化长度为396，滤波器的参数bk赋值为长度为M的汉明窗系数，取κ的连续取值区间κ={-16,…,16}，则M=|κ|=33。图5给出了回波信号经过提出的模拟转换器中滤波输出采样结果，可以看出原始回波信号通过滤波器输出后形状并没有多少变化，只是幅度变大了。对滤波输出的信号进行了33次有效采样，可以根据这33个采样值求出回波信号的傅里叶变换的系数，进而对回波信号进行重构。

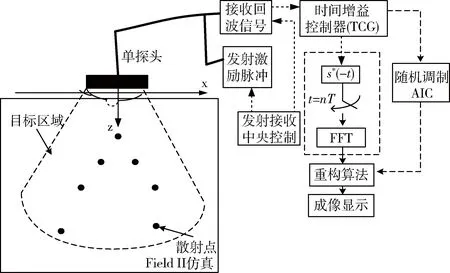
图3 基于滤波的模拟信息转换器的单通道超声成像实验框图

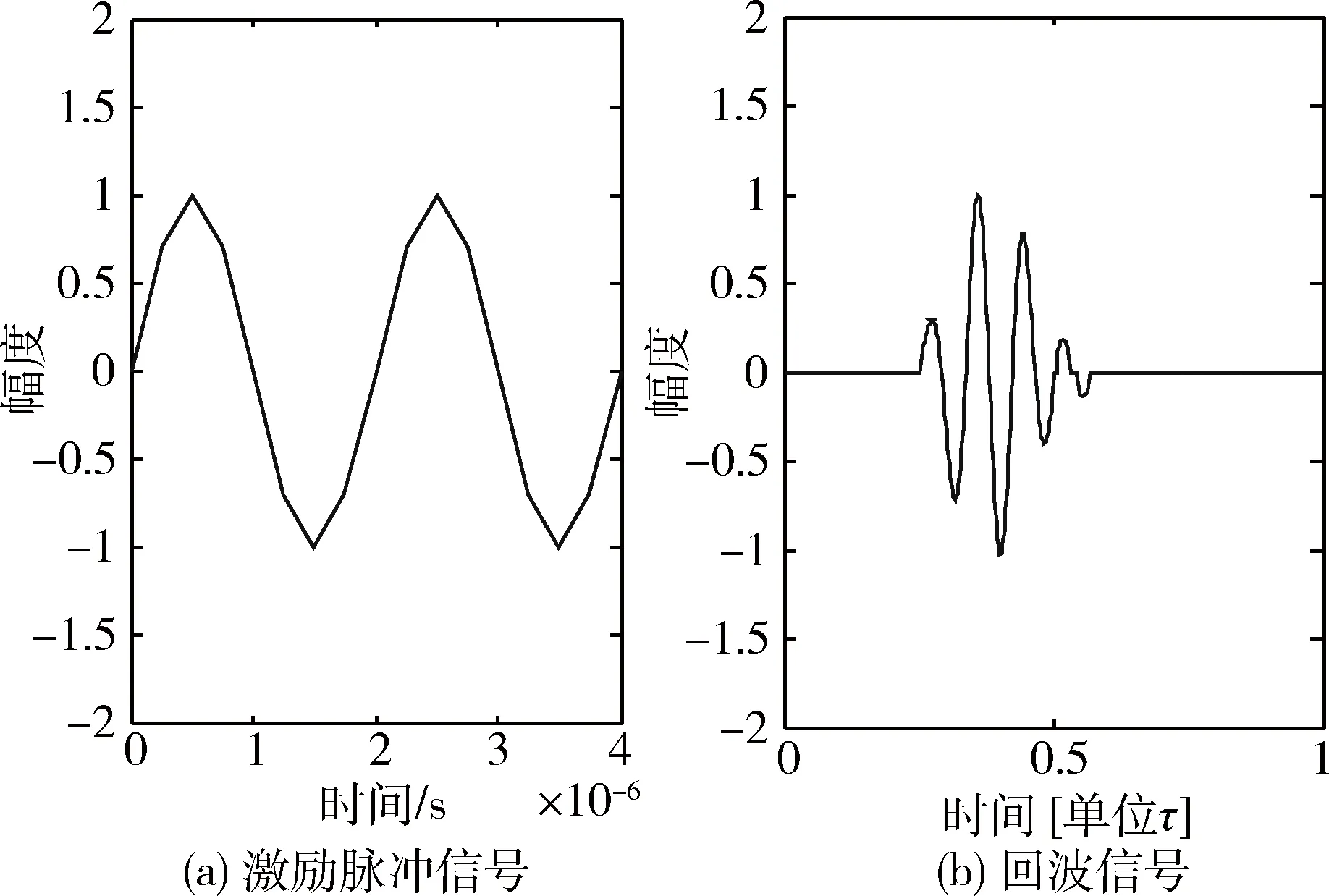
图4 激励脉冲信号与回波信号仿真结果

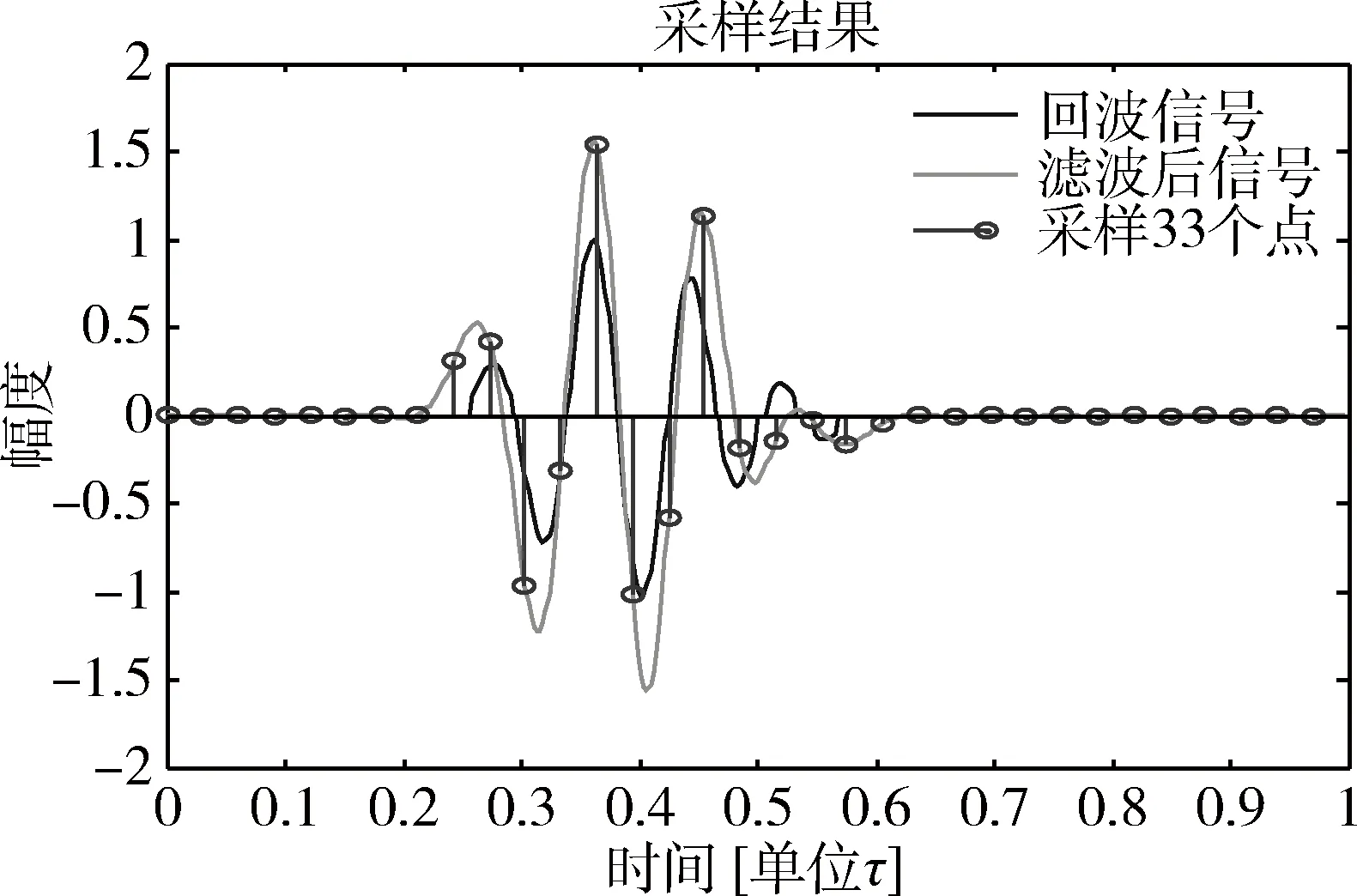
图5 滤波器对回波信号滤波情况实验结果

图6 基于滤波AIC与随机调制型AIC重构效果

图6比较了基于滤波AIC和随机调制型AIC重构的效果，其中图6(a)是通过基于滤波AIC采样得到回波信号的傅里叶变换系数，根据谱分析恢复算法Annihilating Filter得出的重构信号与原始信号作比较的结果。可以看出重构信号与输入的回波信号几乎一样，定量计算本模型的重构均方误差为MSE= 0.003 4。为了进一步说明此结构重构性能，实验对比了随机调制型AIC模型对回波信号采样220个点进行恢复，重构效果如图6(b)所示,恢复的回波信号包含很多噪声信息，定量分析通过此模型重构的信号与回波信号的均方误差为MSE= 0.104 5。由此可见，对长度为396个点的原始回波信号，基于滤波AIC只需采样33个点就能够很好地恢复，并且比随机调制型AIC对数据的处理方式重构效果要好。

4 结论

(1)基于FRI模型，提出一种基于模拟信息转换器的工业超声成像方法。

(2)仿真结果说明，基于滤波模拟转换器能够实现对超声回波信号的稀疏采样，在信号欠采样的情况下通过信息率的方式进行采样，能够很好地恢复，而且该结构简单,不需要过多的硬件，将压缩感知理论应用在超声成像中，为解决高采样带来的数据量大的问题提供一种新的思路。

(3)通过实验仿真可见，提出的基于滤波的模拟信息转换器模型能够有效对信号进行信息采样，并且只需要采样17个点就可以成功恢复长度为4 148的原始信号，这样大大降低了信号的采样率，而且本模型实现结构简单。因此，利用此结构来对超声回波信号进行采样，解决超声成像数据量的问题是可行的，是降低超声数据采集率的一种有效的新方法。

[1] CANDES E, WAKIN M. An introduction to compressive sampling [J]. IEEE Signal Process Magaane, 2008, 25(2):21-30.

[2] VETTERLI M, MARZILIANO P, BLU T. Sampling signals with finite rate of innovation [J]. IEEE Transactionson Signal Processing, 2002, 50(6):1417-1428.

[3] DRAGOTTI P L, VETTERLI M, BLU T. Sampling moments and reconstructing signals of finite rate of innovation: shannonmeets strang-fix[J]. IEEE Transactions on Signal Process, 2007,55(5):1741-1757.

[4] BURSHTEIN A, BIRK M, CHERNYAKOVA T, et al. Sub-nyquist sampling and fourier domain beamforming in volumetric ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectronics, and Frequency Control, 2016,63(5): 703-716.

[5] LASKA J N, KIROLOS S, DUARTE M F, et al. Theory and implementation of an analog-to-information converter using random demodulation[C]. IEEE International Symposium on Circuits and Systems, ISCAS 2007, 2007: 1959-1962.

[6] MISHALI M, ELDAR Y C. From theory to practice: sub-nyquist sampling ofsparse wideband analog signals[J]. IEEE Journal on Selected Topics in Signal Processing, 2010, 4(2): 375-391.

[7] Shi Guangming, Lin Jie, Chen Xuyang, et al. UWB echo signal detection with ultra-low rate sampling based on compressed sensing[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2008, 55(4): 379-383.

[8] TAN L T, KONG H Y. A novel and efficient mixed-signal compressed sensing for wide-band cognitive radio[C]. International Forum on Strategic Technology (IFOST), Ulsan, Korea. USA: IEEE, 2010: 27-32.

[9] STOICA P, MOSES R. Introduction to spectral analysis[M]. EnglewoodCliffs, NJ: Prentice-Hall, 2000.

[10] SARKAR T K, PEREIRA O. Using the matrix pencil method to estimatethe parameters of a sum of complex exponentials[J]. IEEE Antennas and Propagation Magazine, 1995,37(1): 48-55.

[11] LUSTIG M, DONOHO D, PAULY J M. Sparse MRI: the application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 2007,58(6): 1182-1195.

A industrial ultrasound imaging method based on analogue to information converter

Dai Guangzhi

(School of Computer Engineering, Shenzhen Polytechnic, Shenzhen 518055, China)

The Finite Rate of Innovation(FRI) theory model is a new signal sampling scheme combining traditional sampling theory with compressive sensing. It states that a signal with FRI property is perfectly reconstructed after sub-Nyquist sampling. It has been shown that a much more significant sample reduction may be obtained by applying FRI to industrial ultrasound imaging system. Under the framework of Compressed Sensing theory, we propose a new sampling approach based on FRI theory——a filter based Analogue to Information Converter(AIC). And using Field II as a simulation tool, we process ultrasound imaging data using this techniques, obtain better result, and make some exploration and research on FRI theory in the application of ultrasonic industrial testing system for the future.

analogue to information converter(AIC); ultrasound imaging; compressed sensing(CS); finite rate of innovation(FRI)

国家自然科学基金(61671309)；广东省自然科学基金(10451805501006279，S2011010004487)；中国博士后科学基金(2012M511551)；深圳市科技基础布局项目(JCYJ20160428092447867)；广东省科技计划项目(2013B010401041)

TP274.2

A

10.19358/j.issn.1674- 7720.2017.16.014

戴光智.一种基于模拟信息转换器的工业超声成像方法[J].微型机与应用，2017,36(16)：48-52.

2017-04-24)

戴光智(1974-)，男，博士，副教授，主要研究方向：超声成像、图像处理等。E-mail：daiguangzhi@szpt.edu.cn。