基于GBDT的个人信用评估方法

王 黎，廖闻剑

（1.武汉邮电科学研究院 湖北 武汉 430074；2.烽火通信科技股份有限公司 南京研发部，江苏 南京 210019）

基于GBDT的个人信用评估方法

王 黎1，2，廖闻剑1，2

（1.武汉邮电科学研究院 湖北 武汉 430074；2.烽火通信科技股份有限公司 南京研发部，江苏 南京 210019）

近年来，个人信用评估问题成为信贷行业的研究热点，针对当前应用于信用评估的分类算法大多存在只对某种类型的信用数据集具有较好的分类效果的问题，提出了基于Gradient Boosted Decision Tree（GBDT）的个人信用评估方法。GBDT天然可处理混合数据类型的数据集，可以发现多种有区分性的特征以及特征组合，不需要做复杂的特征变换，对于特征类型复杂的信用数据集有明显的优势，且其通过其损失函数可以很好地处理异常点。在基于两个UCI公开信用审核数据集上的对比实验表明，GBDT明显优于传统常用的支持向量机（Support Vector Machine，SVM）以及逻辑回归（Logistic Regression，LR）的信用评估效果，具有较好的稳定性和普适性。

信用评估；分类算法；GBDT

信用风险分析在信贷行业起着非常重要的作用，对信贷申请者的准确信用评估可帮助信贷商家有效规避信用风险[1]。近年来，许多分类算法都被应用于个人信用评估，如线性判别分析[2]、LR[3]、K-NN最近邻算法、朴素贝叶斯、决策树[4]、神经网络[5]、SVM[6]等。这些方法中，神经网络多数情况下具有更高的评估准确率[7-8]，而关于支持向量机的研究则表明，支持向量机可以克服神经网络的不足，包括结构选择和小样本下泛化能力不足等问题。然而，在数据集维度较复杂时这些算法存在不能主动进行特征选择和特征组合的问题，因此准确率会受到无关维度的影响，甚至产生维度灾难[9]，并且在数据预处理中若不剔除异常点，也会对分类结果的准确率产生影响。如对于LR模型，特征组合非常关键，但又无法直接通过特征笛卡尔积解决，只能依靠人工经验，耗时耗力同时并不一定会带来效果提升。GBDT是一种通过将弱分类器组合来提升分类器性能的方法[10]。GBDT算法可有效解决自动进行特征选择和处理异常点问题，还能在一定程度上避免模型过拟合问题。在UCI两个公开信用数据集[11]上的对比实验有效验证了GBDT在个人信用评估应用上的适用性和稳定性。

1 GBDT介绍

GBDT模型在1999年由Jerome Friedman提出[12]，是决策树与Boosting方法相结合的应用。GBDT每颗决策树训练的是前面决策树分类结果中的残差。这也是Boosting思想在GBDT中的体现。具体算法思想如图1所示。

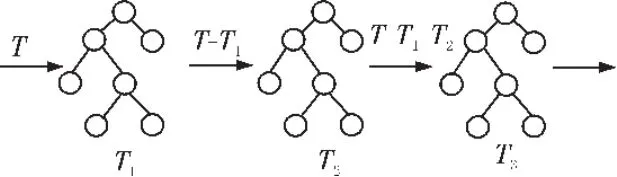
图1 GBDT算法思想示意图

从上图可以看出GBDT的训练过程是线性的，是无法并行训练决策树的。第一棵决策树T1训练的结果与真实值T的残差是第二棵树T2训练优化的目标，而模型最终的结果是将每一棵决策树的结果进行加和得到的。即公式（1）：

GBDT对于迭代求优常用的有两种损失函数。一种方式是直接对残差进行优化，另一种是对梯度下降值进行优化。从上图也可以看出，GBDT与传统的boosting不同，GBDT每次迭代的是优化目标，boosting每次迭代的是重新抽样的样本。下面，以一个二元分类为例，介绍GBDT的原理，如图2所示。

图2 二元分类示例图

对于一个待分裂的节点R，其输出值以不同样本y的平均值μ作为节点输出值，即公式（2）：

于是，节点的误差可以表示为公式（3）：

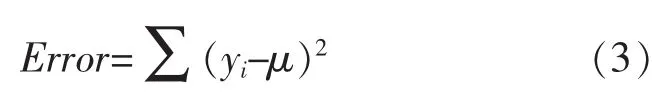
在节点分裂的过程中，需要选择分裂增益最大的属性进行划分，分裂增益G的计算方法如公式（4）：

采用方差作为损失函数，可以得到Sj，如公式（5）：

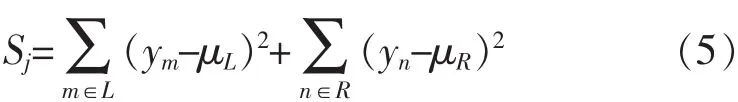
于是，每个节点分裂问题就变成寻找一个属性使分裂增益最大。分别将S，Sj展开，如公式（6）：

GBDT采用Shrinkage(缩减)的策略通过参数设置步长，避免过拟合。Shrinkage的思想认为，每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。Shrinkage仍然以残差作为学习目标，但对于残差学习出来的结果，只累加一小部分（step*残差）逐步逼近目标，step一般都比较小，如0.01～0.001，导致各个树的残差是渐变的而不是陡变的。本质上，Shrinkage为每棵树设置了一个权重，累加时要乘以这个权重。

2 基于GBDT的个人信用评估方法

2.1 信用数据的获取与预处理

由于我国个人征信体系刚刚起步，信用数据不易获得，因此本次实验基于UCI的两个公开信用审核数据集，分别是澳大利亚信用数据集和德国信用数据集。其中澳大利亚信用数据集的特征含义被隐去以保护数据源的机密性，而德国信用数据集包含以下指标，分别是 credit history、account balance、loan purpose、loan amount、employment status、personal information、age、housing和job等。这两个信用数据集的指标类型均包含数值型变量以及离散型变量。数据集的具体信息如表1所示。

表1 信用数据集

在获得这些信用数据集后，需要首先对这些原始数据进行一些预处理，如指标的数值化，标准化和缺失值填补等。数值化即把定性指标的属性值转换成数值，以UCI澳大利亚信用数据集为例，A1指标的两个属性值a和b，在本文中分别被数值化为0和1。虽然GBDT算法不需要对指标进行标准化处理，但对比实验中使用的SVM和LR算法中的目标函数往往认为数据集中的特征是标准化的并且具有同阶方差的，因此为避免某一指标因方差阶数太大而主导了目标函数，使得目标函数无法从其他特征进行学习，需要在预处理中统一对数据集指标标准化处理。本文将数据集处理成符合高斯分布的标准数据。对缺失值的填补，数值型变量采取中值填补方法，离散型变量采用众数填补。

2.2 基于GBDT方法的个人信用评估

根据前面介绍的GBDT的原理可知，GBDT分类模型的可调参数包括弱分类器（回归树）的个数M，每棵回归树的深度h，每棵树最大叶子节点数N，模型学习步长 step，损失函数（Loss Function），每个分裂节点最少样本数，每个叶子节点最少样本数，叶子节点样本的最小加权分数，子样本分数，以及分裂节点的特征数等。其中学习步长的范围为，是通过Shrinkage控制模型过拟合的参数，根据经验，较好的策略是选取较小的学习步长，对应的选取较多的回归树。树的深度和树的最大叶子节点参数都是来控制回归树大小的。如果定义树的最大深度为h，则会生成深度为h的完全二叉树，该树至多有2h-1个叶子节点和2h-1-1个分裂节点；如果定义树的叶子节点数k，则会通过best-first search生成树，该树的深度为k-1，有k-1个分裂节点。而后一种方法较前一种方法有更快的训练速度，代价是相对较高的训练误差,本课题训练样本数较少，暂不考虑训练时间的问题，为保证尽可能低的训练误差，本文选择设置树的深度h参数，而由于GBDT的 boosting特性，训练的每一步都会在上一步的基础上更加拟合原数据，模型是可以一定程度上保证较低的偏差（bias）的，那么为了同样保证较低的方差（variance），树的深度h的设置不需要太大。

GBDT可以通过优化损失函数来优化训练过程，本文使用Deviance作为GBDT的损失函数，那么对应的梯度为 I（yi=Gk）-pk（xi），pk表示样本xi属于第k个类别的概率，通过Softmax方法求得。因为有k个类别，所以得到k个系列的回归树，每个系列最终的预测值分别为f1（x），f2（x），…，fk（X），具体计算公式如（7）所示：

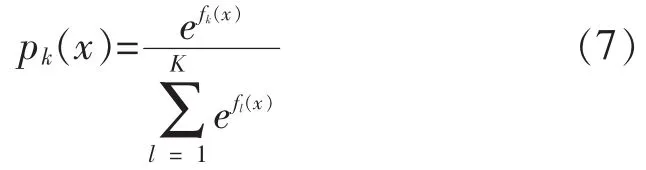
I（·）为指示函数。也就是当预测第k个类别的概率时，如果真实类别恰好为该类别，梯度为1-pk（xi），否则为-pk（xi）。所以后一棵树拟合的也就是之前预测值的残差。

3 实验结果与分析

本文基于UCI公开的澳大利亚信用数据集和德国信用数据集分别对支持向量机，逻辑回归，以及GBDT方法进行了信用分类性能比较实验。支持向量机采用的是 LIBSVM[13]，核函数（kernel function）是径向基核 （radial basis function，RBF）。 为了保证GBDT具有最好的分类性能，每次训练时都在训练集上利用5折交叉验证对GBDT中的参数进行网格搜索。实验中我们采取k折交叉验证（k-fold Cross Validation）的方式。所谓k折交叉验证指样本集被分成k组，轮流将其中的k-1组作为训练集，剩下1组作为测试集，实验结果取这k次实验结果的平均值。

我们在每个数据集上的实验分为5组，分别是5、10、15、20、25 折交叉验证， 实验结果如表 2 和表3。表2为基于澳大利亚信用审核数据集的各算法信用分类结果。表3为基于德国信用审核数据集的各算法信用分类结果。其中P、R、F分别表示Precision、Recall和 F-Score。

从表2和表3中可以看出，GBDT在澳大利亚和日本信用数据集上的各组实验中都获得了比LR和SVM更高的Precision、Recall和F-Score值。而对于信用数据集中正负例非常不平衡的德国数据集，虽然3种算法的F-Score均明显下降，但是GBDT方法依然保持相对较好的评估效果。在澳大利亚信用数据集上显示GBDT的平均F值比LR和SVM方法分别高出4.5％和6.7％；在德国信用数据集上GBDT的平均F值比LR和SVM方法分别高出12.8％和24.9％。从德国信用数据集来看，随着交叉验证的折数从 5变化到 25，LR的 F值变化了14.3％，SVM的F值变化了19％，GBDT的F值变化了10.4％。从图3中也能看出，GBDT相较于LR和SVM随实验折数的变化相对平稳。这说明GBDT相比于LR和SVM的信用分类效果不仅更好，并且具有较高的稳定性和有效性，对于正负例非均衡的数据集[15]也能保持相对较好的分类准确率。

表2 LR、SVM和GBDT在澳大利亚信用审核数据集上的评估效果（％）

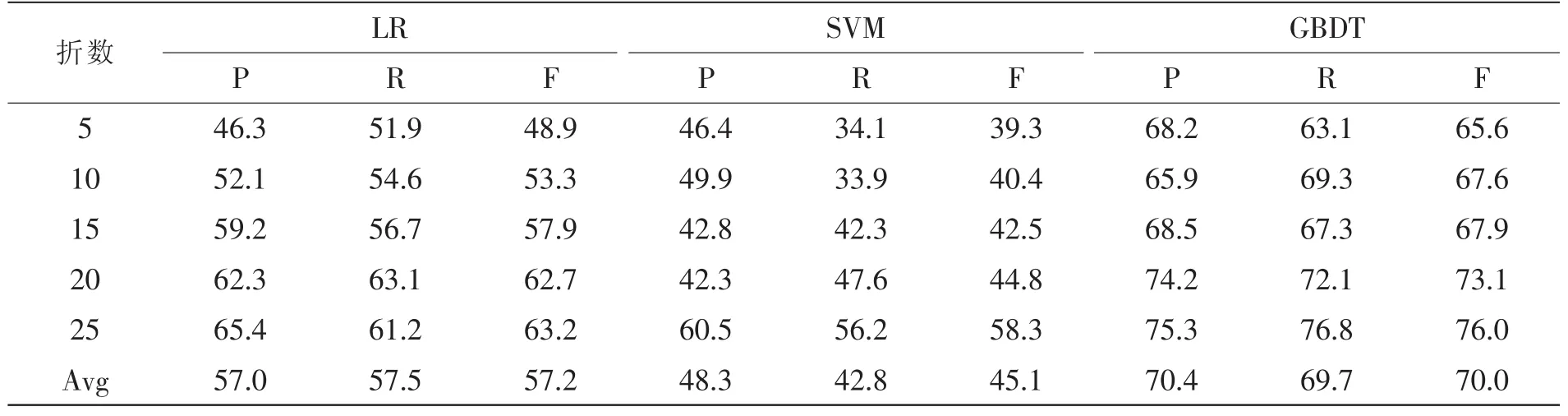
表3 LR、SVM和GBDT在德国信用审核数据集上的评估效果（％）

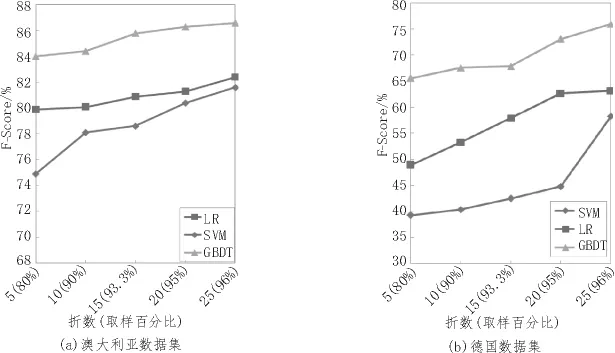
图3 LR、SVM和GBDT的F-Score随折数的变化

4 结论

文中针对当前应用于信用评估的分类算法大多存在只对某种类型的信用数据集具有较好的分类效果的问题，提出了基于GBDT的个人信用评估方法。实验表明在不同类型的信用数据集上，GBDT算法相对于工业常用的LR和SVM分类算法能保持较高的分类准确率，以及更好的稳定性和普适性。

[1]Burton D.Credit scoring， risk， and consumer lendingscapes in emerging markets [J].Environment and Planning A，2012，44(1):111-124.

[2]Basens B， Gestel T， Viaene S， et al.Benchmarking state-of-art classification algorithms for credit scoring [J].Journal of the OperationalResearch Society， 2003， 5(4):627-635.

[3]Sarlija N，Bensic M，Zekic-Susac M.Modeling customer revolving credit scoring using logistic regression survival analysis and neural networks[C]//Proceedings of the 7th WSEAS International Conference on Neural Networks， Cavtat， Croatia，2006.Stevens Point， Wisconsin， USA:WSEAS，2006:164-169.

[4]Bahnsen A，Aouada D，Ottersten B.Exampledependent cost-sensitive decision trees[J].Expert Systems with Applications， 2015， 42（19）:6609-6619.

[5]West D.Neural network credit scoring models[J].Neural Networks in Business， 2000，27（11）:1131-1152.

[6]Huang C L，Chen M C，Wang C J.Credit scoring with a data mining approach based on support vector machines [J].Expert Systems with Applications，2007，33（4）:847-856.

[7]Lee T S， Chiu C C， Lu C J， et al.Credit scoring using the hybrid neural discriminant technique[J].Expert Systems with Applications， 2002，23（3）:245-254.

[8]Blanco A，Pino-Mejias R，Lara J，Rayo S.Credit scoring models for the microfinance industry using neral networks:Evidence from peru [J].Expert Systems with Applications， 2013，40（1）:356-364.

[9]Aryuni M，Madyatmadja E.Feature selection in credit scoring model for credit card applicant in xyz bank:A comparative study [J].International Journal of Multimedia and Ubiquitous Engineering， 2015，10（5）:17-24.

[10]Florez-Lopez R，Ramon-Jeronimo J.Enhancing accuracy and interpretability of ensemble strategies in credit risk assessment.a correlated-adjusted decision forest proposal[J].Expert Systems with Applications， 2015，42（13）:5737-5753.

[11]Asuncion A，Newman D.UCI machine learning repository[EB/OL].（2008）[2011-02].http://archive.ics.uci.edu/ml

[12]Friedman J H.Greedy Function Approximation:A Gradient Boosting Machine [J].Annals of Statistics，2001，29（5）:1189-1232.

[13]Chang C C，Lin C J.LIBSVM:a library for support vector machines[CP/OL].(2001)[2011-02].http://www.csie.ntu.edu.tw/～cjlin/libsvm.

[14]Fawcett T.An introduction to ROC analysis[J].Pattern Recognition Letters， 2006，27（8）:867-874.

[15]Brown I，Mues C.An experimental comparison of classification algorithms for imbalance credit scoring data sets[J].Expert Systems with Applications， 2012，39（3）:3446-3453.

Personal credit scoring method using gradient boosting decision tree

WANG Li1，2，LIAO Wen-jian2
（1.Wuhan Research Institute of Posts and Telecommunications， Wuhan 430074，China；2.Ltd.Nanjing R&D，FiberHome Communications Science&Technology Development Co.， Nanjing 210019，China）

In recent years，the personal credit scoring problem has become the research hotspots in the credit industry.In view of the current classification algorithms applied in credit scoring only have a good effect for some type of credit data set，a personal credit scoring method based on gradient boosted decision tree （GBDT） methods is put forward in this paper.GBDT is naturally able to deal with mixed types of data sets and find distinguishing features and feature combinations without doing complex feature transformation.GBDT shows obvious advantages for credit data set of complex data types，and by the loss function outliers can be well processed.The contrast experiment based on two UCI public credit audit data sets shows that credit scoring results of GBDT is obviously superior to the result of Support Vector Machine（SVM）and Logistic Regression（LR）with good stability and universal applicability.

credit scoring； classification algorithms； GBDT

TN02

：A

：1674－6236（2017）15-0068-05

2016-07-11稿件编号：201607087

王 黎（1992—），女，湖北宜昌人，硕士。研究方向：数据挖掘。