K-means聚类算法中聚类个数的方法研究
刘 飞,唐雅娟,刘 瑶
(汕头大学 电子工程系,广东 汕头515063)
K-means聚类算法中聚类个数的方法研究
刘 飞,唐雅娟,刘 瑶
(汕头大学 电子工程系,广东 汕头515063)
在数据挖掘算法中,K均值聚类算法是一种比较常见的无监督学习方法,簇间数据对象越相异,簇内数据对象越相似,说明该聚类效果越好。然而,簇个数的选取通常是由有经验的用户预先进行设定的参数。本文提出了一种能够自动确定聚类个数,采用SSE和簇的个数进行度量,提出了一种聚类个数自适应的聚类方法(简称:SKKM)。通过UCI数据和仿真数据对象的实验,对SKKM算法进行了验证,实验结果表明改进的算法可以快速的找到数据对象中聚类个数,提高了算法的性能。
K-means算法;聚类个数;初始聚类中心;数据挖掘;K-means算法改进
近年来,随着科学技术的发展,特别是云计算、物联网等新兴应用的兴起,我们的社会正从信息时代步入数据时代。数据挖掘就是从大量的、不完整的、有噪声的数据中通过数据清洗、数据挖掘、知识表示等过程挖掘出数据隐藏的信息。目前,数据挖掘已经广泛的应用在电信、银行、气象等行业。其中,聚类算法是数据挖掘中比较常见的一种方法,并且广泛的应用在多个领域[1]。K均值算法通常是由有经验的用户对簇个数K进行预先设定,K值设定的不正确将会导致聚类效果不佳[2]。因此,本文提出了一种SKKM聚类算法,可以对K值大小进行确定。
文献[3]中提出了基于划分的聚类算法,该方法对簇的个数并不是自动的获取,而是通过有经验的用户进行设定。现有的自动确定簇个数的聚类方法通常需要给出一些参数,然后再确定簇的个数。如:Iterative Self organizing Data Analysis Techniques Algorithm[4],该方法在实践中需要过多的对参数进行设定,并且很难应用在高维数据中。李永森[5]等人提出将同一个类内部的聚类和不同类之间的距离构建距离代价函数,并且对距离代价函数取值来获得获得最优K值。文献[6]提出了一种非监督的学习方法,通过试探的方法来确定聚类个数,但是该方法实践性不高。文献[7]将K-means方法与基于密度的DBSCAN方法相结合,通过密度准则来选择最佳K值大小。但是为了更快速的确定簇的个数,我们提出了一种可以自动确定聚类个数的聚类方法。
根据SSE[8]度量的性质,我们提出了基于SSE的SKKM聚类算法。该方法通过划分算法来分配数据点的结果,在最终的结果中利用SK来确定最佳聚类个数。即使没有经验的用户,也可以自动确定聚类个数,在实践中更容易使用[9],并且在对UCI中的数据集和仿真数据的实验中证明了SKKM算法的有效性。
1 改进的K-means算法
SKKM算法是本文提出的一种自动确定聚类个数的方法,为了使读者可以更好的了解SKKM算法,我们首先介绍划分聚类方法和SK指标。
1.1 划分聚类方法
K-means算法是将数据集划分为K个簇的方法。簇的个数K是用户自己预先设定,并且簇的中心点是通过簇的质心来进行描述[10-11]。算法在调用的过程中会用到欧式距离和质心的概念[12],现在我们先来看下欧式距离和质心的定义。
定义 1 设向量 ai=(ai1,ai2,…,aim)和bj=(bj1,bj2,…,bjm)分别表示两个数据向量,那么本文说的欧式距离定义为:
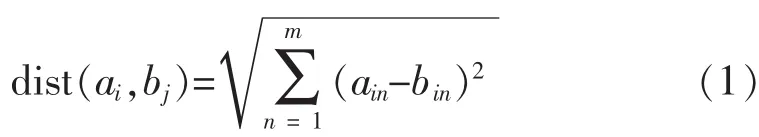
其中n代表该数据集的维数。
定义2对于同一个簇中,该簇的质心定义如下:

其|T|j是该簇的数据个数,Pj为该簇的数据对象。
K-means聚类算法是以K为参数,将数据集N个对象划分为K个数据簇,计算簇的质心,直到准则函数收敛[13]。从而保证簇内数据对象相似度高,簇间数据对象相似度低。
1.2 SK指标
SSE算法是一种用于度量聚类效果的指标。误差平方和越小,表示越接近与它们的质心,聚类效果相应的也就越好。由于SSE是对误差去了平方,因此更加注重远离质心的点。其实有一种有效的方法可以降低SSE的值,但这种方法是增加簇的个数来降低SSE大小,而聚类算法的目标是保持聚类数目在不变的情况下,来提高簇的个数,故该方法并不能有效的保证簇内对象相似,簇间对象相异[14]。而本文提出的SK指标,是将SSE的值和K值相结合,找到相对应的最佳K值,来达到聚类的目的。
定义3 SSE的公式定义如式(3)所示:
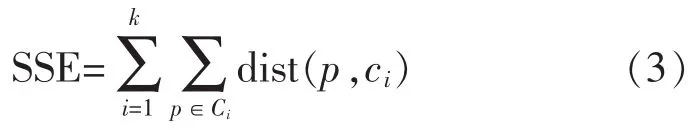
其中Ci表示第i类数据对象的集合。ci是簇Ci的质心,K表示该数据集可以划分为K个簇的集合,dist是欧几里德空间里2个空间对象之间的欧式距离。
定义4 SK的公式定义如式(4)所示:
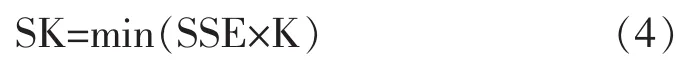
其中,k=2,3,…,10。
通过计算SK的大小,来反推出最佳簇类个数的选取。SK越小,说明聚类效果越好,并且对应的K值即为最佳的簇类个数,而不是通过有经验的用户凭借自己的经验来设置K值大小。因此,一般的用户也可以设置K值大小,从而提高了该算法的性能。
1.3 改进的K-means算法
SKKM算法只能对聚类个数在10个以下的数据对象进行聚类,并且能够自动的确定聚类个数,而不是由有经验的用户进行预先定义。前面已经详细的介绍了划分算法和SK指标的定义,在划分算法的基础上,寻找SK指标的最小值,来确定最佳K值的大小。
1.3.1 算法描述
该算法具体描述如下:
Step1从样本中随机的选择K个数据为初始簇类中心点。且K的取值为2到10的整数值。
Step2通过划分算法对数据对象进行聚类,直到质心大小不再变化。
Step3计算SK的取值。先计算误差平方和,再通过K值的大小来计算SK值。
Step4重复1-3的步骤,直到K取值值遍历完毕。本实验进行100次,求平均SK值大小。
Step5选出最小的SK值,其对应的K值即为最佳聚类个数,输出结果。
1.3.2 算法分析
SKKM算法是在划分聚类算法的基础上,对SK值进行求解,找到相对应的最佳K值。首先随机选择K个点作为初始聚类中心,然后求解各个点到初始聚类中心的距离,选择距离最近的点相对应的簇即为该簇的数据集。重新计算质心,直至质心位置不再发生变化,即数据集归类完毕。我们用误差平方和的大小来评判聚类效果,并使用SK的值来找到最佳K值。在这个过程中,迭代的次数,和数据集误差平方和值的求解是整个程序中主要的开销时间,抽样时间少,使用效率高。
综上,SKKM算法可以以非常小的时间为代价,自动获取聚类个数,提高算法的性能。
2 实验结果与分析
为了验证SKKM聚类算法的性能,本实验使用的是UCI数据库的Iris和Glass数据[15],并且用二维数据集进行仿真实验[16]。UCI数据库是专门用来支持数据挖掘算法和机器学习的常用数据库。仿真数据1和仿真数据2分布于二维的平面上,如图1(a)和图1(c)所示,簇的个数分别为 4个簇和3个簇。因此,K值的选取是衡量该算法优劣的一项重要指标,并且通过UCI数据和仿真数据验证该算法的有效性。这4个数据集分别运行100次,求SK的平均值来找到最佳K值。
图1(a)是仿真数据对象1的二维分布图,通过我们的经验可以将其分为4类,并且用4种不同的形状将其显示出来,如图1(b)。图1(c)是仿真数据对象2的二维分布图,通过我们的经验可以把这些数据对象分为3类,并且用3种不同的形状将其直观的显示出来,如图2(d)。所以K值可以通过有经验的用户进行预先设定,然而高维的数据集并不能进行可视化,如何让机器自己找出最佳K值,是本篇论文的重点,也是难点。为了证明K值能够自动确定最佳聚类个数,我们用表1中的数据进行验证。
2.1 自动确定聚类个数的实验环境
由表1可以看出,Iris是由150个数据集组成的4维数据对象,聚类个数为3。Glass是由214个数据集组成的9维数据对象,聚类个数为6。仿真数据集1是由80个数据集组成的2维数据对象,聚类个数为4。仿真数据集2是由140个数据集组成的2维数据对象,聚类个数为3。这些数据都是在Python中进行实验。接下来,我们用SKKM聚类算法找出最佳K值的大小。
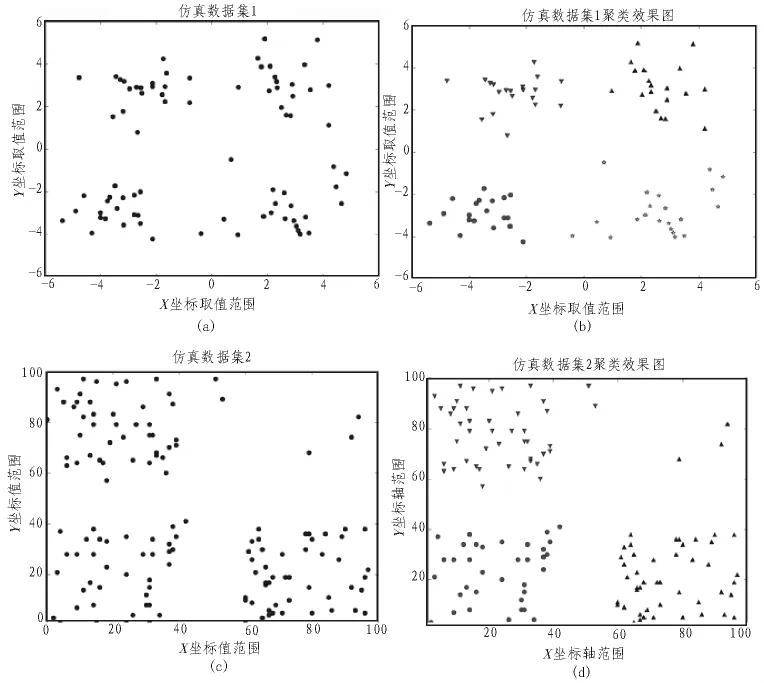
图1 仿真数据分布图
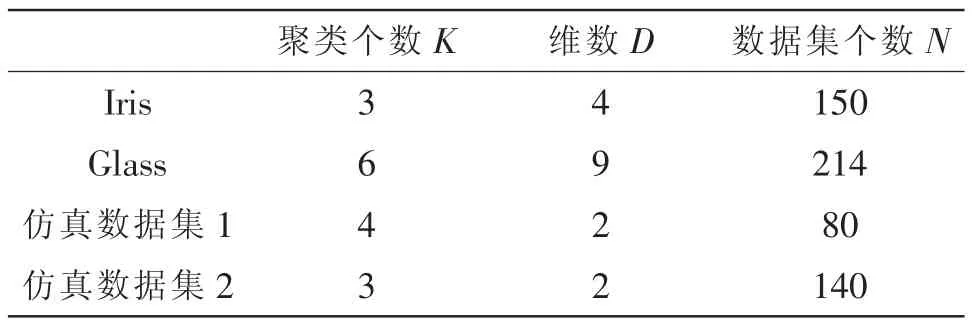
表1 实验数据集信息
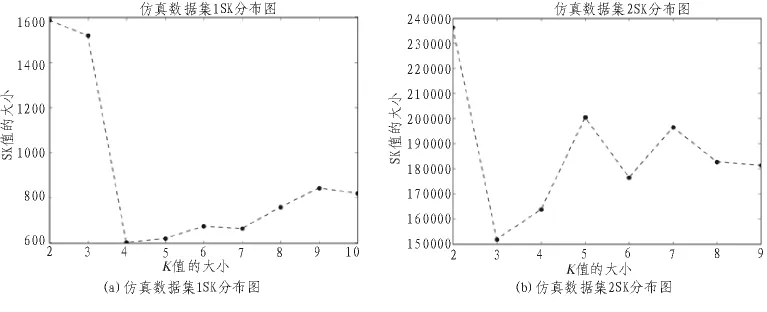
图2 仿真数据分布图
2.2 自动确定聚类个数验证
从表1中我们知道,仿真数据集1和仿真数据集2的数据对象最佳簇点个数分别为4个簇和3个簇。我们用文中提出的SKKM算法找出最佳K值,通过观察仿真数据1的SK分布图图2(a)和仿真数据2的SK分布图图2(b)可以看出,仿真数据集1,其SK最小值相对应K值的大小为4,即4为最佳K值,仿真数据集2,其SK最小值相对应的K值大小为3,即3为最佳K值。所以,我们提出的SKKM算法可以自适应找出最佳K值,与表1中相对应的簇个数相符。但是这些数据集都是二维的数据,现在我们用SKKM算法提到高维中进行实践,找出最佳K值大小。
从表1中我们知道,Iris数据集和Glass数据集的数据对象最佳簇点个数分别为3个簇和6个簇。在这些高位数据集中,通过观察Iris数据集的SK分布图图3(a)可以看出,其最小值SK所对应的K值大小为3,即3为最佳K值。Glass数据集的SK分布图图3(b)可以看出,其最小值SK所对应的K值大小为6,即6为最佳K值。最后,我们通过SKKM算法,找到了Iris数据对象的最佳K值大小为3,Glass数据对象的最佳K值为6。与簇的个数真实值相等,故SKKM算法行之有效。
SKKM算法通过对SK值的选取,找到聚类算法簇的最佳个数,而不是人为的对K值进行设定,与传统的划分K-means算法相比,优化了预先设定K值的缺点,并且通过实验证明了SKKM算法对K值确认的有效性。由此可见,SKKM算法可以有效的解决聚类算法中簇个数选值的问题。但是,SKKM算法在初始中心点的选取问题上,异常点对聚类效果也有一定的影响,不同的初始中心点,最后得出的聚类效果也不一样,本文是在进行100次实验后,最后根据平均值来得出K值大小。
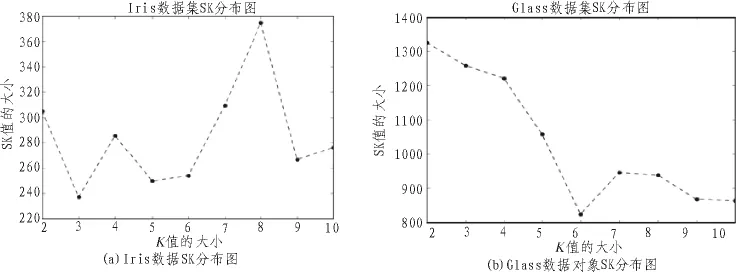
图3 高维数据SSK分布图
3 结束语
在传统的K-means算法中,聚类个数通常是由有经验的用户进行设定,而不是机器自身进行设定。并且聚类算法特有的缺点也会对聚类的效果造成一定的影响。因此,传统算法并不能行之有效的在实践中进行应用。实验表明,文中提出的SKKM算法可以准确的确定聚类个数K的值,而不是人为的进行设定,并且结果也符合预想效果。
[1]郑富兰,吴瑞.基于用户特征的Web会话模式聚类算法[J].计算机应用与软件,2014.
[2]朱烨行,李艳玲,崔梦天,et al.Clustering Algorithm CARDBK Improved from K-means Algorithm[J].计算机科学, 2015,42(3):201-205.
[3]郝洪星,朱玉全,陈耿,等.基于划分和层次的混合动态聚类算法[J].计算机应用研究,2011(1):51-53.
[4]Ma Cai-hong, Dai Qin, Liu Shi-Bin.A Hybrid PSO-ISODATA Algorithm forremotesensing image segmentation[J].Ieee Computer Soc.,2012:1371-1375.
[5]周爱武,陈宝楼,王琰.K-means算法的优化与改进[J].计算机技术与发展,2012(10):101-104.
[6]周涛,陆惠玲.数据挖掘中聚类算法研究进展[J].计算机工程与应用, 2012,48(12):100-111.
[7]王千,王成,冯振元,等.K-means聚类算法研究综述[J].电子设计工程, 2012,20(7):21-24.
[8]LEE S S,Lin J C.An accelerated K-means clustering algorithm selection and erasure rules[J].Zhejiang University -SCIENCE :Computers Electronics,2012,13(10):761-768.
[9]Habib u R M,Liew C S,Wah T Y,et al.Mining personal data using smartphones and wearable devices:a survey[J].Sensors, 2015,15(2):4430-4469.
[10]Tomaev N.Boosting for Vote Learning in High-Dimensional kNN Classification[C]//IEEE International Conference on Data Mining Workshop.IEEE,2014:676-683.
[11]Orakoglu F E, Ekinci C E.Optimization of constitutive parameters of foundation soils K-means clustering analysis[J].Sciences in Cold and Arid Regions,2013,5(5):0626-0636
[12]潘盛辉.移动终端百度地图偏移修正方法的研究[J].信息通信, 2014(10):40-42.
[13]Žalik K R, Žalik B.Validity index for clusters of different sizes and densities[J].Pattern Recognition Letters, 2011,32(2):221-234.
[14]Khan S S,Ahmad A.Cluster center initialization algorithm for K-modes clustering [J].Expert SystemswithApplications, 2013,40(18):7444-7456.
[15]Volker Lohweg.UC Irvine Machine Learning Repository[EB/OL](2012-8).
[16]Wang Y F, Yu Z G, AnhV.Fuzzy C-means method with empirical mode decomposition for clustering microarray data.[J].International Journal of Data Mining&Bioinformatics, 2013,7(2):103-17.
The research method on the clustering number of K-means algorithm
LIU Fei, TANG Ya-juan, LIU Yao
(Department of Electronic Engineering, Shantou University, Shantou 515063, China)
K-means clustering algorithm is a kind of common method of unsupervised learning in data mining.The more different objects are between clusters data,the more similar objects are within cluster data.The phenomenon shows that the cluster effect is better.The selection of cluster number is usually carried out byexperienced users who set parameters.This dissertation proposed a SKKM method in which it determines the number of clusters through adopting SSE and the clustering number.The paper had a verification for SKKM algorithm by UCI data and lots of simulation experiments.The experimental result shows that the improved algorithm can determine the clustering number in the data objects,which achieved a noticeable gain of algorithmic performance.
K-means algorithm; the clustering number; the initial clustering center; data mining;K-means algorithm improvement
TP301
:A
:1674-6236(2017)15-0009-05
2016-08-28稿件编号:201608213
国家自然科学基金面上项目(61471228);广东省重大科技计划项目(2015B020233018)
刘 飞(1990—),男,湖北黄冈人,硕士。研究方向:数据挖掘。

