EM算法在基于区间数据的加速寿命试验统计分析中的应用
邱雷颦
(闽江师范高等专科学校计算机系,福州 350002)
EM算法在基于区间数据的加速寿命试验统计分析中的应用
邱雷颦
(闽江师范高等专科学校计算机系,福州 350002)
在步进加速寿命试验中,当寿命服从广义指数分布且获得的数据是区间数据时,给出试验安排,并通过“各应力下产品失效机理保持不变”等几个基本模型假定,得出各应力水平下形状参数相等的结论以及不同应力水平下的试验时间t1-t0,t2-t1,…,ti-1-ti-2折算到某一应力水平下的时间τi-1的折算公式,进而得出求相关参数的极大似然估计的隐性表达式。进一步讨论利用EM算法求解,先由E步求出期望,再由M步求出使得期望极大化的点,给出具体的迭代过程。最后采用Monte Carlo数据模拟方法分别在大样本和小样本场合下给出了参数真值的估计值,结果表明,该方法在大样本场合下更具有效性。
区间数据;广义指数分布;EM算法
引 言
加速寿命试验,是指将样品置于超过正常应力水平下,通过观察样品的失效时间(即寿命),从而利用统计方法推断在正常应力条件下产品的各项可靠性指标的一种寿命试验。目前常见的类型有恒定应力加速寿命试验,步进应力加速寿命试验,序进应力加速寿命试验。文献[1]中讨论了加速寿命试验的类型和理论基础。本文讨论步进应力加速寿命试验,简称步加试验,是先选定一组加速应力水平S1<… 然而,针对Gupta和Kundu提出的广义指数分布[11],利用EM算法对区间数据的统计分析的研究并不多见。文献[12]指出,在分析很多寿命数据时,广义指数分布往往比其它分布更能有效利用。近年来,双参数广义指数分布已经很广泛的运用到分析寿命数据。文献[13]研究了广义指数分布的尺度参数的极大似然估计基于随机截尾模型。文献[14]介绍了形状参数的增加,使得这一分布族产生了更多的灵活性,使它可以被用来分析删失数据,如区间数据。 本文将主要讨论当获得的寿命数据为区间数据,而寿命分布服从广义指数分布时相关参数的统计分析。 1.1 试验安排 1.2 基本假定 假定1 在应力水平Si(i=1,2,…,m)下,产品的寿命分布为广义指数分布,分布函数为Fi(t)=(1-e-λit)αi,密度函数为fi(t)=αiλi(1-e-λit)αi-1·e-λit,其中λi和αi分别是尺度参数的倒数和形状参数,和应力水平Si有关。 假定2 在应力水平Si(i=1,2,…,m)下,产品的失效机理保持不变[1]。 假定3 产品在应力水平S下,满足线性加速模型lnλi=a+bφ(Si),其中φ(Si)是与应力水平Si有关的已知函数,下记φi,i=1,2,…,m。 假定4 产品的剩余寿命仅依赖于当时已累积失效的部分和当时的应力水平,而与累积的方式无关[15]。 引理1 在应力水平Si(i=1,2,…,m)下,产品的寿命分布为Fi(t)=(1-e-λit)αi,则αi≡α(i=1,2,…,m)。 由基本假定2,在应力水平Si(i=1,2,…,m)下,产品的失效机理保持不变,即加速系数是与R无关的常数,因此要求αi≡α(i=1,2,…,m)。 引理2 若记τi-1为产品经历了水平S1,S2,…,Si-1的步加试验后,各段试验延续时间t1-t0,t2-t1,…,ti-1-ti-2折算到Si应力水平下总的折算时间,则 证明 由基本假定4知τi-1满足 又由假定1和假定2得: (1-e-λiτi-1)α=(1-e-λi-1(ti-1-ti-2+τi-2))α 得到, e-λiτi-1=e-λi-1(ti-1-ti-2+τi-2) 由此得到递推公式 又由τ0=0得 其中,i=2,3,…,m。由基本假定知, 所以,τi-1为b的函数,下记τi-1(b), i=1,2,…,m。 估计a,b,α三个参数。记n个样品的失效时间为Xk,k=1,2,…,n,它们是独立同分布的随机变量,密度函数为f(x)=αλ(1-e-λx)α-1·e-λx, x>0,λ>0,α>0。只能观测到落在区间[ti,ti+1)中的样本数ni,其中i=0,1,2,…,m,0=t0 x落在区间[ti,ti+1)中的概率为 P(x∈[ti,ti+1))=Fi+1(ti+1)-Fi(ti)= [1-e-λi+1(ti+1-ti+τi(b))]α-[1-e-λi(ti-ti-1+τi-1(b))]α 其中记t-1=τ-1(b)=0,λ0=λm+1=0。 定理1 参数a,b,α的极大似然估计可以由隐性表达式求解。 (1) (2) (3) 其中, 证明 容易得到似然函数为 对数似然函数为 式(1)、式(2)和式(3)无法得出a,b,α的显性表达式,于是考虑用EM算法实现。 为了便于表述,n个样品的失效时间Xk,k=1,2,…,n的全体记为X,观测结果即落在区间[ti,ti+1)中的样本数目ni, i=0,1,2,…,m, 0=t0 于是 [1-exp[-ea(k)+b(k)φi(t-ti-1+τi-1(b(k)))]]α(k)-1· exp[-ea(k)+b(k)φi(t-ti-1+τi-1(b(k)))] 其中, [1-exp[-ea(k)+b(k)φi(ti-ti-1+τi-1(b(k)))]]α(k)- [1-exp[-ea(k)+b(k)φiτi-1(b(k))]]α(k) 所以 其中, AiAi(a,b,t)1-exp[-ea+bφi(t-ti-1+ τi-1(b))] (4) a= (5) (6) 迭代过程: (1)当k=0时,给定参数初始值a(0),b(0),α(0),及任意小的正数ε。 (2)当k≥1时,现有的参数估计为a(k),b(k),α(k)。 ①取式(4)右边的,b=b(k),即可找到α(k+1), ②取式(5)右边的b=b(k),a=a(k),α=α(k),即可找到a(k+1), ③令式(6)为零,即可解出b的显示表达式,令表达式中a=a(k),b=b(k),α=α(k)找到b(k+1), 其中, (t-ti-1+τi-1(b(k)))] 满足迭代终止的条件后继续进行20次迭代,取所得到的20个参数迭代值的平均值作为对真实参数的估计 考虑步进加速寿命试验过程中的应力为温度,其中T1=240,T2=350,T3=470,φi=φ(Ti)=1/Ti,t0=0,t1=1.20×104,t2=1.55×104,t3=1.66×104,参数真值为a=-20,b=104,α=2,取迭代初始值a(0)=-18,b(0)=12000,α(0)=2.5。 在小样本场合下,取n0=n1=n2=5,ε=10-3,在大样本的场合下,取n0=n1=n2=100,ε=10-3运用以上迭代过程得到参数真值的估计,见表1。 表1 模拟结果 由数据模拟结果表1可知,在大样本场合下,估计值与参数真值的相对误差有所减小。因此,在产品寿命服从广义指数分布的情况下,基于获得的数据为区间数据的步进加速寿命试验,在大样本场合下利用EM算法给出参数的最大似然估计显得更为有效。 [1] YANG Y H,ZHOU Y Q.Theoretical foundation of accelerated life testing[J].Journal of Propulsion and Technology,2001,22(5):353-356. [2] ZHAO W,ELSAYED E A.A general accelerated life model for step-stress testing[J].IIE Trans,2005,37:1059-1069. [3] MOHAMED T.Step-Stress Accelerated Life Tests[C]//Miodrag Lovric.International Encyclopedia of Statistical Science,Springer,America:2011:1547-1517. [4] DEMPSTER A P,LAIRD N M,RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm[J].Math SciNet Google Scholar.JR Stat Soc Ser B,1977,39:1-22. [5] WU C F.On the convergence properties of the EM algorithm[J].The Annals of Statistics,1983,11(1):95-103. [6] AMBROISE C.The EM Algorithm and Extensions[J].Journal of classification,1988,15(1):154-156. [7] CHARLES B,PAUL P B.Handbook of Mathematical Methods in Imaging[M].New York:Springer-Verlag,2015. [8] HUANG W H,CHEN Y G.The multiset EM algorithm[J].Statistics & Probability Letters,2017,126:41-48. [9] SUVRA P,BALAKRISHNAN N.Destructive negative binomial cure rate model and EM-based likelihood inference under Weibull lifetime[J].Statistics & Probability Letters,2016,116:9-20. [10] JEAN-PATRICK B,GILLES C.EM for mixtures[J].Statistics and Computing,2015,25(4):713-726. [11] GUPTA R D,KUNDU D.Generalized exponential distributions[J].Australian & New Zealand Journal of Statistics,1999,41:173-188. [12] CHIANG-SHENG L,HSINE-JEN T.A note on the generalized linear exponential distribution[J].Statistics & Probability Letters,2017,124(5):49-54. [13] NAMHYUN K.Approximate MLE for the scale parameter of the generalized exponential distribution under random censoring[J].Journal of the Korean Statistical Society,2014,43(1):119-131. [14] DEBASIS K,RAMESHWAR D G.An extension of the generalized exponential distribution[J].Statistical Methodology,2011,8(6):485-496. [15] NELSON W B.Accelerated life testing-step-stress models and data analysis[J].IEEE Transaction on Reliability,1980,29(2):103-108. Statistical Analysis Based on EM Algorithm for Accelerated Life Testing Under Interval Censored Samples QIULeipin (Department of Computer Science, Minjiang Teachers College, Fuzhou 350002, China) An accelerated life test carried out by step stress is considered when the the life time follows a generalized exponential distribution and the failure data obtained is interval censored. The test procedure is presented and the exchange formula of time is given by some assumptions. With the help of the expectation-maximization (EM) algorithm which is widely used when the observations can be viewed as incomplete data, the maximum likelihood estimates are computed. Moreover, an example by Mote Carlo data simulation is given to illustrate the procedure and show that this method is available, especially in large sample case. interval censored; generalized exponential distribution; EM algorithm 2017-06-06 福建省教育厅中青年课题(JAT160827) 邱雷颦(1980-),女,福建石狮人,讲师,硕士,主要从事概率与数理统计方面的研究,(E-mail)qiuleipin@163.com 1673-1549(2017)04-0081-06 10.11863/j.suse.2017.04.15 0212.7 A
1 试验安排及基本模型假定

2 参数估计


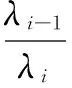
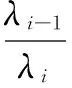


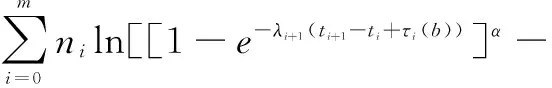
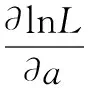
3 EM算法求极大似然估计
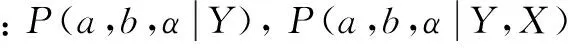
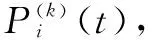











4 数据模拟


