YALMIP工具箱在运筹学实验教学中的应用
俞武扬
( 杭州电子科技大学 管理学院,杭州 310018)
YALMIP工具箱在运筹学实验教学中的应用
俞武扬
( 杭州电子科技大学 管理学院,杭州 310018)

Matlab平台对于运筹学中各种经典优化模型的实验教学具有重要作用,然而由于Matlab工具箱中函数的调用格式限制条件非常严格,从而导致将实验数据表示成Matlab所需矩阵形式时容易造成实验教学效率低下的情况。借助于YALMIP工具箱结合Matlab软件实现了运筹学实验教学中经典模型的求解,对线性规划、运输问题、背包问题、最短路问题等等结合具体例子说明了YALMIP语言的建模方法。利用YALMIP的统一建模语言,很容易对各种运筹学典型问题的模型加以实现,从而降低了利用软件解决模型问题的难度,同时也对解决运筹学实验中的其它问题有借鉴作用。
运筹学; 实验教学; Matlab; YALMIP工具箱
0 引 言
线性规划、运输问题、整数规划以及图论中的最小树、最短路、最大流等问题都是运筹学中的经典问题[1-5],在运筹学教学特别是运筹学实验中需要学生掌握这些经典问题的软件求解[6-8]。目前国内高校在运筹学实验中最常见的工具主要有Excel、WinQSB、Matlab和Lingo软件。其中Excel功能相对比较简单,适用于小型问题的求解演示[9]。WinQSB主要是采用模块化的程序进行演示,可扩展性较差且在国内应用相对较少[10]。Matlab软件功能非常强大,对于一些工科类学科而言具有不可替代的地位,然而在运筹学教学过程中由于Matlab软件对于输入约束条件都要求采用矩阵乘积形式,这对于一般形式的优化模型造成了不小的转换困难[11-12]。而Lingo软件在功能方面比较单一,对于优化结果的图形化显示方面不如Matlab强大[13-14]。本文介绍在Matlab软件平台上开发的用于求解最优化问题的Yalmip工具箱,它不仅可以利用Matlab强大的计算能力,调用Matlab中各种工具箱中的函数,而且对其他优化求解器(如Cplex和Gurobi等)提供了一种统一的建模调用方案。
利用YALMIP工具箱结合Matlab软件建立相应的模型在运筹学实验教学过程中是一种新的尝试。本文阐述了利用Yalmip工具箱求解运筹学经典问题的方法,并结合实例说明了Yalmip工具箱在运筹学实验教学中的具体应用。
1 YALMIP简介
YALMIP是Lofberg开发的一个免费Matlab工具箱,它提供了关于凸优化与非凸优化问题的一种高级建模求解语言。YALMIP不但包含基本的线性规划求解算法,如linprog(线性规划)、bintprog(二值线性规划)、bnb(分支定界算法)等,它还提供了对Cplex、Gurobi、Glpk、Lpsolve等求解工具箱的包装。通常,不同的求解器对于优化问题的描述并不一致,在使用时需要较多的学习成本并且容易出错。而Yalmip真正实现了建模和算法二者的分离,提供了一种简单而统一的建模语言和编程接口,以实现不同求解器之间的集成。因此,我们只需要知道在Matlab下如何用Yalmip的方式建模,而不需要针对每一种工具箱学习新的建模语法。
Yalmip工具箱可以通过下载网址http://users.isy.liu.se/johanl/yalmip/pmwiki.php?n=Tutorials.Installation获得。下载安装包并解压后,通过如下步骤在Matlab软件中设置引用路径:① 点击File中的Set Path菜单;② 点击Add with subfolders菜单,找到解压好的文件夹Yalmip;③ 点击确定、保存。对于外部的求解器,可采用类似方式设置Matlab路径。
Yalmip的建模语法简单到只有四个最基本的命令:
(1) 创建决策变量。
>>x=sdpvar(m,n,[option]): 创建m*n的连续型决策变量矩阵,option是对矩阵的一些参数指定;
>>x=intvar(m,n,[option]): 创建m*n的整数型决策变量矩阵;
>>x=binvar(m,n,[option]): 创建m*n的0-1型决策变量矩阵。
注:若决策变量x是n*n的方阵,如果没有对决策变量进行参数指定,则默认x为对称矩阵,否则需要加以参数指定,即以x=sdpvar(n,n,’full’)的形式定义,整数型与0-1型类似。
(2) 约束条件设置。
>>F=set(constraint,[tag]): 创建一个以constraint指定的约束,可选参数tag可以给该约束指定一个字符串标记。其中constraint的表示极为自然,例如有x1+x2+x3<=10的约束,直接写成:
>>x=sdpvar(3,1);
>>F=set(x(1)+x(2)+x(3)<=10);
如果要添加多个约束可以直接用+连接:
>>F=set(constraint1,[tag1])+set(constraint2,[tag2])。
(3) 参数配置。
>>ops=sdpsettings(option1,value1,option2,value2,…);
例如:>>ops=sdpsettings(‘solver’,’Cplex’,verbose’,2);
参数‘solver’指定程序用Cplex求解器(必须已安装,否则报错),如果不指定’solver’参数,Yalmip会根据决策变量类型自动选择最适合的求解器;’verbose’指定显示冗余度(冗余度越大,求解过程信息越详细)。
(4) 求解。
>>result=solvesdp(F,f,ops); 求解一个最小化数学规划问题,该问题的目标函数由f指定,约束由F指定,ops指定求解参数,最后的结果则存储在result结构体中,可用double命令显示。
>>x_star=double(x);
>>f_star=double(f);
2 线性规划问题
线性规划是运筹学中最重要的一个分支,几乎所有的优化求解器都可以求解线性规划问题,下面先给出线性规划问题的数学模型:
minZ=CX
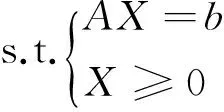
例1 minZ=12x1+5x2+8x3

与该线性规划问题相对应的Yalmip程序为:
C=[12 5 8];
A=[2 3 1;4 1 5];
b=[30; 15];
x=sdpvar(3,1);
f=C*x;
F=set(A*x>=b)+set(x>=0);
result=solvesdp(F,f);
x_star=double(x)
f_star=double(f)
求得结果为:最优解x_star=[0;9.6429;1.0714],最优目标函数值为f_star=56.7857。
3 运输问题
运输问题模型是运筹学中的经典模型之一,运输问题的一般描述如下:某种物资有m个产地和n个销地,产地i到销地j的单位物资运输费用为cij,各个产地的产量分别为ai,各个销地的销量分别为bj,要求在满足产销约束条件下使总运输费用最少的运输方案。
例2 现有4个产地,5个销地,其中cij、ai、bj见表1,求该运输问题的解。
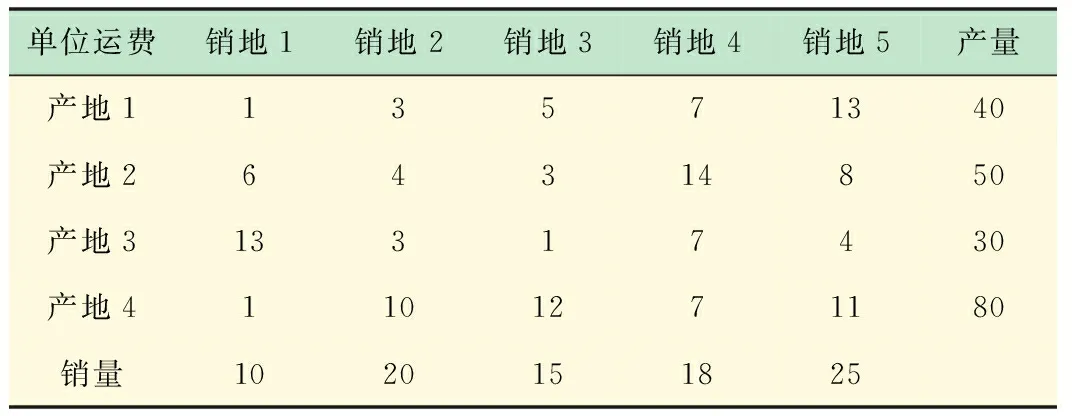
表1 运输参数表
相应的Yalmip程序为:
C=[1 3 5 7 13; 6 4 3 14 8; 13 3 1 7 4; 1 10 12 7 11];
a_i=[40;50;30;80];
b_j=[10;20;15;18;25];
x=sdpvar(4,5,'full');
f=sum(sum(C.*x));
F=set(sum(x,2)<=a_i)+set(sum(x,1)>=b_j')+
set(x>=0); %sum(x,2)表示关于矩阵x按行求和,
%sum(x,1)表示关于矩阵x按列求和。
result=solvesdp(F,f);
x_star=double(x)
f_star=double(f)
求得结果为:

4 背包问题
背包问题是一类重要的整数规划模型,其一般描述如下:设背包的载重量和容积分别为W和V,第i种物品的重量、体积和数量分别为wi、vi和ci,该种物品的效用为ei,在背包载重量和容积限制条件下,使得背包装载物品总效用最大化。
例3 有10种物品的质量wi、体积Vi、数量ci以及效用ei见表2所示,背包载重量为80,容积为60,求背包装载物品总效用最大化的方案。

表2 物品属性表
相应的Yalmip程序为:
wi=[17,19,3,19,13,2,6,11,20,20];
Vi=[2,10,10,5,9,2,5,10,8,10];
ci=[5,2,4,3,5,4,3,1,5,3];
ei=[8,1,11,12,9,10,9,5,8,3];
W=80;
V=60;
x=intvar(10,1,'full');
f=ei*x;
F=set(wi*x<=W)+set(Vi*x<=V)+
set(0<=x’<=ci);
result=solvesdp(F,-f); %最大化目标函数
x_star=double(x’)
f_star=double(f)
求得结果为:
x_star=[1 0 3 1 0 4 3 0 0 0],f_star=120。
5 指派问题
指派问题也是一类重要的整数规划问题,其一般描述如下:现要安排n个人去完成n项不同的工作,第i个人完成第j项工作所需时间为cij,要求每人完成一项工作,每项工作只由一人完成,求使得完成所有工作总时间最少的指派方案。
例4 现有5人完成5项工作所需时间如表3所示,要求每人只做一项工作,每项工作只由一人完成且所用总时间最少的指派方案。
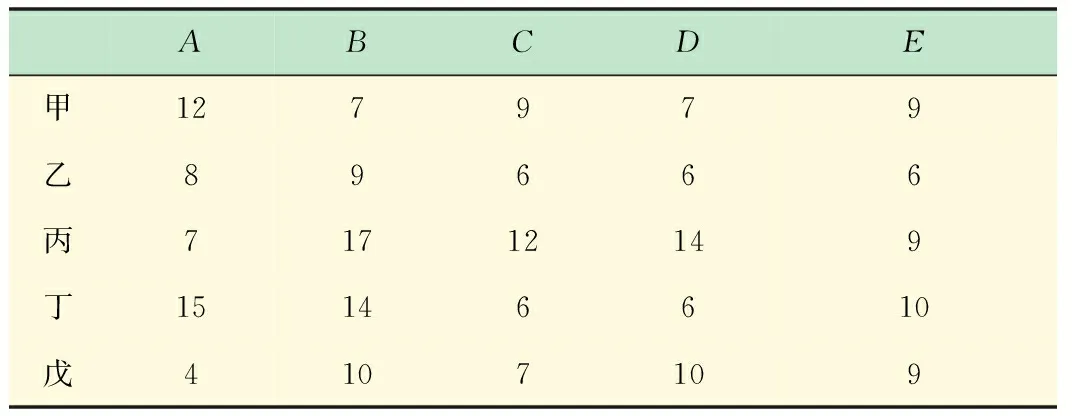
表3 时间效率表
相应的Yalmip程序为:
cij=[12 7 9 7 9;8 9 6 6 6;7 17 12 14 9;15 14 6 6 10; 4 10 7 10 9];
xij=binvar(5,5,'full');
f=sum(sum(cij.*xij));
F=set(sum(xij,1)==1)+set(sum(xij,2)==1);
result=solvesdp(F,f);
x_star=double(xij)
f_star=double(f)
求得结果为:

6 最短路问题
最短路问题的一般提法如下:设G=(V,E)为连通图,图中各边[vi,vj]有权lij(lij=∞表示vi,vj不相邻),vs,vt为图中任意两点,设μ是G中从vs到vt的一条路定义路μ的权为μ中所有边的权之和,记为ω(μ)。最短路问题就是要从所有从vs到vt的道路中,求一条从vs到vt的所有道路中总权最小的道路μ0,即
例5 设有一批货物要从V1运到V7,网络图见图1,边上的数字表示该路距离,求最短距离的运输路线。
相应的Yalmip程序为:
C=[0 1 4 100 100 100 100; 1 0 2 4 2 5 100; 4 2 0 100 100 1 100; 100 4 100 0 2 100 100; 100 2 1 2 0 3 2; 100 5 1 100 3 0 6; 100 100 100 100 2 6 0];
x=binvar(7,7,’full’);
F=set(sum(x(1,:)-sum(x(:,1))==1)+set(sum(x(7,:))-sum(x(:,7))==-1);
fori=2:6
F=F+set(sum(x(i,:))-sum(x(:,i))==0);
end
f=sum(sum(C.*x));
result=solvesdp(F,f);
x_star=double(x)
f_star=double(f)
结果为:x(1,2)=1,x(2,5)=1,x(5,7)=1;相应的最短路线为V1→V2→V5→V7,最短距离为5。
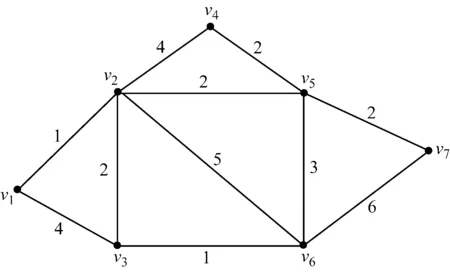
图1 非线性状态观测器框图
7 最大流问题
设有向图G=(V,E),G的每一条边(vi,vj)上的非负数cij称为边的容量,仅有一个入次为0的点vs称为发点(源),一个出次为0的点vt称为收点(汇),其余的点为中间点,这样的网络G称为容量网络,记作:G=(V,E,C)。当每条边上的实际流量小于等于其容量时,流动才能顺利进行。对于给定的容量网络,如何求出从发点到收点的最大可行流量就是最大流问题。
例6 假设某山区有6个村庄。村庄与村庄之间虽有公路,但是通行的能力有很大差异,边上的数字小则表示通行能力差,反之则表示通行能力强(见图2)。试求出从村庄1~6之间的最大流。

图2
相应的Yalmip程序为:
C=[0 4 0 0 6 0;0 0 4 4 1 0;0 0 0 2 2 0;0 0 0 0 0 9;0 0 0 6 0 7;0 0 0 0 0 0];
x=intvar(6,6,'full');
F=set(sum(x(:,1))==0)+set(sum(x(6,:))==0)+set(0<=x<=C);
fori=2:5
F=F+set(sum(x(i,:))-sum(x(:,i))==0);
end
f=sum(x(s,:));
result=solvesdp(F,-f);
f_star=double(f)
x_star=double(x)
结果为:

8 最小费用最大流问题
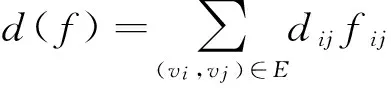
例7 假设从仓库V4到商店V5要运送8个流量的货物,边上左边数字表示线段最大通过能力,右边数字表示通过单位流量的费用(见图3),试求出费用最小的运输方案。

图3
相应的Yalmip程序为:
C=[0 0 2 0 7;5 0 10 0 0;0 0 0 0 4;10 8 0 0 0;0 0 0 0 0];
D=[0 0 6 0 1;2 0 3 0 0;0 0 0 0 2;4 1 0 0 0;0 0 0 0 0];
x=intvar(5,5,'full');
F=set(sum(x(:,4))==0)+set(sum(x(5,:))==0)+set(0<=x<=C)+set(sum(x(4,:))==8);
fori=1:3
F=F+set(sum(x(i,:))-sum(x(:,i))==0);
end
f=sum(sum(D.*x));
result=solvesdp(F,f);
f_star=double(f)
x_star=double(x)
结果为:

9 结 语
在运筹学教学过程中结合实验教学要求,利用YALMIP工具箱在Matlab环境中求解问题是一种新的尝试。由于YALMIP工具箱提供了一种简洁而统一的建模语法,比Matlab原有语言的表达方法更为易于掌握,可使学生更为关注问题建模的本质,而不需要在求解函数的区别上分散注意力,因此从运筹学实验教学的角度来看,结合YALMIP与Matlab以用于求解运筹学模型值得进一步的推广。
[1] 韩大卫. 管理运筹学[M].6版,大连:大连理工大学出版社,2010.
[2] 胡运权,郭耀煌. 运筹学教程[M].4版,北京:清华大学出版社,2012.
[3] 弗雷德里克.S.希利尔. 运筹学导论[M].10版,北京:清华大学出版社,2015.
[4] 韩伯棠. 管理运筹学[M].4版,北京:高等教育出版社,2015.
[5] 卜心怡,俞武扬,余福茂,等.管理运筹学[M].北京:电子工业出版社,2016.
[6] 夏良玉.案例教学和上机实验一体化的运筹学教学模式探讨[J].科教导刊,2013(14):113-115.
[7] 赵清俊,陈桂兰.运筹学实验软件在线性规划问题教学中的应用[J].重庆文理学院学报,2013,32(3):110-112.
[8] 邓胜岳,周立前,方四林,等.数学建模和数学实验在《运筹学》课程教学中的应用研究[J].湖南理工学院学报(自然科学版),2015,28(1):91-94.
[9] 于瑛英.EXCEL运筹学规划论教学中的应用[J].教育教学论坛,2014(10):278-280.
[10] 邓 萍,吕俊娜,闫 芳,等.基于QSB软件的运筹学实验教学研究[J].课程教育研究(学法教法研究),2015(34):21-21.
[11] 杨毓玲.基于Matlab的运筹学实验教学研究[J].科技经济市场,2012(11):115-116.
[12] 张 明,王文文.Matlab在经管类运筹学教学中的探索与实践[J].大学教育,2012,7(1):81-83.
[13] 谢金星,薛 毅. 优化建模与LindoLingo软件[M].北京:清华大学出版社,2005.
[14] 洪 文,朱云鹃,金 震,等. Lingo在运筹学实验教学中的应用[J]. 实验室研究与探索,2012,31(4):265-270.
Application of YALMIP in Experiment Teaching of Operations Research
YU Wuyang
(Management School, Hangzhou Dianzi University, Hangzhou 310018, China)
Matlab platform plays an important role in operations research experiment teaching for all kinds of classical optimization models. Since many functions within Matlab toolboxes have very strict format constraints, which result in the poor efficiency of experiment teaching when we represent experimental data into the matrix form of Matlab. Combining the YALMIP toolbox with Matlab can solve the classic models in operations research, such as linear programming, transportation problem, knapsack problem, the most short circuit problem, and so on. Concrete examples are given to illustrate the modeling method of YALMIP language. Using unified modeling language of YALMIP, it is easy to implement these classical optimization models of operations research. The method reduces the difficulty of solving the problem of models by software, and this toolbox can also be used to solve other problems in operations research experiment.
ooperations research; experiment teaching; Matlab; YALMIP toolbox
2016-11-22
杭州电子科技大学“管理科学与工程”重点研究基地项目(ZD06-201601)
俞武扬(1974-),男,浙江嵊州人,博士,副教授,研究方向:物流建模与优化计算。
Tel.:0571-86878533;E-mail:yu_wuyang@163.com
O 221.6
A
1006-7167(2017)08-0274-05

