基于改进差分进化算法的水火电短期优化调度
黄 迪,徐 刚,向红艳,李英海
(1.湖北清江水电开发有限责任公司,湖北宜昌443000;2.三峡大学水利与环境学院,湖北宜昌443002;3.水资源安全保障湖北省协同创新中心,湖北武汉430072)
基于改进差分进化算法的水火电短期优化调度
黄 迪1,徐 刚2,3,向红艳1,李英海2
(1.湖北清江水电开发有限责任公司,湖北宜昌443000;2.三峡大学水利与环境学院,湖北宜昌443002;3.水资源安全保障湖北省协同创新中心,湖北武汉430072)
在处理具有复杂约束条件的水火电系统短期优化调度问题时,针对差分进化算法(DE)变异率控制难点和“早熟”问题,引入自适应变异算子,以距离方差校验,借正态分布生成种群,提出改进差分进化算法(EDE)。为使可行解在约束范围内收敛,运用双适应度函数对求解过程评价。以国际上通用4个水电站和3个火电站组成的系统仿真分析,EDE使水火电总燃料费用最小,为水火电力系统求解提供了有效手段。
改进差分进化算法;梯级水电站;联合优化调度;水火电系统
0 引 言
水火电系统是由梯级水电站群和若干个火电站组成的电力系统,其联合优化调度是一个具有复杂约束的大型、动态、有时滞的决策问题,处理起来比较复杂[1]。为了节能减排,同时使水火电系统效益最大化,需要在满足水火电系统各种约束条件下,使火电燃料费用最小,水能利用率最大。水火电联合优化调度模型的求解方法,常见的有动态规划法[2]、拉格朗日松弛法[3]、神经网络法[4]、遗传算法[5]、模糊决策法[6]和粒子群算法[7]。差分进化算法(DE)在求解该类问题时,控制参数少,收敛速度快,有较强的全局搜索能力。
目前,DE算法的研究主要集中在对操作算子的改进和算法的集成研究两大领域[2]。针对水火电系统联合优化调度这种高维度多目标问题,DE算法存在早熟[9-10]和停滞[11]现象。本文尝试引入自适应变异算子,利用正态分布重新生成个体对DE算法集成,并做定量分析,提出改进差分进化算法(EDE)。针对水火电系统复杂的约束条件,本文引入双适应度函数,加入放大系数进行改进,将数学模型构造成一个双目标、多约束的问题。通过实例应用,希望使EDE适用于求解水火电力系统短期优化调度这类具有复杂约束条件的问题。
1 改进差分进化算法
DE算法是一种并行直接搜索方法,包括初始化、变异、交叉、选择。文献[12]对DE算法作了详细的介绍。下面就DE存在的问题给出改进措施。
1.1 DE算法存在的早熟和停滞问题
DE是根据父代个体间的差分矢量进行变异,交叉和选择,与遗传算法很类似,也存在着易陷于局部最优过早收敛的现象[9-10],即早熟。文献[11]结合参数优化问题给出了DE停滞现象的简单例子。算法停滞后,种群不会收敛,仍然保持了多样性,但不会产生新个体,因此不同于早熟。
1.2 针对早熟的改进
针对早熟问题,本文采用自适应变异算子,根据算法进展程度自适应修改变异率,在初期有较大变异率,在后期趋于稳定。变异算子设计如下:
F=F0·4(1-G/Gmax)
(1)
式中,F0为变异参数;Gmax为最大进化代数;G为当前的进化代数。
为了判断进化过程中,算法是否早熟,参照文献[13]给出距离方差的定义

(2)
式中,xi,j为第i个个体第j维的值;xj,avg为种群中所有个体第j维优化变量的平均值;δj为第j维优化变量的距离方差。当δj小于给定的值ε时可判定算法出现早熟现象。
1.3 针对停滞的改进
借鉴文献[11]的思想,本文在最优解附近生成新的种群,以有效解决算法停滞的问题。当判断出算法停滞后,更新当前的种群中的个体,其方法为:首先计算出当前种群个体的上限u和下限l,在这个范围内随机生成新个体,这样可以有效的缩小搜索范围,个体数量占种群大小百分比为p(其取值一般为50%~80%),然后在当前停滞的种群中选择最优个体a,重新在最优个体周围按正态分布生成新个体,即
(3)

按正态分布在最优个体周围产生的个体数取1-p,用两种方法产生的全部个体来替代当前种群。这样产生的个体在可行解内不但具有多样性而且还有一部分个体分布在当前的最优个体附近,利于算法收敛并可以有效解决停滞现象。
1.4 改进差分进化算法(EDE)
采用EDE算法求解水火电系统短期优化调度的步骤如图1所示。
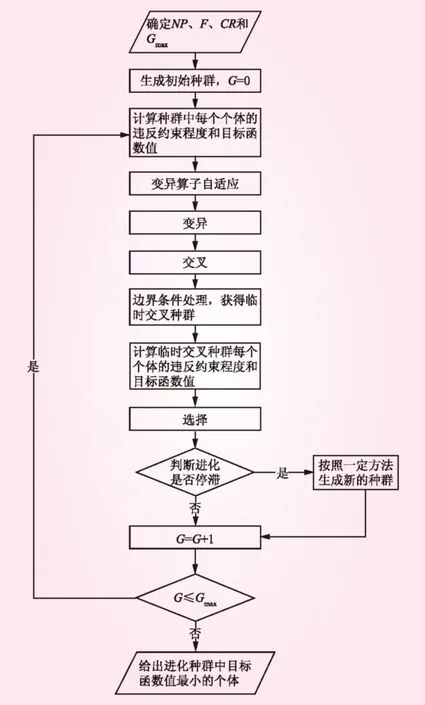
图1 EDE算法流程
2 基于EDE的水火电系统短期优化调度研究
本文以国际上广泛采用的由4个级联水电站和3个火电站组成的水火电力系统为实例对象[14-15],以EDE算法作为解算方法,探求水火电系统短期优化调度的有效求解方法。其中,梯级水电站结构及水流时滞情况见图2。

图2 梯级水电站连接关系
2.1 编码方式及初始种群的生成
将所有水电站的时段末库容和Ns-1(Ns为系统中火电站个数)个火电站时段出力按时间和如下水、火电站编号顺序连接起来作为种群中的个体。即
(4)
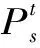
种群中的个体可按式(5)和式(6)初始化。即
(5)
(6)
式中,rand()为[0,1]内均匀分布的随机数。
2.2 约束条件的处理
水火电联合优化调度问题的约束条件较为复杂,负荷火电站确保系统负荷平衡约束得到满足。即,假定用作负荷平衡的火电站索引为k,则令其时段出力
(7)

为了保证可行解在约束范围内收敛,本研究借鉴文献[16]提出的双适应度函数思想,以个体目标函数值(总发电费用)F作为主适应度,构造个体违反约束条件相对程度F1作为副适应度[17],并添加放大系数加以改进,以加快寻找可行域的速度。改进后的个体违反约束条件相对程度
(8)

(9)
式中,αm和βm均为放大系数;m=1,2,3。
经过上述变换,若F1=0,则表明该个体完全满足约束条件,为可行解;若F1>0,则该个体为不可行解,F1越大,违反约束程度越大。可按照以下两条规则比较个体间的优劣,指导进化:①若F1不相等,则F1较小的个体相对更优;②若F1相等,则F较小的个体相对更优。
3 实例分析
已知某一天24 h电力系统负荷过程及水库上游来水过程[14-15]如表1和表2所示。采用EDE算法对系统最优出力分配过程进行求解,计算时段间隔为1 h。以出力范围最大的火电站作为负荷平衡电站。有关各水、火电站的相关参数及约束条件来源于文献[14-15]。设置EDE算法的种群规模NP=400,最大进化代数Gmax=2 000。初始变异算子F=1.0,交叉算子CR=0.4。式(9)中的几个放大系数设置如下:α1=1,β1=2λ,α2=0.5λ,β2=1.5λ,α3=0.5λ,β3=1,其中λ=14。

表1 电力系统负荷

表2 水库上游来水过程

表3 水火电系统短期优化调度结果 MW
考虑到算法优化过程的随机性,采用EDE算法独立运算20次,取其中的最优解作为计算结果。经过多次计算,得到火电站总燃料费用最小值为43 597$,各水电站弃水量均为0。表3为水火电系统的时段出力分配过程,图3为其出力叠加,负荷分配结果完全满足各水、火电站出力约束条件及系统负荷平衡条件。

图3 水火电站出力叠加效果
图4为优化计算中火电站总燃料费用F和违反约束程度F1的收敛曲线。

图4 双适应度收敛曲线
由图4可知,随着违反约束程度的降低,火电站费用急剧下降。由此可见:采用双适应度函数约束处理方法的EDE求解算法在处理具有复杂约束条件的水火电系统短期优化调度问题时,表现出良好的收敛性能和约束处理能力。
将EDE计算结果同进化规划法(EP)、模拟退火算法(SA)粒子群算法(PSO)和差分进化算法(DE)进行对照(见表4)。其中,EP、SA及PSO计算结果引自文献[16]。由表4可见,EDE算法在求解水火电系统短期优化调度问题上表现出良好的寻优能力。

表4 不同智能算法优化结果对比
4 结 语
本文提出改进差分进化算法(EDE)运用于水火电系统短期优化调度研究。针对研究对象复杂的约束条件,将水火电站顺序连接编码,设一负荷平衡电站求解。计算结果表明,与DE算法相比,EDE兼顾求解精度和搜索效率,为求解水火电系统联合优化调度提供了新思路。
[1]张勇传. 水电站经济运行原理[M]. 北京: 中国水利水电出版社, 1998.
[2]SHAWWASH Z K, SIU T K, RUSSELL S O D. The B.C. hydro short term scheduling optimization model[J]. IEEE Transactions on Power Systems, 2000, 15(3): 1125- 1131.
[3]NARESH R, SHARMA J. Hydro system scheduling using ANN approach[J]. IEEE Transactions on Powers Systems, 2000, 15(1): 388- 394.
[4]ORERO S, IRVING M. A genetic algorithm modeling framework and solution technique for short term optimal hydrothermal scheduling[J]. IEEE Transactions on Power Systems, 1998, 13(2): 501- 518.
[5]王亚娟, 熊信艮. 基于遗传算法的水火电混合电力系统短期发电计划优化[J]. 继电器, 2000, 28(10): 21- 24.
[6]DHILLON J S, PARTI S C, KOTHARI D P. Fuzzy decision-making in stochastic multiobjective short-term hydrothermal scheduling[J]. IEE Proceedings of Generation,Transmission and Distribution, 2002, 149(2): 191- 200.
[7]STORN R, PRICE K. Differential Evolution-a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J]. Journal of Global Optimization, 1997, 11(4): 341- 359.
[8]汪慎文, 丁立新, 张文生, 等. 差分进化算法研究进展[J]. 武汉大学学报: 理学版, 2014, 60(4): 283- 292.
[9]PRICE K. Differential Evolution: A Fast and Simple Numerical Optimizer[A]. 1996. Biennial Conf of the North American Fuzzy Information Processing Society[C]. New York, 1996: 524- 527.
[10]王小平, 曹立明. 遗传算法-理论、 应用与软件实现[M]. 西安: 西安交通大学出版社, 2002.
[11]李凯斌, 卢建刚, 吴燕玲, 等. 改进的差分进化算法及应用[J]. 组合机床与自动化加工技术, 2008, (10): 16- 18.
[12]王文川, 徐冬梅, 邱林, 等. 差分进化算法在水电站优化调度中的应用[J]. 水电能源科学, 2009, 27(3): 162- 164.
[13]卢有麟, 周建中, 覃晖, 等. 差分进化算法在电力系统环境经济调度中的应用[J]. 华中科技大学学报: 自然科学版, 2010, 38(8): 121- 124.
[14]BASU M. An interactive fuzzy satisfying method based on evolutionary programming technique for multi-objective short-term hydrothermal scheduling[J]. Electric Power Systems Research, 2004, 69: 277- 285.
[15]MANDAL K K, BASU M, CHAKRABORTY N. Particle swarm optimization technique based short-term hydrothermal scheduling[J]. Applied Soft Computing, 2008, 8(4): 1392- 1399.
[16]胡国强. 梯级水电站群优化调度与运营策略研究[D]. 天津: 天津大学, 2005.
[17]李英海. 梯级水电站群联合优化调度及其决策方法[D]. 武汉: 华中科技大学. 2009.
(责任编辑 陈 萍)
Short-term Dispatch Study of Hydrothermal Power Systems Based on Enhanced Differential Evolution
HUANG Di1, XU Gang2,3, XIANG Hongyan1, LI Yinghai2
In view of the complexity and difficulty to decide the mutation rate in high-dimensional problems such as short-term dispatch of hydrothermal power systems and premature convergence problem in Differential Evolution (DE), an Enhanced Differential Evolution (EDE) algorithm is proposed. In EDE, a self-adaption mutation operator is adopted. Thereafter, the distance variance is used to check the premature convergence, and new population is generated by normal distribution. A deputy fitness function is constructed in order to make the feasible solution be within the constraints of convergence. From the analysis of simulated system consisting of four hydropower stations and three thermal power stations, it can be seen that the EDE gives a minimum cost of system and provides an effective method for the optimization of hydrothermal power systems.
enhanced differential evolution algorithm; cascade hydropower station; joint optimal dispatch; hydrothermal power system

2015-12-18
国家自然科学基金资助项目(51409152)
黄迪(1989—),男,湖北洪湖人,硕士,从事水电站运行工作;徐刚(通讯作者).
(1. Hubei Qingjiang Hydroelectric Development Co., Ltd., Yichang 443000, Hubei, China;2. College of Hydraulic & Environmental Engineering, China Three Gorges University, Yichang 443002, Hubei, China;3. Hubei Provincial Collaborative Innovation Center for Water Resources Security, Wuhan 430072, Hubei, China)
TV697.1
A
0559- 9342(2017)05- 0076- 05

