基于小波消噪技术的投影寻踪自回归预报模型
魏 鹏
(雅砻江流域水电开发有限公司,四川成都610051)
基于小波消噪技术的投影寻踪自回归预报模型
魏 鹏
(雅砻江流域水电开发有限公司,四川成都610051)
针对径流序列呈现出的随机性和非线性等,基于耦合小波分析理论的降噪功能以及投影寻踪自回归模型的非线性逼近功能,建立一种组合预报模型,即PPAR-WDT。模型运用Mallat算法将径流序列进行分解;然后利用阈值消噪技术对含有噪声的高频信号序列进行降噪处理,最后重构新序列;运用投影寻踪自回归模型进行预报。将新组合模型应用于某水文站中长期径流预报的结果表明,相比于单一投影寻踪自回归等3种模型,PPAR-WDT模型具有更高的预报精度和更好的稳定性。
径流预报;小波消噪技术;Mallat算法;投影寻踪自回归;组合模型
0 引 言
径流预报对防洪减灾以及水能资源的高效利用有着重要作用。受气候环境和人类活动等多种因素影响,径流序列表现出强烈的模糊性、随机性、非线性等特点[1];因此,径流预报模型一直是水文水资源领域中的热点及难点问题之一。目前,较常用的预报模型有多元回归模型[2]、神经网络模型[3]、支持向量机[4]等;但在实际运用中仍受到不同程度的限制。如:多元回归模型的求解函数比较复杂,在预报非线性序列时精度难以得到保证;BP模型存在收敛速度较慢、训练时间较长等不足;支持向量机中参数优化比较复杂;等等。因此,研究新模型以提高径流预报精度仍然具有极为重要的现实意义[5- 6]。
小波分析理论(Wavelet Analysis Theory)作为一门数学分支学科,近些年在各领域已有较为出色的表现[7-10]。其框架下的小波消噪技术(Wavelet De-noising Technology,WDT)能对含噪声的信号序列进行降噪处理。利用这一技术对径流序列进行消噪处理,可在一定程度上减少水文序列中的干扰成分,进一步把握其内在变化规律。基于投影寻踪自回归技术(Projection Pursuit Auto Regression,PPAR)具有较强的处理高维数据的能力,可解决非正态、非线性的问题的优点[11]。鉴于目前尚无文献涉及二者的结合,本文将WDT和PPAR进行耦合,建立基于小波消噪技术的投影寻踪自回归模型(Projection Pursuit Auto Regression Model based on Wavelet De-noising Technology, PPAR-WDT),探求进一步提高径流预报精度的改进方法。
1 小波消噪技术
1.1 小波变换
小波消噪技术源自小波分析理论,其重要基础是小波变换。设时间序列为s(t),则其变换形式为
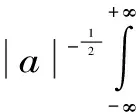
(1)
式中,Ws(a,b)为变换系数;a为频域因子;b为时域因子;Ψ(t)为母小波函数;*表示复共轭;t为时间。
然而在实际运用中,s(t)常是离散状态。因此,对式(1)作离散形式的转变。即
(2)
式中,N为离散总数;Δt为时间间隔。
从式(1)、式(2)可看出,Ws(a,b)耦合了时间序列s(t)和母小波函数Ψ(t)的信息,可反映序列频域和时域的性质。亦即,如果频域因子a较小,则频域的分辨率较低,对时域的分辨率较高;反之,如果频域因子a较大,则对频域的分辨率较高,对时域的分辨率较低。因此,可利用小波变换对时间序列进行多尺度分频分析。
1.2 Mallat算法
Mallat算法是实现小波变换的一种经典算法,也称为快速小波算法(Fast Wavelet Algorithm,FWA)。其包括分解和重构两部分,以此对s(t)进行分解与重构,实现上述小波变换功能。
分解
(3)
重构
(4)

可以看出,滤波器是Mallat算法的核心技术,不同的母小波函数Ψ(t)拥有不同的低通滤波器和高通滤波器。对于不规则信号而言,Daubechies小波系列(dbN)能较为敏感地反应其特征,而相比于该系列其他小波,db4小波的时窗更短,分辨率更高[12]。鉴于径流预报的非线性等特征,本文的母小波函数Ψ(t)选用db4小波
1.3 小波消噪
在上述算法基础上,对s(t)进行噪声消除的处理。设
s(t)=f(t)+e(t)
(5)
式中,f(t)为有用信号;e(t)为白噪声信号。
利用式(3)对s(t)作小波分解,e(t)主要表现在各分辨尺度对应的高频成分中;此时运用阈值法[13]对高频成分进行处理,方可实现信噪分离。
2 基于小波消噪技术的投影寻踪自回归预报模型
2.1 基本原理
建立多种方法交叉组合的预报模型时,方法间的结合方式成为研究关键,也直接影响着预报结果的精度。本文将WDT融入PPAR模型中,建立PPAR-WDT模型(见图1),基本原理为:利用Mallat算法中的分解公式对原始序列进行分解,得到高频成分和低频成分,对含噪的高频部分进行消噪处理,再加以重构,使消噪后的数据更能反映径流序列的本质及变化规律。在此基础上,利用PPAR模型进行预报。
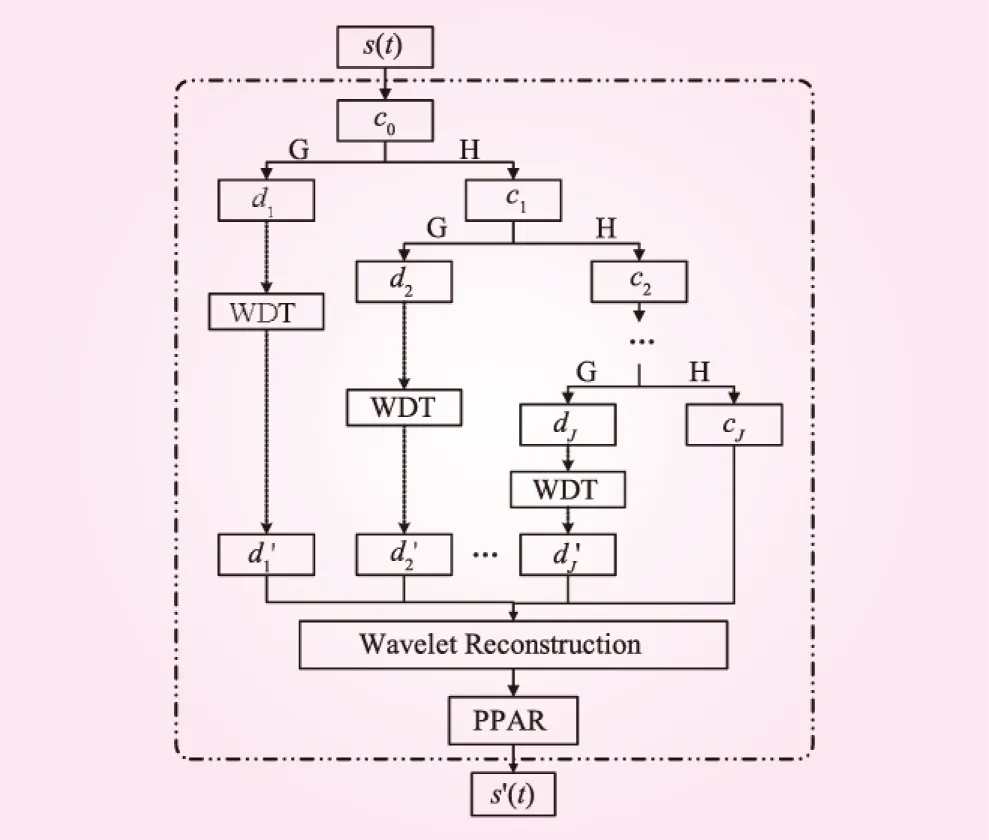
图1 PPAR-WDT模型结构示意
2.2 模型构建
在上述基本原理框架下,构建PPAR-WDT模型,具体步骤如下:
Step1。选择db4小波为母小波函数,采用Mallat分解算法对时间序列s(t)进行J层分解,得到分解序列{cJ(t),dJ(t),dJ-1(t),…,d1(t)}。
Step2。对1~J层的每一层高频序列dj,选择一个阈值Fσ进行阈值量化处理,得到消噪后的高频成分dj′。本文利用Stein无偏风险法[14]进行阈值估算,并采用软阈值方式进行阈值量化处理
(6)
Step3。由第J层的低频序列cj和消噪后的1~J层的高频序列dj′,利用Mallat重构算法进行重构,得到消噪序列s′(t)。
Step4。运用自相关技术,选取各分解序列的预报因子。为简洁阐述过程,令序列统一为xi(i=1,2,…,n),并设Rk(k=1,2,…,m)为xi延迟k步的自相关系数,则
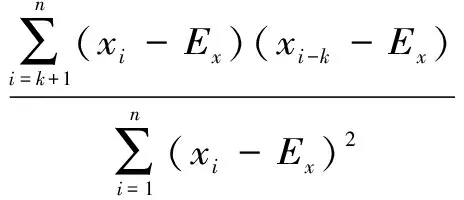
(7)
式中,n为序列容量,m (8) 那么,xi-k的自相关性显著,此时可其选为预报因子。 Step5。确定投影值 (9) 式中,uk为投影方向;p为预报因子数目。 Step6。建立预报模型 (10) 式中,x′为预报值;h为Hermite多项式;v为h的系数;M为岭函数的个数;r为h的阶数。 Step7。建立投影指标函数,并采用基于实数编码的加速遗传算法进行优化,确定参数u、v: (11) Step8。令拟合残差r=xi-xi′,若满足精度要求,则可确定模型参数,输出预报结果;否则,用r替换x,返回Step4进行循环计算,直到满足条件为止。 基于MATLAB编程语言,利用某水文站1956年~2005年(共计50 a)实测年径流数据资料进行实例计算,以验证新模型的合理性。令径流序列为{Q(t)|t=1,2,…,50},模型参数设置如下:分解尺度J=3,置信水平取70%,延迟步数m=11,岭函数个数M=1,多项式的阶数r=8。首先,运用db4正交小波,采用式(3)对Q(t)进行分解,得到对应的小波分解序列{c3(t),d3(t),d2(t),d1(t)}(见图2)。 图2 宜昌站年径流序列(1956年~2005年)小波分解 由图2可以看出,低频序列c3(t)包含了原始序列的趋势成分;高频序列dj(t)(j=1,2,3)为包含了其随机成分,且扰动程度随分解尺度的增加而降低。 在此基础上,依据式(6)对包含噪声的d1(t)、d2(t)、d3(t)序列进行消噪处理,得到d1′(t)、d2′(t)、d3′(t),并利用式(4)对消噪后的新序列{c3(t),d3′(t),d2′(t),d1′(t)}进行重构,得到Q*,结果如图3所示。 图3 径流序列消噪前后对比 从图3可以看出,消噪序列Q*保持了原始序列Q的主要趋势信息;同时,在一定程度上受到随机成分(噪声)扰动的影响较小。 进一步将Q*作为输入项,依据式(7)进行计算,选取预报因子。计算结果如表1所示。 表1 Q*自相关系数及其上、下限值 图4 不同模型预报结果 由表1可以看出,当k取4和5时,满足式(8)所给条件;则Q*的预报因子为x(Q*)i-4、x(Q*)i-5。 依次遵循Step5~Step6进行计算,确定模型关键参数u、v,并输出预报结果(表2、表3、图4)。同时,选取PPAR模型、BP模型以及自回归滑动模型(ARMA)对同一径流序列进行预报。此处采用拟合样本标准均方误差(IP1)、检验样本相对误差平均值(IP2)以及波动性(IP3)三项指标,分别从模型预报精度和预报结果稳定性两方面对各模型性能进行评价。即 (12) (13) (14) 式中,X为拟合样本的总数;Y为检验样本的总数;s2为检验样本方差;xsi、xyi分别为拟合样本中第i个序号的实测值和预报值;xsj、xyj分别为检验样本中第j个序号的实测值和预报值;σt、σp分别为第t、p个序号的相对误差。各模型的性能评价指标和预报结果如表3、图4所示。 表2 参数u、v 表3 不同模型性能评价指标 % 由表3可以看出,在预报精度方面,对于拟合样本,除ARMA模型的IP1值较大外,其他3种模型的拟合效果均较好;对于检验样本,PPAR-WDT模型预报效果最佳,IP2值为4.23%,小于其他3种模型。在预报结果稳定性方面,PPAR-WDT模型的IP3值最小,其稳定性最好。综上所述,由于PPAR-WDT模型利用小波消噪技术进行了数据预处理,较大程度地降低了随机成分的干扰,较好地提取了序列中有用信息,同时结合了PPAR模型很好的非线性逼近功能。因此,与其他3种模型相比,本模型PPAR-WDT预报效果最佳,可服务于水库调度等作业。 本文有机地将小波消噪技术与投影寻踪自回归模型相结合,构建了一种新的组合预报模型。相比于其他单一或者组合模型,其显著优势在于对序列进行了降噪处理,宏观上净化了序列,极大程度地排除了噪声信号对客观趋势判断的干扰,更能揭示序列变化水平。在某水文站实测年径流预报应用中验证了新模型可较充分地挖掘径流序列的有效信息,在预报精度和稳定性方面都有明显提高,可作为径流预报的一种有效途径。 [1]刘蕊鑫, 纪昌明, 马源. 基于互信息的改进RBF神经网络预测模型及其应用[J]. 中国农村水利水电, 2016(10): 100- 103, 115. [2]王秀杰, 练继建, 费守明, 等. 基于小波消噪的混沌多元回归日径流预测模型[J]. 系统仿真学报, 2007, 19(15): 3605- 3608. [3]莫崇勋, 王大洋, 钟欢欢, 等. 人工神经网络在澄碧河年径流预测中的应用研究[J]. 水力发电, 2016, 42(9): 25- 28. [4]朱双, 周建中, 丁小玲, 等. 基于GM-SVR耦合的月径流预测模型研究与应用[J]. 水力发电, 2015, 41(12): 17- 20. [5]KALTEH A M. Monthly river flow forecasting using artificial neural network and support vector regression models coupled with wavelet transform[J]. Computers & Geosciences, 2013, 54: 1- 8. [6]ADAMOWSKI J, SUN K. Development of a coupled wavelet transform and neural network method for flow forecasting of non-perennial rivers in semi-arid watersheds[J]. Journal of Hydrology, 2010, 390(1- 2): 85- 91. [7]赵鲲鹏, 赵二峰, 王莹, 等. 提升小波多尺度分解法与RBF神经网络在混凝土重力坝应力监测中的应用[J]. 水力发电, 2015, 41(2): 81- 85. [8]童超, 刁鸣, 杨承志. 独立分量分析联合小波变换的多分量信号调制识别研究[J]. 科学技术与工程, 2016(30): 258- 263. [9]郑健, 谢先武, 刘胜. 利用小波分析的高铁沉降变形预测[J]. 测绘科学, 2016(4): 1- 6. [10]孙永辉, 范磊, 卫志农, 等. 基于小波分析和集成学习的光伏输出功率短期预测[J]. 电力系统及其自动化学报, 2016(4): 6- 11, 30. [11]纪昌明, 李荣波, 张验科, 等. 基于小波分解的投影寻踪自回归组合模型及其在年径流预测中的应用[J]. 水力发电学报, 2015, 34(7): 27- 35. [12]刘力, 周建中, 李英海, 等. 基于小波消噪的混沌径流预测模型[J]. 华中科技大学学报: 自然科学版, 2009(7): 86- 89. [13]刘国华, 钱镜林, 王建江. 小波软阈值技术和人工神经网络在洪水预报中的研究[J]. 水力发电学报, 2004(4): 5- 10. [14]郭金吉. Fuzzy度量空间映射对的几个不动点定理[J]. 南京工业大学学报: 自然科学版, 1993(1): 69- 73. (责任编辑 陈 萍) Projection Pursuit Auto Regression Forecasting Model Based on Wavelet De-noising Technology WEI Peng Considering the randomness and nonlinearity of runoff series, the Projection Pursuit Auto Regression model based on Wavelet De-noising Technology (PPAR-WDT) is proposed which combines the de-noising function of wavelet analysis theory with the nonlinear approximation function of the Projection Pursuit Auto Regression (PPAR). In this model, the runoff is firstly decomposed into several high-frequency signals and a low-frequency signal by Mallat algorithm, and then, each high-frequency signal is processed and reordered by wavelet de-noising technology to eliminate noise effects, which enables the processed signals to be reconstructed in a new runoff series. The application of this new combined model in the runoff forecast of a hydrologic station shows that PPAR-WDT model has higher forecasting accuracy and better stability comparing with other three different kinds of forecasting models. runoff forecast; wavelet de-noising technology; Mallat algorithm; projection pursuit auto regression; combined model 2016- 12- 23 魏鹏(1981—),男,四川简阳人,高级工程师,博士,研究方向为系统工程、水能资源开发与利用. P338.2 A 0559- 9342(2017)08- 0034- 05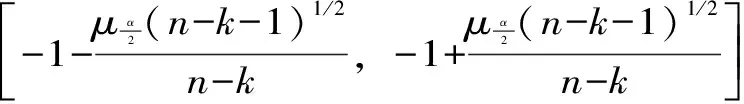
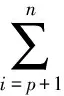

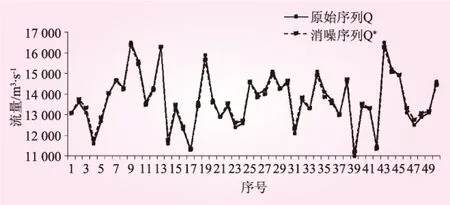
3 实例应用

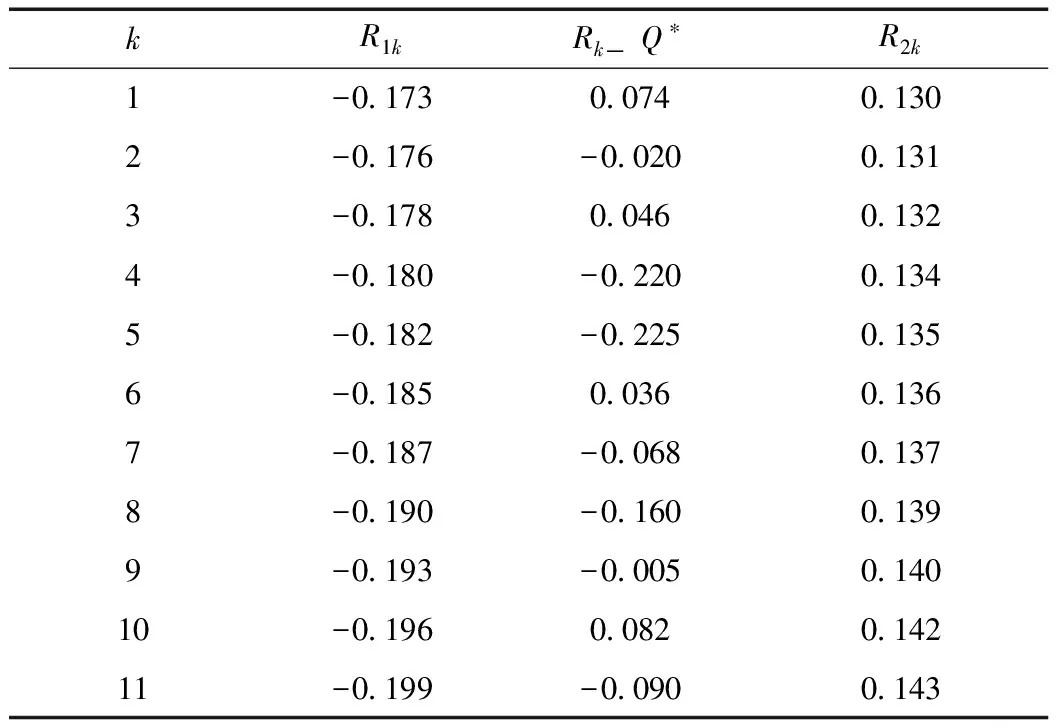



4 结 论
(Yalong River Hydropower Development Company Ltd., Chengdu 610051, Sichuan, China)

