高压天然气长输管网内天然气的相平衡计算
鲍玲玲,刘 杰
1.中国建筑科学研究院建研科技股份有限公司,北京 100013
2.中国石油天然气勘探开发公司,北京 100034
高压天然气长输管网内天然气的相平衡计算
鲍玲玲1,刘 杰2
1.中国建筑科学研究院建研科技股份有限公司,北京 100013
2.中国石油天然气勘探开发公司,北京 100034
天然气各组分含量是评价天然气品质和污染程度的重要参数。目前,天然气各组分含量一般通过气相色谱仪来测定,在没有条件进行色谱测量的情况下,可以采用天然气相平衡计算方法来预测长输管网天然气各组分变化情况。建立了长距离、高压天然气输送管网内气体相平衡数学模型,并给出了相应计算方法。用该模型和求解方法对西气东输管网内进行了相平衡模拟计算,并与实测结果进行了比较。结果表明:预测结果与实测结果基本吻合,所建立的数学模型和计算方法可靠,能够较精确地预测长输管网内天然气的各组分含量、水力参数、物性参数、相平衡参数等。
相平衡;物性参数;天然气长输管网;组分含量;发热量;环保品质
天然气组分中甲烷(CH4)含量占90%以上,烯烃类物质(碳2以上碳氢化合物)含量约9%,还有微量的气态水(H2O)和硫化氢(H2S)。天然气燃烧后产生有害气体,如一氧化碳、二氧化碳、硫化氢、氧化硫等。长期以来天然气采用体积计量,即不管天然气组分如何、发热量和品质是高或低,均是相等价格,这是不合理的。天然气进行能量计量是科学可取的,应通过天然气各组分含量来评价天然气品质的好坏、发热量的高低和燃烧后的污染程度,即甲烷含量越高、重烃含量越低、硫化氢和二氧化碳含量越低,则天然气品质越好,发热量越高,污染越小。因此采用天然气各组分含量来评价天然气品质好坏、发热量高低和污染程轻重则更为科学合理。
天然气各组分含量一般通过专用气相色谱仪进行测定,气相色谱仪利用色谱柱先将混合物分离,然后利用测量仪依次测量已分离出来的组分。但是,许多输气管网没有条件进行色谱测量,因此研究天然气管道各组分含量和物性参数随管道长度、流速、时间等因素变化规律则十分必要[1]。
通过分析影响天然气管道内流动的各种因素,本文建立了长距离高压天然气输送管网内天然气的相平衡数学模型,并给出了相应的计算方法。只要已知天然气管网首站气源处天然气的各组分含量及压力、温度等参数,便可以计算出管网不同位置和环境下天然气各组分含量,相平衡参数以及流量、密度等物性参数。为了提高天然气在高压、低温下的计算精度,需要采用多参数状态方程,因而选用了文献中公认的精度较高的实际气体状态方程——BWRS状态方程[2],即Benedict-Webb-Rubin-Starling方程作为临界参数、物性参数及相平衡参数计算的基本方程。
1 模型建立及计算方法
1.1 气体管流的基本方程
由于气体的运动必然满足质量守恒、动量守恒和能量守恒,故由流体力学可建立气体流动相应的连续性方程、能量方程、运动方程和气体状态方程。这些方程描述了气体的压力、密度、流速和温度、压缩因子等量之间的关系。这些方程分别如下[3-5]:
(1)质量守恒(连续方程):

(2)动量守恒(运动方程):

(3)能量守恒(能量方程):

(4)气体状态方程:

式中:Q为工程标准状况下的输气管道体积流量,m3/s;p为压力,Pa;ρ为气体密度,kg/m3;v为管道内气体流速,m/s;μ为气体动力黏度,Pa·s;h为气体焓,kJ;x为管轴长度,m;s为高程,m;θ为管道与水平线之间的夹角(°);g为重力加速度,m/s2;λ为水力摩阻系数;D为管道内径;m;T为气体温度,K;R为气体常数,kJ/(kmol·K)。式(4)中A0,B0,C0,D0,E0,α,b,c,d,a,γ为状态方程式的11个参数。对于天然气各纯组分i的这11个参数,均可由它的临界参数Tci、pci及偏心因子ωi从经验公式求得[4]。
1.2 有高程的长距离输气管道稳态运行的模型研究
对于任一坡度的直管段,若忽略气体流速增大的影响,则流量计算方程可以写为[5-6]:

式中:ds为dx段上的高程变化。
设l为任一坡度的直管段长度,Δs为坡度终点与起点的高程差,将上述各式带入式(5)得到:
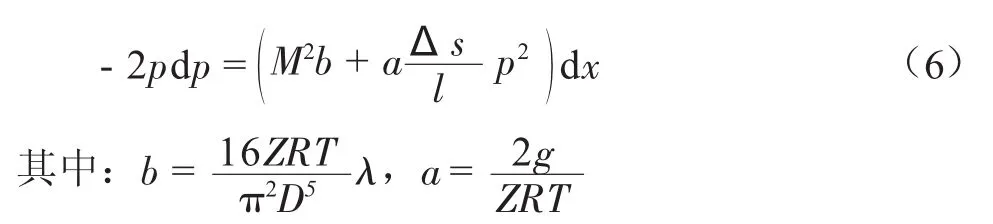
设全程管道中间各计算点压力相应为p1,…,pZ-1,中间各点距离为l1,l2,…,lZ,管段起点至终点的总距离为L(L=l1+l2+…+lZ),各点高程为sQ,s1,s2,…,sZ。
整理为:

式中:pQ为输气管计算段的起点压力,Pa;pZ为输气管计算段的终点压力,Pa;sQ为输气管计算段的起点高程,m;sZ为输气管计算段的终点高程,m;l为输气管计算段的长度,m;M为质量流量,kg/s;Z为天然气的压缩因子;Δ*为天然气的相对密度;C0为工程标准状况下天然气的比热容,J(kg·K)。
在程序计算过程中,根据用户选择的步长Δx将管道分为多个小的管段,在每一个小段的末端应用公式(7),根据起始端压力计算每一个小段末端的压力值,最终计算得出整根管道的压力分布。
1.3 天然气管网相平衡模型[7-8]
通过上述模型可以计算出长输管道各节点的流量F(kmol/h)和压力p(MPa)。已知温度T(K)和天然气各组成含量zi(摩尔分数%),将上述计算值和已知值代入相平衡模型中,可以判断多组分气体是否进行气、液两相分离,并预测出分离气相流量V(kmol/h),气相各组分含量yi(摩尔分数%);同时计算出液相流量L(kmol/h),液相各组分含量xi(摩尔分数%),各组分平衡常数Ki[9]。
相平衡方程为:

按组分物料平衡方程:

摩尔气化分率e定义为:

将方程(10)代入方程(11)消去yi可得,


式中:c为组成总数(组分总数)。
选用Newton-Raphson[10]法求解e的非线性方程:

式中:下标k表示迭代次数。
按指定平衡状态下的p、T,由平衡常数的经验方程求得各组分的Ki值,并假设e的初值e1,求出f(e1)和f′(e1),代入式(15)即可求得下次迭代用的e2。依次重复进行,直到︳f(e)︳小于指定的允许偏差为止。
1.4 利用BWRS方程计算气、液相密度
首先需要根据长输管道流动模型计算出各节点平衡p,T,并已知起点天然气各组分含量zi,由公式(16)求解气相或液相的密度ρv或ρL。密度根一般用正割法迭代求取[7-16]:
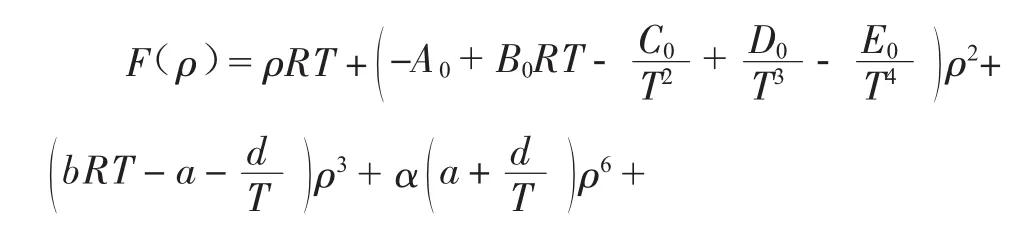
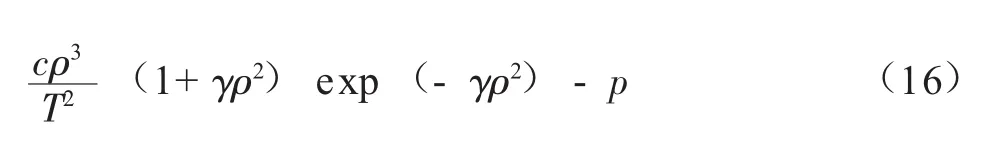
求解在指定p,T和zi下F(ρ)=0时的ρ值。正割法的迭代公式为:
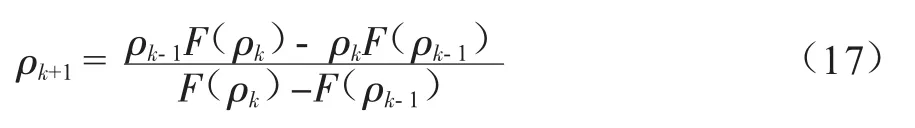
式中下标k为迭代次数。应用正割法时需设两点密度初值。取初值ρ1和ρ2,分别按式(16) 求出F(ρ1)和F(ρ2)后,应用式(17)依次求定下一次迭代用的ρ值,直到得到满足精度要求的解。
1.5 利用BWRS方程计算各组分逸度
由BWRS方程导出的各组分逸度公式如下[7-16]:
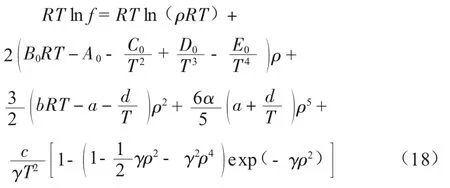
通过公式(18)计算得到天然气各组分逸度,进而准确得出天然气物性参数和相平衡参数。
2 计算结果及其实例验证
西气东输管道西起新疆塔里木的轮南油田,向东最终到达上海,延至杭州。途经11省区,全长4 000km。设计年输气能力120亿m3,最终输气能力200亿m3。
西气东输管道沿途共设置28个站,各站的里程、站间距和高程见表1。
已知西气东输管道轮南首站的压力、流量、温度和气质分析数据(天然气各组分含量),将上述已知数据代入本文建立的计算模型中,计算出沿途博爱站和终点上海站的水力参数、物性参数和相平衡参数,其中天然气各组分摩尔分数的计算值与测量值的对比见表2,各参数值见表3。
从表1~3中可以看出随着西气东输管道输送距离的增加,天然气压力、密度的计算值逐渐降低,同时天然气中甲烷的含量逐渐降低,乙烷等和其他重质烷烃各组分含量均升高,计算结果说明随着输送管道距离的增加,天然气的品质逐渐降低。
需要说明的是,实际测量是利用气相色谱仪在博爱站和上海站进行天然气组分含量检测,相比通过气袋取样检测较为准确。测量结果表明:相比轮南首站天然气各组分含量测量值,博爱站和上海站天然气甲烷的测量值逐渐降低,乙烷和其他重质烷烃各组分含量的测量值均逐渐升高。
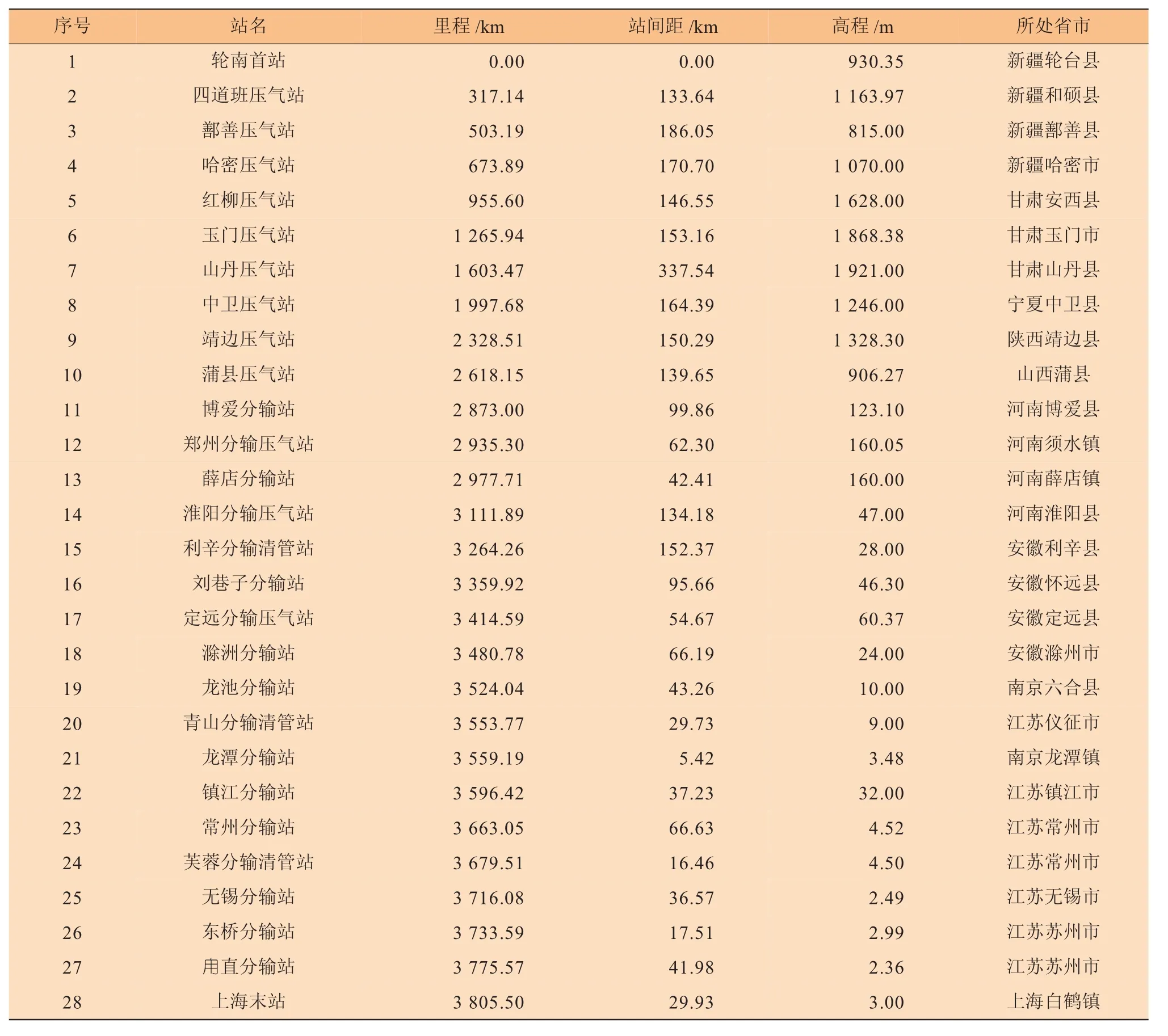
表1 西气东输管道各压气站场设置

表2 西气东输管道沿程天然气各组分含量(摩尔分数)的计算值和测量值比较/%
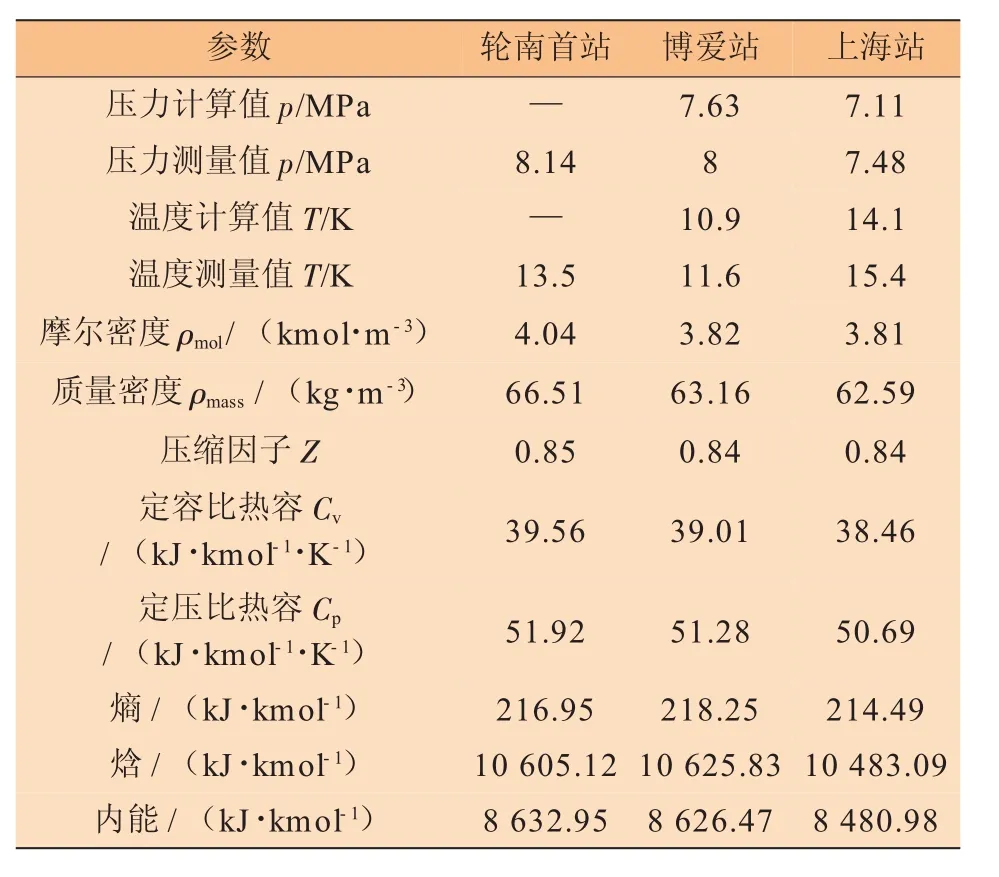
表3 西气东输管道博爱站和上海站天然气物性参数计算值
通过表2可以看出:西气东输管道沿程各站中天然气各组分含量的计算值和测量值均符合长输管道天然气各组分的变化规律。沿程各站中天然气各组分含量的计算值和测量值相差较小,但存在误差,博爱站最小误差0、最大误差33%、平均误差16.92%,误差在允许范围之内;上海站最小误差0、最大误差37.5%、平均误差10.38%,误差也在允许范围之内。通过上述分析得出:博爱站和上海站的计算结果合理、较为精确。
3 结论
本文首次提出了长距离天然气输送管网内天然气相平衡数值计算方法。通过西气东输管道沿程天然气的相平衡计算实例验证,表明所采用的数学模型和数值计算方法是可靠的,可以较精确地预测出长距离天然气输送管网沿程的流动参数、天然气物性参数和各组分含量等参数。从相平衡的角度对长输管道沿程中天然气的品质和各组分含量的变化情况进行分析,得出:随着输送距离的增加,压力变小,天然气中甲烷含量逐渐降低,其他重质烷烃类含量逐渐升高,天然气品质逐渐降低,发热量降低,燃烧后污染较大。因此可以根据预测结果,进一步在各站点采用相应的技术措施降低长距离输送管网内天然气H2S含量、CO2含量和其他重质烷烃类含量,从而提高天然气的品质,减少燃烧后的污染,同时保障输送安全。
[1]LIU Hengwei,LIU Zhongliang,FENG Yongxun,et al.Characteristics of supersonic swirling dehydration system of natural gas[J].Chinese J.Chem.Eng,2005,13(1):9-12.
[2]高光华,童景山.化工热力学[M].北京:清华大学出社,2007:60-61.
[3]冯叔初,郭揆常,王学敏.油气集输[M].东营:石油大学出版社,1988:292-295.
[4]姚光镇.输气管道设计与管理[M].东营:石油大学出版社,1991:56-79.
[5]李长俊.天然气管道输送[M].北京:石油工业出版社,2000:6-48.
[6]苏尔皇.管道动态分析及液流数值计算方法[M].哈尔滨:哈尔滨工业大学出版社,1985:31-49.
[7]BAO Lingling,LIU Zhongliang,LIU Hengwei,et al.Phase equilibrium calculation of multi-component gas separation of supersonic separator[J].Science China Technological Sciences,2010,53(2):435-443.
[8]郭天民.多元气-液平衡和精馏[M].北京:石油工业出版社,2002:173-180.
[9]STARLING KE,HAN M S.Thermo data refined for LPG(Part 14:Mixture)[J].Hydrocarbon Processing,1975,51(5):129.
[10]文世鹏,张明.应用数值分析[M].北京:石油工业出版社,2001:177-180.
[11]苏长荪.高等工程热力学 [M].北京:高等教育出版社,1987:48-67.
[12]吴玉国,陈保东.BWRS方程在天然气物性计算中的应用[J].油气储运,2003,22(10):16-21.
[13]童景山.流体的热物理性质[M].北京:中国石化出版社,1996:17-54.
[14]童景山,李敬.流体热物理性质的计算[M].北京:清华大出版社,1982:56.
[15]郑德馨,刘芙蓉.多组分气体分离[M].西安:西安交通大学出版社,1988:102.
[16]STANLEYM,WALAS.Phase equilibria in chemicalengineering [M].Boston:Cambridge University Press,1985.
Phase equilibrium calculation of long-distance natural gas transportation pipeline network
BAO Lingling1,LIU Jie2
1.CABR Technology Co.,Ltd.,China Academy of Building Research,Beijing 100013,China
2.China NationalOiland Gas Exploration and Development Corporation,Beijing 100034,China
The component contents of natural gas are the important parameters for evaluating natural quality and pollution level.At present,the component contents of natural gas are usually determined by the gas chromatography,but there aren't enough conditions to take chromatographic measurement for many gas pipelines.In such case,the calculation method for natural gas phase equilibrium can be used to predict the change of natural gas component contents of long-distance pipeline network.A mathematical model for phase equilibrium prediction of multi-component gas inside the long-distance high-pressure natural gas pipeline network is established and an efficient numerical solution method is designed.The model and the numerical method are used to predict the phase equilibrium characteristics of West to East Gas Pipeline.The predicted results are generally in good agreement with the tested results,which proves that the phase equilibrium model and the solution method are both reliable and accurate,and can be used for the prediction of hydraulic parameters,phase equilibrium parameters and physicalparameters.
phase equilibrium;physical parameters;long-distance natural gas pipeline network;component contents; heating value;environmentalquality
鲍玲玲(1979-),女,天津人,副研究员,2011年毕业于北京工业大学热能工程,博士,主要从事超音速分离管研发、天然气脱水、多相流相平衡、暖通计算、建筑BIM等研究工作。
2017-02-13
10.3969/j.issn.1001-2206.2017.04.004
Email:baolingling@cabrtech.com。

