GPS载波相位测量与伪距测量的组合解算── GNSS卫星导航定位方法之九

刘基余

（武汉大学测绘学院，武汉 430079）

GPS载波相位测量与伪距测量的组合解算── GNSS卫星导航定位方法之九

刘基余

（武汉大学测绘学院，武汉 430079）

采用GPS载波相位/伪距测量值进行组合解算，能够消除电离层效应的影响，提高GPS导航定位的测量精度，本文论证了它们的数学模型。

GPS载波相位测量；GPS伪距测量；电离层效应

1999年1月25日，美国副总统戈尔宣告：21世纪的GPS新型工作卫星（Block IIF）将增设第三个民用信号，其载波频率为1176.45MHz。按计划，而于2010年5月开始向民间用户提供三个导航定位信号：第一民用导航定位信号的载频为1575.42MHz；第二民用导航定位信号的载频为1227.60MHz；第三民用导航定位信号的载频为1176.45MHz。

三个GPS民用导航定位信号实施后，不仅GPS新型工作卫星具有不同于工作卫星Block II/IIA卫星的鲜明特色，而且能将民用实时定位精度提高到空前的新水平。现在讨论用多个GPS载波相位测量值与伪距测量值的组合解算。

1 GPS载波相位测量的简易方程

若暂且忽略一些附加时延，仅考虑电离层效应对站星距离的测量影响，以及载波的相速传播特性，则知第j颗GPS卫星载波相位测量的距离方程为

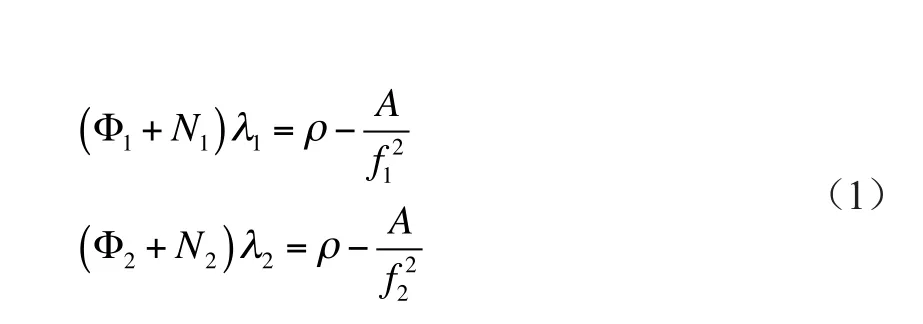
式中，φi为以周为单位的第i个载波的滞后相位观测值（此处，i=1,2，下同）；Ni为第i个载波的整周模糊度（波数）；λi为第i个载波的波长，且知λ1=19cm，λ2=24cm；ρ为以米为单位的站星真实距离；；A为电离层效应引起的距离偏差系数；；ƒi为第i个载波的频率。

若顾及λi=C/fi，则式（1）为

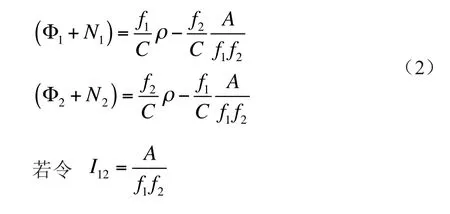
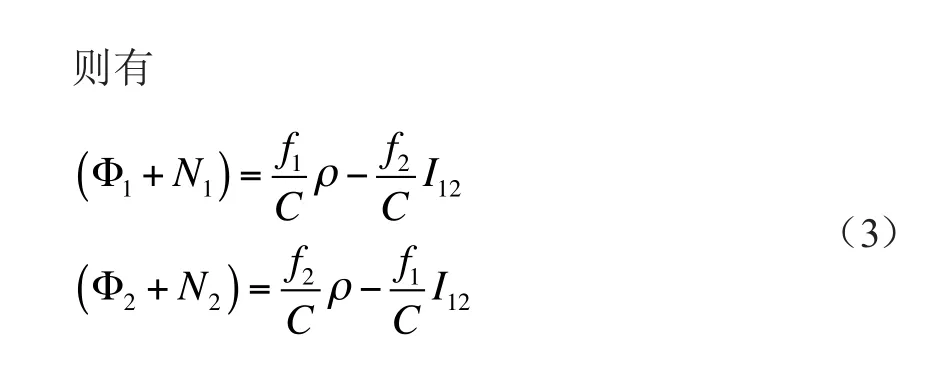
2 宽巷载波相位测量方程式

现将式（3）的两式相减，则得

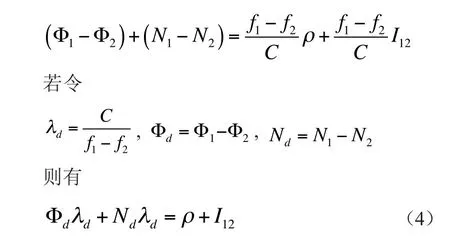
式（4）叫做宽巷（wide-lane）载波相位测量方程式，d称为宽巷载波相位测量波长。且知

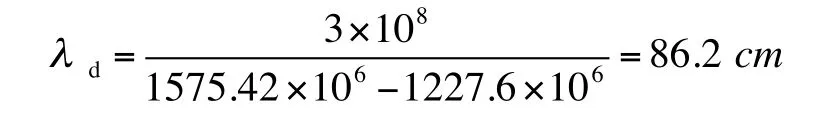
从上可见，采用两个载波（L1,L2）相位测量值进行组合解算，则原拟解算19cm载波波数N1的问题，转化为解算86cm组合载波的宽巷波数Nd。依据L1-P/L2-P互相关测量法，可以用硬件测得宽巷载波相位测量波长λd，以此测得站星距离，解算用户位置。

3 窄巷载波相位测量方程式

如果将式（3）的两式相加，则有

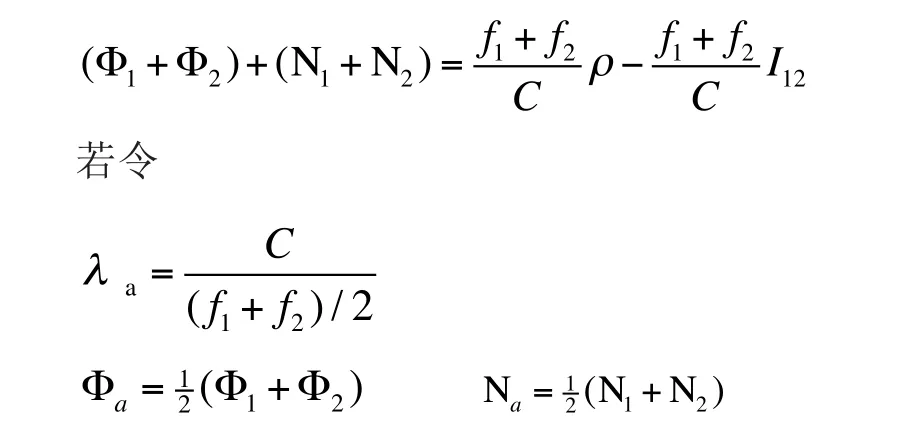
则有

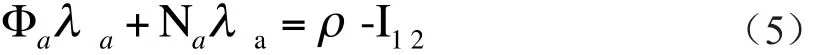
式（5）叫做窄巷（narrow-lane）载波相位测量方程式，λa称为窄巷载波相位测量波长，且知

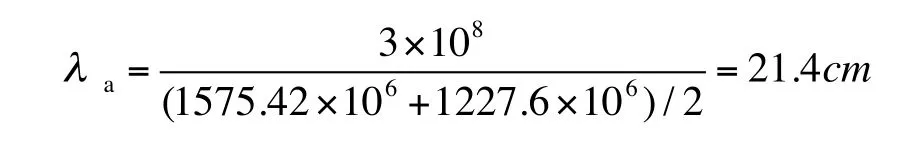
式（5）中的Na为窄巷载波相位测量波数，它是波数N1N2的平均值。

4 L1-P/L2-P码伪距测量的简易方程

以群速传播的L1-P码和L2-P码伪距测量方程分别为

式中，Pi为Li-P码的伪距观测值（i=1,2）；而ρ,fi, A的意义与式（1）相同。

若对式（6）作下列变换

现将式（9）代入式（8），可得

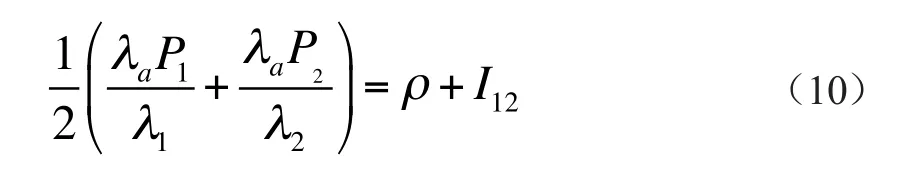
若将式（7）两式相减，则可得

5 宽窄巷载波相位与伪距测量的组合解算

由式（4）和（10）解得

从式（15）可见：用按上述公式算得的宽窄巷载波相位测量值（φdφa），以及它们的波长（λdλa）和波数（NdNa），可以精确地求得站星距离（ρ）；由于采用GPS载波相位/伪距测量值进行组合解算，而消除了电离层效应（I12）的影响；用无电离层效应影响的站星距离（ρ）解算的用户位置，不仅精度较高，而且能够确保用户位置的置信度。

6 三个民用信号的作用非凡

正如前述，GPS新型卫星——Block IIF，增设了第三个民用信号，其载频为f5=1176.45MHz，依前述方法，第二、三载波（L2L5）的相位观测值，也能获得宽巷和窄巷观测方程

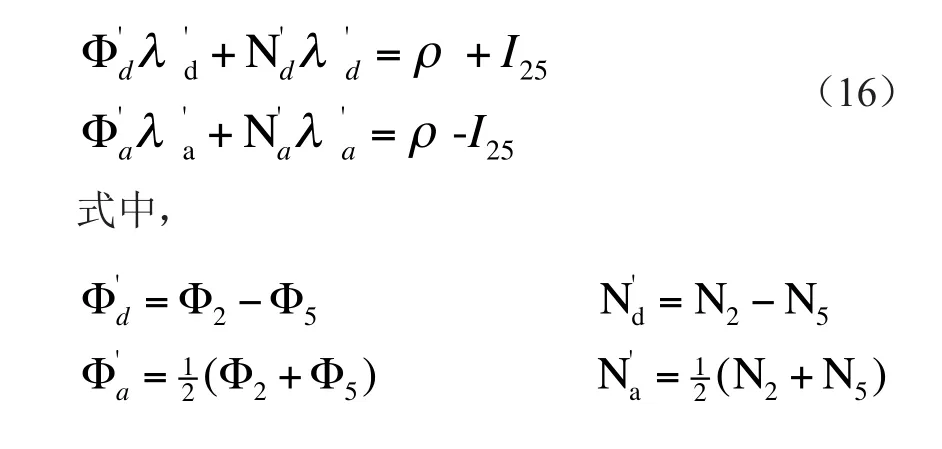
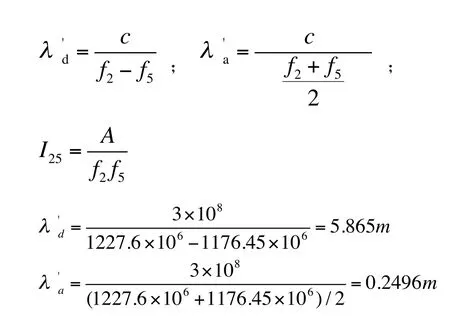
式中，φ5为以周为单位的第三载波（L5）的相位观测值；N5为第三载波的整周模糊度。

仿效式（13）和式（14）的推导方法，则有

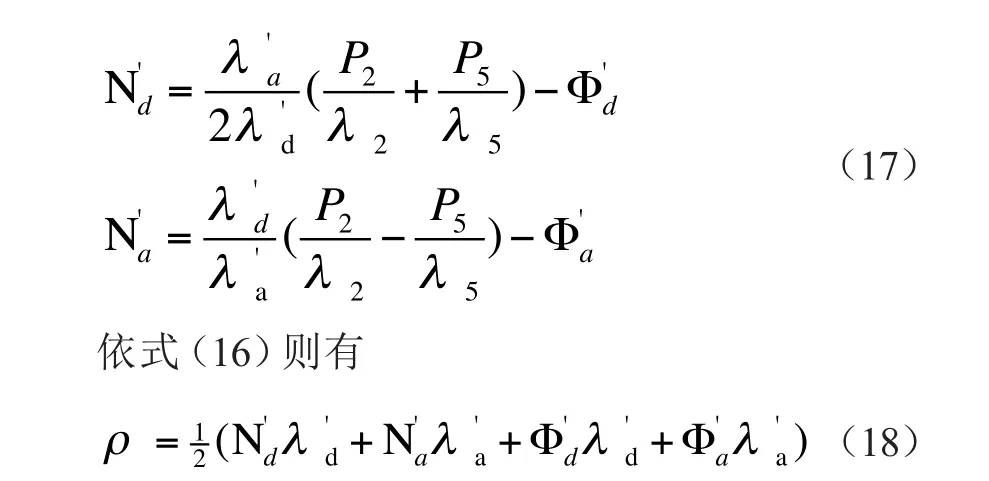
式（18）和式（15）具有相同的作用；即能消除电离层效应的影响，而取得较高而稳定的定位精度。

此外，因λ'd=5.865m，而能更准确地求得波数N'd，有益于用OTF解算实时在航点位。OTF算法的首要问题是，求定载波相位测量整周模糊度的初始值。当用调制在上列三个载波上的一个伪噪声码测得三个伪距（PL1、PL2和PL5）时，则可按下列算式求得载波相位测量整周模糊度的初始值(N0i)：

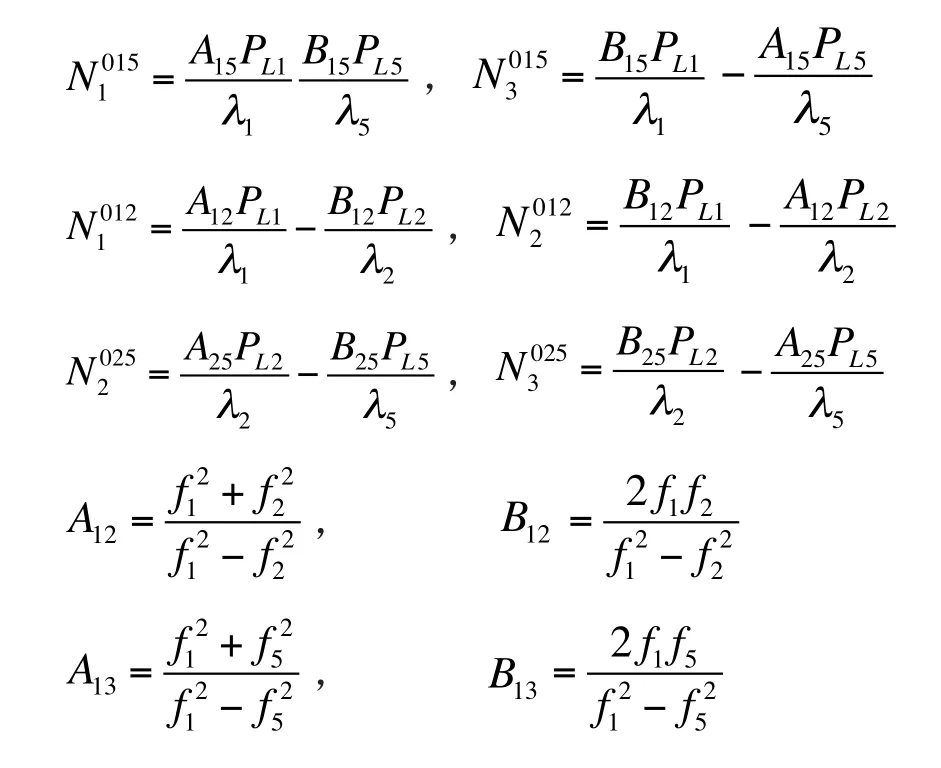
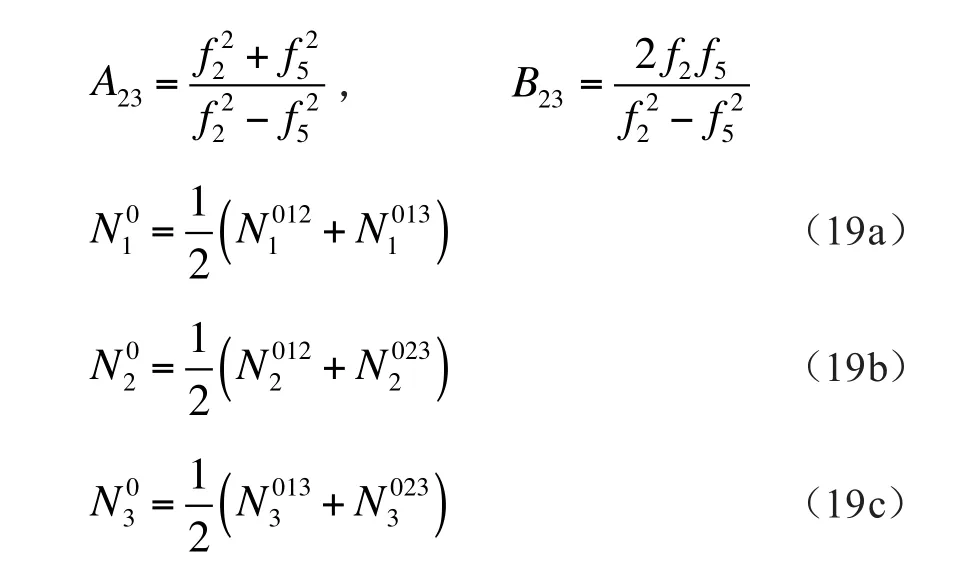
式（19）中的N01、N02和N0

3分别表示第一、二、三载波（L1，L2，L5）的整周模糊度的初始值。当考虑到f1=1575.42HMz，f2=1227.60HMz和f5=1176.45HMz时，算得

A12= 4.09145556, A13= 3.52120865,

A23= 23.51063819；B12= 3.96736797,

B13= 3.37622724, B23= 23.48936160。

故可按所测得的伪距PL1、PL2、PL5和上列AB系数算得整周模糊度的初始值。由此种方法求得的整周模糊度的初始值，比按现行双频观测值求得的整周模糊度的初始值要更接近整周模糊度的正确值，而可缩小整周模糊度的搜索区间；大大加速解算整周模糊度正确值的速度；这可为高动态环境下应用GPS载波相位测量创造了很好的工作基础。

综上可知，随着第三个导航定位信号的增设，以及GPS广播星历的在轨自主更新，对于测地用户而言，能够实现伪距和载波相位测量的无电离层效应影响的组合解算，求解出稳定可靠的5.865m宽巷波数，将超长基线向量的解算精度提高到一个新水平；对于动态用户而言，不仅能够稳获厘米级的实时点位精度，而且能将GPS卫星导航取代现行的所有无线电导航，开创卫星导航的新时代；对于GPS增强系统而言，它的作用将随之而淡化，主要服务于GPS卫星导航定位信号的完好性监测，而不是提高实时点位精度。

[1] 刘基余．GPS卫星导航定位原理与方法（第二版）．北京：北京科学出版社，2008.6

[2] Lachapelle,G., GPS Theory and Applications, University of Calgary, Fall 2000, PP.310

Combinatory Solution with GPS Carrier Phase Measurements and Pseudorange Observations--Method of GNSS Navigation/Positioning (9)

Liu Jiyu
(School of Geodesy and Geomatics, Wuhan University, Wuhan, 430079)

The combinatory solution with GPS carrier phase measurements and pseudorange observations can eliminate the in fl uence of the Ionospheric effect and improve the surveying accuracy of navigation/positioning. In this paper their mathematical models are demonstrated.

GPS carrier phase measurements; GPS pseudorange observations; Ionospheric effect

10.3969/J.ISSN.1672-7274.2017.08.001

TN96

A

1672-7274（2017）08-0001-04