基于分形理论的非饱和土结构吸力定量计算

邓钟尉

(广州市城市规划勘测设计研究院，广东 广州 510060)

基于分形理论的非饱和土结构吸力定量计算

邓钟尉*

(广州市城市规划勘测设计研究院，广东 广州 510060)

已有的研究成果表明，非饱和土强度和变形特性在很大程度上是由结构吸力决定的。本文在可变结构吸力初步表达式的基础上，借鉴分形理论中的有关概念和方法，推导出不等粒径颗粒间可变结构吸力与土体含水量、干密度、孔隙比等的定量计算公式，并从理论上分析了可变结构吸力与含水量、干密度、孔隙比的关系。研究结果表明，可变结构吸力随着含水量的增大单调递减，随着干密度的增大单调递增，随着孔隙比的增大单调递减，与前人理论研究和试验研究结果一致。

非饱和土；分形理论；结构吸力；不等粒径；含水量

1 引 言

吸力[1]是非饱和土力学研究的基础性课题，非饱和土土力学的各种理论(如强度、渗流、变形等)基本上都是围绕吸力这一概念展开的，而对各种吸力的概念和本质认识的正确与否，直接影响到非饱和土有效应力原理及抗剪强度理论的建立。非饱和土的抗剪强度理论，学术界尚无法达成共识，汤连生团队[2～5]的研究结果表明：基于湿吸力及结构吸力的非饱和土有效应力原理概念清晰，物理意义明确，初步阐明了A.W.Bishop单应力状态变量[6，7]中参数χ和D.G.Fredlund双应力状态变量[8，9]中tanФb的物理意义，基于粒间吸力(包括湿吸力和结构吸力)的非饱和土抗剪强度理论，一方面统一了前人的研究成果，另一方面避免了在研究非饱和土强度理论中存在的误区，逐渐为国内外的众多学者所接受。

在很大程度上，土体的强度和变形特性是由结构吸力决定的，文献[3]的理论研究及文献[12]的试验研究均表明：土体结构吸力与含水量、孔隙比和干密度等物理性质密切相关。目前，非饱和土吸力的研究大多是建立在等粒径球形颗粒接触模型基础上的，为研究非饱和土结构吸力与非饱和土土体含水量、孔隙比和干密度等之间的关系，本文假定不等粒径的土颗粒是以Horsfield六方最紧密模型堆积的[21]，基于文献[3]提出的可变结构吸力初步表达式，借鉴分形理论中的有关概念和方法，推导出可变结构吸力的定量计算表达式，并从理论上分析可变结构吸力与含水量、干密度、孔隙比的关系。

2 结构吸力性状初步分析

结构吸力是由水-土化学作用产生的，其来源比较复杂，结构吸力直接作用在土颗粒之间，相当于在土颗粒间产生内拉应力，是有效应力的重要组成部分。结构吸力的影响因素较多，主要受含水量、水溶液的化学性质以及土颗粒的组成及排列的影响，本文着重研究由胶结作用产生的结构吸力。结构吸力按是否受含水量的影响可分为本征结构吸力和可变结构吸力[2～5]。

2.1 本征结构吸力

土体完全饱和后，土颗粒间仍能保持的那部分结构吸力定义为本征结构吸力，与土的某一结构状态相对应。本征结构吸力取决于土体的结构特征，如果土的结构特征发生变化，本征结构吸力也会随之变化甚至丧失，而且是不可恢复的。因此，它只有受到外应力作用而导致土体的结构状态发生改变时，其大小才会发生改变，不随含水量等物理性质的改变而变化[11]。

2.2 可变结构吸力

受土体的含水量、孔隙水压力及与之相关的水化学作用的变化影响的那部分结构吸力定义为可变结构吸力。可变结构吸力随上述各因素的变化而变化的过程是可逆的，这是可变结构吸力与本征结构吸力的根本区别，同时，可变结构吸力还跟土体的含水量、干密度、孔隙比等土体物理状态量密切相关，作为非饱和土有效应力的重要组成部分之一，可变结构吸力对非饱和土的强度有重要的贡献。本文主要研究可变结构吸力。

2.3 初始可变结构吸力

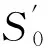
3 可变结构吸力公式推导

从结构吸力的概念可知，其大小和变化规律受到两个因数的影响：一是胶结物和孔隙水溶液的化学成分与含量，该因素决定了土颗粒间单个接触点的结构吸力与其随饱和度的变化规律；二是颗粒间的接触特性，该因素决定了单位面积上土颗粒的接触点数与其随颗粒堆积方式和应力状态的变化规律。

3.1 可变结构吸力初步表达式

基于Щукин[10]土的结构强度理论，文献[3]初步给出了可变结构吸力的计算表达式：

(1)

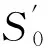
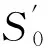
3.2 基于分形理论的可变结构吸力定量公式

(1)土颗粒粒度分布密度函数

土体是由一系列大小不等的土颗粒组成的，其颗粒组成可用分维理论中的分维系数来表征。土颗粒粒径分布的分维系数越大，说明土体中细颗粒的含量越高，粗颗粒含量则越低。

根据概率论，土体中颗粒半径大于r的概率与粒径、粒径的分布密度函数间满足以下关系[13]：

(2)

式中，r为土颗粒半径；D为土颗粒粒度分布的分维系数；P(r)为土体中颗粒粒径大于r的概率；p(r)为粒径的分布密度函数；k为比例系数。

对式(2)求导，即可得到颗粒粒径的分布密度函数，即：

p(r)=kDr-D-1

(3)

(2)土颗粒的分维系数

在颗粒粒径与颗粒累计含量间的对数关系曲线lgm(r)-lg(r)上做出分维直线，求出分维直线的斜率b，土颗粒粒度分布的分维系数可按下式确定[14～15]：

D=3-b

(4)

式中，b为lgm(r)-lg(r)双对数坐标中分维直线的斜率，可根据下式求得：

(5)

式中，lgm(r1)、lgm(r2)分别表示颗粒粒径大于r1、r2的累积含量。

(3)单位土体土颗粒总体积

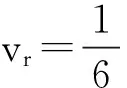
(6)

式(6)对r积分，可得单位体积土体中的土颗粒总体积：

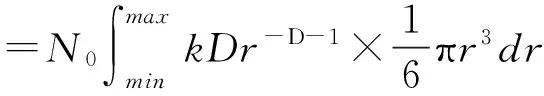
(7)

式中，rmax、rmin分别为土体中颗粒粒径的最大值和最小值。

(4)单位土体的颗粒总数

根据土力学中三相指标的换算关系，对于单位体积的土体，固体土颗粒的体积Vs可用下式表示：

Vs=1×(1-n)=1-n

(8)

式中，n为土体的孔隙率。

联合式(7)和式(8)，可以得到单位体积土体中的颗粒总数：

(9)

对于任意给定的土体，所有颗粒均大于或等于最小粒径，即颗粒大于最小粒径的概率为100%，即：

(10)

整理上式可得比例系数：

(11)

联合式(9)和式(11)式可得：

(12)

式中，各变量的含义同上。

(5)单位土体的接触点个数

颗粒的配位数Nc表征单个颗粒与周围其他颗粒的接触点数，配位数Nc跟土颗粒的堆积与排列方式有关。

对于单位体积的土体，定义土体内颗粒的接触点总数为Nj。由Nj的概念可知，Nj为单位体积土体内的土颗粒总数N0与配位数Nc的乘积，由于每个接触点均由两个颗粒共同拥有，所以单位体积土体内接触点总数可表示为：

(13)

(6)单位土体中土颗粒的总表面积

单个土颗粒的表面积Sr为：

Sr=πr2

(14)

单位体积土体中，p(r)dr×N0个粒径为r的颗粒表面积dSs为：

dSs=N0×p(r)dr×πr2

(15)

上式对颗粒半径r积分，可得单位体积土体中土颗粒的总表面积Ss为：

(16)

将式(11)代入上式可得：

(17)

式中，各变量的意义同上。

(7)单位面积土颗粒接触点数与宏观结构吸力

(18)

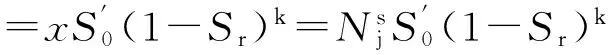
(19)

式中，各参数的物理意义同上。

土体的饱和度Sr、土颗粒比重G、孔隙比e、干密度ρd、及水的密度ρw间存在以下关系：

Sr=Gw/e

(20)

ρd=G×ρw/(1+e)

(21)

将式(4-3)代入式(4-2)，得：

(22)

式中，各参数的物理意义同上。式(22)给出了可变结构吸力与土体含水量、孔隙比、配位数、分维系数及颗粒半径之间的表达式。

4 可变结构吸力定量计算与分析

本文采用某场地的土样颗粒试验资料，根据试验结果，土体的最大粒径为 0.2 mm，即rmax=2×10-4m，然而，土体的最小粒径无法通过粒度分析试验测得，研究表明，颗径小于1.0×10-6m的土颗粒以胶体的形式存在于悬液中，因此，土颗粒的最小粒径取胶体颗粒粒径的上限，即rmin=1.0×10-6m。分维系数D根据粒度分析试验结果来确定[19]。

根据式(22)及表1可求得土体在不同含水量/饱和度、干密度及孔隙比条件下可变结构吸力的大小，计算结果见表2及表3，根据计算结果绘制可变结构吸力与含水量、干密度及孔隙比关系曲线，如图1～图3所示。

土样参数及计算结果 表1

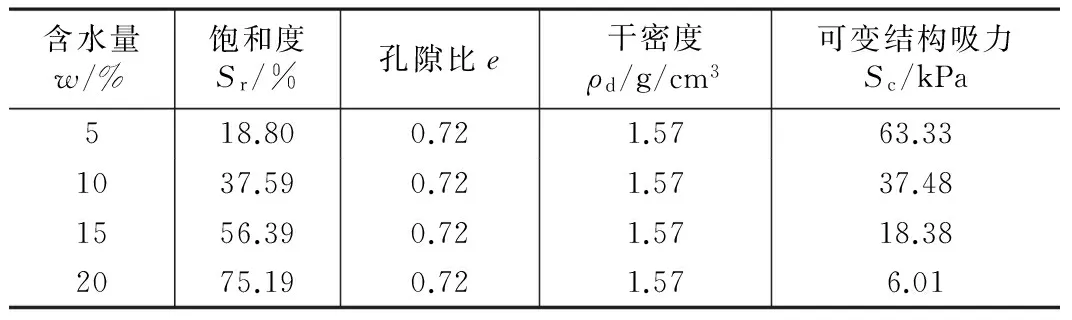
可变结构吸力与含水量定量关系 表2

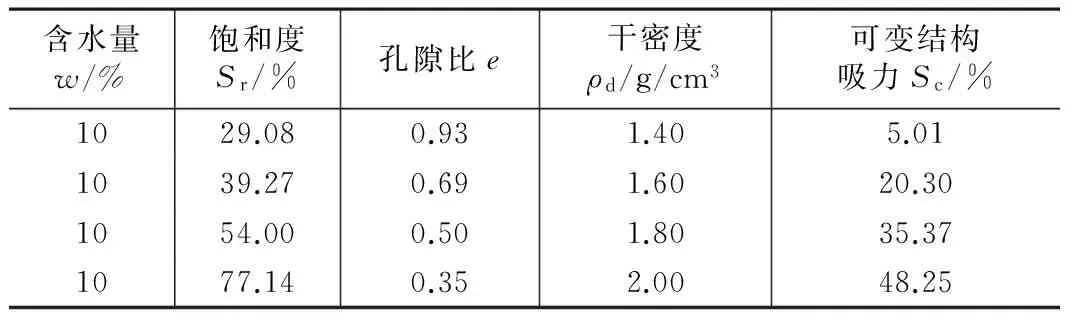
可变结构吸力与干密度、孔隙比定量关系 表3

图1 可变结构吸力与含水量关系曲线

图2 可变结构吸力与干密度关系曲线

图3 可变结构吸力与孔隙比关系曲线

由图可见，随着含水量的增大，可变结构吸力单调递减，当土体含水量增大至饱和时，即Sr=100%时，可变结构吸力趋向于0，从理论上分析，随着土体含水量的增大，水分在颗粒间的湿润作用增强，同时水分对颗粒间的胶结物溶解和稀释的作用也增强，胶结力作用减弱，因而导致可变结构吸力降低。

随着干密度的增大，可变结构吸力单调递增，从微观上分析，随着干密度的增大，单位体积土体内的土颗粒数和单位面积上的接触点数均增大，导致颗粒间咬合力、连锁作用等增强，因而导致土体的可变结构吸力增大。

随着孔隙比的增大，可变结构吸力单调递减，随着土体孔隙比的增大，相当于土体干密度减小，单位体积土体内的土颗粒数目减少，单位面积土体上的接触点数目随之减少，因而导致土体的可变结构吸力减小。

5 结 论

本文为研究不等粒径非饱和土结构吸力与非饱和土微观状态量(颗粒半径等)及宏观状态量(含水量等)之间的关系，借鉴了分形理论中的有关概念和方法、Horsfield六方紧密堆积模型，开展了公式推导及定量计算，主要研究内容和成果如下：

(1)基于文献[3]提出的可变结构吸力公式，进一步推导出不等粒径颗粒间可变结构吸力与与土体含水量、孔隙比、配位数、分维系数及颗粒半径之间的表达式；

(2)对可变结构吸力进行了定量计算，得出了以下结论：

①随着含水量的增大，可变结构吸力单调递减，当土体含水量增大至饱和时，即Sr=100%时，可变结构吸力趋向于0；

②随着干密度的增大，可变结构吸力单调递增；

③随着孔隙比的增大，可变结构吸力单调递减。

本文基于不等粒径球形颗粒模型，假设土颗粒按Horsfield模型堆积，从理论上推导出非饱和土的可变结构吸力与含水量、干密度及孔隙比间的定量计算表达式，与文献[3]的理论研究及文献[12]的试验研究结果一致。然而，对不等粒径、任意堆积甚至颗粒形状不规则的实际土体，有待进一步研究。

[1] Fredlund D G，Rahadjo H. Soil mechanics for unsaturated soils[M]. NewYork：John Wiley and Sons，1993.

[2] 汤连生，王思敬. 湿吸力及非饱和土的有效应力原理探讨[J]. 岩土工程学报，2000，22(1)：83～88.

[3] 汤连生. 结构吸力及非饱和土的总有效应力原理探讨[J]. 中山大学学报，2000，39(6)：95～100.

[4] 汤连生. 从粒间吸力特性再认识非饱和土的抗剪强度理论[J]. 岩土工程学报，2001，23(4)：412～41.

[5] 汤连生，颜波，张鹏程等. 非饱和土中有效应力及有关概念的解说与辨析[J]. 岩土工程学报，2006，28(2)：216～220.

[6] Bishop.A.W.The principal of effective stresses lecture delivered in Oslo，Norway，1955，printed in Teknisk，Ukblad，1959，106(39)：859～863.

[7] Bishop.A.W.，Blight G.E．Some aspects of effective stress in saturated and partially saturated soils[J]. Geotechnique，1963，13(3)：177～197.

[8] Fredlund.D. G and Morgenstern.N.R. Stress state variables for unsaturated soils[J]. Journal of the Geotechnical Engineering Division，Proceedings，ASCE (GTS)，1977，103：447～466.

[9] Fredlund.D. G，Xing.A.，Barbour.S.L. The relationship of the unsaturated soil shear strength to the soil-water characteristic curve[J]. Can. Geotech. J. 1995，32： 440～448.

[10] Frediund.D.G Bringing unsaturated soil mechanics into engineering practice. Proc. of 2nd International Conference on Unsaturated Soils[J]. Beijing，1998(2)：1～36.

[11] 邓钟尉.基于三轴试验的非饱和土抗剪强度影响因素分析[J]. 城市勘测，2014(6)：164～168.

[12] 李留仁，赵艳艳，李忠兴等. 多孔介质微观孔隙结构分形特征及分形系数的意义[J]. 石油大学学报·自然科学版，2004，28(3)：105～107.

[13] 刘松玉，方磊，陈浩东. 论我国特殊土粒度分布的分形结构[J]. 岩土工程学报，1993，15(1)：23～30.

[14] 徐永福，田美存. 土的分形微结构[J]. 水利水电科技进展，1996，16(1)：25～29.

[15] 徐永福，刘斯宏，董平. 粒状土体的结构模型[J]. 岩土力学，2001，(4)：367～372.

[16] 慕青松，马崇武，苗天德. 低含水率非饱和砂土抗剪强度研究[J]. 岩土工程学报，2004，26(5)：674～678.

[17] 张鹏程. 基于湿吸力和结构吸力的非饱和土抗剪强度理论及研究[D]. 广州：中山大学，2012.

[18] 奥细波夫. 黏土类土和岩石的强度与变形性能的本质[M]. 李生林，张之一译. 北京：地质出版社，1985：137～148.

[19] 江龙. 胶体化学概论[M]. 北京： 科学出版社，2004：4～7.

[20] M. E . Fayed ，L . Otten，粉体工程手册[M]. 北京：化学工业出版社，1982.

Quantitative Calculation on Structure Suction of Unsaturated Soil Based on Fractal Theory

Deng Zhongwei

(Guangzhou Urban Planning Survey and Design Institute，Guangzhou 510060，China)

Existing research shows that strength and deformation characteristics of unsaturated soil are largely determined by structure suction. Based on preliminary expressions of variable structure suction，by using concepts and methods of fractal theory for reference，derive quantitative formula derivation on variable structure suction with water content，dry density and void ratio of unsaturated soil with unequal particle diameters. The results show that the variable structure suction monotonically decreases with water content，increases with the dry density and void ratio，consistent with previous theoretical studies and experimental research results.

unsaturated soil；fractal theory；structure suction；unequal particle diameters；water content

1672-8262(2017)04-163-05

TU442

A

2016—08—30

邓钟尉(1986—)，男，硕士，工程师，主要从事工程地质、水文地质勘察、基坑支护设计以及地质灾害防治方面的生产和科研工作。