《信号分析与处理》教学理论框架建立

邬世英

(长江大学地球物理与石油资源学院，湖北 武汉 430100)

《信号分析与处理》教学理论框架建立

邬世英

(长江大学地球物理与石油资源学院，湖北 武汉 430100)

《信号分析与处理》是勘察技术与工程专业一门重要的基础课程，涉及的内容抽象、公式繁多，理论分析与实际应用结合困难。根据该课程多年的讲授经验，并结合学生反馈的接受情况，阐述了《信号分析与处理》理论框架建立的必要性，重点提出了该课程的2个理论框架——基于抽样定理的理论框架和正交变换的理论框架，并以该课程的主要知识点为例，详细讲解了基于2个理论框架的各知识点的关系梳理。

信号分析与处理；理论框架；抽样定理；正交变换

勘查技术与工程专业的《信号分析与处理》课程，其主要内容是将《信号与系统》和《数字信号处理》2本书的内容结合起来，涉及的课程内容多、公式多、定义多、推导多，知识点容易混淆，学生普遍反映学习难度大。

笔者通过多年的教学实践，充分认识到《信号分析与处理》是门具有思想性、方法性的课程，要做到课程教学系统性、条理性和易接受性，授课教师必须在授课过程中注重理论框架的建立，进而通过该理论框架系统地梳理整个课程的知识点，将各相关知识点有机地联系起来。通过建立理论框架，达到提纲挈领、总揽全局的效果。

在《信号分析与处理》课程中，需要建立怎样的理论框架呢？根据多年的教学实践，笔者以为该课程的理论框架主要是基于抽样定理和正交变换。

1 基于抽样定理的理论框架

在工程中的许多信号实际是连续时间信号，但是用计算机处理上述信号时，首先需要对连续信号进行抽样得到离散信号，离散信号和连续信号就是局部和整体的关系[1]。离散信号可以恢复为连续信号的条件就是时域抽样定理的内容，即：一个最高频率为fm的频带有限信号f(t)，在抽样频率fs≥2fm的条件下，可由它在均匀间隔点的抽样值进行唯一的确定[2]。

抽样定理是连续信号与离散信号的桥梁，通过抓住抽样定理这个理论基点，可以很好地将连续信号和离散信号的各个知识点、各种变化系统地进行梳理：①离散信号的频谱是连续信号频谱的周期延拓，延拓周期是抽样频率；②整个课程可以分为连续时间部分和离散时间部分，信号可以分成连续信号和离散信号，系统可以分成连续系统和离散系统；③针对连续信号的变换，有连续时间信号傅里叶级数分解(CTFS)、连续时间信号傅里叶变换(CTFT)、拉氏变换，针对离散信号的变换有离散时间信号傅里叶级数分解(DTFS)、离散时间信号傅里叶变换(DTFT)、离散傅里叶变换(DFT)、快速傅里叶变换(FFT)及Z变换。

有了抽样定理的桥梁作用，在连续时间信号傅里叶变换的基础上，很容易推导出离散时间信号的傅里叶变换公式，理解离散信号的频谱。这样，学生就可以轻松地从连续信号的傅里叶变换学习过渡到离散信号的傅里叶变换的学习，易于知晓上述各种变换的区别和联系。

图1(a)是连续非周期信号，其频谱也是连续非周期信号(图1(b))。通过抽样定理将连续非周期信号进行等间隔抽样得到离散时间信号(图1(c))，其傅里叶变换的频谱是连续周期信号(图1(d))。抽样定理指出，信号时域的抽样会导致频域的周期性。通过该结论就可以判断出离散信号频谱的特征是周期性的。

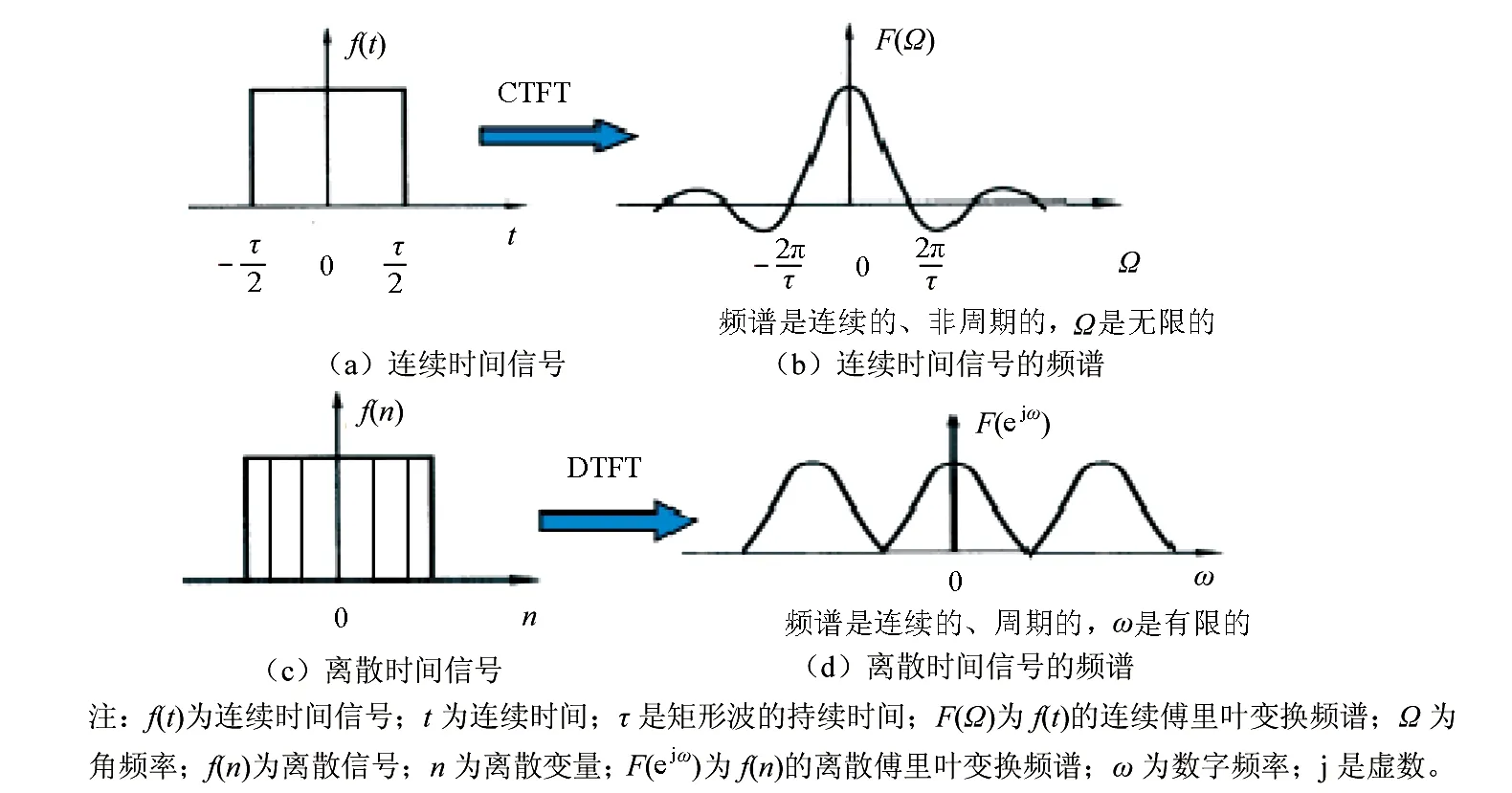
图1 CTFT和DTFT关系示意图

连续、离散时间信号的傅里叶变换的正、反变换公式为：

(1)

(2)

(3)

(4)

结合抽样定理，对比CTFT正、反变换式(1)、(2)与DTFT正、反变换式(3)、(4)之间的差异，可以发现，经过抽样后，t改为n，Ω改为ω，式(1)的积分形式变成了式(3)的累加形式，其他形式是一致的。

2 基于正交变换的理论框架

信号正交分解在信号系统理论中占有重要地位。信号的正交分解犹如矢量的正交分解，是把信号分解成一系列正交分量之和。进行信号的正交分解是先选一组正交基底(信号)，再找出待分解信号在各基底上的投影，从而将信号表示为各基底信号的加权线性组合。在处理信号时，由于信号的各分量正交，互不影响，处理得以简化[3]。在《信号分析与处理》课程中，涉及到的变换都属于正交变换，只是采用的正交基函数不同，导致变换的不同。因此，在讲解各种信号变换之前，提纲挈领地讲述信号的正交分解，使得后面的各种变换容易引出，从而使学生对各种变换有总体的认识，不会孤立地看待每种变换。

在具体的讲授过程中，首先讲解正交变换的理论、正交信号集的概念、正交的组合系数的推导；然后详细讲述课程中出现的所有正交信号集以及与该集相对应的组合系数。在正交变换章节的授课中，将课程中除了Z变换的其他变换的理论公式全部推导出来，在后续课程的讲解中，就不需要重新进行变换公式的推导，而且学生也易于接受，明白上述变换都是服从于正交变换这一基本原理。

《信号分析与处理》课程中用到的正交信号集主要有三角函数集、三角序列集、虚指数函数集和虚指数序列集。

三角函数集：

三角序列集：

虚指数函数集：

虚指数序列集：

式中：Ω0是基波频率；kΩ0是谐波频率；N为周期；k为频率域的自变量。

对于周期CTFS，采用三角函数集得到三角函数形式的傅里叶级数，采用虚指数函数集得到指数形式的傅里叶级数；对于周期DTFS，采用三角序列集得到三角函数形式的傅里叶级数，采用虚指数序列集得到指数形式的傅里叶级数；DFT采用的是虚指数序列集。

3 结语

通过将基于抽样定理和正交变换的2个理论框架应用到《信号分析与处理》课程教学中，可以很好地将课程的各个知识点和变换进行系统的梳理，使课程内容成为一介有机整体，让学生更易于掌握和学习。

[1]程乾生. 数字信号处理[M].北京：北京大学出版社，2010.

[2]张华清, 许信玉，赵志军. 信号与系统分析[M].北京：机械工业出版社，2006.

[3]吴京，果明明，徐忠富，等. 信号与系统分析[M].长沙：国防科技大学出版社，1999.

[编辑] 龚丹

2016-08-27

邬世英(1978-)，女，博士，讲师，主要从事地震信号处理的教学与研究工作，wushiyingok@163.com。

G642.0

A

1673-1409(2017)15-0040-03

[引著格式]邬世英.《信号分析与处理》教学理论框架建立[J].长江大学学报(自科版), 2017,14(15):40～42.