基于Intrinsic Time-scale Decomposition算法的扰动信号特征量提取问题研究
李 芹
(昆明轨道交通集团有限公司,云南 昆明 650000)
基于Intrinsic Time-scale Decomposition算法的扰动信号特征量提取问题研究
李 芹
(昆明轨道交通集团有限公司,云南 昆明 650000)
由于电能质量扰动信号具有非线性的特点,当下算法无法有效提取电能质量扰动信号,采取Intrinsic Time-scale Decomposition算法,可以有效提取电能质量扰动信号的频率、幅值、相位等特征量。利用Intrinsic Time-scale Decomposition算法提取电能质量扰动信号的Proper Rotation Component分量,后对Proper Rotation Component分量进行Hilbert变换以求得电能质量扰动信号的相位和瞬时频率,再根据电能质量扰动信号的高频突变点得到电能质量扰动信号的起止时间;根据envelope函数求得衰减因子。利用软件开发程序MATHEMATICA对电能质量扰动信号进行分析,结果表明,Intrinsic Time-scale Decomposition算法可以很好地提取电能质量扰动信号特征量,并且具有极佳的抗噪性能。
Intrinsic Time-scale Decomposition;扰动信号;故障分析
电网容易受到各种干扰信号的影响而致使本身的波形发生畸变,导致电能的质量出现严重的问题。而当下各种高质量电器设备的使用使得人们对于电能的质量有了更高的要求,故而,对于电能质量扰动信号的研究具有十分重要的现实意义[1-3]。
鉴于此,国内外学者对于电能质量扰动信号进行了大量的研究,其主要方法有:Fourier变化法、小波变换法[4]、Prony算法/改进Prony算法[5]、Hilbert-HuangTransform算法[6]、Mathematical Morphology算法[7]等。但这些算法都存在着自身无法克服的缺陷:Fourier变化法无法反映电能质量扰动信号的衰减阻尼特性,其分析精度受到数据的严重制约[7];小波变换法的抗噪能力较差,无法针对具有多重噪声的电能质量扰动信号的特征量进行有效地提取[8];Prony算法/改进Prony算法的计算速度较慢,计算结果受到噪声的严重影响,对于非线性问题的处理能力较弱[9];Hilbert-HuangTransform算法无法结算电能质量扰动信号的衰减因子,在计算瞬态参数时端点效应严重[10];Mathematical Morphology算法的结构元素的选取过度依赖经验,其普适性能较差[11]。Intrinsic Time-scale Decomposition算法是建立在Empirical Mode Decomposition和Local Mean Decomposition基础上的一种新兴自适应算法,可以将任意的复杂电能质量扰动信号分解为具有现实物理意义的Proper Rotation Component分量和误差余量/残余分量,计算速度快,抗噪性能强[12-14]。
基于Intrinsic Time-scale Decomposition算法的基本原理,结合电能质量扰动信号的相关特点,本文提出了一种新的电能质量扰动信号特征量的提取方法,思路如下:首先利用Intrinsic Time-scale Decomposition算法将电能质量扰动信号分解为若干现实物理意义的Proper Rotation Component分量和误差余量/残余分量,然后对Proper Rotation Component分量进行Hilbert变换以求取瞬时频率、相位。此后,利用envelope函数计算幅值、衰减因子。最后,利用软件开发程序MATHEMATICA对单一电能质量扰动信号和复合电能质量扰动信号进行分析,验证本文算法对于电能质量扰动信号特征量的提取问题的适用性和优越性。
1 Intrinsic Time-scale Decomposition算法简介
利用Intrinsic Time-scale Decomposition算法将电能质量扰动信号分解为若干现实物理意义的Proper Rotation Component分量和误差余量/残余分量的步骤如下:
1)寻找信号x(t)的极值x(k)以及对应的时刻t(k)。
Lk+1=αx(k)+[(tk+1-tk) /(tk+2-
tk)][x(k+2)-x(k)]+(1-α)x(k+1).
(1)
其中:k=1,2,3,…,M-2,M为信号x(t)的极值x(k)的个数;0<α<1,一般取α=0.5,所以Lk∈[L2,LM-1]。
2)对L1,LM进行估算,根据Empirical Mode Decomposition的端点延展的理论,用Mirror extension算法将左右极值点向两端延展,得到左右的极值点(t0,x0),(tM+1,xM+1),如果令k=0或者k=M-1,便可以得到L1,LM。
3)采用Rationalsplineinterpolation函数将L1,L2,…,LM进行拟合,便得到了基线信号βL1(t)。将基线信号βL1(t)从原始信号x(t)中分离,便可以得到
h1(t)=x0(t)-βL1(t).
(2)
其中,如果h1(t)为ProperRotationComponent分量,则输出h1(t);如果h1(t)不为ProperRotationComponent分量,则用h1(t)作为源信号,重复步骤1)至步骤3),直到h1(t)为ProperRotationComponent分量的时候循环结束,记作
PRC1=h1k(t).
(3)
4)将Proper Rotation Component分量PRC1(t)从原始信号x(t)中分离,得到
u1(t)=x0(t)- PRC1.
(4)
其中,u1(t)为剩余信号。
将剩余信号u1(t)作为原始信号,重复步骤1)至步骤4)共n-1次,直到un(t)为常函数或者单调函数。
2 提取扰动信号特征参数
对于任意的信号x(t),Hilbert变换y(t)为

(5)
根据式(6),x(t)和y(t)为共轭复对数,所以,解析信号z(t)为
z(t)=x(t)+jy(t)=|z|ejΦ(t).
(6)
相位函数为
Φ(t)=Imlnz(t).
(7)
式中,Im是虚部的意思。对式(7)求导便可以得到瞬时频率
f(t)=1/2π×dΦ(t)/dt=1/2π×
Im(1/z(t)×dz(t)/dt).
(8)
故而,幅值函数
α(t)=(x(t)2+y(t)2)0.5.
(9)
因为电能质量扰动信号可以表示为n个振荡模态的和,故而x(t)也可以写成

(10)
式中:Ai为振荡模态i的幅值;λi为振荡模态i的衰减因子;φi为振荡模态i的初始相位;ft为振荡模态i的频率;因为Proper Rotation Component分量和振荡模态是一一对应的,幅值函数α(t)可以认为是振荡模态的瞬时幅值。
αi(t)=Aieλi t.
(11)
故而,振荡模态i在时间j时刻的衰减因子λi,j可以表达为
λi,j=ln(αi,j/Ai)/jΔt.
(12)
式中:λi,j为振荡模态i在时间j时刻的瞬态幅值;Δt为间隔时间。为了进一步减小间隔时间Δt对最终计算结果的不利影响,λi,j可以表达为
λi,j=ln(αi,j/(αi,j1) )/Δt.
(13)
3 MATHEMATICA仿真验算
利用MATHEMATICA将Intrinsic Time-scale Decomposition算法进行程序化,并对电网中遇到的实际问题进行仿真验算。
3.1 电压暂降信号分析
x1(t)= {1-0.5[UnitStep(t-0.06)-
UnitStep(t-0.12) ] }sin(100πt+π/6).
(14)
式(14)是电压暂降信号的表达式,其中,UnitStep为单位跃阶函数,取频率f=3 200 Hz。MATHEMATICA仿真结果见图1。

图1 电压暂降信号分析结果
根据图1,电能质量扰动信号幅值发生了变化,而且可以辨识出电能质量扰动信号发生变化的时刻和突变频率,并提取扰动段内的特征参数(见表1~6)。

表1 初始时刻参数提取结果

续表1

表2 终止时刻参数提取结果

表3 频率提取结果

表4 幅值提取结果
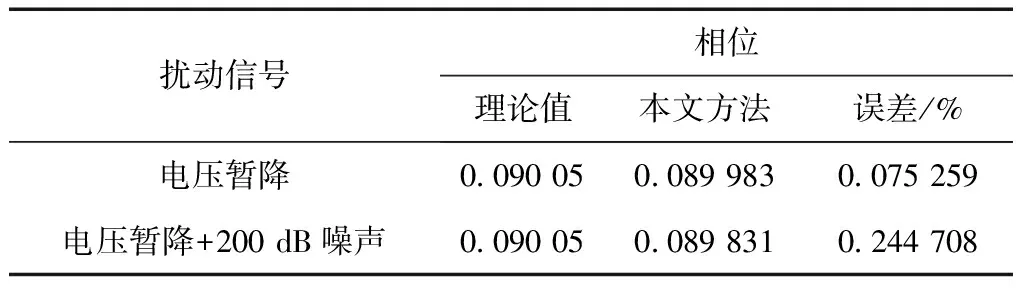
表5 相位提取结果

续表5

表6 衰减因子提取结果
根据表1~6可以看出,Intrinsic Time-scale Decomposition算法提取的电能扰动信号的特征参量具有极高的精度:最大误差不超过0.5%。在加入了20 dB噪声之后,Intrinsic Time-scale Decomposition算法与理论值的误差没有明显变化,说明Intrinsic Time-scale Decomposition算法具有极佳的抗噪能力。
3.2 谐波扰动分析
x2(t)=3sin(100πt+π/3)+2sin(300πt+π/3)
[UnitStep(t-0.02)-UnitStep(t-0.14) ]+
sin(700πt+π/4)[UnitStep(t-0.06)-
UnitStep(t-0.14) ].
(15)
式(15)是谐波扰动信号的表达式,其中,UnitStep为单位跃阶函数,取f=3 200 Hz。MATHEMATICA仿真结果见图2。
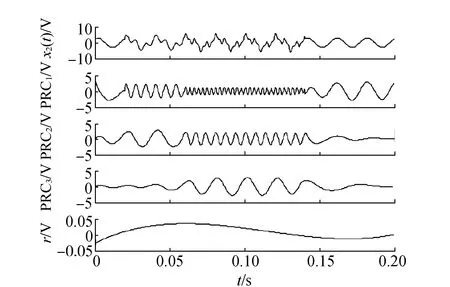
图2 谐波扰动信号分析结果
根据图2,PRC1出现了两种形态不同、发生时刻不同的谐波,但PRC2只是出现了一种类型的谐波。通过Intrinsic Time-scale Decomposition算法将PRC1、PRC2、PRC3依次分离,信号的频率逐渐降低,但每段信号的最高次的谐波都出现在PRC1中。为了进一步观察谐波的特性,计算PRC1、PRC2的瞬时频率(见图3)。

图3 PRC1、PRC2的瞬时频率
根据图3,时间t从0.021 32 s到0.062 39 s的区间内,PRC1的瞬时频率皆为151 Hz附近,PRC2的瞬时频率皆为50 Hz附近。但从0.062 39 s到0.141 5 s,PRC1的瞬时频率增加到350 Hz附近, PRC2的瞬时频率增加到151 Hz附近。其余时刻,PRC1的瞬时频率为基波,而PRC2的瞬时频率为0。时间t从0.021 32 s到0.062 39 s的区间内,信号有3次谐波,但时间t从0.062 39 s到0.141 5 s的区间内,信号有3次、7次谐波,与数学模型一致。Intrinsic Time-scale Decomposition算法计算得到的瞬态幅值和瞬态频率列于表1。
3.3 衰减振荡分析
x3(t)=5sin(100πt+π/3)+
2.5e^100tsin(1 000πt+π/6)[UnitStep(t-
0.04)-UnitStep(t-0.16) ].
(16)
式(16)是衰减振荡扰动信号的表达式,其中,UnitStep为单位跃阶函数,取f=3 200 Hz。MATHEMATICA仿真结果见图4。

图4 谐波扰动信号分析结果
根据图4,PRC1包含衰减振荡分量和基波分量,但是PRC2只含有基波分量,Intrinsic Time-scale Decomposition算法将高频分解为低频,这也是Intrinsic Time-scale Decomposition算法的一大优势。从图中提取扰动发生的起止时刻,利用Intrinsic Time-scale Decomposition算法计算衰减振荡参数(见表1)。
3.4 电压闪变分析
x4(t)=cos(2πft) {1+0.1[UnitStep(t-0.2)-
UnitStep(t-2) ][cos(6πt+π/3)+
0.3cos(30πt) ] }.
(17)
式(17)是衰减振荡扰动信号的表达式,其中,UnitStep为单位跃阶函数,取f=3 200 Hz。MATHEMATICA仿真结果见图5。

图5 电压闪变信号分析结果
根据图5,从图中提取扰动发生的起止时刻,利用Intrinsic Time-scale Decomposition算法计算电压闪变参数(见表1)。
4 结 论
本文利用Intrinsic Time-scale Decomposition算法,针对电能质量扰动信号的特征量进行研究,提出了一种新型算法来计算电能质量扰动信号特征量的幅值、频率、相位等参数,结论如下:
1)针对Proper Rotation Component分量进行Hilbert变换,可以确定扰动发生的起止时刻,避免了传统方法计算扰动发生的起止时刻误差大的缺陷。
2)通过扰动段的Proper Rotation Component分量可以计算出相位、频率、幅值、衰减因子等参量,与理论值进行比较,误差都不超过0.5%。
[1] 张逸, 林焱, 吴丹岳. 电能质量监测系统研究现状及发展趋势[J]. 电力系统保护与控制, 2015, 43(2):138-147.
[2] 肖助力, 龚仁喜, 陈双, 等. 基于改进S 变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2015, 43(3):84-90.
[3] 肖助力, 龚仁喜, 陈双. 一种改进不完全S 变换的电压暂降检测方法[J]. 电力系统保护与控制, 2015, 43(9):62-68.
[4] KUMAR R, SINGH B, SHAHANI D T. Symmetrical Components Based Modified Technique for Power Quality Disturbances Detection and Classification[J]. IEEE Transactions on Industry Applications, 2016:1-1.
[5] ISLAM M M, HOSSAIN M R, DOUGAL R A, et al. Analysis of real-world power quality disturbances employing time-frequency distribution[C]// Clemson University Power Systems Conference. IEEE, 2016.
[6] GENG Chao, WANG Feng-hua, HUANG Rong-hui, et al. Harmonic Detection of Electrified Railway Based on Improved Hilbert-Huang Transform Method[J]. Journal of Shanghai Jiaotong University, 2014, 48(9):1225-1230.
[7] BIBILONI P, GONZLEZ-HIDALGO M, MASSANET S, et al. Mayor-Torrens t-norms in the Fuzzy Mathematical Morphology and Their Applications[M]Fuzzy Logic and Information Fusion. Springer International Publishing, 2016.
[8] XIAO F. Power Quality Disturbance Classification Method Based on Wavelet Transform and SVM Multi-class Algorithms[J]. Energy & Power Engineering, 2013, 5(4):561-565.
[9] HUANG Nantian, LU Guobo, CAI Guowei, et al. Feature Selection of Power Quality Disturbance Signals with an Entropy-Importance-Based Random Forest [J]. Entropy, 2016, 18(2).
[10] PENG L I, GAO J, DUO X U, et al. Hilbert-Huang transform with adaptive waveform matching extension and its application in power quality disturbance detection for microgrid [J]. Journal of Modern Power Systems & Clean Energy, 2016, 4(1):19-27.
[11] LING L, ZHENG X U. Mathematical Morphology Based Detection and Classification of Dynamic Power Quality Disturbances [J]. Power System Technology, 2006, 30(5):62-66.
[12] RESTREPO J M, VENKATARAMANI S, COMEAU D, et al. Defining a trend for time series using the intrinsic time-scale decomposition[J]. New Journal of Physics, 2014, 16(16):85004-85031(28).
[13] FENG Zhipeng, LIN Xuefeng, ZUO Ming J. Joint amplitude and frequency demodulation analysis based on intrinsic time-scale decomposition for planetary gearbox fault diagnosis [J]. Mechanical Systems & Signal Processing, 2016, 72:223-240.
[14] HOU T Y, SHI Z. Sparse time-frequency decomposition based on dictionary adaptation [J]. Philosophical Transactions of the Royal Society A-Mathematical Physical and Engineering Sciences, 2016, 374(2065).
[责任编辑:刘文霞]
Extraction problem on the disturbance signal feature based on Intrinsic Time-scale Decomposition algorithm
LI Qin
(Kunming Rail Transportation Group Co.,Ltd.,Kunming 650000,China)
As the power quality disturbance signal is characterized with nonlinear characteristics, the current algorithms can not effectively extract power quality disturbance signal. Herein, the Intrinsic Time-scale Decomposition algorithm (Intrinsic Time-scale Decomposition algorithm), can effectively extract power quality disturbance signal frequency, amplitude and phase characteristics of the volume. First, Intrinsic Time-scale Decomposition algorithm is used to extract power quality disturbance signal Proper Rotation Component component. Then, the Proper Rotation Component Hilbert transform components are proposed to achieve power quality disturbances phase and instantaneous frequency of the signal. Finally, the high-frequency mutation point power quality disturbance signal obtained power quality disturbance signal the beginning and end time; envelope function determined according to the attenuation factor. Use software program MATHEMATICA development of power quality disturbance signal analysis, the results showed that Intrinsic Time-scale Decomposition algorithm can extract the signal features of power quality disturbances, and has excellent anti-noise performance.
Intrinsic Time-scale Decomposition; perturbation signal; failure analysis
2017-01-06
李 芹(1985-),女,工程师,研究方向:电能信号分析.
10.19352/j.cnki.issn1671-4679.2017.04.011
TM76
A
1671-4679(2017)04-0047-05

