用矩阵法求数列通项公式
辽宁省黑山县第一高级中学数学组(121400) 刘大鹏
用矩阵法求数列通项公式
辽宁省黑山县第一高级中学数学组(121400) 刘大鹏
选修系列4中的《矩阵与变换》已经成为了有些省份的高考内容.罗增儒教授在文[1]中提到了常见的数列的通项能统一为用二阶矩阵的方幂来求解.这引起了笔者浓厚的兴趣,经过查阅文献并仔细研究,感觉用矩阵法求数列通项公式不但方法简便易懂而且有很强的规律性.现整理成文,供同行参考.
一.数列{an},已知a1,a2,an+2=aan+1+ban,n∈N∗型问题
1.矩阵及其方幂的引入
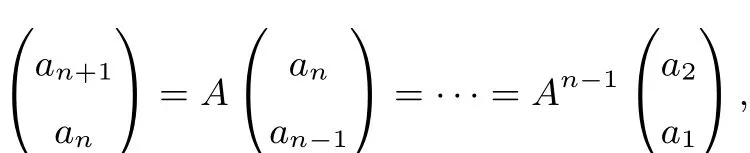
所以只需要求解An−1,即可求出{an}的通项公式.
2.用特征根理论求A的方幂

(其中E为单位矩阵).令f(λ)=0求得特征根λ1,λ2.
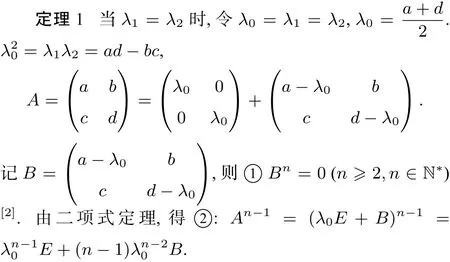
例1.(自编新题)已知数列{an},a1=1,a2=3,an+2=4an+1−4an,求{an}的通项公式.


例2.(自编新题)已知数列{an},a1=1,a2=3,an+2=3an+1−2an,求{an}的通项公式.

例3.(2009陕西文21)已知数列{an},a1=1,a2=2,(1)略;(2)求{a}的通项公式.n


二.函数f(x)=已知数列an+1=f(an),n∈N∗型问题
1.矩阵及其方幂的引入

例4.(自编新题)数列{an}中,a1=2,an+1=


3.特征根不相等时解法示例
例5. (自编新题)数列{an}中,a1=1,an+1=求{a}的通项公式.n

例 6. (2008陕西理 22)数列 {an}中,的通项公式.(2)(3)略.


例7. (2010全国I卷理22)数列{an}中,a1=1,(1)求{b}的通项公式.(2)n略.

三.数列{an},已知a1,an+1=qan+d型问题
1.矩阵及其方幂的引入
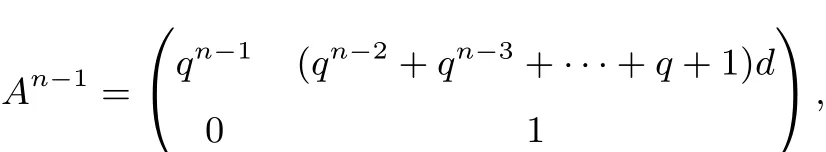
(n∈N,n≥2).所以

例8. (2014全国新课标理II 17(I))数列{an}中,a1=1,an+1=3an+1.求{an}的通项公式.

所以
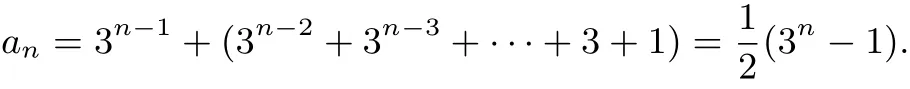
例9. (2007全国II理21)数列{an}中,a1∈(0,1),n∈N∗.(1)求{an}的通项公式;(2)略.

例10. (根据2012广东理19改编)已知数列{an}.a1=1,an+1=3an+2n.求{an}的通项公式.

所以an=3n−2n.
[1]罗增儒.谈中学教师的数学研究工作[J].中学数学教学参考,1997,(7).
[2]陈唐明.矩阵法求递推数列通项公式再探[J].高中数学教与学,2010(9).
[3]吕效国.分式线性递推数列通项的矩阵求法[J].南通工学院学报,1998(4).

