黑钙土不同土层在两种材质负压渗水器下的吸渗特性①

丁亚会，龙怀玉*，王 鹏，蒋雨州，方珍娟



黑钙土不同土层在两种材质负压渗水器下的吸渗特性①

丁亚会1，龙怀玉1*，王 鹏2，蒋雨州2，方珍娟3

(1 中国农业科学院农业资源与农业区划研究所，北京 100081； 2 黑龙江八一农垦大学，黑龙江大庆 163319；3长江大学生命科学院，湖北荆州 434025)

基于–5 kPa负压灌水条件下的一维垂直水分吸渗试验，分析了陶土和聚乙烯醇缩甲醛泡沫塑料(PVFM)两种材质负压渗水器在黑钙土A、B层的渗水性能，测定累计吸渗量、吸渗率、湿润峰及土壤含水率等指标，并利用它们考察了Kostiakov，Horton、Philip 3种常用的土壤水分吸渗模型及垂直一维非饱和土壤水分运动代数模式描述负压吸渗过程的适用性，进一步比较了不同处理下的模型参数。结果表明：①–5 kPa灌水条件下，PVFM渗水器和陶土渗水器的累计吸渗量没有明显差异，前者能有效替代后者作为负压渗水器；②黑钙土B层土壤水分吸渗特性比A层差，同时间内累计吸渗量较少，吸渗率降低速度更快；③短时间负压灌溉条件下，不同土层的累计吸渗量与湿润峰、吸渗率与湿润峰倒数、湿润峰平方与时间均存在明显的线性关系；④负压灌溉后距离渗水器上下各15 cm范围内，土壤含水率维持于20% ~ 33% 范围内，变异系数均在10% 左右；⑤拟合结果表明，Kostiakov与Philip模型能很好地描述–5 kPa负压灌溉下不同处理的水分吸渗特性，而Horton模型描述黑钙土A、B层较长时间的吸渗效果较差。

土壤层次；渗水器；负压灌溉；渗水性能；吸渗模型

入渗是指水分进入土壤的过程，是田间水循环中降水与灌水转化为土壤水分的重要环节，水分吸渗特性直接影响灌溉效率和灌溉质量。目前，水分入渗的相关研究多是基于农业生产和应用中的常规灌溉方式如微、喷、滴灌等正水头或零水头供水，而这会导致部分土体水分饱和、干湿交替、旱涝胁迫等不良后果。相比而言，负压灌溉使水分在土壤中呈非饱和态运动，是在基质势驱动下的水分运动，其入渗运动是一种吸渗运动，土壤内部水气条件更为协调，具有大幅度提高作物生产力的潜力[1]。因此，研究负压灌水条件下的土壤水分吸渗特性具有十分重要的意义。

对于负压灌水条件下的土壤水分吸渗特性已有一些相关的研究报道。范军亮和张富仓[2]在3种土壤上进行不同负水头的土壤水分吸渗试验，并基于Brooks-Corey 模型，结合非饱和土壤动力学方程，推导分析了各吸渗参数间的理论关系，验证了Philip 入渗公式在负水头条件下的适用性；梁锦陶等[3]通过室内模拟试验研究了黏壤土与砂土和供水水头对负压灌溉湿润峰动态变化和累计吸渗量的影响；辛琛等[4]基于黄绵土、红胶土与黑垆土的一维水平吸渗试验，并根据Brooks-Corey 模型推求了描述负水头条件下土壤吸渗公式，并分析了各参量间的函数关系；上官玉铎等[5]对比分析了不同负水头高度下的土壤吸渗规律，并采用 3 种吸渗模型分析了吸渗特点。但是，以上研究所采用的土壤均采自剖面上的某个层次或者不同层次的混合土壤，缺乏对土壤剖面不同层次吸渗特性的深入研究；而实际田间的吸渗往往是在具有明显层次的剖面上发生的，因而研究同一土壤不同层次间(尤其以根系分布较多的A、B土层更为重要)的吸渗特性对指导实际农田灌水具有更大价值。

负压渗水器是连接负压灌溉系统与土壤的媒介，也是决定负压灌水连续性和均匀性的重要因素，寻找性能优良的负压渗水器是研究与推广负压灌溉的重要环节。目前，试验中常用的渗水器多为陶土头与陶瓷盘[6-9]，但存在着韧性脆、易堵塞、重复使用率低等诸多问题。江培福等[10]曾使用纤维渗水器与陶土渗水器进行对比研究，但仅处于理论和实验室研究阶段；此后，丛萍等[11]研制出新型负压渗水器材料——出新型负渗水器，大大降低了渗水器制作成本。

综合考虑土层变化的吸渗差异性及渗水器因素，本研究拟定采用PVFM渗水器与传统陶土渗水器，基于黑钙土A、B层的土壤水分一维垂直吸渗试验，测定累计吸渗量、吸渗率、湿润峰及土壤含水率等指标，以此对比分析两种材质渗水器在不同土壤层次的一维垂直吸渗特性，并基于这些指标分析常用的Kostiakov、Horton、Philip入渗模型和土壤水分运动代数模式评价在负压吸渗运动上的适用性，以期进一步验证负压灌溉可行性和负压渗水器的可选性，为深入了解不同土壤层次的吸渗特性变化过程，发展基于负压灌溉的土壤水力参数和指导农田灌水提供一定的参考和依据。

1 材料与方法

1.1 供试负压渗水器

陶土头渗水器：由江苏宜兴工业陶瓷厂提供；PVFM渗水器：参照丛萍《聚乙烯醇缩甲醛负压渗水材料的制备及可行性分析》[11]。两种渗水器规格及发泡点如表1所示。

表1 不同材质渗水器的规格及发泡点

1.2 供试土壤

供试土壤取自黑龙江省大庆市肇州县的黑钙土A层和B层，土壤颗粒组成如表2所示，根据美国农业部土壤质地分类标准，供试土壤为壤质砂土。试验前将土样分别经碾压、粉碎、风干、过筛(2 mm)，备用。烘干法测得A、B层风干土样含水率分别为2.8% 和2.6%。试验时将黑钙土A、B层分别按照实际土壤体积质量(容重)1.17 g/cm3和1.34 g/cm3均匀装入土柱内。

表2 供试土壤的基本物理性质

注：土壤质地按照美国农业部制分类。

1.3 试验方案

如图1所示，试验设计采用高50 cm、宽30 cm、厚3 cm的有机玻璃土箱，以PVC塑料管将两种材质渗水器与作为负压水源的马氏瓶(标有刻度、直径10 cm)连接，装置连接完毕后检查其密封性。试验包括渗水器、土壤等两个因素，渗水器分为陶土渗水器和PVFM渗水器，土壤因素包括黑钙土A层、黑钙土B层，采用完全试验设计，共4个处理。试验时，将渗水器放入土箱中与土壤表面平齐，迅速填好土并开始计时，观测内容包括累计吸渗量、吸渗率、湿润峰运移和土壤含水率等参数。采用Microsoft Excel、Get Data、SAS8.0等软件进行数据采集、整理及统计分析。

2 结果与分析

2.1 不同渗水器下黑钙土的累计吸渗量与吸渗率

不同渗水器下，黑钙土累积吸渗量与吸渗率随时间的变化过程如图2所示。由图2A可以看出，累计吸渗量曲线在不同土层之间差异明显，黑钙土A层的累计吸渗量明显大于B层，而在不同渗水器之间差异不大。当使用陶土渗水器对黑钙土A层灌水时，3 300 min的累积吸渗量为7.6 ml，而B层为5.2 ml，A层比B层高出46.2%；用PVFM渗水器，相同时间内(3 300 min)黑钙土A层累计吸渗量为7.5 ml，而B层为4.9 ml，A层比B层高出53.1%。这表明其他因素相同时，土壤层次对负压灌溉累计吸渗量有明显的影响。从累计吸渗量的变化趋势来看，黑钙土A层的累计吸渗量曲线的斜率在试验时段内呈缓慢递减趋势，而B层在吸渗过程开始后不久，累计吸渗量曲线的斜率基本不变，说明黑钙土B层较A层能较早地达到稳定吸渗阶段，反映在2B图中尤为明显，这可能是由于黑钙土B层黏、粉粒含量较多、体积质量较大，相同负水头条件下的土壤水分吸渗特性变差所致。由图2b可以看出，–5 kPa灌水条件下两种材质渗水器所达到的稳定吸渗率相差不大，黑钙土A层的平均稳定吸渗率为0.001 4 cm/min，B层略低为0.001 1 cm/min。

2.2 不同渗水器下黑钙土各吸渗参数的相互关系

负压灌溉过程中，水分通过渗水器渗入至周围土壤，在基质势和重力势的作用下，向垂直和水平方向运动，逐渐润湿土壤并形成湿润峰。王全九等[13]曾利用垂直一维非饱和土壤水分运动的Darcy定理结合Parlange假定[14]和Brooks-Corey[15]模式分析了田间土壤水分运动特征，提出了一种预测预报土壤水分特征的新方法，具体形式为：

(2)

(3)

式中：为吸渗率，为累计吸渗量，z为湿润峰深度，θθθ分别表示饱和含水率、残留含水率和初始含水率；k为土壤表征饱和导水率，主要取决于土壤封闭空气对吸渗的影响程度；定义为土壤水分特征曲线和非饱和导水率综合形状系数式，定义为非饱和土壤吸力分配系数(1/cm)。

1) 累计吸渗量和湿润峰关系。从推导的湿润峰与累计吸渗量之间的理论关系式(2)可知，理论上累计吸渗量和湿润峰z之间呈线性关系。从图3中可以看出，两种材质渗水器在不同土层的湿润峰和累计吸渗量之间均为显著的线性关系，决定系数均在0.97以上。结合表3分析，相同累计吸渗量下，黑钙土A层中PVFM渗水器湿润峰运移距离略小于陶土渗水器，而B层两渗水器湿润峰运移无明显差别。比较不同土层湿润峰运移状况，发现相同累计吸渗量下黑钙土B层的湿润峰运移距离明显大于A层，说明相同土水势条件下A层土壤具有更高的非饱和土壤含水率。

2) 吸渗率与湿润峰倒数的关系。由推导的湿润峰与吸渗率之间的理论关系式(1)可知，吸渗率和湿润峰z倒数之间呈线性关系。从图4可以看出，4个处理下吸渗率和湿润峰倒数均呈现出显著的线性关系，决定系数2在0.945 ~ 0.985。

3) 吸渗时间与湿润峰平方的关系。从Boltzmann表征的水分吸渗模型z2=2(为Boltzmann变量)式中可以看出，湿润峰的平方z2与吸渗时间呈线性关系，从图5可以看出两者表现为显著的线性关系，其拟合决定系数均超过了0.977。进一步比较发现，相同土层内两种渗水器的值有明显差异，且陶土渗水器大于PVFM渗水器，说明一定时间内，使用陶土渗水器时湿润峰运移快于使用PVFM渗水器；比较相同渗水器不同土层的值，显示两种渗水器A层值均大于B层，表明一定时间内，相同渗水器进行负压灌溉时A层湿润峰运移要大于B层。

综上可以看出，累计吸渗量、吸渗率、湿润峰及吸渗时间存在着较好的线性关系，这与前人的研究结果相同[16-17]。由于初始含水率较低，故取滞留含水率等于初始含水率，即θ=θ；则累计吸渗量与湿润峰拟合关系为：

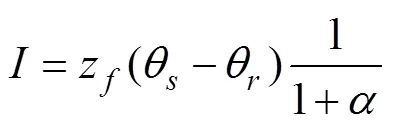
化简为，=kz(5)

根据式(5)对试验数据进行直线拟合计算得到、值，根据式(1)计算值，由此得到了–5 kPa灌水条件两种材质渗水器下黑钙土A、B层的拟合参数如表3。可以看出，两种材质渗水器在黑钙土A层水分吸渗拟合的值差异较大，而B层拟合值差异较小，说明不同材质渗水器在黑钙土A层拟合得到的土壤基质吸力与该吸力下导水率变化差异性较大；通过比较k值发现，使用陶土渗水器的土壤表征饱和导水率明显小于PVFM渗水器，说明使用陶土作为负压渗水器时，土壤封闭空气对吸渗影响较小；进一步比较值，发现–5 kPa灌水条件下不同土层及不同渗水器间的土壤吸力分配系数均有较大差异。

表3 土壤累计吸渗量、吸渗率及湿润峰拟合参数

注：为经验系数，定义为土壤水分特征曲线和相应吸力下导水率的综合形状系数式，定义为非饱和土壤吸力分配系数， k为土壤表征饱和导水率，12、22分别为和的拟合系数。

2.3 不同渗水器下黑钙土含水率分布状况

灌溉后的土壤含水率分布状况直接决定了灌水质量的优劣与否。常规灌溉与地下水补给方式下水势梯度差异导致了不同深度土壤含水率差异：常规灌溉下随土层深度的增加，土壤含水率减小，地下水补给方式则相反[18]，而负压灌溉正是二者的有机结合。图6显示了负压灌水后土壤含水率的分布状况，从图6中可以看出，在本试验的终止时刻，在距离负压渗水器上下各15 cm，土壤含水率维持在20% ~ 33% 范围内，且两种材质渗水器在不同土层的土壤含水率变化趋势相同，表现为土壤含水率随取样点与负压渗水器距离的增加呈现递减趋势，由此可保证作物根系有更大的土壤含水率，从而提高水分的吸收利用效率；同时由于重力势作用，渗水器下方土壤含水率变化幅度要小于上方。相同土壤层次，使用陶土渗水器进行灌水后的土壤含水率大于使用PVFM渗水器，其中土壤含水率最大差值出现在渗水器上方10 cm处，A、B层分别为1.9% 和1.8%。而渗水器下方土壤含水率差值呈现递增趋势，至15 cm处已达到2.7% 和2.5%；比较同种材质渗水器发现，黑钙土A层灌水后的土壤含水率大于B层同位置3% ~ 6%，这是由于黑钙土A层体积质量较小，可储存更多的土壤水分。土壤含水率变异系数能够在一定程度上反映灌水均匀度，这是检测和评判灌溉系统设计好坏的重要依据，也是进行系统管理的基础，还可以作为诊断系统设施完好与否的重要参考[16]。灌水后采集7个取样点的土壤(负压渗水器和上下方距离渗水器5、10和15 cm处)测量含水率，发现A层+陶土、A层+PVFM、B层+陶土、B层+PVFM 4种处理的含水率变异系数分别为10.5%、11.0%、9.3% 和10.6%，说明负压灌水后的土壤含水率变异系数相对较小，能有效控制渗水器湿润体的灌水均匀性，进一步验证了负压节水灌溉技术的可行性。该结果是基于未施肥条件下的室内模拟土柱试验得出的，而有研究指出长期施用有机肥会增加土壤水分含量波动性、砂层埋深对砂层土壤含水率分布有一定影响、气温与30 cm土层土壤含水率呈极显著负相关等[17-18]，因此有关不同生境下负压灌溉后的土壤含水率变化状况还有待进一步研究。

2.4 不同渗水器下黑钙土中3种入渗模型的适用性

Kostiakov[22]1932年在前苏联土壤上做了大量试验后提出吸渗公式：

=γt(6)

=γt1(7)

式中：是从0到时段的累计吸渗量，γ和为吸渗经验系数，可通过试验数据拟合求得。Kostiakov模型由于形式简单，计算方便，而应用比较广泛。

Horton[23]1933年在大量土壤吸渗试验基础上建立起来的经验吸渗模型，实用性较强，具体形式为：

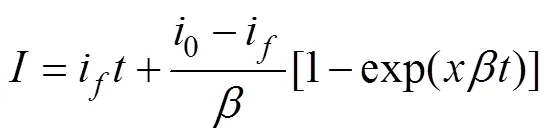
吸渗率形式为：

(9)

式中：为累计吸渗量，i是=0时的初始吸渗率，i是稳定吸渗率，是描述吸渗率降低速率的一个参数。

Philip[24]于1957年应用数值方法求解一定边界条件下均质多孔介质的吸渗问题解析了土壤水流的Richards方程，获得了Philip模型的最终之解，一般形式为：

(11)

式中：是从0到时段的累计吸渗量，为土壤吸渗率(cm/min0.5)，为稳定吸渗率，可通过吸渗试验测得。Philip模型有明确的物理意义，可由此推求土壤水分运动参数，便于建立其特征参数与土壤物理特征间参数，因而得以广泛应用。

3种吸渗模型都是基于表面土壤饱和条件下推求出来的，在负压灌水条件下是否同样适用不得而知。利用式(6)和(10)对累计吸渗量随时间变化过程的试验资料进行处理，得到两种吸渗模型的拟合参数列于表4中。结合图2分析表明，利用Kostiakov与Philip吸渗模型对–5 kPa下土壤累计吸渗量与时间及时间平方根进行相关分析得到的决定系数2均在0.99以上，说明Kostiakov和Philip吸渗模型均可以很好地描述负压灌水条件下的土壤水分吸渗过程。因此，此两种模型可较好预测相应灌溉条件下的累计吸渗量、吸渗率等，并可由此作为灌溉的基础参数。进一步分析表3可知，Philip模型中模拟黑钙土A、B层的稳定吸渗率没有明显差异，而吸渗率表现为A层显著大于B层，说明黑钙土B层持水保水能力比A层强，而土壤水分吸渗能力较弱，到达稳定吸渗阶段需要的时间相对较少，这与上面的分析结果一致。相同土层不同渗水器下PVFM渗水器吸渗率小于陶土渗水器，说明使用PVFM，毛管力对土壤中水分的吸收能力减弱[25]，分析原因可能PVFM孔隙结构对灌溉水的吸力大于陶土，从而导致土壤毛管吸力对水的吸渗效果减弱。

在Horton模型中是描述入渗率降低速率的一个参数，可以看出B层值明显大于A层，即B层吸渗率降低速率大于A层，同样说明黑钙土B层能够更短时间内达到稳定吸渗状态，这与上述分析结果一致；分析同一土层、不同渗水器下的值发现，A层没有显著差异，而B层值差异显著，表现为使用PVFM作为负压渗水器的值明显大于A层值，说明使用PVFM作为渗水器在黑钙土B层能够短时间内达到稳定吸渗状态。结合图7对比分析显示，Horton入渗模型不能准确、完整描述负压下土壤水分吸渗特性，可以看到Horton模型在预测黑钙土A、B层吸渗时有较大差异，表现为A层最拟合优度高于B层；但两种材质渗水器在黑钙土A层不同吸渗时期拟合程度又有较大差异，表现为前期拟合较好，以陶土渗水器为例相对误差达到了–5.5% 与–4.7%，而对于吸渗后期相对误差较大，最高误差达27.2%。综上可知，Horton模型不能准确描述较长时间的负压吸渗过程，这与前人研究结果一致[26]。

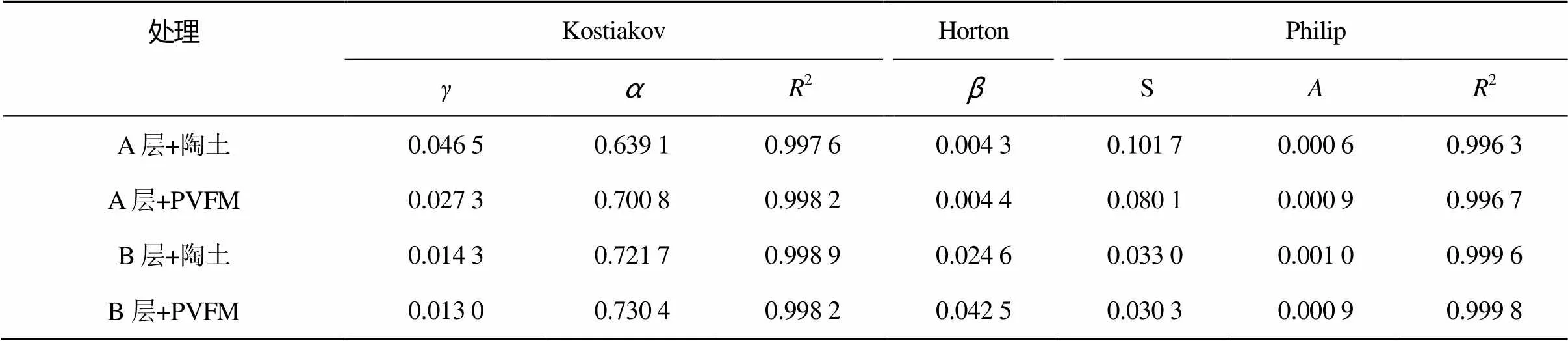
表4 3种吸渗模型的拟合参数

3 结论

1) –5 kPa灌水条件下，PVFM渗水器和陶土渗水器对黑钙土的累计吸渗量没有明显差异，前者能有效替代后者作为负压渗水器；黑钙土B层土壤水分吸渗特性比A层差，同时间内累计吸渗量较少、吸渗率降低速度更快；两种材质渗水器在不同土层的累计吸渗量与湿润峰、吸渗率与湿润峰倒数、湿润峰平方与吸渗时间均存在明显的线性关系；距离渗水器上下各15 cm范围内，土壤含水率维持在20% ~ 33%，且变异系数均在10% 左右。

2) 拟合结果表明，Kostiakov与Philip吸渗模型能较好描述–5 kPa负压灌溉下黑钙土A、B土层的水分吸渗过程，而Horton模型描述黑钙土A、B层较长时间的吸渗效果较差。

[1] 邹朝望, 薛绪掌, 张仁铎. 基于负水头下土壤水分一维水平运动理论与实验研究[J]. 土壤通报, 2006(5): 841–846

[2] 范军亮, 张富仓. 负水头条件下的土壤水分垂直一维入渗特性研究[J]. 土壤学报, 2010, 47(3): 415–421

[3] 梁锦陶, 孙西欢, 肖娟. 土壤质地和供水水头对负压灌溉土壤水分运移的影响研究[J]. 节水灌溉, 2011(6): 30–33

[4] 辛琛, 王全九, 樊军. 负水头条件下的水平一维土壤吸渗特征[J]. 农业工程学报, 2007, 23(9): 20–26

[5] 上官玉铎, 吕谋超, 宗洁,等. 负水头条件下入渗模型对于水分入渗规律适用性研究[J]. 节水灌溉, 2015(3): 8–11

[6] Ashrafi A D G M. Effect of soil texture on the emission characteristics of porous clay pipe for subsurface irrigation[J]. Irrig Sci, 2009(27): 201–208

[7] Siyal A A, Skaggs T H. Measured and simulated soil wetting patterns under porous clay pipesub-surface irrigation[J]. Agricultural Water Management, 2009 (96): 893–904

[8] 邹朝望, 薛绪掌, 张仁铎, 等. 负水头灌溉原理与装置[J]. 农业工程学报, 2007, 23(11): 17–22

[9] 李邵, 薛绪掌, 郭文善, 等. 负水头供水控水盆栽装置及灌溉系统的研究与应用[J]. 上海交通大学学报(农业科学版), 2008(5): 478–482

[10] 江培福, 雷廷武, Bralts Vincent F., 等. 土壤质地和灌水器材料对负压灌溉出水流量及土壤水运移的影响[J]. 农业工程学报, 2006, 22(4): 19–22

[11] 丛萍, 龙怀玉, 岳现录. PVFM渗水器规格对其负压渗水性能的影响[J]. 灌溉排水学报, 2015, 34(9): 7–14

[12] 丛萍, 龙怀玉, 岳现录, 等. 聚乙烯醇缩甲醛负压渗水材料的制备及可行性分析[J]. 高分子材料科学与工程, 2015, 31(10): 134–139

[13] 王全九, 邵明安, 郑纪勇. 土壤中水分运动与溶质迁移[M]. 北京: 中国水利水电出版社, 2007

[14] Parlange, J Y. Theory of water-movement in soils: 2. One-dimensional infiltration[J]. Soil Science, 1971, 111(3): 170–174

[15] Parlange J Y, Barry D A, Haverkamp R. Comment on ‘a simple approximate solution for horizontal infiltration in a Brooks-Corey medium’ by R. W. Zimmerman and G. S. Bodvarsson[J]. Transport in Porous Media, 1992, 9(3): 297–301

[16] 王全九, 王文焰, 吕殿青, 等. 水平一维土壤水分入渗特性分析[J]. 水利学报, 2000, 31(6): 34–38

[17] 郭向红, 孙西欢, 马娟娟, 等. 不同入渗水头条件下的Green-Ampt模型[J]. 农业工程学报, 2010, 26(3): 64–68

[18] 靳宇蓉, 鲁克斯, 李鹏, 等. 基于稳定同位素的土壤水分运动特征[J]. 土壤学报, 2015, 52(4): 792–801

[19] 宰松梅, 仵峰, 温季, 等. 大田地下滴灌土壤水分分布均匀度评价方法[J]. 农业工程学报, 2009, 25(12): 51–57

[20] 钱海燕, 陈玲, 孙波. 不同水文年气候和施肥对红壤剖面水分变化的相对影响[J]. 土壤, 2015, 47(2): 378–386

[21] 范严伟, 黄宁, 马孝义, 等. 应用HYDRUS_1D模拟砂质夹层土壤入渗特性[J]. 土壤, 2016, 48(1): 193–200

[22] Kostiakov A N. On the dynamics of the coefficient of water percolation in soils and on the necessity of studying it from dynamic point of view for purposes of amelioration[J]. Transactions of VIth International Congress Soil Science, 1932, 97(1): 17–21

[23] Horton R E. An approach towards a physical interpretation of infiltration capacity[J]. Soil Sci. Soc. AM. Proc., 1940, 5: 399–417

[24] Philip J R. The theory of infiltration：1.The infiltration equation and its solution[J]. Soil Sci, 1957, 83: 345–357

[25] 王全九, 张继红, 谭帅. 微咸水入渗下施加PAM土壤水盐运移特性研究[J]. 土壤学报, 2016, 53(4): 1056–1064

[26] 李雪转, 樊贵盛. 非充分供水土壤水分入渗模型的试验研究[J]. 灌溉排水学报, 2009, 28(4): 37–40

Infiltration Characteristics of Two Kinds of Negatively Pressurized Infiltration Devices in Different Layers of Chernozem

DING Yahui1, LONG Huaiyu1*, WANG Peng2, JIANG Yuzhou2, FANG Zhenjuan3

(1 Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing 100081, China;2 Heilongjiang Bayi Agricultural University, Daqing, Heilongjiang 163319, China; 3 Collge of Life Science, Yangtze University, Jingzhou, Hubei 434025, China)

Based on the vertical one-dimensional infiltration under the condition of –5 kPa, the water permeability of pot clay and PVFM in Chernozem zone A and zone B were analyzed. And the infiltration capacity, infiltration rate, humid peak and soil moisture content were measured and used to test the applicability of Kostiakov model, Horton model, Philip model and algebraic method of vertical one-dimensional unsaturated soil water movement in evaluating negative pressure infiltration, and further compared the model parameters under different treatments. The results indicate: 1) PVFM can replace pot clay as negative pressure infiltration device due to no significant difference in their measured accumulated infiltration; 2) Chernozem zone B has worse infiltration characteristics, less cumulative infiltration capacity and faster infiltration rate decrease compared with zone A in the same time; 3) In short time negative pressure irrigation, significant linear correlation exist between infiltration capacity and humid peak, between infiltration rate and reciprocal humid peak, between humid peak squared and time; 4) When using negative pressure irrigation, soil moisture contents within 15 cm up and down from infiltration device keep within 20%—33% with a variation coefficient of about 10%; 5) Fitting calculation proves that Kostiakov model and Philip model describe better the infiltration characteristics, while Horton model describes poorly in later period.

Different soil layers; Infiltration devices; Negatively pressurized infiltration；Infiltration property; Infiltration model

10.13758/j.cnki.tr.2017.04.024

S152.7

A

国家高技术研究发展计划项目(2013AA102901)资助。

(hylong@caas.ac.cn)

丁亚会(1990—)，男，山东济宁人，硕士研究生，主要从事农业节水技术研究。E-mail: dingyahui00@163.com