悬垂状海洋管线建模和分析方法综述

， ，

( 1.海洋石油工程股份有限公司， 天津 300461； 2.上海交通大学 a.海洋工程国家重点实验室，b.高新船舶与深海开发装备协同创新中心， 上海 200240； 3.天津修船技术研究所， 天津 300456)

悬垂状海洋管线建模和分析方法综述

王文伟1，张萌萌2a，2b，梁姝婷3

( 1.海洋石油工程股份有限公司，天津300461； 2.上海交通大学a.海洋工程国家重点实验室，b.高新船舶与深海开发装备协同创新中心，上海200240； 3.天津修船技术研究所，天津300456)

全面地阐述悬垂状管线常用的空间建模方法：悬链线法、非线性梁理论、弹性杆理论、集中质量法和多刚体理论；分析各方法的计算精度、效率和适用范围；分别针对悬垂状海洋管线在时间上离散的静力分析和动力响应分析，总结常用的数值算法，简单说明这些算法的优势和不足之处；对悬垂状海洋管线建模和分析方法的研究现状进行总结，并对今后的研究热点进行展望。

悬垂状管线；空间力学模型；静力分析；动力分析；综述

0 引 言

随着海洋油气工业的迅速发展，海底管道、立管、锚链在海洋油气开采和运输中的应用越来越广泛，悬垂状是其最常见的形态[1]。为预测悬垂状海洋管线的力学特性，保证管线的结构完整性，有必要对悬垂状管线进行建模分析计算。经过众多学者多年的研究，已形成多种管线分析技术。本文分别从空间和时间角度，详细说明管线的各种建模方法和数值分析方法，分析各方法的计算精度和效率，并指出优势和不足之处。

1 空间上离散方法

悬垂管线建模方法分类如图1所示。连续型建模通常用于悬垂管线的静力形态分析，离散型模型则可应用于复杂深水悬垂状管线静力、动力分析建模，能够考虑几何非线性、材料非线性及边界非线性等复杂问题。

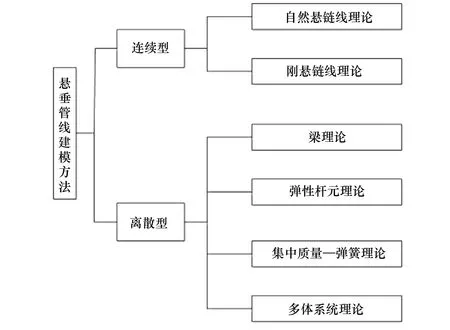
图1 悬垂管线建模方法分类图

悬垂状管线分析的第1步是根据要求选择合适的模型处理方法。在分析时，一般希望能够建立与实际工程结构完全一致的模型，但是悬垂状管线的分析，需要考虑非线性等复杂问题，建立完全贴合实际的模型非常困难。因而，通常需要在适当的范围内做一些假设，忽略边缘因素，抓住主要因素，建立力学模型。目前，学者们常用建模思想主要有悬链线思想和有限元思想。

1.1连续型建模方法

悬链线模型是一种有效的深水悬垂管线静力问题的求解方法。悬链线法将管线视为一条具有完全柔性、无延伸且均质的自由悬挂于2点的曲线，分为自然悬链线法和刚悬链线法。自然悬链线法理论简单易懂、结构形式简洁，可作为其他精细解法良好的起始点，但也存在一些不足：由于忽略管线弯曲刚度而导致的浅水区计算结果不够准确、触地点处弯矩不连续以及未能考虑管线所受的动载荷。水平力H下自然悬链线形态方程[1]为

该悬链线模型必须对悬垂管线非线性双曲方程进行线性化才可以求得闭合解。只有线性化的点附近是稳定的情况下解才是精确的，且无法求解水动力和缆索特性参数(如质量、弹性等)沿缆索改变的情况。

1967年，PLUNKETT[2]在已有自然悬链线法的基础上，考虑管线的弯曲刚度提出刚悬链线法，弥补了自然悬链线法的不足，但刚悬链线法依然无法进行管线动力响应分析。

目前，悬链线法已经广泛应用于锚链的设计、分析中。胡灵斌等[3]基于外力与系泊力平衡的思想，利用Excel软件求解符合水深和挂链力要求的最小抛锚距离；王丹等[4]编写VB程序，可在已知水深、风、浪、流等参数情况下，获得锚链的链长、重量以及最小抛锚距离等锚链参数，为单根锚链参数的选择提供方便。除此之外，谢文博等[5]采用该方法得到管线铺设过程中管线对船体的作用力，并分析作用力和管线形状随船体运动的变化规律。程闵等[6]利用自然悬链线理论，推导铺管作业回收管线时管线提升过程中提升角、最大提升高度和提升力的关系，以此为基础得到弃置回收管线作业时管线的基本边界条件。

1.2离散型建模方法

随着计算机技术和数值分析技术的发展，有限元思想越来越多地应用于管线模型处理中。根据离散后模型对质量/附加质量、弯曲、拉伸等物理参数的不同处理，大致分为以下几种模型：非线性梁模型、弹性杆模型、集中质量模型以及多刚体管线模型。

1.2.1 非线性梁理论模型

非线性梁理论将管线离散成梁单元微段，忽略管线截面变形的影响，仅考虑管线弯曲形变和轴向拉压。相比于悬链线思想，非线性梁理论在处理复杂边界条件和环境载荷时具有优势，且这种模型处理方法易于运用计算机语言进行数值计算。目前已有许多软件基于该方法进行管线建模和分析，例如Abaqus，RIFLEX等，这使得管线的相关分析更加方便。

BAI等[7]曾基于该理论，采用Abaqus有限元软件实现管线静态形态的求解，并在此基础上考虑波浪等环境载荷计算管线的动态响应。ZENG等[8]采用小应变、大变形的非线性梁模型模拟海洋立管铺设，对其进行静力分析，并在此基础上开发出名为“OPSA”的管线强度分析软件。该软件可以对立管(单层管、双层管)进行在位稳定性分析、VIV分析、铺设分析以及提管分析，具有较强的适用性。

但是随着水深的增加，管线/立管越来越长，采用非线性梁理论所需单元数越来越多，计算所需时间和占用的电脑内存随之增加，计算成本提高，效率降低。

1.2.2 弹性杆理论模型

弹性杆是极端细长且具有超大变形的细杆，不同于传统弹性力学的研究对象，弹性杆理论可以考虑管线剪切。该方法的优势在于可采用较大的单元，计算效率较高。

甄国强等[9]运用弹性杆理论建立铺设过程中海洋管线的二维综合相容的力学模型，考虑管线的几何非线性、边界非线性以及波、流等复杂环境载荷对管线的影响。KIM等[10]也采用弹性杆理论考虑系泊缆的变形和弹性伸长，研究系泊缆材料非线性对其张力和上部平台运动响应的影响。陈海飞[11]基于弹性杆理论在绝对坐标系下建立柔性立管的有限元模型，该模型考虑了几何非线性，且通用性强，可推广至锚链线、悬垂管线的分析中。

1.2.3 集中质量模型

集中质量模型将管道划分为有限数量的单元，每个单元由2个节点和1段无质量直线元组成，模型使用轴向伸缩阻尼弹簧、弯曲阻尼弹簧和扭转阻尼弹簧模拟轴向拉压、弯曲和扭转。相比于非线性梁理论，集中质量模型由于采用了集中质量矩阵，其分析计算时间明显减少，计算效率大大提高。

YING等[12]将该方法用于柔性悬垂立管的静力、动力分析中，并考虑水面波效应以及水面船舶运动对管线的影响。聂孟喜等[13]用二维集中质量法建立锚链和水鼓的数学模型，在时域内建立一种计算防风水鼓系泊系统系泊力的方法，解决了海洋工程中系泊系统在风、浪、流联合作用下系泊力的计算问题。

然而，由于集中质量模型整个管线运动仅是由多个通过弹簧连接的质点运动构成，柔性较大，因此当采用集中质量模型模拟浅水区刚性较大的管线时，计算精度较低。该方法适合柔性较大的海洋管线计算。

1.2.4 多刚体管线模型

多刚体管线模型将悬垂状管线离散为多个刚体单元，并假设刚体单元的质量集中在单元的质心上，每个单元通过可转动的节点连接，并以连接节点和单元的质心为对象建立运动方程。

JENSEN[14]基于多刚体系统思想，对考虑惯性力、流体阻尼力、恢复力、弯曲刚度以及海床影响的铺设管线进行二维动态分析；并采用新的系统模型思想对铺设中管线张力的变化进行分析，直接计算出管线张力的动态变化。MAREK[15]利用多刚体管线模型建立卷筒铺设海底管道分析模型，考虑材料非线性和几何大变形问题，重点分析2种不同的控制方式下不稳定的系统响应对铺管能力的限制。

多刚体管线模型的优势是计算速度快，可以满足较长的模拟时间要求，且该模型很好地解决了集中质量法在浅水区精度不高的问题。但是，由于采用离散的弯矩和质量，多刚体管线模型在计算精度上低于非线性梁和弹性杆理论模型。

自然悬链线法思想概念简单而且运算很快，是获得管线初始静力形态的首选方法，在悬垂状管线设计、分析的初期有着重要作用，但是无法处理复杂的载荷和边界。刚悬链线思想弥补了自然悬链线法在浅水区计算结果不准确的缺陷，但也无法处理管线的动力响应分析。在悬垂状管线建模和分析中有限元思想考虑了复杂边界、载荷对管线的影响，可以对管线动力响应进行分析。不同方法各有优缺点，分析时需根据实际情况，综合考虑计算效率和精度，选择最合适的建模方法。

2 时间上离散方法

在时间上，悬垂管线分析又有静力、动力之分。随着数值分析理论的发展，越来越多的数值分析方法应用到悬垂状海洋管线的静力、动力分析中。

2.1静力分析方法

对悬垂状管线进行静力分析的目的主要有2个方面：一是为动态分析提供较为精确的初始轮廓和相关参数；二是可对管线某些作业参数的敏感性进行分析。

悬垂状管线静力分析最简单的方法是自然悬链线法。但是，有时需考虑弯曲刚度和复杂边界条件等因素，这时就需要力学模型与数值解法相结合进行分析。

PLUNKETT[2]采用刚悬链线模型进行管线静力分析，应用渐近展开法获得方程精确解的一个近似值，且对于抗弯刚度很低的管线，可导出系列解。LI等[16]基于该方法开发相应的计算程序，分析不同参数对S型管线铺设中张紧器张力、管线极限铺设水深、管线弯矩和轴力的影响规律。该研究对管线铺设参数的选取有一定的参考价值。马锐[17]结合非线性梁模型与超松弛迭代法分析海底管道铺设悬垂状管线的力学特性，并进一步研究影响S型铺设和J型铺设管线应力的主要因素。徐德会[18]将非线性梁模型与加权残值法相结合，用于浅水和深水铺设中管线的静力分析，并在此基础上编制相应的计算软件，计算速度快，适用范围广。

众多学者在对锚链、立管进行静力分析时将不同力学模型与数值解法相结合进行分析：肖越等[19]采用有限差分法求解三维可弹性变形的锚链线模型，为锚链线动态分析提供初始轮廓形状。CHEN[20]采用大变形杆单元、非线性梁单元来离散锚链和钢悬链线立管模型，应用牛顿-拉斐逊法对控制方程进行迭代求解，扩大了GARRETT提出的Cable 3D程序的适用范围，提高了计算的稳定性和收敛速度。

当采用悬垂状管线静力分析的结果作为动态响应分析的前提时，研究人员往往选择形式简单、计算快速的自然悬链线法，使静力分析更加快捷、方便，兼顾精度。但是，当采用静力分析结果研究某些作业参数的敏感性或者对管线进行设计时，研究人员需考虑弯曲刚度、复杂边界等因素的影响使静力分析拥有较高精度，兼顾快捷、方便，一般采用各种有限元模型或者刚悬链线模型与数值解法相结合进行分析。

2.2动力响应分析方法

由于悬垂状海洋管线在实际作业中将受到复杂的海洋环境影响，管线应力、应变将会增大甚至产生屈曲。在对悬垂状管线进行设计、校核分析时，仅采用静力分析的结果将偏保守，需要对管线在海洋环境载荷作用下的动力响应进行分析。

目前，学者们对管线动力响应的研究主要集中在管线时域分析技术的应用上。时域分析技术非常适合模拟结构的几何非线性、载荷非线性和材料非线性。时域模拟计算时间长，但精确性高，在管线动力响应分析中的应用也越来越广泛。

典型的时域分析方法有：龙格-库塔法，Wilson法，Newmark法，广义-α法，等。这些方法大致可以分为显式算法和隐式算法两类。Wilson法、Newmark法、广义-α法属于隐式算法，而龙格-库塔法既存在显式格式也存在隐式格式。

2.2.1 龙格-库塔法

龙格-库塔法是基于泰勒展开所形成的单步法，可以自启动。该方法精度高，步长易于调节且计算稳定，因此是求解结构动力响应中常用的方法。

RAMAN-NAIR等[21]基于集中质量法建立三维柔性海洋管线的动力学模型，并采用龙格-库塔法求解动力学方程；POLLIO等[22]在此基础上对浮式系统管线/锚泊系统的非线性动力方程进行求解，主要通过Matlab编程实现，将4个特殊算例的龙格-库塔法编程计算结果与OrcaFlex和Newmark迭代法的计算结果进行比较，以确定程序的可行性和正确性。

龙格-库塔法的主要缺点是计算量较大，当所求解的光滑性较差时，计算精度可能不如低阶方法。除此之外，龙格-库塔法在处理高频轴向模态时条件稳定且时间步长小。因此，该方法更适合处理高加载速率问题，例如模拟管线的破坏和碰撞。

2.2.2 Newmark法

Newmark法是Newmark于1959年提出的，他引入了如下的速度和位移关系：

在海洋工程中，大部分学者都采用Newmark-β法来整合时间上的控制方程。这种方法绝对稳定、周期延伸低、零振幅衰减、精确性好、实施简单。

孟丹等[23]在对外部顺流作用下的钢悬链线立管动力响应进行分析时，采用Newmark-β法对动力学方程进行求解，基于Hamilton原理和拉格朗日应变理论，建立立管大变形动力学模型的详细推导过程，并给出了模型验证。童波等[24]对半潜式平台悬链线式系泊系统进行动力学分析，考虑系统间的相互耦合和非线性影响，采用Newmark-β法求解系统非线性动力方程。

2.2.3 Wilson法

Wilson法是在Newmark法的特例——线性加速度法的基础上，引入参数θ对加速度进行修正的隐式算法。该方法首先假设加速度在t至t+θΔt内线性变化，计算加速度在该区间内的近似解，而仅选择t至t+Δt内的解作为正式的近似解。

YING 等[12]结合集中质量法和Wilson法对悬垂管线进行时域分析，将时域分析结果与OrcaFlex软件计算结果对比，发现两者吻合度较高，证明该方法计算的可行性。

Wilson法的优势主要是，当参数θ值在1.37以上时该方法是无条件稳定的，可以选取较大的时间步长。这使得该方法比较适用于处理管线分析中周期相对较长的典型恒稳态响应问题。

2.2.4 广义-α法

广义-α法是在Newmark法的基础上引入参数α来调整运动方程位移项的一种无条件稳定算法。参数α作为可控的人工阻尼，可提高该方法的计算精度。同时，通过调整参数α可以使得算法在高频段具有其所需的数值阻尼，对高频段存在有效的衰减，而对低频段的影响较小。

GOBAT等[25]将该方法应用于锚链动力学方程的时间积分求解上，同时指出其他方法存在缺少数值耗散和受Crank-Nicholson干扰影响这2个问题，导致时间积分的稳定性存在潜在不确定因素。因此，增加数值耗散以期在处理高频数值响应时拥有二阶精度。为了让该方法在处理非线性问题时同样拥有较快的速度和计算稳定性，GOBAT等[26]于2006年提出一种自适应时间步选择、自适应网格和自适应松弛方法，同时将该方法扩展到深水系泊系统的分析上，并将计算结果与其他数值算法结果进行比较，验证了该方法的可行性。

2.2.5 其他数值算法

除了上文提到的方法外，还有一些数值算法被应用于管线动力响应问题的计算中。例如，在处理柔性多体系统动力学时易获得刚性较大的非线性动力学方程，由于该方程中既含有大的刚体运动变量，又包含小的弹性运动变量，给数值计算带来了很大的困难。上文所提到的显式算法大多是条件稳定的，不适合求解该类方程；隐式算法虽然是无条件稳定的，但是也存在潜在的计算风险。针对这类方程，常用的解法有Gear法、隐式龙格-库塔法、并行Rosenbrock法以及精细时程积分法等。JENSEN[14]将多刚体管线模型与Gear法相结合用于求解悬垂状管线的动态响应。MAREK[15]将其扩展到海底管道卷筒铺设的动力分析中。Matlab中也使用Gear法求解刚性微分方程。

目前，计算数学研究者们在已有方法的基础上提出很多改进的方法，例如精细积分法、时间域离散法等。这些方法在数值耗散、计算精度等方面有一定的优势，正逐渐应用于悬垂状管线动力响应的计算分析中，而Newmark法、Wilson法、广义-α法等由于理论相对简单、易于计算且能够满足精度要求，依然是学者们使用较多的方法。

3 总结及展望

悬垂状海洋管线是海洋工程中一种常见的结构形态，众多学者对其建模和分析提出了不同的方法，大致可总结如下：

(1) 对于悬垂状海洋管线的静力分析，选择自然悬链线法理论简单且计算方便；当考虑弯曲刚度或计算精度时，则可以采用刚悬链线法以及非线性梁等有限元方法，并结合摄动法、样条函数等数值方法求解。

(2) 悬垂状管线的动力响应分析往往涉及非线性内容，目前只能采用各种有限元方法结合数值解法进行悬垂状海洋管线的动力响应分析。在有限元方法中，非线性梁理论模型和弹性杆理论模型的计算结果精度较好，而集中质量法和多刚体管线模型精度较差，但是计算效率较高，且随着水深的增加该优势越明显。各种数值算法，只需根据模型运动方程简化结果的不同进行选择。

管线作业期间的安全性和完整性分析将是未来研究中的热点和难点，包括管线的涡激振动、屈曲、焊缝疲劳等复杂的结构分析。同时，应结合已有研究成果，进一步研究海底管道作业时可能存在的风险并进行定量的评估和检测，为海洋工程施工安全提供更为坚定的基础。

[ 1 ] LENCI S, CALLEGARI M. Simple Analytical Models for the J-Lay Problem[J].Acta Mechanica, 2005, 178(1-2): 23-29.

[ 2 ] PLUNKETT R. Static Bending Stress in Catenaries and Drill String[J]. Journal of Engineering for Industry, 1967, 89(01): 31-36.

[ 3 ] 胡灵斌，唐军.悬链线方程的求解及其应用[J].船舶，2004，1(01)：17-20.

[ 4 ] 王丹，刘家新.一般状态下悬链线方程的应用[J].船海工程，2007，36(03)：26-28.

[ 5 ] 谢文博，付明玉.铺管船定位作业时的建模与分析[J].中国造船，2011，52(03)：101-108.

[ 6 ] 程闵，段梦兰，李维，等.深水弃置回收作业管线有限元数值分析[J].石油矿场机械，2011，40(10)：41-44.

[ 7 ] BAI Y, BAI Q. Subsea Pipelines and Risers[M]. Amsterdam: Elsevier Science Ltd.， 2005：625-627.

[ 8 ] ZENG X H, LIU C T, XING J Z. Mechanics of Offshore Pipelines in Several Operating States and Analyzing Software[C]//Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering， Oslo, 2002: 73-80.

[ 9 ] 甄国强，胡宗武.铺设过程中海底管道的非线性分析[J].海洋工程，1993，11(03)：28-38.

[10] KIM M H, RAN Z, ZHENG W. Hull/Mooring Coupled Dynamic Analysis of a Truss Spar in Time Domain[J]. International Journal of Offshore and Polar Engineering, 2001, 11(01): 42-54.

[11] 陈海飞.深水柔性立管非线性静动力分析[D].青岛：中国海洋大学，2011: 52-54.

[12] YING M L, ROBIN S L. Dynamic Analysis of a Flexible Hanging Riser in the Time and Frequency Domain[C]//Proceedings of the 25st International Conference on Offshore Mechanics and Arctic Engineering，Hamburg, 2006.

[13] 聂孟喜，王旭升，王晓明，等.风、浪、流联合作用下系统系泊力的时域计算方法[J].清华大学学报(自然科学版)，2004，44(09)：1214-1217.

[14] JENSEN G A. Offshore Pipelaying Dynamics [D]. Norway: NTNU, 2010.

[15] MAREK S. Dynamic Analysis of an Offshore Pipe Laying Operation Using the Reel Method[J]. Acta Mechanica Sinica, 2011, 27(01): 44-55.

[16] LI Z G, CHEN Y, GONG S F, et al. Configuration of Submarine Pipeline for Deepwater S-Lay Technique[C]// Proceedings of the 20th International Offshore and Polar Engineering Conference，Beijing, 2010：188-193.

[17] 马锐.非线性有限元法在海底管道铺设中的应用[D].大连：大连理工大学，2007.

[18] 徐德会.确定海洋管道铺设作业参数的软件实现[D].大连：大连理工大学，2001.

[19] 肖越，王言英.浮体锚泊系统计算分析[J]. 大连理工大学学报，2005，45(05)：682-686.

[20] CHEN X. Studies on Dynamic Interaction Between Deep-Water Floating Structures and Their Mooring/Tendon Systems[D]. Texas: Texas A & M University, 2002：112-114.

[21] RAMAN-NAIR W, BADDOUR R E. Three-Dimensional Dynamics of a Flexible Marine Riser Undergoing Large Elastic Deformations[J]. Multibody System Dynamics, 2003, 10(01): 393-423.

[22] POLLIO A, LANGLEY L R, LOW Y M. A Comparison of Time Domain and Frequency Domain Analysis of a Flexible Marine Riser Undergoing Large Deformations by a Lumped Mass Approach[C]//Proceedings of the 16th International Offshore and Polar Engineering Conference，California, 2006.

[23] 孟丹，郭海燕.深水钢悬链线立管顺流向非线性动力分析[J]. 船舶力学，2012(Z1)：127-135.

[24] 童波，杨建民，李欣. 深水半潜式平台系泊系统动力特性研究[J]. 海洋工程，2009(01):1-7.

[25] GOBAT J I, GROSENBAUGH M A. Application of the Generalized-α Method to the Time Intergration of the Cable Dynamic Equations[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(01): 4817-4829.

[26] GOBAT J I, GROSENBAUGH M A. Time-Domain Numerical Simulation of Ocean Cable Structures[J]. Ocean Engineering, 2006, 33(Z1): 1373-1400.

ReviewofSuspendedSubmarinePipelineModellingandAnalysisTechniques

WANG Wenwei1, ZHANG Mengmeng2a,2b, LIANG Shuting3

(1.Offshore Oil Engineering Co.,Ltd., Tianjin 300461, China; 2. a.State Key Laboratory of Ocean Engineering， b.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiaotong University, Shanghai 200240, China; 3.Tianjin Shiprepairing Technology Research Institute, Tianjin 300456, China)

The common modelling approach of suspended submarine pipeline in the space: catenary method, nonlinear beam theory, elastic rod theory, lumped mass method and rigid finite element method， are introduced, the computational accuracy and efficiency of each method are analyzed, and the scope of application is pointed out. The numerical algorithms of the time used in static and dynamic analysis of pipeline are summarized and their advantages and disadvantages are listed. The research status of suspended submarine pipeline modelling and analysis techniques are summarized, and future research works are discussed.

suspended pipeline; mechanical model; static analysis; dynamic analysis; review

2016-05-10

高技术船舶科研项目“3 000 m水深大型起重铺管船自主研发”(Z12SJENA0011)

王文伟(1989-)，男，硕士研究生

1001-4500(2017)04-0001-06

O327

： A