两种典型覆冰斜拉索气动特性及驰振分析

王凯丽，谭冬梅，瞿伟廉，罗素珍，连世豪，周武辉

（1.武汉理工大学 道路桥梁与结构工程湖北省重点实验室，武汉 430070；2.武汉福星惠誉地产有限公司，武汉 430070）

两种典型覆冰斜拉索气动特性及驰振分析

王凯丽1，谭冬梅1，瞿伟廉1，罗素珍1，连世豪1，周武辉2

（1.武汉理工大学 道路桥梁与结构工程湖北省重点实验室，武汉 430070；2.武汉福星惠誉地产有限公司，武汉 430070）

应用FLUENT中的SSTk-ω模型对不同风速下三维新月形、D形覆冰斜拉索的绕流场进行数值模拟，得到了0°～60°风攻角下的阻力系数、升力系数以及驰振力系数，并与直向拉索的模拟数据进行对比，进而研究风速、覆冰类型、风攻角以及斜向角度对拉索气动特性和驰振稳定性的影响规律。结果表明：风速、覆冰类型、风攻角以及斜向角度对覆冰斜拉索的阻力系数、升力系数均有影响，且影响规律不尽相同；经过计算，在特定风攻角处，覆冰斜拉索的驰振力系数小于0，具有发生覆冰驰振的可能性；通过比较各模拟数据，可以看出直索不能代替斜拉索进行数值模拟来研究其气动特性及驰振稳定性。

振动与波；桥梁工程；覆冰驰振；数值模拟；气动参数；斜拉索

近年来斜拉桥的跨径越来越大，致使斜拉索越来越柔，更容易发生风致振动。在风的作用下，当斜拉索表面呈现干、湿或覆冰三种情况时均会发生振动，尤其是斜拉索偏心覆冰后，截面发生改变，气动外形不再稳定。监测表明覆冰桥梁拉索在-5℃～0℃之间时会出现大振幅的风致振动，严重时可能导致结构失效，因此，有必要对覆冰斜拉索的气动特性和驰振稳定性进行研究。在覆冰驰振研究方面，很多学者对导线驰振进行了较深入的研究，Luongo等采用曲梁单元模拟覆冰导线，分析了覆冰导线的驰振特性[1–2]；马文勇和顾明等对不同覆冰类型导线的气动力特性进行研究[3–4]；楼文娟等对覆冰导线气弹模型舞动进行风洞试验研究，并分析不同覆冰厚度对导线气动特性的影响[5–6]。

由于导线直径远小于斜拉索的直径，并且两者的覆冰情况、热力特性均不同，因此覆冰斜拉索与覆冰导线不能相提并论[7]。Gjelstrup等通过风洞试验对悬索桥覆冰吊杆的气动力和振动稳定性进行分析[8]；Koss等利用结冰风洞研究圆柱积冰的形状特征，为覆冰拉索研究提供了数据[9]；李寿英对覆冰拉索进行理论分析、风洞试验分析以及二维数值模拟研究，并对缠绕螺旋线斜拉索进行数值模拟[10–12]；Demartino等利用风洞试验分析覆冰拉索的气动稳定性[13]。现阶段在桥梁工程领域，虽然国内外学者对覆冰拉索进行了一定的研究，但由于现场实测和风洞试验的局限性，关于覆冰斜拉索的研究资料相对较少。本文利用计算流体力学（CFD）方法对覆冰斜拉索的绕流场进行数值模拟，采用三维模型，考虑实际工程中斜拉索的斜向角度，获得新月形、D形两种覆冰类型斜拉索在不同风速、攻角下的阻力系数、升力系数和驰振力系数，并与直向拉索绕流场的模拟数据进行对比，进而研究覆冰斜向拉索的驰振稳定性，结果表明风速、覆冰类型、风攻角以及斜向角度对覆冰斜拉索的气动特性和驰振稳定性均有影响。

1 横向驰振原理

1.1 气动力参数

覆冰拉索的升力系数和阻力系数采用以下定义式

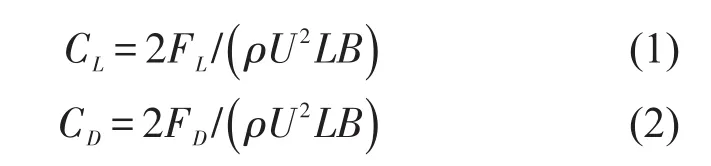
式中CL、CD分别为升力系数和阻力系数；FL为拉索模型的升力，来流速度方向逆时针转动90°为升力的正方向；FD为拉索模型的阻力，沿来流方向为正；ρ为空气密度，取为1.225㎏/m3；U为前方均匀来流风速；B为拉索模型截面特征长度；L为拉索模型长度。

1.2 覆冰拉索横向驰振原理

偏心覆冰拉索在风的激励下，在其上产生升力，并且升力系数随风攻角变化而发生改变，依据Den Hartog驰振理论[14]，当升力系数曲线斜率的负值大于阻力系数时，振动系统的阻尼项为负，系统失稳，此时覆冰拉索可能发生驰振，即驰振发生的描述为

2 模型建立与数值模拟方法

2.1 模型的建立

斜拉索选自某大跨斜拉桥，斜拉索的结构参数见表1，直向拉索的倾角为90°，其它结构参数同斜拉索。斜拉索覆冰选取新月形、D形两种典型冰型，直索覆冰仅选取新月形，覆冰厚度及模型外形尺寸见图1、图2。模拟计算时风攻角以5°递增，风攻角示意图见图3。

表1 斜拉索结构参数

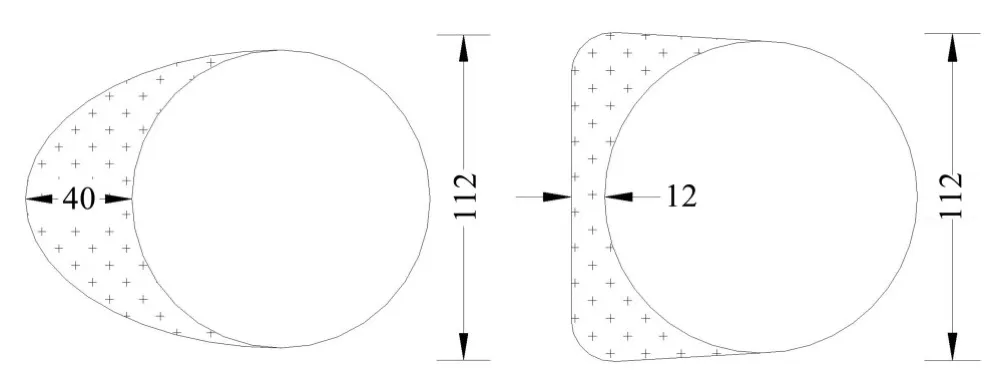
图1 新月形、D形覆冰拉索模型截面图/mm

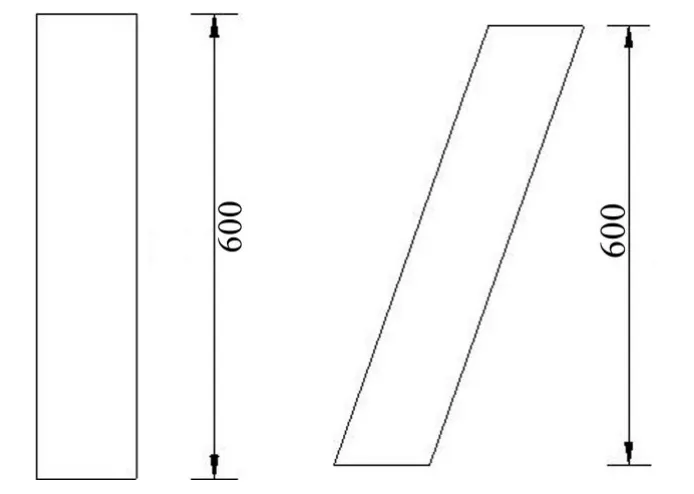
图2 新月形、D形覆冰直向、斜向拉索模型立面图/mm

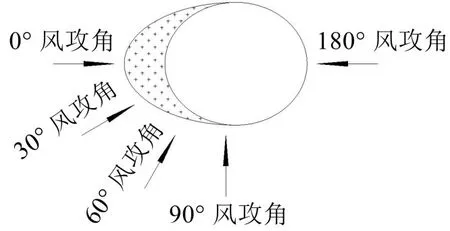
图3 风攻角示意图

覆冰拉索的风攻角变化范围取为0°～60°。由于针对模型每一风攻角工况都进行建模、划分网格比较麻烦且费时，因此对于各风攻角工况保持模型和网格不变，在模拟计算中仅仅改变来流速度方向，计算流域采用正方形区域，区域的大小为4.5 m×4.5 m，拉索放置于整个流域沿流向的1/3位置处，大约距离左边界和下边界为1.5 m，距离上边界和右边界为3.0 m，计算区域尺寸和区域坐标详见图4，图中X轴正方向为0°风攻角方向，水平向右，Y轴正方向为90°风攻角方向，竖直向上，Z轴为流域的厚度方向，以垂直纸面向上为正。

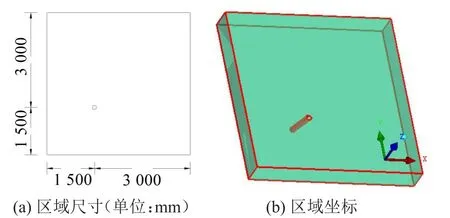
图4 计算区域尺寸及坐标

三维覆冰拉索绕流场采用Ansys ICEM CFD进行网格划分，形成结构化网格，覆冰拉索周围边界层网格采用外O形网格，并对边界层网格进行加密，展向网格沿索划分，网格划分见图5。网格总量约300万，壁面Y+为2。

2.2 数值模拟方法

流域边界条件的定义如下：当风攻角为0°时，图4中流域左边界定义为速度入口，右边界定义为压力出口，Z向上下壁面定义为对称边界，其他定义为固壁边界；当风攻角为5°～60°时，图4中流域左边界和Y向下边界定义为速度入口，右边界和Y向上边界定义为压力出口，Z向上下壁面定义为对称边界，其他定义为固壁边界。文中采用数值模拟方法模拟新月形覆冰直向拉索绕流场，绕流场的进口速度取为12 m/s。同时模拟新月形、D形覆冰斜拉索绕流场，每种覆冰的绕流场进口速度再分别取为12 m/s和16 m/s。

求解器选用基于压力法的求解器，三维空间（3D）采用非稳态计算方法，时间步长取0.001 s。湍流模型采用SSTk-ω模型，松弛因子采用默认，动量、湍动能、比耗散采用2阶迎风格式，采用Simplec算法。

3 覆冰斜拉索数值模拟结果

3.1 60°风攻角下速度流场分布

为了分析风攻角为60°时覆冰斜拉索不同位置处的流场速度分布，取各模型Z=200 mm、Z=400 mm、Y=0三个典型监控截面。图6、图7、图8、图9、图10分别给出了同一时刻风速为V=12 m/s时新月形覆冰直索以及风速为V=12 m/s、V=16 m/s、覆冰类型为新月形、D形的斜拉索在风攻角为60°时相应监控截面的速度云图，从图中可以看出覆冰拉索尾流中存在旋涡的形成和脱落，拉索迎风两侧形成的尾流旋涡区域速度较大，背风面形成的旋涡区域速度很小。图6中监控截面的尾流脱落旋涡大小、颜色、散发形式基本相同，而图7、图8、图9、图10中Z=200 mm和Z=400 mm监控截面的脱落旋涡大小、颜色均不相同，说明速度值不一样，并且脱落散发形式也有着明显的差别，说明覆冰直索不能代替覆冰斜拉索进行绕流场数值模拟。

图5 覆冰拉索网格划分

图6 V=12 m/s时新月形覆冰直索监控截面的速度分布/(m∙s-1)

图7 V=12 m/s时新月形覆冰斜拉索监控截面的速度分布/(m∙s-1)

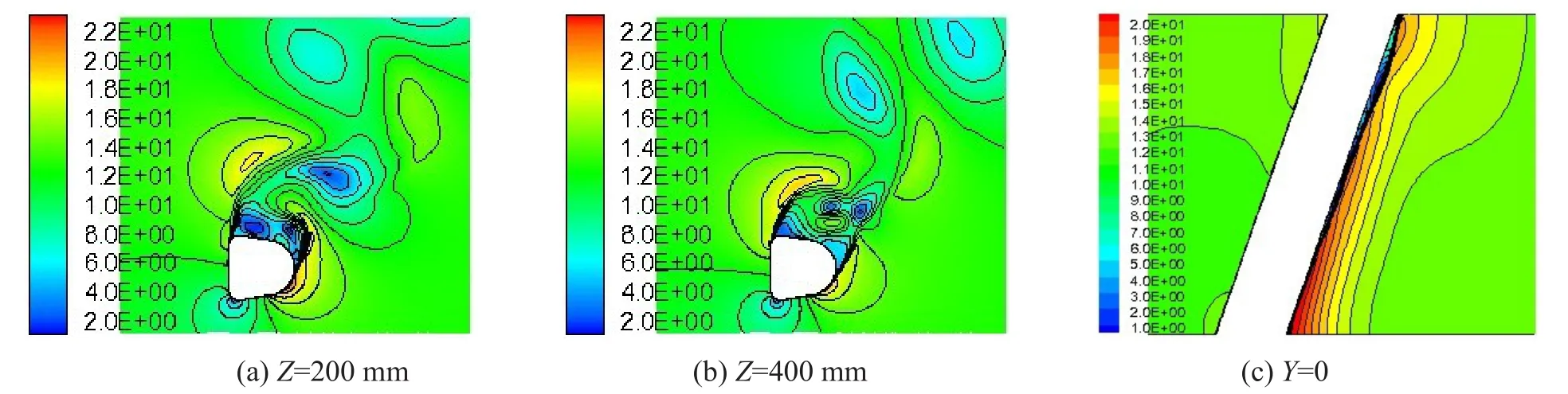
图8 V=12 m/s时D形覆冰斜拉索监控截面的速度分布/(m∙s-1)

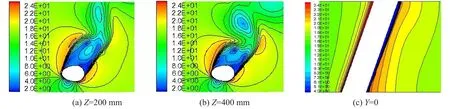
图9 V=16 m/s时新月形覆冰斜拉索监控截面的速度分布/(m∙s-1)

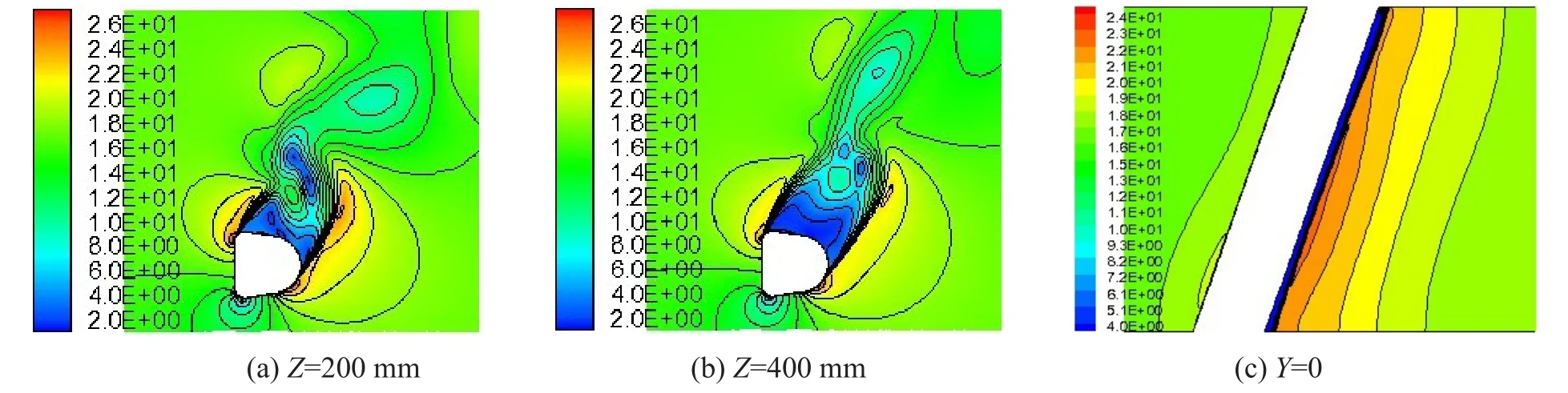
图10 V=16 m/s时D形覆冰斜拉索监控截面的速度分布/(m∙s-1)

3.2 0°～60°风攻角下覆冰斜拉索的气动力系数

通过数值风洞模拟分别得到12 m/s风速下新月形覆冰直索以及12 m/s、16 m/s风速下新月形、D形覆冰斜拉索在0°～60°风攻角下的阻力系数和升力系数时程曲线，进而获得时程稳定后覆冰拉索的阻力系数和升力系数的平均值，其平均值随风攻角的变化规律如图11、图12所示。

图11分别给出了12 m/s风速下新月形覆冰直索以及12 m/s、16 m/s风速下新月形、D形覆冰斜拉索在0°～60°风攻角下的平均阻力系数。图中新月形覆冰拉索的阻力系数均随风攻角先略有下降再平稳上升，在60°时达到最大值，分别为1.35、1.0、0.8，在风攻角0°～60°范围内，除30°风攻角外，12 m/s风速下的新月形覆冰斜拉索的阻力系数均大于16 m/s风速下的新月形覆冰斜拉索的阻力系数，并且在风攻角30°～60°范围内，随风攻角增大，两者的差值越来越大。对于D形覆冰斜拉索，12 m/s、16 m/s风速下的阻力系数随风攻角的波动趋势一致，先大幅下降，再呈阶梯状上升，12 m/s风速下的阻力系数下降幅度小于16 m/s风速下的值，风攻角在15°～60°范围内形成两个峰，12 m/s风速下的阻力系数波动比较大，上升较快，而16 m/s风速下的阻力系数在风攻角为20°～60°范围内波动平缓，上升较慢。在风攻角为0°～60°范围内，与新月形覆冰拉索相似，12 m/s风速下的D形覆冰斜拉索的阻力系数均大于16 m/s风速下的D形覆冰斜拉索的阻力系数，说明风速变大，阻力系数减小，但不同风速下阻力系数随风攻角的变化趋势并未改变。

图11 覆冰斜拉索阻力系数

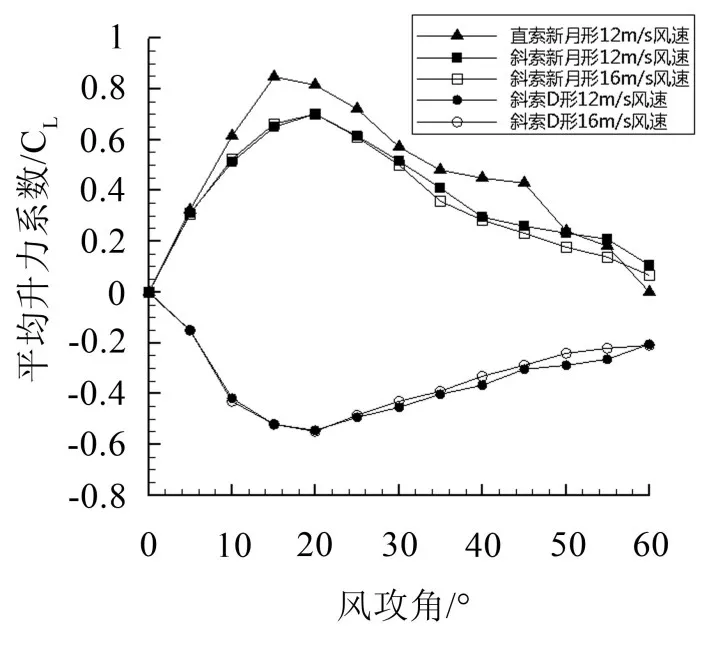
图12 覆冰斜拉索升力系数

图12分别给出了12 m/s风速下新月形覆冰直索以及12 m/s、16 m/s风速下新月形、D形覆冰斜拉索在0°～60°风攻角下的平均升力系数。

图中同一覆冰类型在不同风速下的覆冰拉索的升力系数随风攻角变化趋势一致，对于新月形覆冰直向、斜向拉索，升力系数随风攻角变化曲线均呈现倒“V”状，而对于D形覆冰斜拉索，升力系数随风攻角变化曲线呈现正“V”状，在20°风攻角处达到最小值，约为-0.55。在风攻角为0°～25°范围内，同一覆冰类型在不同风速下的覆冰斜拉索的升力系数值比较接近，在风攻角为30°～55°范围内，相应的升力系数差值随风攻角增大逐渐增大，在60°风攻角处有差值变小的趋势，并且在风攻角为25°～60°范围内，16 m/s风速下覆冰斜拉索的升力系数绝对值均小于12 m/s风速下覆冰斜拉索的升力系数绝对值。

从图11、图12中看出风攻角的变化会引起覆冰斜拉索周围绕流场的变化，从而造成覆冰斜拉索的气动力系数随风攻角发生改变，而气动力系数随风攻角发生改变是导致覆冰斜拉索发生驰振的重要原因。对图中直索的气动力系数与相应条件下的斜拉索气动力系数进行比较，可以看出两者数据相差较大，因此数值模拟中不能把斜拉索简化为直索进行模拟获得数据。以上结论综合表明风速、覆冰类型、风攻角以及斜向角度对覆冰斜拉索的阻力系数、升力系数均有影响，其中风速对阻力系数的影响较大，对升力系数的影响不太明显，斜向角度对二者数值均有较大影响，但是风速的变化、斜向角度并未改变气动力系数随风攻角的变化趋势，而覆冰类型、风攻角对阻力系数、升力系数数值和随风攻角的变化趋势均有较大影响。

3.3 0°～60°风攻角下覆冰斜拉索驰振力系数

为了判断覆冰斜拉索发生驰振的可能性，运用式（3）计算可得到平均升力系数随风攻角变化曲线的斜率值与相应平均阻力系数的矢量和，即驰振力系数，但对于一个特定风攻角而言，升力系数曲线的斜率值可能取决于左侧曲线斜率或者右侧曲线斜率[15]。文中将两种情况下不同风速时、不同覆冰类型的直向、斜向拉索随风攻角变化的左、右驰振力系数分别列于图13、图14中，当某风攻角处升力系数左侧曲线斜率和右侧曲线斜率分别对应的驰振力系数同时小于0时，才认为覆冰拉索处于不稳定状态。从图13中看出新月形覆冰斜拉索在不同风速下的左驰振力系数随风攻角的波动趋势比较一致，先下降再上升，在风攻角为0°～30°范围内，左驰振力系数相差很小。对于D形覆冰斜拉索，在风攻角为0°～30°范围内，左驰振力系数也相差很小，但在风攻角为35°～60°范围内，12 m/s风速下的左驰振力系数与16 m/s风速下的左驰振力系数波动趋势刚好相反。图14为覆冰斜拉索的右驰振力系数，波动趋势与左驰振力系数曲线相似。

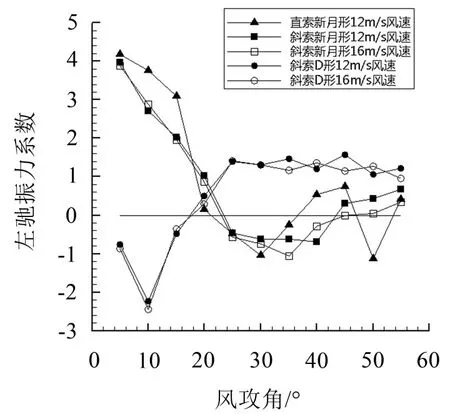
图13 覆冰斜拉索左侧曲线斜率对应的驰振力系数

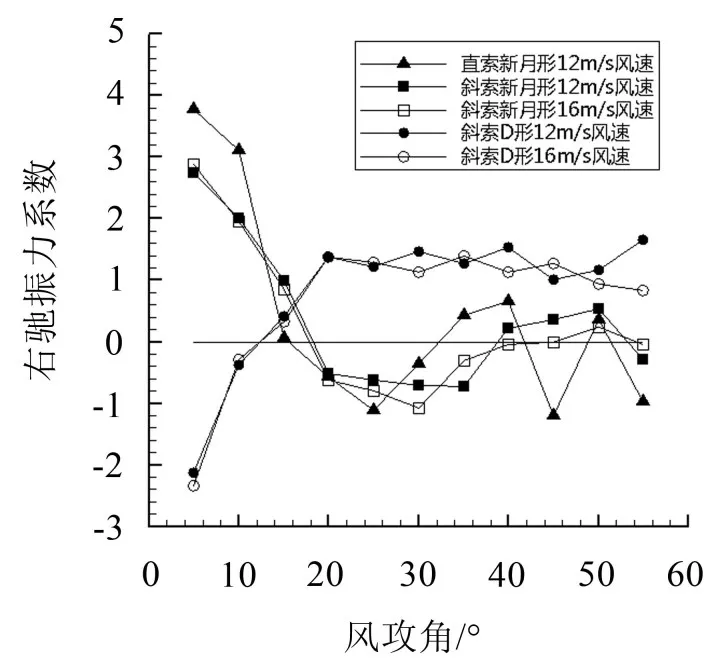
图14 覆冰斜拉索右侧曲线斜率对应的驰振力系数

相对于新月形覆冰斜拉索，新月形覆冰直索的驰振力系数波动剧烈，两者数值相差较大，更加说明直索不能代替斜拉索进行数值模拟。在风攻角在0°～60°范围内，对于不同条件下的左、右驰振力系数，均存在小于0的情况，说明覆冰斜拉索具有发生驰振的可能性。

经过整理，覆冰直向、斜向拉索可能发生驰振的风攻角汇总见表2，从表中可以看出，在25°、30°风攻角处，12 m/s风速下新月形覆冰直索左侧曲线斜率和右侧曲线斜率分别对应的驰振力系数均为负值；在25°、30°、35°风攻角处，12 m/s风速下新月形覆冰斜拉索左侧曲线斜率和右侧曲线斜率分别对应的驰振力系数均为负值；在25°、30°、35°、40°、45°风攻角处，16 m/s风速下新月形覆冰斜拉索的左、右驰振力系数均为负值；在5°、10°风攻角处，12 m/s、16 m/s风速下D形覆冰斜拉索的左、右驰振力系数均为负值，都满足Den Hartog驰振发生的条件，容易发生覆冰驰振。

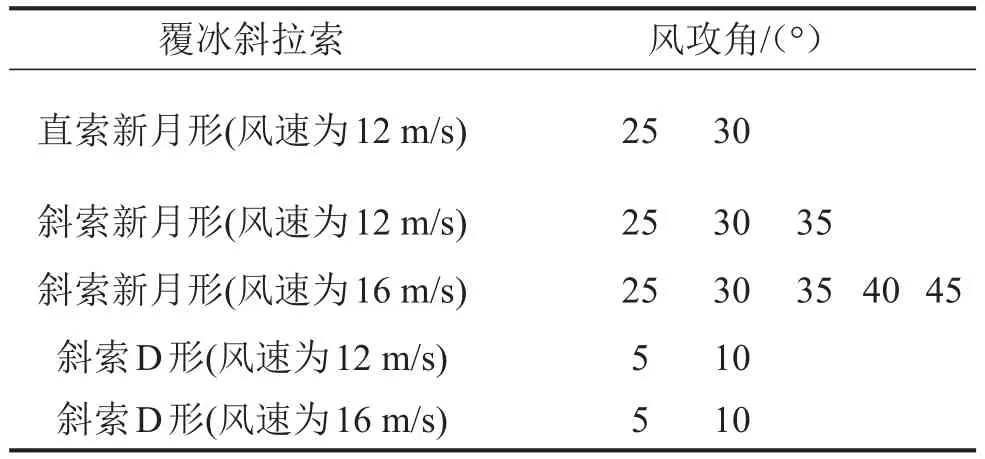
表2 斜拉索易发生覆冰驰振的风攻角

以上结果表明，对于新月形覆冰斜拉索，虽然负驰振力系数对应的风攻角范围大，但其绝对值比较小，发生驰振需要的临界风速比较大，而D形覆冰斜拉索的负驰振力系数对应的风攻角范围虽然比较小，但其绝对值比较大，发生驰振需要的临界风速相对较小，即D形覆冰斜拉索可能比新月形覆冰斜拉索更危险。

4 结语

利用FLUENT软件对新月形覆冰直索以及不同风速下三维新月形、D形覆冰斜拉索模型的绕流场进行数值模拟，得到覆冰拉索在0°～60°风攻角下的气动力系数和驰振力系数并进行比较，进而分析覆冰斜拉索的气动特性和驰振稳定性，得到如下结论：

(1)相对于直索，同一时刻、同一风速下、同一覆冰类型的斜拉索不同监控截面的尾流旋涡脱落散发形式有着明显的差别，说明覆冰直索不能代替覆冰斜拉索进行绕流场数值模拟。

(2)风速、覆冰类型、风攻角以及斜向角度对覆冰斜拉索的阻力系数、升力系数均有影响，其中风速对阻力系数的影响较大，对升力系数的影响不太明显，斜向角度对二者数值均有较大影响，但是风速的变化、斜向角度并未改变气动力系数随风攻角的变化趋势，而覆冰类型、风攻角对阻力系数、升力系数数值和随风攻角的变化趋势均有较大影响。

(3)在风攻角为0°～60°范围内，不同风速、不同覆冰类型的斜拉索左、右驰振力系数均存在同时小于0的情况，说明覆冰斜拉索具有发生覆冰驰振的可能性，并且通过比较各模拟数据，可以看出直索不能代替斜拉索进行数值模拟来研究其气动特性及驰振稳定性。

(4)对于新月形覆冰斜拉索，虽然负驰振力系数的风攻角范围大，但其绝对值比较小，发生驰振需要的临界风速比较大，而D形覆冰斜拉索的负驰振力系数的风攻角范围虽然比较小，但其绝对值比较大，发生驰振需要的临界风速相对较小，即D形覆冰斜拉索可能比新月形覆冰斜拉索更危险。

[1]LUONGO A,ZULLI D,PICCARDO G.A linear curvedbeam model for the analysis of galloping in suspended cables[J].Journal of Mechanics of Materials and Structures,2007,2(4):675-694.

[2]LUONGO A,ZULLI D,PICCARDO G.Analytical and numerical approaches to nonlinear galloping of internally resonant suspended cables[J].Journal of Sound and Vibration,2008,315:375-393.

[3]马文勇，顾明.扇形覆冰导线气动力特性及驰振不稳定性研究[J].振动与冲击，2012，31(11)：82-85.

[4]马文勇，顾明，全涌，等.准椭圆形覆冰导线气动力特性试验研究[J].同济大学学报(自然科学版)，2010，38(10)：1409-1413.

[5]楼文娟，王昕，许福友.覆冰导线气弹模型舞动风洞试验研究[J].土木工程学报，2011，44(11)：18-23.

[6]楼文娟，林巍，黄铭枫，等.不同厚度新月形覆冰对导线气动力特性的影响[J].空气动力学学报，2013，31(5)：616-622.

[7]DEMARTINO C,KOSS H H,GEORGAKIS C T,et al.Effects of ice accretion on the aerodynamics of bridge cables[J].Journal of Wind Engineering and Industrial Aerodynamics,2015,138:98-119.

[8]GJELSTRUP H,GEORGAKIS C T,LARSEN C T.An evaluation of iced bridge hanger vibrations through wind tunnel testing and quasi-stedy theory[J].Wind and Structures,2012,15(5):385-407.

[9]KOSS H H,GJELSTRUP H,GEORGAKIS C T.Experimental study of ice accretion on circular cylinders atmoderatelow temperatures[J].Journalof Wind Engineering and Industrial Aerodynamics,2012,S104-106(3):540-546.

[10]李寿英，黄韬，叶继红.覆冰斜拉索驰振稳定性的理论研究[J].振动与冲击，2013，32(1)：122-127.

[11]李寿英，黄韬，叶继红.覆冰斜拉索气动力的试验与数值研究[J].湖南大学学报，2012，39(8)：1-6.

[12]李寿英，钟卫，陈政清.缠绕螺旋线斜拉索气动性能的数值模拟[J].振动工程学报，2014，27(4)：488-496.

[13]DEMARTINO C,RICCIARDELLI F.Aerodynamic stabili-ty of ice-accreted bridge cables[J].Journal of Fluids and Structures,2015,52:81-100.

[14]DEN HARTOG J P.Transmission line vibration due to sleet[J].Transactions of the American Institute of Electrical Engineers,1932,51(4):1074-1077.

[15]CHENG SHAOHONG,IRWIN PETER A,TANAKA HIROSHI.Experimental study on the wind-induced vibration ofa dry inclined cable-partⅡ:proposed mechanisms[J].Journal of Wind Engineering and IndustrialAerodynamics,2008,96(12):2254-2272.

Analysis ofAerodynamic Characteristics and Galloping Performance for Two Typical Iced Stay Cables

WANG Kai-li1,TAN Dong-mei1,QU Wei-lian1,LUO Su-zhen1,LIAN Shi-hao1,ZHOU Wu-hui2
（1.Hubei Key Lab of Roadway Bridge&Structure Engineering,Wuhan University of Technology,Wuhan 430070,China;2.Wuhan Fuxing Huiyu Real Estate Co.Ltd.,Wuhan 430070,China)

The flow fields of 3D crescent-shaped and D-shaped iced stay cables under different wind speeds are simulated respectively applying SST k-ω model of FLUENT code.The drag and lift coefficients and galloping coefficients of the iced stay cables with 0°～60°wind attack angles are computed and compared with the simulation data of the straight cables.The influences of wind speed,icing type,wind attack angles and oblique angles on the aerodynamic characteristics and galloping stability of the stay cables are studied.The results show that the wind speed,the icing type,the wind attack angles and the oblique angles have some influences on the drag and lift coefficients,but the influence rules are different.Galloping coefficients of the iced stay cables with some particular wind attack angles are negative.So,these stay cables have the possibility of galloping vibration.Through mutual comparison of the simulation data,it is found that the stay cables cannot be represented by the straight cables in numerical simulation analysis of the aerodynamic characteristics and galloping stability.

vibration and wave;bridge engineering;icing galloping;numerical simulation;aerodynamic parameters;stay cables

U441+.3

：A

：10.3969/j.issn.1006-1355.2017.04.025

1006-1355(2017)04-0126-06+137

2016-12-26

国家自然科学基金资助项目（51408452）；湖北省重点实验室开放基金资助项目（DQJJ201509）

王凯丽（1991－），女，河南省周口市人，硕士生，主要研究方向为结构健康监测与损伤诊断。

谭冬梅，女，硕士生导师。

E-mail:smiledongmei@163.com