航向角偏差对飞行器目标脱靶量精度分析*

曹淑艳

(中国人民解放军92941部队，辽宁 葫芦岛 125000)

航向角偏差对飞行器目标脱靶量精度分析*

曹淑艳

(中国人民解放军92941部队，辽宁 葫芦岛 125000)

从脱靶量处理中所用到重要参数航向角进行分析，推导了船体中心点坐标计算方法，评估航向角测量误差在位置转换中对脱靶量的影响。同时也针对被跟踪目标的靶载GPS测量设备的布设点的位置变化，分析对脱靶量处理结果的影响程度。通过大量仿真模拟数据及实测数据的检验，验证了提出的方法准确合理，可在外测数据处理中广泛应用。

航向角；脱靶量；船体中心；GPS测量设备；船体坐标系；大地坐标

0 引言

航向角是目标在水平面内的速度分量与真北的夹角，它在飞行器目标脱靶量的计算中是一个很重要的参数，航向角偏差直接影响飞行器脱靶量的精度[1-4]。实际应用中考核飞行器目标的脱靶量，是以偏离靶标中心的纵向及侧向偏差来表征的[5-7]。模拟靶目标的船体中心即是它的散射中心，在试验中，由于被攻击目标的电磁环境复杂，GPS(global positioning system)无法装载在船体中心点上，GPS测量点一般是选择安装在舰艏、舰尾或远离复杂电磁环境的位置。因此，须将GPS测量点数据转到船体中心点并作为该点的数据，在此坐标修正中，对航向角的测量值要求较高。本文正是基于这样的工程背景，来分析航向角偏差对飞行器目标脱靶量精度的影响[8-9]。

1 船体坐标系建立[10-12]

假设跟踪的攻击目标为靶船，建立船体坐标系时，原点O为飞行器过船体中心所在水平面时刻的靶体中心点，Ox轴：过坐标原点的切平面内，指向船艏方向；Oy轴：过坐标原点的切平面的法线，指向向上；Oz轴：过坐标原点的切平面内，与Ox，Oy轴构成右手直角坐标系。GPS与船体中心位置关系图如图1所示。

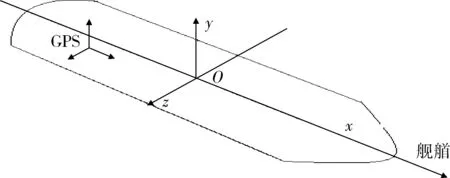
图1 GPS与船体中心位置关系图Fig. 1 Relationship between GPS and hull center position

2 船体中心点坐标计算方法

已知GPS测量点数据，求船体中心点数据。设GPS测站的地心坐标(WGS-84坐标系)为(xGPS，yGPS，zGPS)，大地坐标(WGS-84坐标系)为(BGPS，LGPS)，GPS测量点在船体坐标系下的三维坐标为(xTO，yTO，zTO)。当需要将GPS设备测点修正到船体中心点时，采用参系修正法。它们之间的位置关系如图2，3所示。

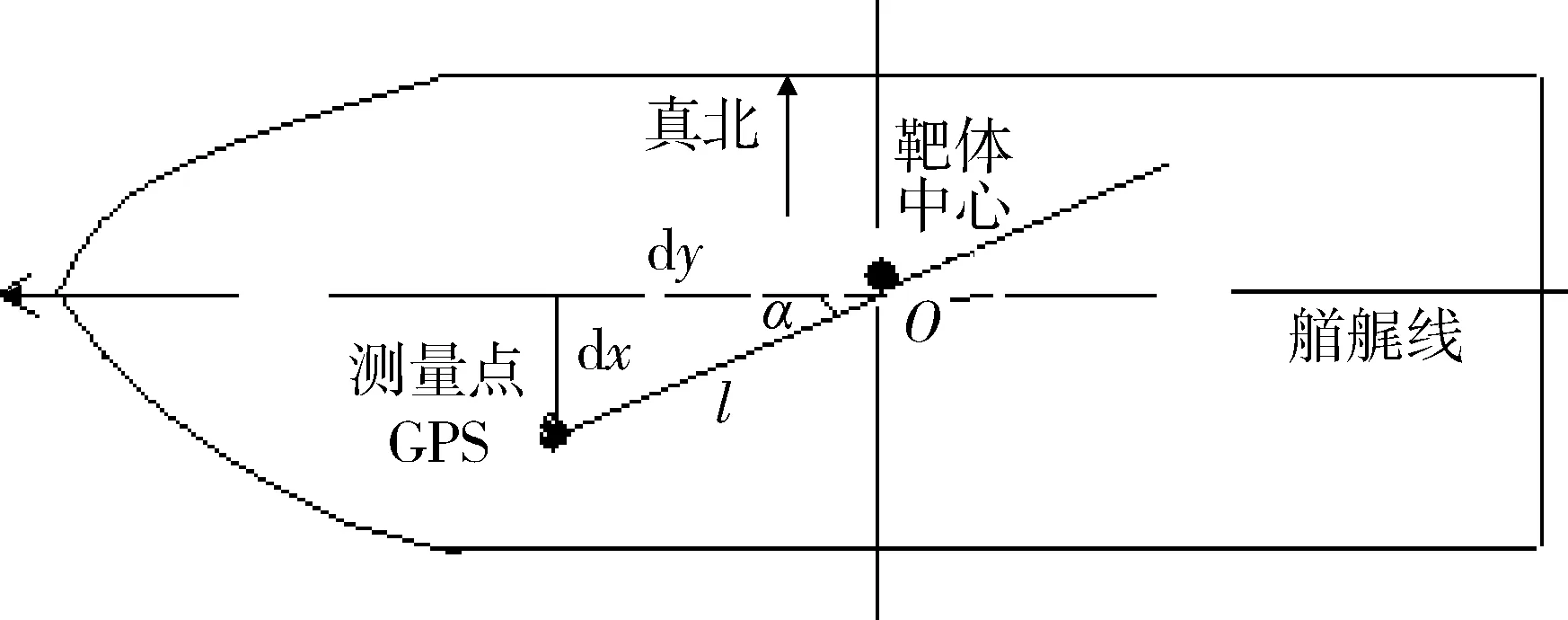
图2 GPS测量设备与船体中心转换关系水平面图Fig. 2 Horizontal view of transfer relation between GPS device and hull center

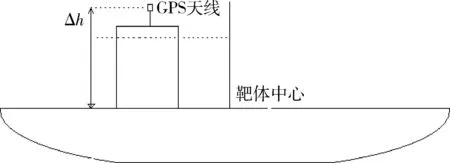
图3 GPS测量设备与船体中心转换关系纵剖面图Fig. 3 Longitudinal section of transition relationship between GPS device and hull center

此时，船体中心在参考坐标系中的坐标计算公式为

(1)

(2)

(3)

式中:dx，dy，dz为攻击目标中心点在参考系中的坐标。

(4)

式中：α为GPS与船体中心连线与船艏艉线夹角；dx，dy，dz实际上等于实测的GPS到船体中心的三维值；l为GPS测量点与船体间距离。β=Kc-α，β为GPS与船体中心连线与真北间的夹角，Kc船体艏艉线与真北夹角，即航向角。于是，船体中心在WGS-84坐标系下的地心坐标为

(5)

靶体中心点的大地坐标(纬度B，经度L，大地高H)为如下计算模型：

(6)

(7)

(8)

(9)

(10)

式中： e为参考椭球第一偏心率；N为卯酉圈曲率半径；H为大地高；a，b分别为参考椭球的长半径和短半径。

通过上述转换模型计算，再利用脱靶量计算公式，所求得的脱靶量就相当于飞行器目标过靶时相对于靶体中心的脱靶量。

3 航向角偏差给靶船航迹计算结果带来的影响分析

试验前，虽然测量工具及人为因素的影响，Δx，Δy，Δh的测量存在一定的误差，但只要方法正确，误差能控制在亚米级以内。在试验中，被跟踪的目标正常条件下，模型转换误差可以达到忽略不计。因此，航向角Kc的测量是测量点变换修正的关键。航向角的值一方面由靶上的GPS测得的瞬时速度计算得到[13]，另一方面也可由航向角测量设备测量。对于低速运动目标，由于受到水流速度等因素的影响，其艏艉线方向与目标行驶方向并不一致，存在较大误差，那么通过以下算例评估航向角偏差给靶船航迹带来的误差(表1～5内的数据量纲均为米)。

将GPS测量点依次安装在船上不同点，通过第2节的转换模型，分别求出靶体中心点位的航迹数据，与GPS测量点的数据做一次差即为表1～5中的Δx，Δy，Δz，数据结果如表1～5所示。表中分别列出了航向角在精确测量值下的一次差值，相差1°，2°，5°，10°时的一次差值。

通过大量数据分析，并从表1～4列出的表格数据中得到，当靶标测量设备安装在船体附近(10 m左右)时，航向角测量误差在相差1°或2°时，坐标值在0.5 m以内，满足精度指标要求。相差5°或10°，坐标值在2～3 m之间。如果目标测量设备安装在船体尾部距离船体中心较远时，转换结果误差相当大，如表5所示，在航向角相差1°或2°时，转换误差在1.3～2.6 m，而当相差5°或10°，坐标值6.4～12.4 m，严重影响脱靶量计算结果。

表1 GPS安装在靶体中心附近时的修正结果一次差

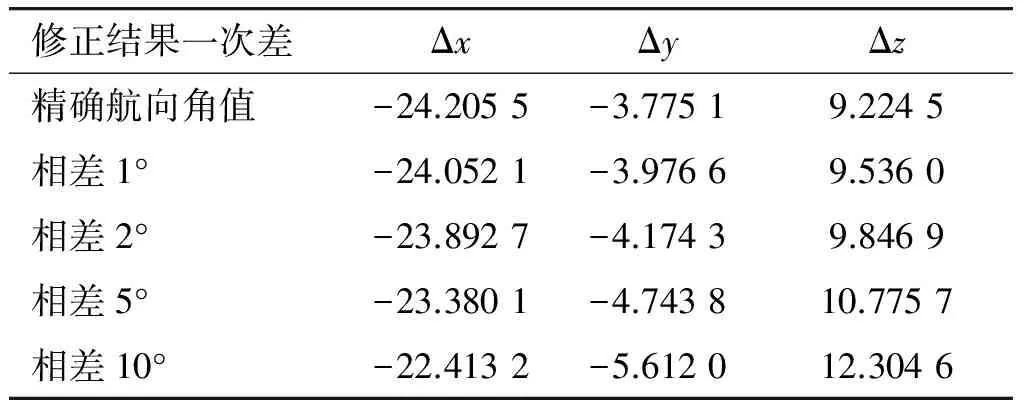
表2 GPS测量点安装在靶体23 m处的修正结果一次差

表3 GPS测量点安装在靶体-23 m处的修正结果一次差

表4 GPS测量点安装在靶体 -16 m处的修正结果一次差

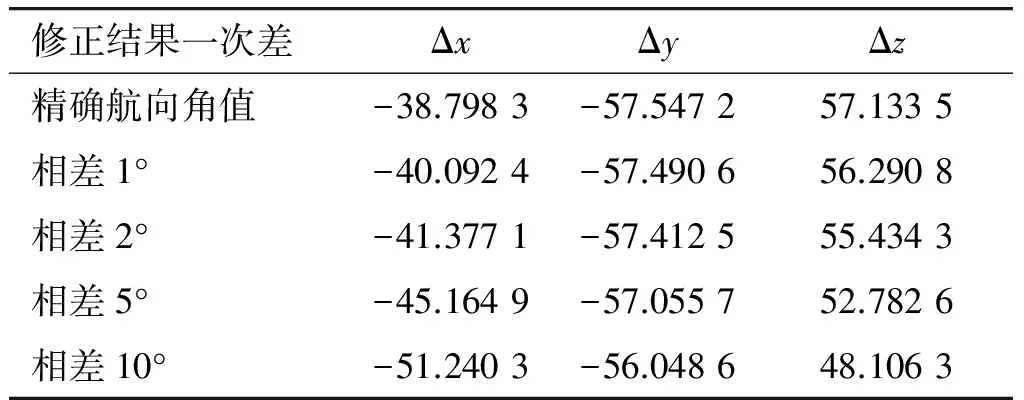
表5 GPS安装在靶88 m处的修正结果一次差

为了验证航向角偏差给考核目标脱靶量带来的误差大小，分别计算GPS测量点在不同位置时，航向角变化后的脱靶量值，并与真值进行比对，从而定量分析航向角偏差对脱靶量精度影响。

从表6，7中数据分析可得出，航向角偏差给脱靶量计算结果带来的误差，是随着航向角偏差的增大，位置转换误差也变大，导致脱靶量精度受到影响，从0.5 m到4.1 m的误差。由于船载航向角测量设备存在误差，航向角相差1°或2°时，存在估算的脱靶量与真值更为接近的情况。为了更好地完成试验，靶体上应安装准确的航向角测量设备，验前也要估算一下安装点架设的最优位置。

表6 GPS安装在靶体附近时的脱靶量处理结果

表7 GPS安装在距靶心11 m处时的脱靶量处理结果

4 结束语

本文从脱靶量处理中所用到重要参数航向角出发，推导靶体中心点坐标计算方法，通过大量仿真模拟数据及实测数据，评估航向角测量误差在位置转换中对脱靶量的影响。同时也针对被跟踪目标的GPS测量设备的布设点的位置变化，对脱靶量结果的影响进行了分析，从数据得出离靶体中心越远，误差越大[14-15]。

由于靶船是慢速目标，通过速度求出的航向角误差比较大，5～十几度范围，在求脱靶量时会超差。因此，试验中需要准确的航向角测量设备，误差在≤1.0°范围内。同时GPS测量点要安装在船体中心10 m以内附近，这样位置转换误差可控制在1 m以内。

本文所论证的方法，准确合理，可在外测数据处理中广泛应用。

[1] 罗海银. 导弹航天测控通信技术词典[M].北京：国防工业出版社，2001: 450-451. LUO Hai- yin. Technical Dictionary of TTC&C for Missile and Space[M]. Beijing: National Defense Industry Press，2001: 450-451.

[2] 周立峰，姜大治，韩先平.高精度发射方位角计算方法研究[J].战术导弹技术，2008(6):13-16. ZHOU Li- feng，JIANG Da- zhi，HAN Xian- ping. Research on the Calculation Method of High Accuracy Azimuth[J].Tactical Missile Technology，2008(6):13-16.

[3] 邬熙娟，江国焰，高俊强. 子午线收敛角计算公式及计算精度分析[J]. 现代测绘，2005，28(6):22-25. WU Xi- juan，JIANG Guo- yan，GAO Jun- qiang. Calculation of Formula of Meridian Constringent Angle and Its Accuracy Analysis[J]. Modern Mapping，2005，28(6):22-25.

[4] 刘利生，张玉祥. 外弹道测量数据处理[M]. 北京：国防工业出版社，2002. LIU li- sheng，ZHANG Yu- xiang. Data Processing of Exterior Ballistic Measurement[M]. Beijing: National Defense Industry Press，2002.

[5] 魏国华，吴嗣亮，王菊，等. 脱靶量测量技术综述[J]. 系统工程与电子技术，2004，26(6)：768-772，847. WEI Guo- hua，WU Si- liang，WANG Ju，et al. Instruction of Miss Distance Measurement Technology[J].Systems Engineering and Electronic Technology，2004，26(6)：768-772，847.

[6] 王永杰. 利用引信多普勒频率估计导弹脱靶量方法研究[J]. 系统工程与电子技术，2005，27(11)：1914-1916． WANG Yong- jie. Estimation of Missile Miss Distance by Using Doppler Frequency of Fuze[J].Systems Engineering and Electronic Technology，2005，27(11)：1914-1916．

[7] 裴赭，史震. 一种估计舰空导弹脱靶量的方法[J]. 海军航空工程学院学报，2010，25(3)：259-262． PEI Zhe，SHI Zhen. A Method of Estimating Missile Miss Distance[J]. Journal of Naval Aeronautical Engineering Institute，2010，25(3)：259-262．

[8] 韩路杰，崔少辉. 利用导引头信息测量脱靶量的方法研究[J]. 系统工程与电子技术，2014，36(4)：734-738． HAN Lu- jie，CUI Shao- hui.Method of Measuring Miss Distance Using Seeker Information[J].Systems Engineering and Electronic Technology，2014，36(4)：734-738．

[9] 房秉毅，王剑. 基于距离跟踪的矢量脱靶量测量方法[J]．弹道学报，2007，19(2)：29-32，50. FANG Bing- yi，WANG Jian. Vector Miss Distance Measurement Based on Range- only Tracking[J]． Journal of Ballistics，2007，19(2)：29-32，50.

[10] 朱华统. 常用大地坐标系及其变换[M]. 北京：解放军出版社，1990． ZHU Hua- tong. Common Geodetic Coordinate Systems and Their Transformations[M]. Beijing: PLA Publishing House，1990.

[11] 鲁郁.GPS全球定位接收机—原理与软件实现[M].北京：电子工业出版社，2009: 11-17. LU Yu. GPS Global Position Receiver: Principle and Software Implement[M]. Beijing :Publishing House of Electronics Industry，2009: 11-17.

[12] 朱华统，郑育富. 大地测量[M]. 北京：测绘出版社，1987:414-421. ZHU Hua- tong，ZHENG Yu- fu. Geodetic Surveying[M]. Beijing: Surveying and Mapping Press，1987:414-421.

[13] 高冰，段一萍. 外弹道数据处理中航向角精确计算方法[J]. 飞行器测控学报，2003(3):26-29. GAO Bing，DUAN Yi- ping. Accurate Calculation of Heading Angle in Exterior Ballistic Data Processing[J]. Aircraft Measurement and Control Journal，2003(3):26-29.

[14] WANG，WU S L． New Method for Extraction of Doppler Frequency in ScaIar Miss Distance Measurement System[J]．Proceedings of SPIE，2005，5637：249-256．

[15] 王辉，吕瑛洁，林德福，等. 扩展弹道成型制导系统脱靶量特性分析[J]. 红外与激光工程，2013，42(5)：1322-1329. WANG Hui，LÜ Ying- jie，LIN De- fu，et al. Analysis of Miss Distance Characteristics of Extended Ballistic Forming Guidance System[J].Infrared and Laser Engineering，2013，42(5)：1322-1329.

Analysis of Course- Angle Deviation on the Precision of Miss Distance of an Aero Craft

CAO Shu- yan

(PLA，No. 92941 Troop，Liaoning Huludao 125000，China)

Based on analyses of the important parameters used in the calculation of miss distance, a method is deduced to calculate the coordinates of the center of a vessel and to estimate the influence of course- angle deviation on the miss distance in position shifting. The influence of the variation of the position of the on- board GPS(global positioning system) equipment in the traced target is also analyzed. Simulations and test data verified the correctness of the proposed method and it can be widely used in trajectory measuring.

course angle; miss distance; vessel centre; GPS(global positioning system) equipments; hull coordinate system; geodetic coordinates

2017-05-08；

2017-06-19 作者简介：曹淑艳(1968-)，女，黑龙江密山人。高工，硕士，主要研究方向为无线电外测数据处理、武器系统。

10.3969/j.issn.1009- 086x.2017.04.019

TJ760.6+2；P228.4

A

1009- 086X(2017)- 04- 0119- 05

通信地址：125000 辽宁葫芦岛市92941部队96分队 E- mail：caoshuyan_ch@163.com