光纤陀螺一维惯性角度测量误差标定技术研究*

杨梦放，陈磊，田慧，张登伟，舒晓武，车双良

(浙江大学a.光电科学与工程学院 现代光学仪器国家重点实验室；b.医学院附属妇产科医院，浙江 杭州 310027)

光纤陀螺一维惯性角度测量误差标定技术研究*

杨梦放a，陈磊a，田慧b，张登伟a，舒晓武a，车双良a

(浙江大学a.光电科学与工程学院 现代光学仪器国家重点实验室；b.医学院附属妇产科医院，浙江 杭州 310027)

针对光纤陀螺的一维惯性角度测量系统长期工作时产生较大的随时间累积误差，提出了一种新型角度测量误差的实时标定方法。此方法基于光学三角法测距的原理，利用2个激光位移传感器测量的位移实现角度的实时测量，在高精度转台上对测试系统进行了实验验证，通过最小二乘拟合法对误差进行了补偿。实验结果表明，该系统的角度测量范围±10°，角度测量精度±0.005°，为光纤陀螺在长时间角度测量方面提供了角度基准。该标定技术使用非接触光学测量方法，对被测物体表面无损伤。

光纤陀螺；误差标定；激光三角法；角度测量；非接触测量；实时

0 引言

基于光纤陀螺和加速度计的新型惯性测量技术能实现对载体运动信息的自主测量，具有高精度、全固态等优点，广泛应用于航空航天飞行器、导弹、舰船与车辆的导航及姿态控制。惯性测量组合的实际应用环境存在振动、温度、磁场等因素，影响实际的导航及姿态测量精度。在地面试验阶段对惯性测量组合进行导航及姿态测量精度的标定，对于惯性测量组合的实际应用具有重要意义。实际的惯性测量组合包含3个正交陀螺和3个正交加速度计，陀螺的测角精度是决定惯性测量组合性能的关键因素之一，研究单个陀螺在振动或转动等动态条件下的角度测量精度，对于惯性测量组合的导航及姿态控制性能意义重大[1-5]。

本文提出了一种基于激光三角法测距原理的非接触一维角度测量技术，利用2个激光位移传感器实时测量与光纤陀螺固联的载体运动位移，计算得到载体转动的实时角度，通过同步采集系统实时同步获取光纤陀螺的角度测量信息，并与计算得到的激光位移传感器角度测量信息进行比较，得到2种测量方法的误差信息，实现对光纤陀螺在动态条件下实时测量误差的标定。该标定技术测试方法简单，使用方便，无需手动对准，对被测物体表面没有损伤，对惯性测量组合导航性能的实时评估具有重要意义。

1 测量系统设计

1.1 激光三角测量位移的原理

如图1所示，光源发出的光经过会聚透镜聚焦后垂直入射到被测物体表面M上，物体移动或表面变化，导致光敏元件CCD(charge- coupled device)上的成像光点移动，对CCD输出的电信号进行运算处理得到传感器与被测物体表面之间的距离信息[6-7]。在接受透镜和CCD之间安置一滤光片(激光器发出的红光波长为650 nm，其透过率大于90%，而其他波段的光几乎全部滤掉)，减小了环境的影响。同时在激光器和聚光镜之间安置孔径光阑，减小光斑直径[8-10]。

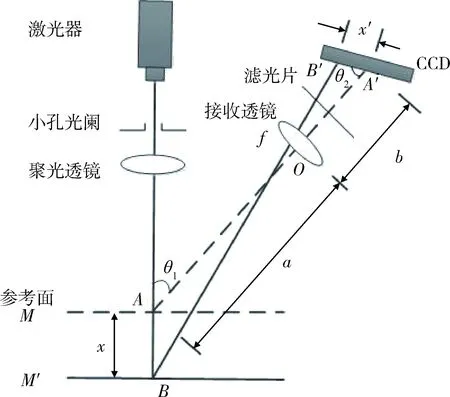
图1 激光三角法测量原理图Fig.1 Measurement principle of laser triangulation

传感器激光束与被测面垂直，只有一个准确调焦的位置，其余位置的像都处于不同程度的离焦状态，离焦引起像点的弥散，降低了系统的测量精度。为了提高测量精度，设计中采用了恒焦光路[11]，满足Scheimpflug条件，即θ1和θ2满足：

(1)

式中：β为接收透镜横向放大率；θ1为激光束与接收透镜光轴之间的夹角；θ2为CCD光敏面与接受透镜光轴之间的夹角。

式(1)表明，成像面、被测物表面和透镜主平面相交于一个共同点，无论被测物表面如何移动，光斑都能在CCD上成清晰的像[12-13]。

当被测表面位于参考面M时，光斑成像于CCD中心位置A′处；当被测面距离参考面M的位移为x，向下移动到M′时，光斑成像于CCD光敏面的B′处，光斑像点在CCD上的位移为x′，设x′=A′B′，利用几何光学的基本知识，可得出被测面沿法线方向的移动距离为

(2)

式中：a为激光束和参考平面M的交点到接收透镜前主面的距离；b为接收透镜后主面到成像面中心点的距离。

通过CCD测量光斑像点的位移，由式(2)可得激光位移传感器到被测物体的距离。

1.2 角度测量系统设计

如图2虚线框内所示，角度测量系统由2个激光位移传感器、信息采集系统、信号同步系统和PC软件构成。为了评价本文角度测量方法的精度，利用高精度转台作为基准获取系统的测量误差。

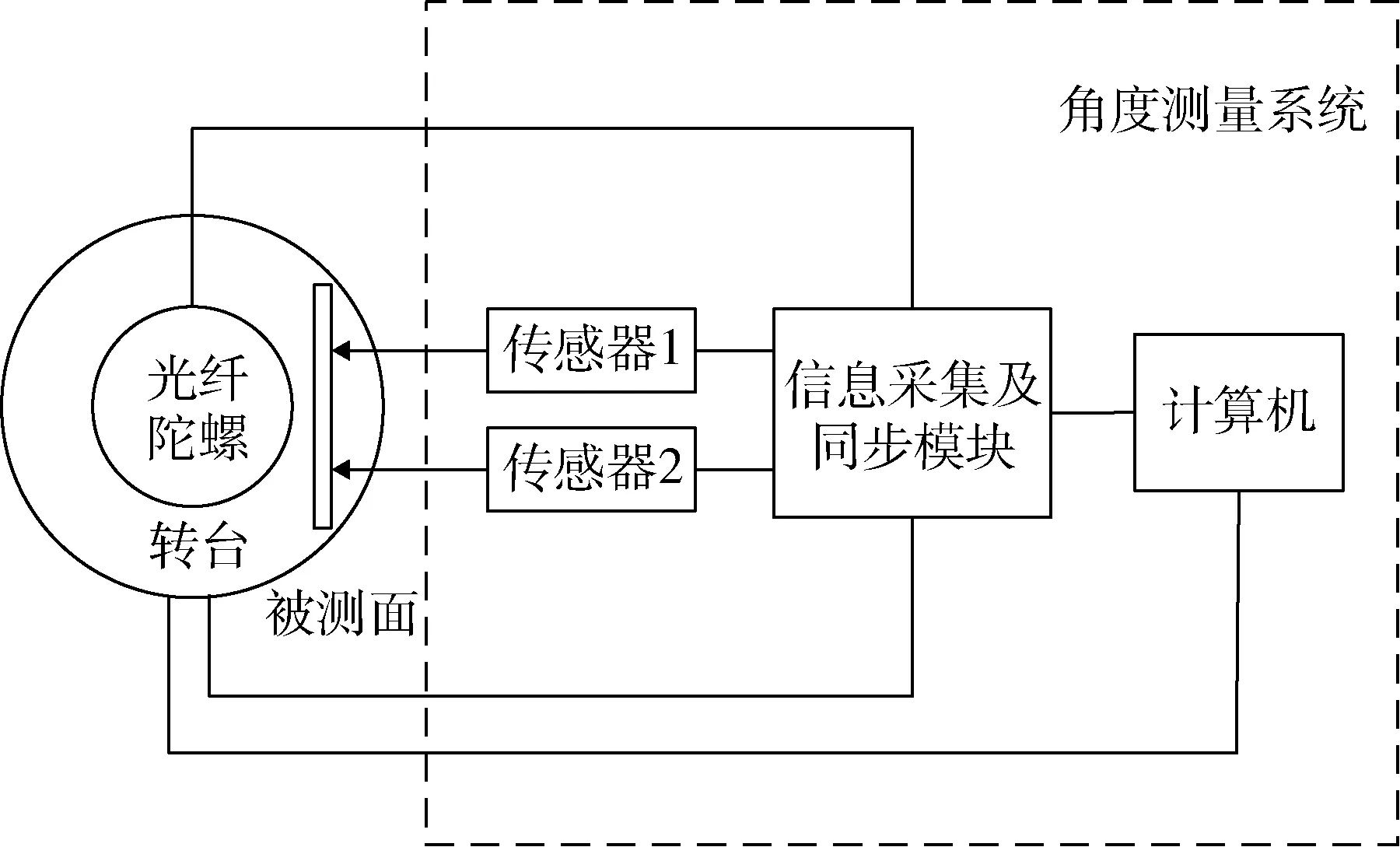
图2 实验总体测量示意图Fig.2 General diagram of the measurement system

实验总体框图如图2所示，将被测面安装在高精度转台上，用计算机控制转台的摆幅和频率，2个激光位移传感器在转台转动的过程中实时测量传感器到被测面的距离，并将测量数据通过信息采集及同步模块实现与转台的输出同步，并将数据发送给计算机进行处理。

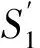
(3)

式中：θ为被测面相对初始垂直位置转过的角度，逆时针为正，顺时针为负。

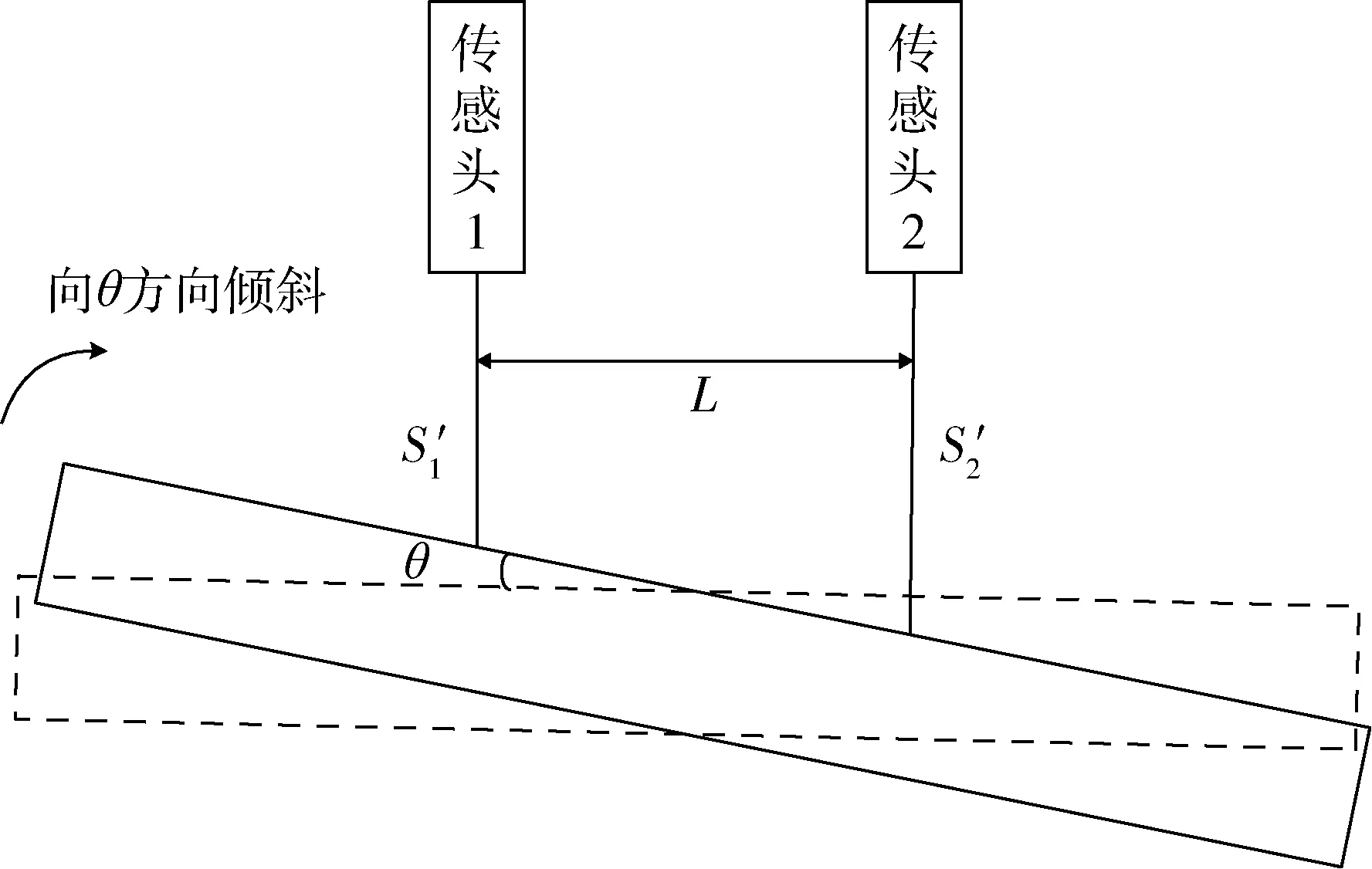
图3 位移与角度的关系Fig.3 Relations of displacement and angle

2 实验结果

图4是所搭建的实验装置，光纤陀螺仪与被测面安装在高精度转台上，陀螺敏感轴与摆动平面垂直；调整2个激光位移传感器，使其发出的光束平行；设置高精度转台的摆动幅度为±10°，摆动频率为1 Hz；计算机采样频率为2 000 Hz。以高精度转台的角位移作为参照，比较激光位移传感器的测量值，得到传感器的角度测量误差。实验测量结果如图5所示。

图4 实验装置图Fig.4 Diagram of experimental device

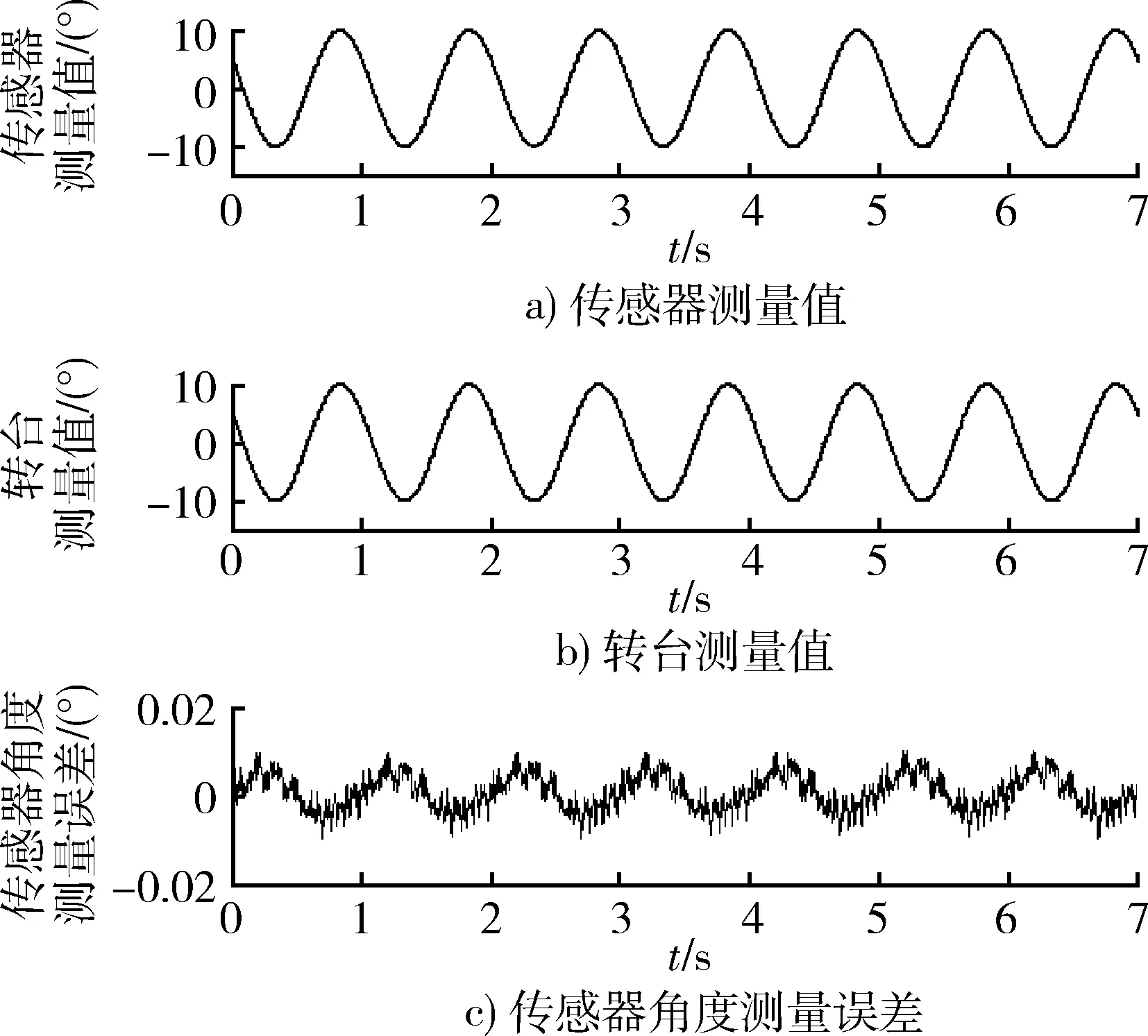
图5 角度测量误差实验结果Fig.5 Diagram of angle measurement result

3 误差分析与补偿

3.1 误差分析

被测面的初始位置与激光位移传感器不垂直和2个激光位移传感器不平行是2个主要影响角度测量精度的因素。

实验中调节被测面与两激光束垂直是将反射镜紧贴被测面，通过调节转台，使两激光束打在反射镜后光路沿原路返回，以此时被测面的位置为初始位置计算角度值，但手动调整垂直存在误差，经计算，初始位置与激光束的不垂直度为0.33°时，对于10°的转角，存在0.010 29°的角度测量误差，误差原因是由于式(3)计算角度的理论前提是两激光束与被测面初始位置垂直，因此必须通过定量计算找到与两激光束垂直的理想初始位置。

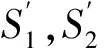
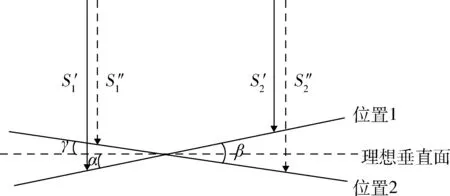
图6 几何示意图Fig.6 Diagram of geometry

如图6所示，根据式(3)可得

(4)

(5)

(6)

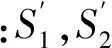
由于逆时针为正，因而γ，β为负，α为正，由图6可知：

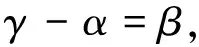
(7)

将式(4)～(6)代入式(7)，可得

(8)

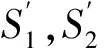
而对于激光位移传感器的不平行误差，主要通过软件补偿方法进行补偿。

3.2 误差补偿

本实验采取多项式拟合方法对实验结果进行误差补偿。多项式拟合方法，又称曲线拟合方法，是以实验数据为基础，用连续曲线在一定意义下近似地刻画或比拟平面上离散点所表示的坐标之间的函数关系，其基本思想就是选择一个多项式函数

(9)

去逼近一组测量数据(xi，yj)，并使多项式函数f(x)同测量数据(xi，yj)的误差的平方和最小[14]。

图7所示为传感器的角度测量误差随转角的变化，由图7可知误差随转动角度的增大而增大，是趋势性误差[15]，建立误差多项式模型为

f(x)=a0+a1x+a2x2+a3x3+a4x4+

a5x5+a6x6+a7x7,

(10)

式中：x为激光位移传感器测量的角度值；a0，a1，a2，a3，…，a7分别为拟合曲线的常数项及一次、二次、三次……七次项系数。

图8所示是对图7的传感器角度测量误差进行最小二乘拟合的拟合曲线，横坐标x代表传感器测量角度，纵坐标f(x)代表角度测量误差的拟合值，由此可得a0=0.001 64，a1=1.82e-04，a2=1.48e-04，a3=-5.47e-05，a4=-3.15e-06，a5=1.17e-06，a6=1.96e-08，a7=-6.92e-09。

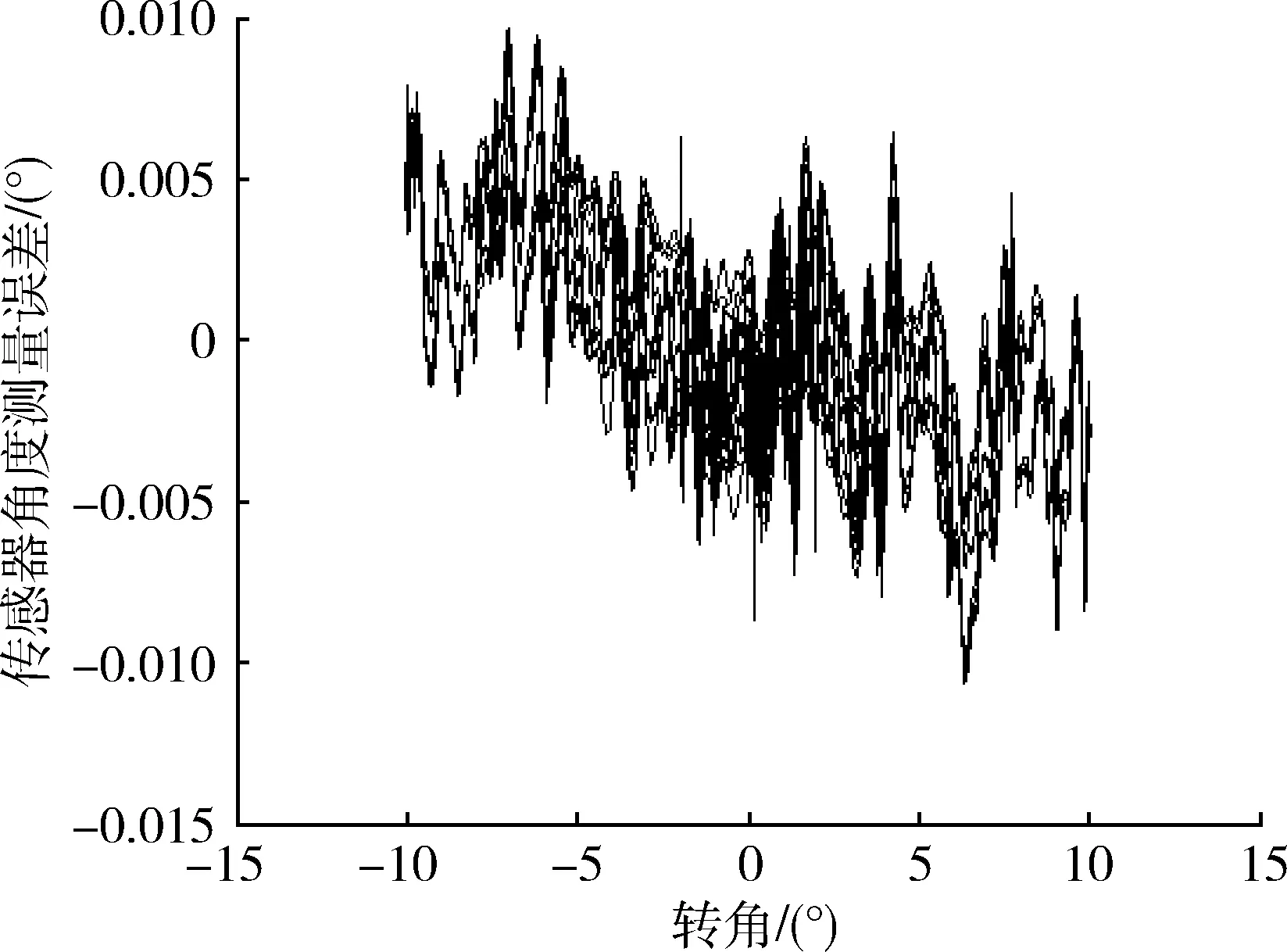
图7 角度测量误差与转角的关系Fig.7 Relation between error of angle measurement and rotation angle

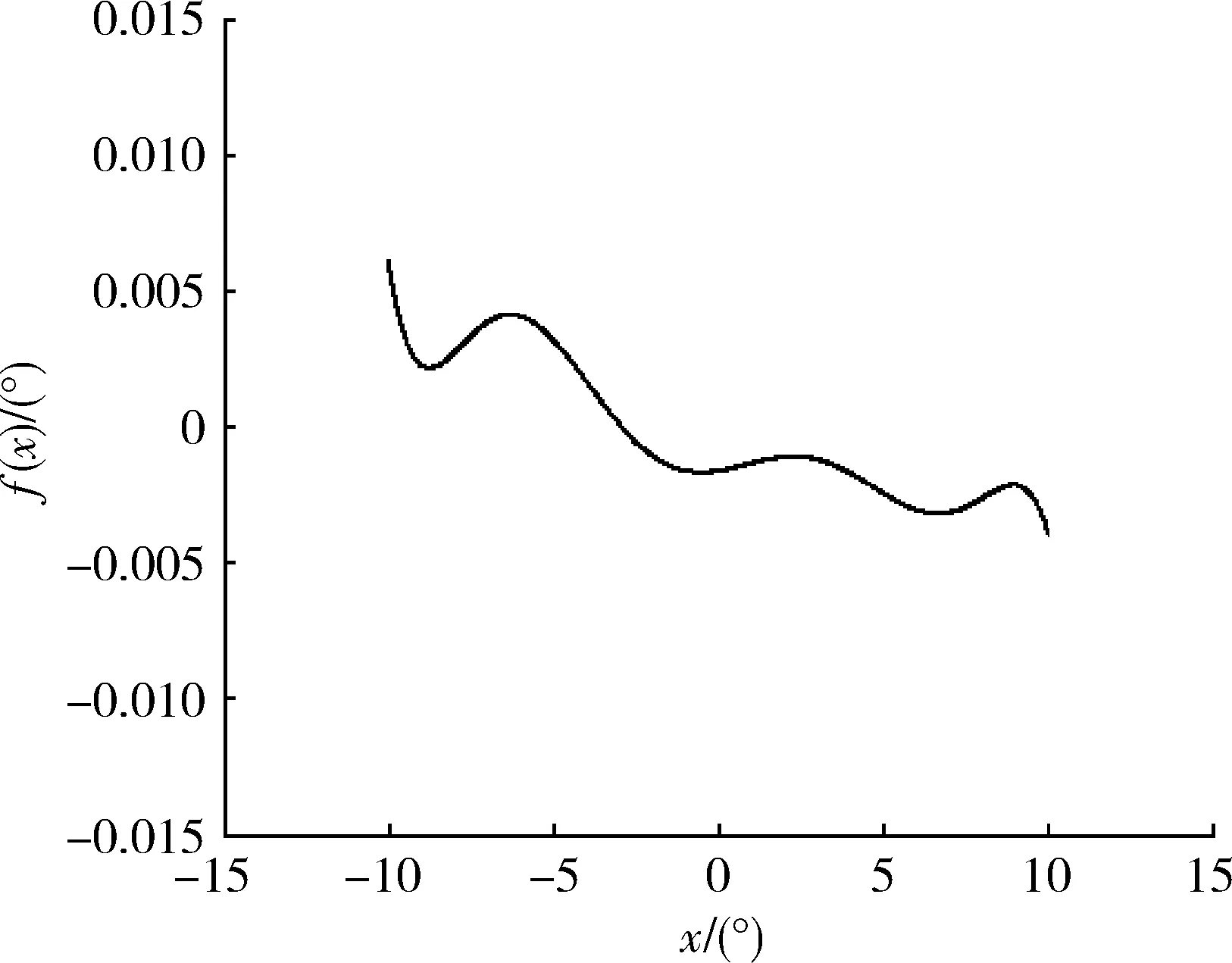
图8 误差模型拟合曲线Fig.8 Fitting curve of error model

图9是补偿后角度测量误差，从图中可知误差由±0.01°降到±0.005°，降低一个数量级，经多次测量，该误差模型满足测量要求。

以上实验以高精度转台作为基准，获取系统的角度测量误差，实验结果证明，本文提出的角度测量系统的误差仅有±0.005°，可用于光纤陀螺的测角误差标定。按图4的实验装置，将此角度测量系统与光纤陀螺的输出同步，对光纤陀螺的测角误差进行标定，得到光纤陀螺的测角误差标定结果如图10所示，图10a)中虚线为激光位移传感器的角度测量曲线(左坐标轴)，实线为光纤陀螺的角度测量曲线(右坐标轴)；图10b)为光纤陀螺的角度测量误差。

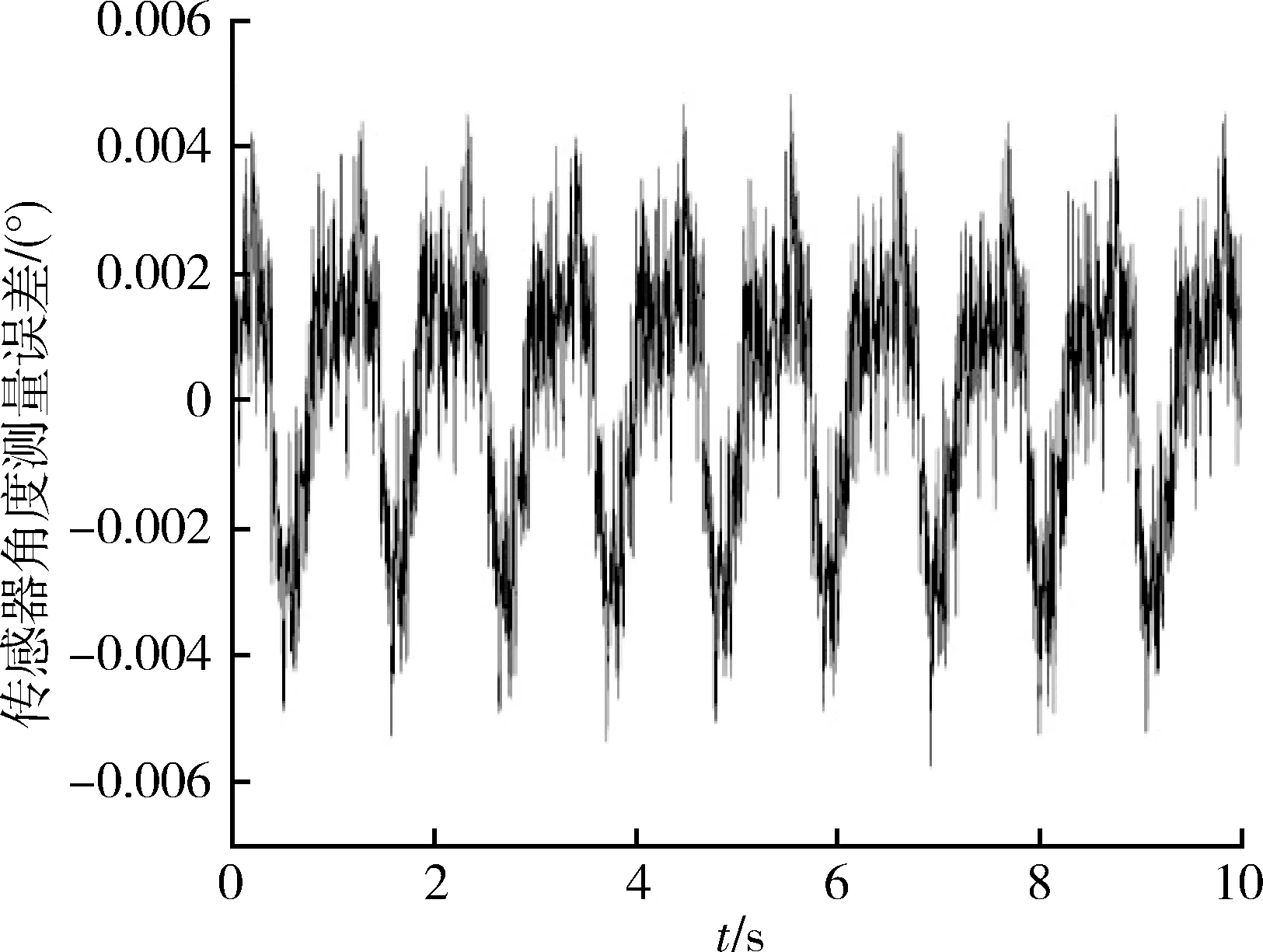
图9 补偿后的角度测量误差Fig.9 Compensated angle measurement error

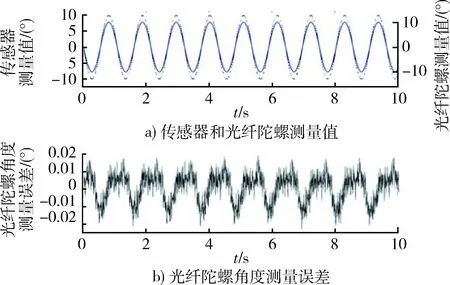
图10 光纤陀螺角度测量标定结果Fig.10 Calibration result of angle measuring of fiber gyro

4 结束语

本文提出了一种新的基于光学三角法的光纤陀螺角度测量误差标定技术，该技术基于非接触光学方法，对被测物体表面的粗糙度和光洁度要求不高，对被测物表面没有损伤。实验证明，这种利用激光位移传感器实现了大范围(±10°)、高精度(±0.005°)的实时角度测量，可用于光纤陀螺在转台或振动台等载体上的测角误差标定。此方案测量方法简单易行，可推广应用到其他测角系统的标定工作中。

[1] 王巍.光纤陀螺惯性系统[M].北京：中国宇航出版社，2010：132-170. WANG Wei.Fiber- Optic Gyroscope Inertial System[M].Beijing：China Aerospace Press，2010：132-170.

[2] SHEN Chong，CHEN Xi- yuan.Analysis and Modeling for Fiber- Optic Gyroscope Scale Factor Based on Environment Temperature[J].Applied Optics，2012，51(14)：2541-2547.

[3] NAYAK J.Fiber- Optic Gyroscopes：From Design to Production[Invited][J].Applied Optics，2011，50(25)：E152-E161.

[4] 太松月.光纤陀螺捷联惯性导航系统标定测试技术研究[D].哈尔滨：哈尔滨工程大学，2007：1-84. TAI Song- yue.Reaserch on Calibration Testing Technology of Strapdown Inertial Navitation System Based on Fiber- Optic Gyroscope[D].Harbin： Harbin Engineering University，2007：1-84.

[5] BARBOUR N，SCHMIDT G.Inertial Sensor Technology Trends[J].IEEE Sensors Journal,2001,1(4):332-339.

[6] 常城，张志峰.激光三角法测量的误差研究[J].中国科技信息，2006(23)：61-64. CHANG Cheng，ZHANG Zhi- feng.Study on the Error in Triangular Laser Measurement[J].China Science and Technology Information，2006(23)：61-64.

[7] 吴剑锋，王文，陈子辰.激光三角法测量误差分析与精度提高[J].机电工程，2003，20(5)：89-91. WU Jian- feng，WANG Wen，CHEN Zi- chen.Study on the Analysis for Error in Tringular Laser Measurement and the Method of Improving Accuracy[J].Mechanical & Electrical Engineering Magazine，2003，20(5)：89-91.

[8] 金洪禹.基于光散射的三角法测量技术的研究[D].哈尔滨：哈尔滨工业大学，2006：1-54. JIN Hong- yu.Based on Laser Trigonometry Measuring Technology Research[D].Harbin：Harbin Institute of Technology，2006：1-54.

[9] 陈浩，吕超，车英，等.物面倾斜对激光三角法测量误差影响的分析研究[J].长春理工大学学报：自然科学版，2015，28(1)：17-20. CHEN Hao，LÜ Chao，CHE Ying，et al.Analysis on the Object Surface Tilt Effect on the Measurement Error of Laser Triangulation Method[J].Journal of Changchun University of Science and Technology：Natural Science ed，2015，38(1)：17-20.

[10] 冯金城.高精度实时激光三角测距系统设计[D].南京：南京理工大学，2008：10-35. FENG Jin- cheng.Design on High Precision Real- Time Laser Triangulation Ranging System[D].Nanjing：Nanjing University of Science and Technology，2008：10-35.

[11] 钱晓凡，吕晓旭，钟丽云，等.提高激光三角法测量精度的新方法[J].激光杂志，2000，21(3)：54-55. QIAN Xiao- fan，LÜ Xiao- xu，ZHONG Li- yun，et al.A Novel Metheod for Improving Measuring Accuracy in Laser Triangle Method[J].Laser Journal，2000，21(3)：54-55.

[12] 冯俊艳，冯其波，匡萃方.高精度激光三角位移传感器的技术现状[J].应用光学，2004，25 (3)：33-36. FENG Jun- yan，FENG Qi- bo，KUANG Cui- fang.Present Status of High Precision Laser Displacement Sensor Based on Triangulation[J].Journal of Applied Optics，2004，25 (3)：33-36.

[13] DANESHPANAH M，HARDING K.Surface Sensitivity Reduction in Laser Triangulation Sensors[J].Proc.of SPIE，2011(8133)：81330O- 81330O- 9.

[14] 文香稳.盾构姿态测量中的倾角仪误差补偿研究[D].武汉：华中科技大学，2011：1-29. WEN Xiang- wen.Research on Error Compensation of Inclinometer in Pose Measurement of Shield Machine[D].Wuhan：Huazhong University of Science and Technology，2011：1-29.

[15] 张京娟，张仲毅，刘俊成.一种新型的旋转变压器测角误差标定技术[J].仪器仪表学报，2010，31(1)：149-152. ZHANG Jing- juan，ZHANG Zhong- yi，LIU Jun- cheng.Novel Method of Calibrating the Angle- Measurement Error of Resolver[J].Chinese Journal of Scientific Instrument，2010，31(1)：149-152.

One- Dimensional Angle Measurement Error Calibration Technique for Fiber Optic Gyroscope

YANG Meng- fanga，CHEN Leia，TIAN Huib，ZHANG Deng- weia， SHU Xiao- wua，CHE Shuang- lianga

(Zhejiang University，a.College of Optical Science and Engineering,State Key Laboratory of Modern Optical Instrumentation；b.School of Medicine,Women’s Hospital，Zhejiang Hangzhou 310027，China)

As the angle measuring error of fiber optic gyroscope increases cumulatively under the condition of long- term operation, a new error calibration method is proposed for fiber optic sensor. The method is based on the principle of optical triangulation distance measurement, using data acquired by two laser displacement sensors to realize the real- time angular measurement, and the experimental verification of the measurement system is carried out on the high- precision turntable. Experimental results show that the range of angle measurement can be up to ±10°, while the error is about ±0.005° through compensating the error by least square fitting method, which provides the basis for exact estimate of angle measuring precision of gyro. The non- contact optical measurement method used has no damage to the surface to be measured.

fiber optic gyroscope； error calibration； laser triangulation method；angular measurement； non- contact measurement； real time

2016-08-31；

2017-02-01 基金项目：国家自然科学基金(61203190)；浙江省自然科学基金(LY17F030010) 作者简介：杨梦放(1993-)，女，河南辉县人。硕士生，主要从事光纤传感技术的研究。

10.3969/j.issn.1009- 086x.2017.04.003

V241.5；TN253

A

1009- 086X(2017)- 04- 0011- 06

通信地址：100854 北京市142信箱30分箱 E- mail：ymfzju@163.com