绕回转航行体通气空泡末端泄气模式研究

孔德才，裴金亮，于海涛，李 岩

绕回转航行体通气空泡末端泄气模式研究

孔德才，裴金亮，于海涛，李 岩

（北京宇航系统工程研究所，北京，100076）

通过布置在水下回转航行体表面的排气缝向已有自然空泡内通气，形成通气空泡，可改善航行体所受流体动力。基于试验研究和数值计算方法，分析通气空泡在傅汝德数（重力）、通气率共同影响下的形态特征和稳定性机理。结果表明，在不同傅汝德数和通气率下，空泡呈现两种不同的流动状态：一种是空泡在航行体表面不闭合，在回转航行体上部形成对涡结构，末端呈涡管状泄气模式；另一种是空泡末端闭合在航行体表面，形成反向回射流，在回射流的切割作用下，空泡会出现断裂和脱落，空泡呈非定常发展，末端呈回射流闭合模式。研究结果为水下航行体流体动力控制方法设计提供指导。

回转航行体；通气空泡；回射流；稳定性

0 引 言

航行体水下高速运动过程中，通过布置在航行体表面的排气缝向已有自然空泡内通气，提高空泡内压力，增加空泡在航行体表面覆盖面积。由于气体的密度、粘性远小于水，采用通气空泡手段，有助于降低航行体阻力，提高航行体速度和稳定性。因此通气空泡在水下高速航行体的应用非常广泛，早在1946年，Reichardt提出了人工通气形成空泡的方法[1]。

基于Logvinovich[2,3]理论，张学伟[4]等人提出一种用于计算非定常通气空泡形态的方法，对空泡形态的稳定性进行了数值计算研究；陈伟政[5]等对重力场作用下轴对称体稳定空泡形态开展了试验研究。相关研究结果表明，重力和通气率对空泡形态存在较大影响，本文结合水洞试验和数值计算方法，对不同傅汝德数（重力影响）、通气率影响下的绕回转航行体空泡变化规律进行研究，获得了回射流泄气模式下的空泡稳定性机理。

1 试验模型

试验在北京理工大学高速循环空化水洞中进行，试验装置的具体参数和试验观测系统介绍见文献[6]。试验中采用钝锥头体的回转航行体模型，航行体直径为20 mm，在航行体柱段前部设置1 mm的通气缝，模型通过侧支撑水平固定在水洞试验段，气体由侧支撑内的管路进入回转航行体内经通气缝排出，形成通气空泡。

试验模型在水洞中的安装示意如图1所示。

图1 水洞试验装置实验段及回转航行体安装位置

影响通气空泡两相流流场结构的因素主要包括来流速度和通气量。为了研究各参数对通气空泡流动的影响，定义如下2个无量纲数：

式中 Qin为通气流量；U∞为无穷远来流平均速度（速度剖面充分均匀）；S0为通气面积；L0为通气特征长度，取；g为重力加速度。试验过程中环境压强为101.3 kPa，0.18≤Qv≤0.34；4.5≤Fr≤21.7。

2 计算模型

2.1 控制方程

本文采用均质平衡流模型，气、液两相流的连续性方程和动量方程如下：

式中 下标i和j分别代表坐标方向；mρ，u和p分别为混合密度、速度和压强；μ，tμ分别为混合介质的层流和湍流黏度；lρ，gρ分别为水和气体的密度；lα，gα分别为多相流中水和气体所占的体积分数。

2.2 湍流模型

本文采用标准k-ε湍流模型，控制方程为

式中 Pt为湍动能生成项；ijτ为雷诺应力张量；k，ε分别为湍动能和湍流耗散率；tμ为湍流粘性系数。模型常数分别为：1Cε=1.44，2Cε=1.92，εσ=1.92，kσ=1.0。湍流粘性系数tμ定义为

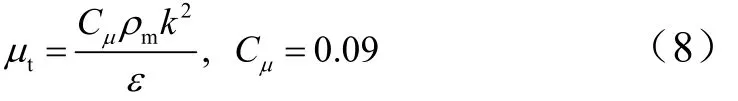
式中tμ与mρ呈线性关系。

2.3 空化模型

忽略热传输和非平衡相变效应，采用组分传输方程空化模型描述水相体积含量的输运方程为

式中 m˙+和m˙−分别为考虑蒸发和凝结的源项。根据Rayleigh-Plesset方程描述空泡的增长和溃灭过程，不同空化模型源项的表达形式不同。

本文采用Singhal模型，该模型是由Singhal[7]等在Rayleigh-Plesset气泡动力学方程的基础上得到的。通过假设来流中存在单位体积密度为n的气核，推导出密度随时间的变化率与蒸汽分数αv、气泡半径变化率dR/dt、平均气泡大小等参数之间的关系，进而在做了一些合理假设的基础上，得到如下描述蒸发和凝结的质量源项：

式中 Ce和Cc为经验常数，本文中取Ce=0.02，Cc=0.01；Vch为一特征速度，表征液相和汽相的相对速度，Singhal模型认为，此相对速度与湍流脉动速度为同一量级，所以在计算中，近似地取；σ为液体的表面张力系数。

2.4 几何模型和边界条件

采用结构化网格对本文的计算域进行划分，回转航行体表面和通气缝位置处进行网格加密，总网格量为2.2×106。远场入口条件定义为速度入口，设定值为来流速度；出口条件定义为压力出口，设定值为当地的静压；回转航行体表面定义为壁面条件；通气缝出口定义为速度入口，根据试验通气率进行换算。

3 回转航行体通气空泡形态发展过程

基于高速循环水洞，利用高速全流场显示系统获得不同傅汝德数和通气率下的空泡形态，对应地开展相同工况下的数值计算研究（见图2）。对比分析可知，在不同的来流条件下，空泡呈现出2种形态：a）在重力作用下，通气空泡上漂形成涡带，并不断向下游泄气；b）空泡闭合在航行体表面，形成闭合空泡。

图2 典型状态下的空泡形态（左为试验结果，右为计算结果）

由图2可知，Qv为0.18时，空泡形态表明，随着Fr的增加，重力对空泡形态的影响减弱，空泡由涡带泄气模式向空泡闭合模式转变，在空泡末端回流的作用下，空泡逐渐由透明状转变为雾状。

Fr=21.7时，随着Qv的增加，通入流场中的气量增加，空泡长度增加，空泡形态基本一致，末端均闭合在航行体表面。空泡末端的回流至空泡内部，汽水掺混使得空泡界面呈云雾状。

4 不同空泡形态下的流场结构

涡带泄气空泡流场结构如图3所示，闭合空泡流场结构如图4所示。

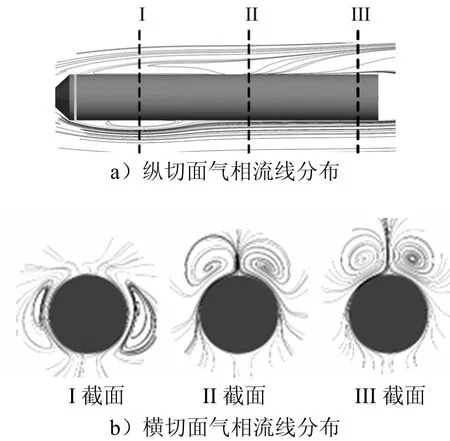
图3 涡带泄气空泡流场结构（Fr＝4.5，Qv＝0.18）

图4 闭合空泡流场结构（Fr＝21.7，Qv＝0.18）

为了进一步对不同空泡形态下的流场结构进行分析，提取了航行体纵切面气相流线分布，如图3a和图4a所示，并在航行体轴线方向取Ι、ΙΙ、ΙΙΙ 3个横向截面（分别距航行体顶端2d，4d和6d），如图3b和图4b所示。由图3可知，在涡带泄气模式下，通入气体在浮力作用下上漂，在航行体表面未形成闭合点，上漂的气体形成一对漩涡，气体通过这一涡结构不断泄出。由图4可知，在闭合空泡形态下，在空泡末端形成了回流，在回流的作用下，空泡变得混浊，呈现明显的气、水掺混状，气体未出现明显的上漂，有效地控制了气体的泄出。

5 回射流泄气模式下的空泡稳定性

通过水洞试验观测到，回射流模式下，空泡内部气、水存在明显的掺混，气液界面不清晰，在空泡的末端存在不稳定空泡云团脱落，如图5所示。空泡脱落后，回射流重新在航行体表面闭合，并沿航行体表面继续推进，当空泡生长到一定尺度后，在回射流的切割作用下再次发生脱落，以此往复，呈现非定常周期性特性。

图5 空泡末端云团脱落

图6 空泡末端回射流动结构

在回射流模式下，由数值计算方法得到的空泡形态和航行体表面的速度矢量见图6。由图6可知，空泡末端闭合于航行体表面后，在空泡区和末端沾湿区逆压梯度的作用下，在空泡尾部形成反向回射流动，回射流沿航行体表面向前部推进，当回射流到达空泡前部时与通入的空气掺混，且撞击切割空泡壁面，附近空泡赖以存在的低压区受到破坏，空泡便出现不稳定性的断裂现象并脱离航行体表面。

6 结 论

本文基于循环高速水洞试验和数值计算方法，分析了绕回转航行体通气空泡形态特征及其影响因素，得到以下结论：

a）绕回转航行体通气空泡有涡管泄气和回射闭合两种模式，当傅汝德数较小时，重力对空泡形态起主导作用，空泡上漂，在回转航行体上部形成对涡结构，气体不断泄出，空泡呈涡管泄气模式；随着傅汝德数增加，重力对空泡形态的影响逐渐减小，空泡末端闭合在回转航行体表面，形成回射流，汽水掺混，空泡内呈云雾状；

b）在空泡闭合状态下，反向射流由空泡末端向前部推进，当回射流流动与空泡壁面相撞时，破坏了空泡的稳定性，空泡出现断裂现象并在前方水流的冲刷作用下向航行体尾部脱落。

[1] Reichard H. The laws of cavitation bubbles as axially symmetrical bodies in a flow[C]. Russian: Ministry of Aircraft Productuin(Great Britian), 1946.

[2] Logvinovich G V. Hydrodynamics of flow with free boundaries [M]. Kiev: Naukova Dumka, 1969.

[3] Savchenko Y N, Vlasenko Y D, Semenenko V N. Experimental study ofhigh-speed cavitated flows [J]. Ιnter-national Journal of Fluid Mechanics Research, 1999, 26(3): 365-374.

[4] 张学伟, 等. 通气超空泡稳定性分析的一种数值算法[J], 力学学报, 2008, 40(6): 820-824.

[5] 陈伟政, 张宇文, 袁绪龙, 邓飞. 重力场对轴对称体稳定空泡形态影响的实验研究[J]. 西北工业大学学报, 2004, 22(3): 274-278.

[6] 黄彪, 王国玉, 王复峰, 等. 非定常空化流场结构实验研究[J]. 实验力学, 2011, 26(4):417-424.

[7] Singhal A K, Athavale M M. Mathematical basis and validation of the full cavitation model[J]. ASME Journal of Fluids Engineering, 2002, 124: 617-624.

Research on Gas Leakage Mechanism of Ventilated Cavitating Flows Around An Axisymmetric Body

Kong De-cai, Pei Jin-liang, Yu Hai-tao, Li Yan
(Beijing Ιnstitute of Astronautical Systems Engineering, Beijing, 100076)

Ventilated cavity formed by the gas which vent through the air gap which set on the submarine vehicle. Base on experiment and numerical simulation, this paper studies the shape and stability of the cavity influenced by Fr and ventilation rates. There are two flow states of the ventilated cavity. The first state is that the ventilated cavity doesn’t closed on the axisymmetric body, form vortex structures on the upper part of axisymmetric body, the gas leakage from the tail of the cavity in the mode of vortex-pipe; the second state is that the ventilated cavity closed on the axisymmetric body, and he re-entry jet formed at the end of the ventilated cavity, the gas and water fixed in the internal of the ventilated cavity, the ventilated cavity become instability as the re-entry jet strike on the surface of the ventilated cavity the gas leakage from the tail of the cavity in the mode of closed re-entry.

Axisymmetric body; Ventilated cavity; Re-entry jet; Stability

V414.3+1

A

1004-7182(2017)04-0013-04 DOΙ：10.7654/j.issn.1004-7182.20170404

2016-12-15；

2017-06-08

孔德才（1983-），男，高级工程师，主要研究方向为水下航行体非定常水动力特性