大功率发动机活塞蠕变-疲劳可靠性分析方法研究
赵 丹, 刘 勤, 刘 英, 李 娟
(中国兵器工业质量与可靠性研究中心, 北京 100089)
【装备理论与装备技术】
大功率发动机活塞蠕变-疲劳可靠性分析方法研究
赵 丹, 刘 勤, 刘 英, 李 娟
(中国兵器工业质量与可靠性研究中心, 北京 100089)
针对大功率发动机活塞在周期性爆发压力、活塞销反力、高温及循环热载荷复杂工况下经常出现的蠕变-疲劳故障现象,通过试验和数值模拟方法研究材料、高温等因素对蠕变-疲劳故障的影响规律,提出基于故障物理的机械可靠性设计分析技术,以故障机理为单元,分别建立蠕变、疲劳及其交互作用的损伤模型,利用损伤等效方法建立基于线性损伤累积的活塞蠕变-疲劳可靠性模型,对活塞可靠度、灵敏度和可靠寿命进行了分析计算,并对计算方法进行了对比验证,计算结果与传统蒙特卡洛法计算结果接近,但计算量明显减少。
活塞;蠕变-疲劳故障;可靠性分析;故障物理;损伤等效
为满足新一代主战坦克和新概念未来作战系统对高紧凑、轻量化推进系统的需求,国内外均在积极发展高功率密度发动机,以德国MTU890发动机为例,其单位体积功率达到1 358 kW/m3,而单位功率质量仅0.94 kg/kW,与相同功率的普通发动机相比,质量和体积减小约60%。活塞是发动机中直接承受热载荷和机械载荷综合作用的运动部件之一,其工况恶劣,失效机理复杂。在发动机试样研制、试验过程中出现多起活塞连杆组故障,尤其在高原、高热区域使用时,更为突出。对于大功率发动机活塞,随着其功率密度和转速的不断提高,活塞头部位置的最高温度达到350~400 ℃,所承受的最大爆发压力达到22 MPa[1-2]。活塞在高温长期作用下,不仅容易发生疲劳失效[3-5]其蠕变的影响不可忽视[6],如某发动机活塞产生头部裂纹。活塞不仅承受周期性变化的爆发压力、活塞销反力等作用,并且处于高温和循环热负荷状态,其故障机理为疲劳与蠕变造成活塞内部损伤[7-8],且蠕变损伤的微孔洞生长与疲劳损伤的微小裂纹存在耦合作用,影响活塞寿命。
1 蠕变-疲劳故障影响因素分析
根据蠕变-疲劳故障的发生机理,本文从材料力学性能、高温及载荷等几个方面对蠕变-疲劳故障的影响因素分析。
1.1 材料力学性能
高温下材料的力学和疲劳特性往往会发生急剧蜕化。为了研究高温环境对材料性能的影响,对发动机活塞常用材料铝合金试样做拉伸试验。图1为材料力学参数随温度的变化情况。
由图1可以看出,材料的性能参数均具有分散性,因此在对活塞进行靠性分析时,材料性能参数的随机性是不可忽略的[9]。此外,随着温度的升高,材料在高温下微观组织发生的变化[10-11],材料抵抗蠕变-疲劳的能力降低,产品寿命缩短。
1.2 高温蠕变影响
为了研究高温对结构蠕变的影响,选择拉伸试样为研究对象,分别对环境温度为200℃、300℃和400℃,机械载荷P为0.3σb、0.5σb、0.7σb进行了有限元数值模拟试验,测定了40 min(2 400 s)内蠕变变形情况。
图2为各试验温度及不同载荷下,试样最大应变节点蠕变应变随时间的变化曲线。由图2可以看出,随着时间的增长,蠕变速率减慢,呈现出过渡蠕变和稳态蠕变典型的两阶段特征[12]。随着温度的升高,同一时刻材料的蠕变应变增加,材料抵抗蠕变变形的能力大幅下降。图2(a)、图2(c)比较可知,高温环境下材料的蠕变变形对机械载荷十分敏感,环境温度为400 ℃,机械载荷由0.2σb~0.7σb时,蠕变应变增长5倍以上。随着机械载荷、特别是温度的增加,蠕变变形的大小呈指数、幂指数的关系增长[13]。
通过对蠕变-疲劳故障影响因素的分析可知,对活塞进行可靠性分析时,应重点考虑活塞材料性能、工作温度及载荷工况等因素。可靠性建模过程中,考虑到材料蠕变、疲劳特性与活塞构件存在差异,在此参考机械设计手册对其进行了修正。

图1 不同温度下的活塞材料力学性能参数
2 基于损伤等效的活塞蠕变-疲劳可靠性建模
在蠕变-疲劳故障机理作用下,研究零部件寿命的方法主要有3种[14]:第1种认为蠕变和疲劳互不影响,分别独立进行疲劳寿命和蠕变寿命的计算,选择两种结果的较小数值,但所得结果与实际相差较大。第2种以疲劳或蠕变为主,将另一个故障机理作为影响因素。该计算方法计算简单,适用于失效模式主次影响分明,耦合作用较小的情况。第3种将蠕变和疲劳同等对待,考虑它们对零部件损伤的共同作用及相互影响,这种方法能客观全面的考虑蠕变-疲劳对零部件破坏的作用。

图2 高温和载荷对蠕变变形的影响

图3 蠕变-疲劳损伤等效模型构建流程
通过对活塞蠕变-疲劳故障机理及影响因素的分析,本文借鉴第三种方法,针对发动机活塞结构发生的蠕变-疲劳故障,在分别研究单一故障机理和交互作用损伤模型基础上,利用损伤等效方法建立蠕变-疲劳可靠寿命模型,建模流程如图3所示。
2.1 蠕变损伤模型
由于活塞材料参数具有一定的分散性,将其视为随机变量,利用Box-Behnke方法取样,生成样本,通过ANSYS进行蠕变分析,获得活塞蠕变变形结果。利用最小二乘法你和蠕变相应面系数,确定蠕变的响应面函数,如式(1):
εc=2×10-7×P+4×10-10×E+13.65×α+6.97×10-9×β+2.48×10-4×c1-2.57×10-8×c2-2.1×10-9×P×E+4.4×10-4×E×α+6.9×10-6×P×c1+6.4×10-10×β×c1-1.7×10-3×α×c2+1.0×10-5
(1)
式(1)中,E为弹性模量;α为线膨胀系数; β、c1、c2为蠕变参数。
假设一个发动机启动-稳定-停止循环,平均为2h。则每个启动-稳定-停止循环,活塞的蠕变损伤dDc为
(2)
2.2 疲劳损伤模型
根据发动机运行工况及活塞通常发生的低周疲劳,疲劳损伤Df可借助于Manson-Coffin公式计算[15]。对于平均应变不为零的情况,采用工程上广泛应用的莫罗(Morrow)修正公式:

2.3 蠕变、疲劳交互作用损伤模型
蠕变、疲劳交互作用dDfc以疲劳损伤、蠕变损失和交互作用系数表示:
(5)
式(5)中,B为交互作用系数,与材料、温度等有关。通过进行疲劳、蠕变试验,统计确定交互作用系数B为0.187,B>0说明疲劳、蠕变的交互作用促进损伤累积。
2.4 活塞蠕变-疲劳可靠性模型
针对活塞工作过程中发生的蠕变-疲劳故障,本文采用故障机理可靠性分析方法,以故障机理为单元,通过线性累积方式构建蠕变-疲劳总损伤模型
dD=dDf+dDc+dDfc
(6)
依据发动机耐久性试验规范,试验总时间1 000h,相当于500次启动-稳定-停止循环。根据损伤累积准则,总损伤累积至1时,活塞发生故障,由此建立极限状态函数:
(7)
3 活塞可靠性求解及方法验证
3.1 活塞结构及工况
活塞连杆组是装甲车辆发动机的传动件,把燃烧气体的压力传递给曲轴,是直接承受火力的运动组件。由于工况恶劣,在发动机研制、试验过程中活塞连杆组出现过多起故障。活塞连杆组主要由活塞环、活塞、连杆、活塞销、连杆螺栓等零部件组成,其组成结构如图4所示。

图4 活塞连杆组结构示意图
活塞作为重要组成部件,在工作时头部承受很高的燃气爆发压力作用,大功率发动机缸内最大爆发压力高达22 MPa。活塞头部与缸内的高温燃气直接接触,最高工作温度达350~400 ℃。在发动机启停循环时,循环的机械应力和高温环境作用造成活塞内部产生损伤,发生蠕变-疲劳故障。
3.2 活塞可靠度灵敏度求解
根据活塞可靠性模型(式(7)),利用一次二阶矩法,可得活塞的可靠度为0.997,失效概率为3‰。各随机变量对活塞可靠度的灵敏度如图5所示。材料抗拉强度σb、蠕变参数c1、断裂延性εf对活塞可靠度影响的灵敏度较高,在结构设计改进时,应重点从这3个参数及其随机性方面考虑。
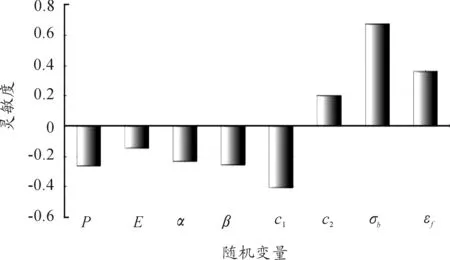
图5 活塞可靠性灵敏度
3.3 活塞可靠寿命求解
分别计算N0=700、800、900、1 000、1 100、1 200、1 300、1 400、1 500、1 600、1 700时活塞的可靠度,以曲线描述活塞可靠度、失效概率与寿命的关系,如图6所示。
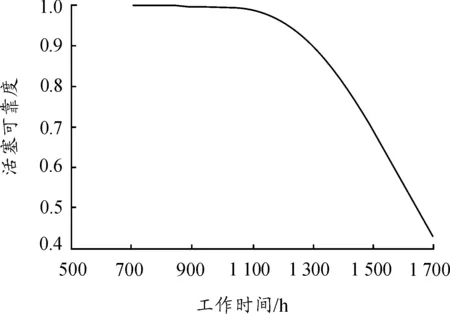
图6 活塞可靠度-寿命关系
通过曲线插值,能够确定任意给定可靠度的活塞寿命。例如,需要计算可靠度为0.5的活塞寿命时,可以通过活塞可靠度-寿命关系图插值得到其可靠寿命约为1 600 h。即经历大概800次启动-工作-停止循环,有一半活塞发生蠕变-疲劳故障。
3.4 计算结果验证分析
为了验证本文蠕变-疲劳可靠寿命计算方法,分别用传统蒙特卡洛法和本文方法计算可靠度为0.9时的活塞寿命,本文方法计算一次需要进行7次迭代,绘制可靠度-寿命插值图共需迭代77次。结果如表1所示。

表1 活塞可靠寿命计算结果
由表1可看出,本文计算方法与传统蒙特卡洛法计算结果近似,计算量明显减少。
4 结论
1) 基于损伤等效的蠕变-疲劳可靠性模型给出了蠕变损伤与疲劳损伤耦合作用的数学关系,客观全面的反映了蠕变-疲劳故障的损伤累积过程。
2) 材料抗拉强度σb、蠕变参数c1、断裂延性εf对发动机活塞可靠度影响的灵敏度较高,在结构设计改进时,应重点考虑这几个参数及其随机性,提高活塞的可靠性。
3) 蠕变-疲劳可靠寿命计算方法的结果与传统蒙特卡洛模拟法计算结果接近,计算量大幅减小,提高了计算效率。
[1] PETER KEMNITZ, OLAF MAIER, RALPH KLEIN. Monotherm, A New Forged Steel Piston Design for Highly Loaded Diesel Engines[C]//SAE Paper 2000-01-0924,2000.
[2] 马学军,马呈新,郭伟.适应欧III要求的柴油机活塞结构设计[J].山东内燃机,2006( 2):11-13.
[3] FLOWEDAY G,PETROV S,TAIT R B.Thermo-mechanical fatigue damage and failure of modern high performance diesel pistons[J].Engineering Failure Analysis,2011,18(7):1664-1674.
[4] 张俊红,何振鹏,张桂昌,等.柴油机活塞热负荷和机械负荷耦合研究[J].内燃机学报,2011,29(1):78-83.
[5] SROKA Z J.Thermal load of tuned piston[J].Ar-chives of Civil and Mechanical Engineering,2012,12(3):342-347.
[6] 张卫正.内燃机受热件热疲劳试验与寿命预测[D].北京:北京理工大学,2002.
[7] 张俊善.材料的高温变形与断裂[M].北京: 科学出版社,2007.
[8] 田素贵,周惠华. 一种单晶镍基合金的高温蠕变损伤[J].金属学报,2003,12(2):22-25.
[9] 刘勤,孙志礼,涂红茂,等.基于单循环功能度量法的结构可靠寿命优化设计[J].兵器装备工程学报,2016(6):6-9.
[10]KASPRZAK W, EMADI D, SAHOO M,et al. Development of aluminum alloys for high temperature[J]. Materials Science Forum, 2009, 618(s1-4): 595-600.
[11]HUMBERTJEAN A, BECK T. Effect of the casting process on microstructure and lifetime of the Al-piston-alloy AlSi12Cu4Ni3 under thermo-mechanical fatigue with superimposed high-cycle fatigue loading[J]. International Journal of Fatigue, 2013, 53(5): 67-74.
[12]余寿文,冯西桥. 损伤力学[M]. 北京: 清华大学出版社, 1997.
[13]张卫正,魏春源,苏志国,等.内燃机铝合金活塞疲劳寿命预测研究[J].中国机械工程,2003,14(10):865-867.
[14]张卫正.内燃机受热件热疲劳试验与寿命预测[D].北京:北京理工大学,2002.
[15]吴波,丛茜,杨利等.具有仿生条纹结构的内燃机活塞疲劳特性回归分析[J].农业工程学报,2016,32(4):48-55.
(责任编辑 周江川)
Research on Creep-Fatigue Reliability Analysis Method of High Power Engine Piston
ZHAO Dan, LIU Qin, LIU Ying, LI Juan
(Quality and Reliability Center of China North Industries Group Corporation, Beijing 100089, China)
The piston of high power engine worked in the environments of periodic explosion pressure, piston pin reaction, high temperature and cyclic thermal. In order to study the creep-fatigue failure frequently appeared on the piston, the influence law of material and high temperature were studied by experiment and numerical simulation. A reliability design analysis method based on fault physics was put forward. Failure mechanism was treated as a unit. The damage models of creep, fatigue and their interaction were established respectively. The creep-fatigue reliability model of piston was established based on the linear damage accumulation method. The reliability, sensitivity and reliable life of piston were analyzed and calculated. And calculation method was compared with Monte Carlo method. Calculation results are Similar, but amount of calculation is obviously reduced.
Piston; creep-fatigue failure; reliability analysis; fault physics; Damage equivalent
2017-05-12;
2017-06-23 基金项目:武器装备预先研究项目(51319010103)
赵丹(1984—),女,硕士研究生,工程师,主要从事武器装备机械可靠性研究。
10.11809/scbgxb2017.08.014
format:ZHAO Dan, LIU Qin, LIU Ying, et al.Research on Creep-Fatigue Reliability Analysis Method of High Power Engine Piston[J].Journal of Ordnance Equipment Engineering,2017(8):58-62.
TP202.1;TJ81
A
2096-2304(2017)08-0058-05
本文引用格式:赵丹, 刘勤, 刘英,等.大功率发动机活塞蠕变-疲劳可靠性分析方法研究[J].兵器装备工程学报,2017(8):58-62.

