纵向振动对捷联惯导误差影响半解析表达式研究

杨 其,苏国华,刘庆宝,刘新学

(1.火箭军工程大学 士官学院， 山东 青州 262500； 2.火箭军装备研究院， 北京 100085；3.火箭军工程大学 初级指挥学院， 西安 710025)

【装备理论与装备技术】

纵向振动对捷联惯导误差影响半解析表达式研究

杨 其1,3,苏国华2,刘庆宝1,刘新学3

(1.火箭军工程大学 士官学院， 山东 青州 262500； 2.火箭军装备研究院， 北京 100085；3.火箭军工程大学 初级指挥学院， 西安 710025)

针对实际动态工况条件下捷联惯导输出与静态条件下输出存在一定误差的问题，在仅考虑纵向振动的条件下，将飞行器仪器舱内的惯导系统等效为杆与阻尼弹簧振子的组合系统，利用复模态分析方法使方程解耦，并推导了动态扰动环境中惯导加速度响应的半解析表达式，给出了实际敏感加速度的包络范围，指出捷联惯导加速度计敏感值变为围绕真实值分布的随机变量是动态环境条件下产生加速度误差的根本原因之一。

纵向振动；捷联惯导；加速度计；动态误差

从材料力学角度来看，固连于飞行器仪器舱的捷联惯导不可能以绝对刚体运动反映出飞行器的运动状态[1,2]，大量试验和仿真表明捷联惯导静态实验室环境下的输出与动态条件下的输出存在一定误差[3-5]，在导航解算算法默认惯导输出完全准确的前提下，从本质上就产生了测量误差。更为科学的方法应该将其考虑为组合线弹性系统，考虑在飞行器飞行过程中受到附面层压力波动等随机输入时线性系统的响应输出。研究在仅考虑纵向振动的情况下，将捷联惯导等效为杆与阻尼弹簧振子组合线性系统，分析随机输入时捷联惯导加速度计误差的形成机理。

1 等效模型描述

捷联惯导在设计安装过程中，为了尽量减小外界振动对仪器带来误差并确保使用中正确安装，一般设计有橡胶垫和安装支架等系统，其安装方式如图1所示。

图1 捷联惯导安装示意图

工程实际中采用的安装方式在理论上具有无穷多个运动自由度，可在任意方向等效设置阻尼弹簧系统，为了使机理分析更清晰，屏蔽运动方程其余方向上的耦合运动，模型假设仅考虑纵向振动，将仪器舱支架等效为长度为l的杆，并假设连接点具有绝对刚度，系统等效结构图如图2所示。

图2 等效杆与阻尼弹簧振子组合系统

2 组合系统运动微分方程

杆的纵向受迫振动在结构动力学领域内已形成经典成熟理论，其运动微分方程为[6-7]

(1)

式中：杆长为l；材料密度为ρ；横截面积为A；材料弹性模量为E；纵向位移为u(x,t)；杆的纵向分布力为q(x,t)。

假设杆的两端固支，纵向分布力为常量F，初始条件均为0，可得到纵向杆的响应为

(2)

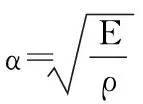
设阻尼弹簧振子安装于杆上的xi位置，则此时阻尼弹簧振子的运动微分方程为

(3)

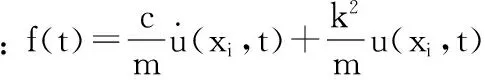
3 复模态分析

由于飞行器所承受的动态环境多呈现随机性，即对于等效系统输入的激振力并不能以确定性函数的形式表示，而是以随机过程描述，但根据力学随机振动理论，研究更为关心的是响应过程的数字特征[8]。

为了明确分析动态环境对惯导加速度计影响的机理，更应关注的物理量为组合系统中等效于本体的等效质量在杆的纵向产生的响应加速度，该响应直接由加速度计敏感并引入导航解算流程[9]。

引入状态变量

将式(3)改写为矩阵形式，可得

(4)

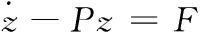
(5)

此时方程已解耦，由杜哈梅积分可以得到复模态响应z的平稳解

(6)

式中，hi(t)=epit，表示系统脉冲响应函数。

对于该组合系统其激励主要来自飞行过程中飞行器机体所产生的扰动，为了使激励-响应关系便于求解，不失一般性地假设受到的扰动为平稳随机激励[9]，其协方差函数为

(7)

此时复模态响应的协方差函数可表示为

(8)

由式(5)可得

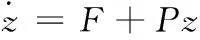
(9)

因此

(10)

进而根据复模态变换式并对其求导数，可以求得系统在纵向响应加速度的协方差函数为

(11)

当τ=0时，式(11)表示捷联惯导本体在受到平稳随机激励时，产生纵向加速度响应的方差。这一扰动加速度是动态环境中加速度计产生误差的根本原因之一。

4 影响机理分析

5 结论

1) 研究在仅考虑纵向振动的前提下，将飞行器仪器舱内的捷联惯导系统等效为连续杆与离散阻尼弹簧振子组成的组合系统。

2) 通过分析等效杆与阻尼弹簧振子混合系统微分方程，可以看到在外部出现随机激励的情况下，使捷联惯导加速度计敏感值变为围绕真实值分布的随机变量，这是动态环境造成加速度误差的根本原因之一。

3) 在一定假设条件下，利用复模态分析法对组合系统微分方程解耦，并推导了加速度响应的半解析表达式，对该模型的求解在已知纵向杆边界条件格林函数表达式的情况下，也可以利用格林函数法进行求解。

4) 仅考虑纵向振动的等效模型与设备的实际工况仍有较大差距，如果考虑支架的横向振动和扭转则需要将其考虑为欧拉梁和铁木辛柯梁，同时连续杆的响应表达式在使用时还需截断进行数值计算，所以模型并不适用于工程问题的直接求解，但模型用于分析动态环境对于捷联惯导误差的影响机理有很好的支撑作用。

[1] 谢燕.惯导支架结构的随机动力响应分析与参数优化[D].长沙:国防科技大学,2004.

[2] 付继波，马静，晁建军.弹性支撑惯导系统振动耦合问题研究[J].强度与环境,2005,32(2):46-51.

[3] MICHAEL A.BLENDER,HEIDI WILKIN.Flight dynamics of a hypersonic vehicle during inlet un-start[C]//16th AIAA/DLR/DGLR International Space Planes and Hypersonic System and Technologies Conference.AIAA-2009-7292.

[4] PAUL G.SAVAGE.Analytical modeling of sensor quantization in strapdown inertial navigation error equations[J].Journal of Guidance,Control and Dynamics,2002,25(5):833-842.

[5] 张希农，李智明.火箭仪器舱仪器安装板的振动控制试验研究[J].宇航学报,2002,23(1):76-78.

[6] 朱位秋.随机振动[M].北京：科学出版社,2016.

[7] 刘习军，贾启芬，张素侠.随机理论及工程应用[M].北京：机械工业出版社，2015.

[8] 方同.工程随机振动[M].北京：国防工业出版社，1995.

[9] 吴晓.长航时高精度捷联惯导系统误差抑制技术研究[D].哈尔滨:哈尔滨工程大学,2011.

[10]赵翔.多场耦合环境下梁横向振动的半解析解[D].成都:西南交通大学,2015.

(责任编辑 周江川)

Semi-Analytic Function of SINS Error Under Longitudinal Vibration Condition

YANG Qi1,3, SU Guohua2, LIU Qingbao1, LIU Xinxue3

(1.Sergeant College, the Rocket Force University of Engineering, Qingzhou 262500, China;2.The Rocket Force Equipment Research Institute, Beijing 100085, China;3.Primary Command College, the Rocket Force University of Engineering, Xi’an 710025, China)

Focusing on the SINS error between dynamic and static environment, the strap-down inertial system was equivalent to rod with damping spring vibrator system, which is considered under the hypothesis premise of exist only longitudinal vibration, and differential equation was decoupled with complex modal analysis, and the SINS error semi-analytic function under dynamic environment and the acceleration envelope range was deduced, and it finds out that the root cause of SINS error is the acceleration changed to a random variable around the true value under dynamic environment.

longitudinal vibration; strap-down inertial navigation; accelerometer; dynamic error

2017-04-22；

2017-05-20

杨其(1983—)，男，博士研究生，讲师，主要从事飞行器动力学与制导研究。

10.11809/scbgxb2017.08.004

format:YANG Qi, SU Guohua, LIU Qingbao, et al..Semi-Analytic Function of SINS Error Under Longitudinal Vibration Condition[J].Journal of Ordnance Equipment Engineering,2017(8):14-16.

V448

A

2096-2304(2017)08-0014-03

本文引用格式：杨其,苏国华,刘庆宝，等.纵向振动对捷联惯导误差影响半解析表达式研究[J].兵器装备工程学报，2017(8):14-16.