基于四分位法的含储能光伏电站可靠性置信区间计算方法

杨锡运 刘玉奇 李建林

(1.华北电力大学控制与计算机工程学院 北京 102206 2.中国电力科学研究院 北京 100192)

基于四分位法的含储能光伏电站可靠性置信区间计算方法

杨锡运1刘玉奇1李建林2

(1.华北电力大学控制与计算机工程学院 北京 102206 2.中国电力科学研究院 北京 100192)

为提高光伏电站接入系统能力，采用光储联合运行方式，研究加入储能前后光伏电站发电特性变化。为评估光储系统接入对电网可靠性的贡献，提出一种可靠性置信区间计算方法。首先对青海省格尔木某光伏电站历史数据做模糊C均值聚类，将其分为晴天、少云、多云、阴雨4种天气类型，利用四分位法对历史数据做统计分析，排除异常值。在此基础上提出一种光储系统功率带提取方法，搭建IEEE-RTS79可靠性测试系统，利用序贯蒙特卡罗法计算光储发电系统功率带对应的可靠性指标，从而得到含储能光伏电站可靠性置信区间。该可靠性区间计算结果为评价光储系统接入电网的可靠性贡献提供理论依据，对发电调度具有一定指导意义。

光伏 储能 四分位法 功率带 可靠性 置信区间

0 引言

光伏发电近年来发展迅速，在电力系统中的占比不断提高[1]。2016年一季度全国新增光伏装机容量714万kW，全国累计光伏发电装机容量达到5 031万kW，同比增加52%；一季度光伏发电量118亿kW·h，同比增加48%[2]。随着光伏电站大规模接入电网，光伏发电的出力不确定性对电力系统运行可靠性的影响日益增加。有效、准确地分析光伏电站接入系统后对发电可靠性影响及评估光伏电站置信容量为光伏发电的高效利用提供了理论基础，是光伏领域的热点研究问题[1]。

现有研究中，主要从以下几个方面分析光伏电站接入系统后对发电可靠性的影响：①以光伏发电建模为重点，建立准确的太阳辐照度模型和光伏电站出力模型：文献[3]在分析太阳辐照度波动模型的基础上，建立了考虑状态抽样转移的光伏电站多状态可靠性模型，有效提升了发电系统可靠性指标的计算准确性；文献[4]建立了考虑天气变化、设备故障等随机因素的光伏发电出力模型，并分析了不同模型计算光伏电站置信容量的差异；文献[5]建立了考虑光伏出力与电网负荷及光伏电站之间相关性的随机模型，并计算得到光伏出力的置信容量。②将光伏发电和储能系统相结合，利用储能系统的灵活充放电功能提高光伏电站的并网发电可靠性：文献[6]评估了储能容量配比与光伏装机容量大小对发电系统置信容量的影响；文献[7]研究了储能平抑光伏发电波动柔性并网的容量需求，提高光伏并网的可信容量；文献[8]基于粒子群优化方法分析了等可信容量下，以总投资成本最小为目标的风光储不同配比最优组合，提高并网可信度的同时兼顾其经济型。③以提高置信容量计算准确性为重点，研究并改进可靠性评估中的置信容量计算方法：文献[9]采用修正系数对等时间间隔采样方法进行修正，提升序贯蒙特卡罗法计算电力系统置信容量的执行效率；文献[10]改进了伪时序状态转移抽样这一可靠性评估方法，使其在储能接入系统的情况下快速准确地计算可靠性指标；文献[11]利用含衰老和竞争机制的粒子群算法ACM-PSO作为系统状态扫描和分类工具分析含光伏的发电系统可靠性问题。

上述研究充分考虑光伏电站的实际运行特性，从不同角度评估光伏发电置信容量及其在电力系统规划等方面的显著作用，但是对光伏电站本身的可靠性评价主要以计算光伏发电容量置信度为主，只能得到一个确定的指标用来评价光伏电站的可信度。因此，在现有研究基础上，本文提出光伏发电可信度区间的概念，不再局限于一个固定的可信度指标，着重分析其置信容量概率区间，这对评价光伏电站接入电网可靠性贡献程度、制订电站接入方案和确定电站日前出力计划等方面都具有一定价值。

综上，本文以青海格尔木某50 MW光伏电站为对象，应用数理统计中的四分位法排除电站功率数据异常值，重点分析电站在不同天气类型下的发电特性。相比基于假设检验的经典异常值识别方法(如基于正态分布的3σ法)，四分位法无需假定数据的分布形式，不受数据均值和标准差的影响，具有更高的耐抗性，更适用于光伏电站功率数据随机波动较高的数据处理应用场景。

根据文献[12]的研究结果可知，储能能够改善电网电能质量、平滑光伏出力波动、提高可再生能源发电接入能力。因此，本文研究在光伏电站中接入储能装置后的光储联合发电系统的发电特性。提出一种光储联合系统功率带提取方法，在对发电数据按天气特征进行模糊C均值聚类的基础上提取不同天气工况下的功率带。搭建IEEE-RTS79可靠性测试系统，应用序贯蒙特卡罗模拟法(Sequential Monte Carlo Methods)评估光储发电系统接入对电网可靠性指标的贡献。最后，以所提取的光储系统功率带为基础，提出一种含储能光伏电站的可靠性置信区间计算方法，为调度人员制定计划出力、电力调度提供理论依据。

1 光伏发电特性分析

光伏发电是一种新能源发电，受温度、辐照度等环境因素影响严重，具有随机性，造成发电功率的剧烈变化[13]。为评估光伏电站接入系统对电网可靠性的影响，需要对光伏电站的发电特性有深入了解。

1.1 四分位法

四分位法是统计学中分析数据集分布特征的重要方法，原理如图1所示，是指将数据集中的全部数据按大小顺序依次排列并分为四等份，处于分割点位置的三个数值Q1、Q2、Q3就是四分位数。计算流程如图2所示。

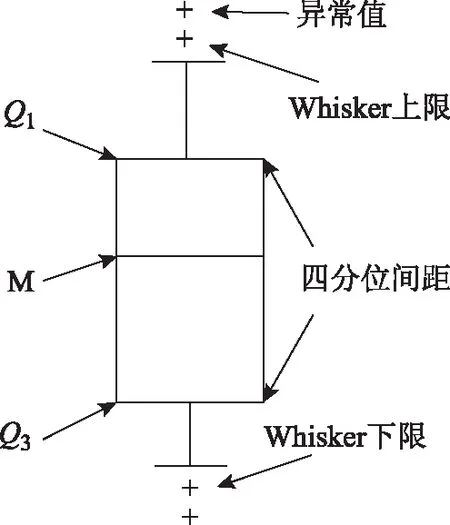
图1 四分位法示意图Fig.1 Schematic diagram of the quartile method

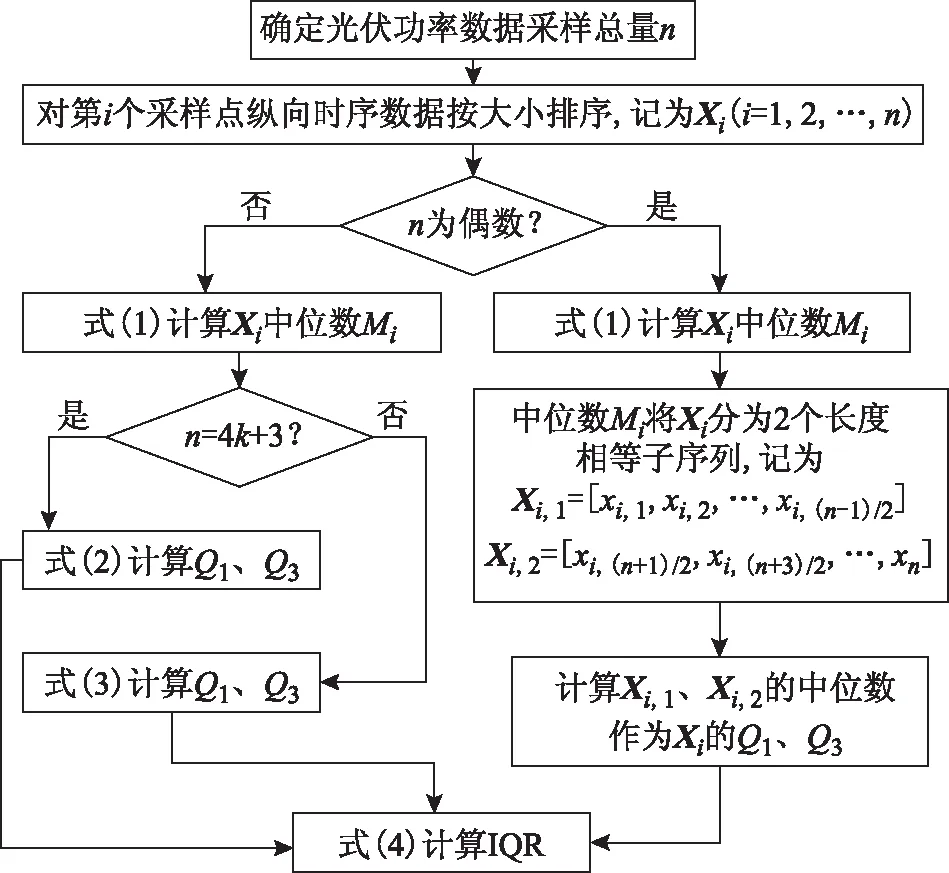
图2 四分位法计算流程Fig.2 Calculation process of the quartile method

计算方法如下[14]：

记第i个采样点光伏电站功率纵向时序矢量为Xi=[xi，1，xi，2，…，xi，n]，其中i=1，2，…，n，xi，1≤xi，2≤…≤xi，n-1≤xi，n。第二分位数Mi表示纵向时序矢量Xi的中位数，计算公式为

(1)

式中，n为光伏电站数据采样总量，d。

第一、三分位数表示Xi中分隔前、后25%数据点的位置所表示的数值。采样总量n不同时，计算公式略有差异：

1)n为偶数时，Mi将Xi分为长度相同的两个子序列，记为Xi，1=[xi，1，xi，2，…，xi，(n-1)/2]和Xi，2=[xi，(n+1)/2，xi，(n+3)/2，…，xn]，Q1，i、Q3，i分别表示子序列Xi，1和Xi，2的中位数。

2)n=4k+3(k=0，1，2，…)时，计算公式为

(2)

3)n=4k+1(k=0，1，2，…)时，计算公式为

(3)

如图1所示，Xi的四分位间距表示大小处于Xi中间50%的xi(i=1，2，…，n)的集合，四分位间距框的大小整体反应光伏功率数据的集中程度，是光伏电站有功出力波动的体现。根据式(2)、式(3)的计算结果，可以得到Xi的四分位间距IQRi为

IQRi=Q3,i-Q1,i

(4)

1.2 光伏输出功率异常点处理

光伏发电过程可能受到设备故障[4]、天气突变[15]等因素的影响，使得少部分数据点表现异常，称之为异常点，如图1中“+”所示。异常点在光伏电站输出功率分析中会影响对电站基本发电特性的判断，为准确研究光伏电站正常工作条件下的发电特性，需要排除异常数据点的影响。

四分位法中，用Whisker上限Wu，i、下限Wd，i来排除数据中的异常值，计算公式为

(5)

根据式(5)的计算结果，定义纵向时序矢量Xi中处于Wu，i和Wd，i之间的功率点为Xi正常值，之外的数据点为Xi异常值。

2 储能系统模型

为减小光伏发电随机波动对电能质量及电网接入能力的影响，储能技术受到广泛应用[16，17]。实际光伏发电数据由于其随机波动特性使部分数据特性呈高频状态，这是由于光伏电站工作状态受天气因素影响较大，当存在严重云遮时会改变电池板接受太阳辐射程度，使其功率发生波动。为减小光伏电站输出功率波动，需要对光伏电站输出功率进行平滑处理，消除日功率曲线中毛刺现象，降低光伏功率波动率，提高光伏电站并网能力。

2.1 储能系统控制策略

利用储能系统平抑光伏波动是优化光伏电站功率输出、改善光伏并网运行性能的重要手段。储能并网标准参照国家电网公司《光伏电站接入电网技术规定》，即光伏电站分钟变化率不超过装机容量的10%。本文采用传统低通滤波环节对光伏电站输出功率进行平滑处理，按文献[7]制定储能系统控制策略为

Pall,k=αPall,k-1+(1-α)Ppv,k
α=τ/(τ+Δt)
Pbat,k=Pall,k-Ppv,k

(6)

式中，Pall，k为k时刻平抑后的输出功率；Ppv，k为k时刻光伏电站输出功率；Pbat，k为k时刻储能系统输出功率；Δt为采样时间间隔；τ为低通滤波器时间常数。

根据式(6)，k时刻光伏电站输出功率Ppv，k经过一阶低通滤波环节平滑后输出功率Pall，k，将Pall，k作为光伏电站并网参考值。平滑前功率Ppv，k和平滑后功率Pall，k的差值Pbat，k作为储能系统控制信号。当Pbat，k>0时，光伏电站实际输出功率小于并网参考值，储能放电；Pbat，k<0时，光伏电站实际输出功率大于并网参考值，储能充电。

2.2 储能系统约束条件

储能系统需满足以下约束条件[18]：

1)储能容量约束。为避免储能电池过度充放电，延长电池使用寿命，需加入储能容量状态约束，限制其充放电深度。

0.2≤SOCt≤0.8

(7)

2)充放电功率约束。

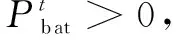
(8)

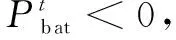
(9)

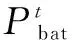
为满足以上约束条件，需规定电池实时荷电状态SOCt的取值上、下界为

(10)

计算公式为

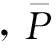
(11)

3 可靠性区间计算方法

3.1 序贯蒙特卡罗方法

蒙特卡罗法(Monte Carlo)是一种以概率统计为理论基础的数值计算方法，被广泛用于电力系统风险评估中[19]。序贯蒙特卡罗法是在非序贯蒙特卡罗法的基础上考虑系统在时间上的连续性，对所有元件的工作状态持续时间抽样，构成系统的时序状态，并做可靠性分析[20]。相比于非序贯蒙特卡罗法，其优势在于具有明确的物理意义，算法复杂性低、缺点是收敛速度慢，适用于提前性的电网可靠性规划。

电力系统序贯蒙特卡洛仿真流程如图3所示。

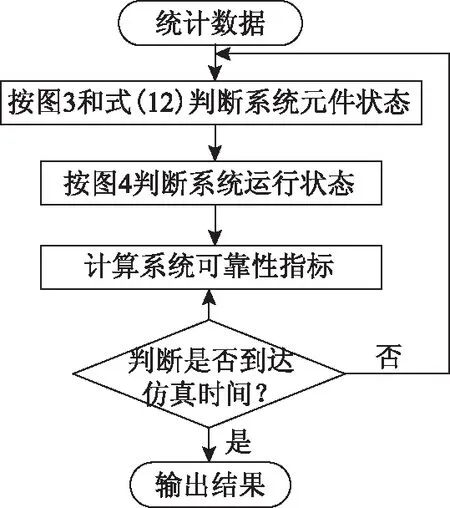
图3 序贯蒙特卡洛仿真流程Fig.3 Flow chart of sequential Monte Carlo simulation

其中系统元件状态由图4所示的两状态模型确定，元件的下次故障预计发生时间TTTF和故障预计修复时间TTTR计算公式为[21]

(12)

式中，TMTTF、TMTTR分别为平均无故障运行时间和平均修复时间；R1、R2为(0，1)之间均匀分布的随机数。

图4 状态元件的状态转移Fig.4 State transition of the elements

假定系统由k个元件组成，各元件运行状态由式(12)确定，则t时刻系统运行状态St由各元件运行状态xkt共同确定，如图5所示，图中“1”代表元件运行，“0”代表元件故障。

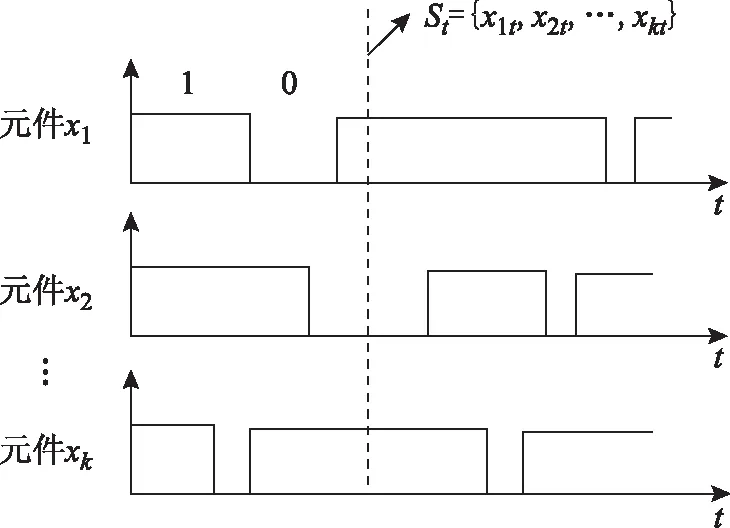
图5 系统运行状态判定Fig.5 System operation state determination

3.2 光储系统功率带提取方法

光储系统的功率带在不同天气时具有清晰的功率带现象，但是其幅值、带宽均不相同，且差异明显。因此，本文将光储系统出力按天气分为4种典型工况，分别提取其功率带。

光储系统功率带提取步骤如下：

1)统计光伏电站历史输出功率数据，将电站出力工况按天气分为晴天、少云、多云、阴雨4种类型。

2)应用FCM方法对统计数据做聚类分析，聚类特征选取太阳辐照度波动量VI、最大辐照比例Kr、环境温度T。

3)在光伏电站中接入储能环节，对光伏电站的输出功率进行平滑处理，降低输出功率的波动率，使电站出力平稳。

4)采用四分位法，计算光储系统发电数据的四分位数Q1、Q2、Q3，Whisker上、下限Wu、Wd。

5)根据Wu、Wd值，排除电站输出功率数据中的异常点。

6)寻找数据有效点中的每一采样时刻的历史最大、最小值，以全部时刻的最大、最小值相结合创建电站的输出功率上、下包络线，从而得到光储系统功率带，即包络线所包围部分区域。

3.3 可靠性区间计算步骤

1)搭建可靠性测试系统IEEE-RTS79，具体参数详见文献[22]，可靠性指标[23]选择失负荷概率(Loss of Load Probability，LOLP)，表示系统中出现停电事件的概率，无量纲；电力不足期望(Expected Power Not Supply，EPNS)，量纲为兆瓦(MW)；电力不足频率(Loss of Load Frequency，LOLF)表示单位时间内系统出现切负荷故障次数，量纲为次/年。计算公式为

(13)

式中，FLOLP(Xi)和FEPNS(Xi)分别为与LOLP、EPNS对应的试验函数，FLOLP(Xi)由式(14)计算得到，FEPNS(Xi)表示系统在随机状态Xi下总的有功负荷切除功率；CL为仿真时间内切负荷数；T为系统总仿真时间；ti为系统状态Xi的持续时间。

(14)

2)接入光储发电系统，接入方案参考文献[24]的分布式接入方法。

3)根据光储功率带提取结果，假设光储系统输出功率恒为功率带的上限或下限，仿真得到可靠性结果，从而得到该光伏电站在此接入方式下的可靠性区间。

4 算例分析

本文选取青海省格尔木50MW光伏电站，数据采样总量为365天，采样间隔为0.25h，每天96个数据点，数据采用标幺值。对每一采样时刻纵向时序中全部365个数据点做四分位法统计分析，共96组数据。根据四分位法，绘制如图6所示光伏电站输出功率箱须图。观察图6可得每个采样点光伏电站输出功率的分布区间，包括其最大、最小值和中位数位置等。

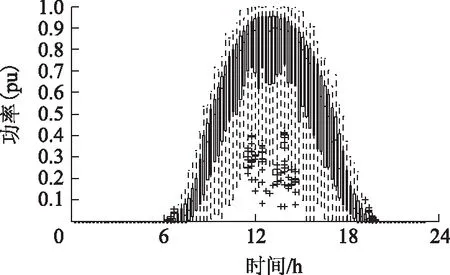
图6 光伏电站输出功率箱须图Fig.6 Box-and-whiskers plot for output power of photovoltaic power station

4.1 光伏发电天气特性

天气变化是影响光伏电站发电能力的重要因素，为分析天气因素对光伏发电特性影响，采用文献[25]中模糊C均值聚类法(Fuzzy-C-Means，FCM)对光伏电站历史功率数据按天气不同做聚类分析。将天气分为晴天、少云、多云、阴雨4种基本类型，聚类特征采取太阳辐照度波动量VI、最大辐照比例Kr、环境温度T。

应用四分位法对聚类结果中不同天气下的光伏发电日功率曲线做统计分析，得到结果如图7所示。

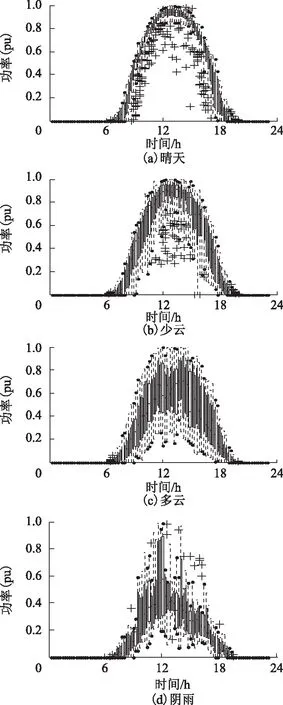
图7 光伏电站日有功功率箱须图Fig.7 Box-and-whiskers plot for daily active power of photovoltaic power station

从图7a、图7b中能够看出，4种不同天气类型下光伏电站有功出力差异明显。晴天和少云天气的中位数位置、四分位间距框的位置与高度基本相同，说明这两种类型天气条件下光伏电站有功出力水平差异不明显。但从Whisker上限和Whisker下限来看，晴天时四分位间距框更窄，说明晴天时电站有功出力的波动较小。图中“+”点表示异常数据点，由1.2节方法确定。由图7可见，随着天气情况由晴到多云、阴雨变化，数据中异常点数量减少。这是由于晴天时太阳辐照度几乎不受云遮影响，导致存在微云时较小的太阳辐照波动也会在四分位法分析中被判定为异常点；多云天气时太阳辐射受云遮影响严重，异常点个数减少。

4.2 光储系统发电特性分析

根据光伏电站实际运行情况，储能系统采用15 MW×1.2 h=18 MW·h的磷酸铁锂电池，充放电效率nc=nd=90%。光伏电站输出功率经储能装置平滑后波动率降低、异常点减少，说明每个采样时刻功率值收紧在一个更小的范围内，如图8所示。相比于图6所示光伏电站输出功率箱须图，图8中光储系统输出功率的数据分布离散性明显减小，其中多云工况时尤为明显。这是由于在4种天气类型中，多云天气受到云遮影响更严重，波动率更高。晴天工况下，光储系统的异常值减少，这是由于储能装置的平滑作用消除了晴天工况的偶尔云遮所导致的输出功率下降，从图8a可知输出功率曲线的重合程度更高。

根据3.2节中功率带提取方法，图9给出计算得

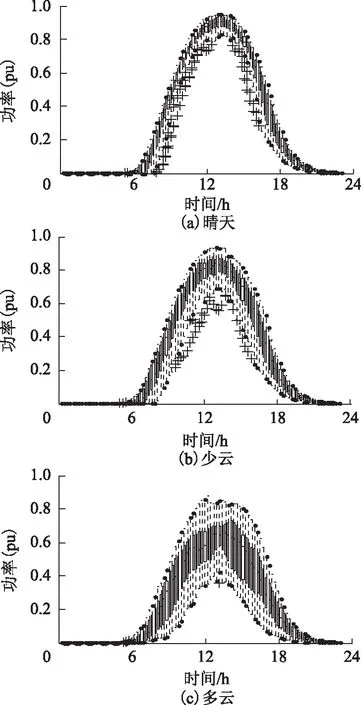
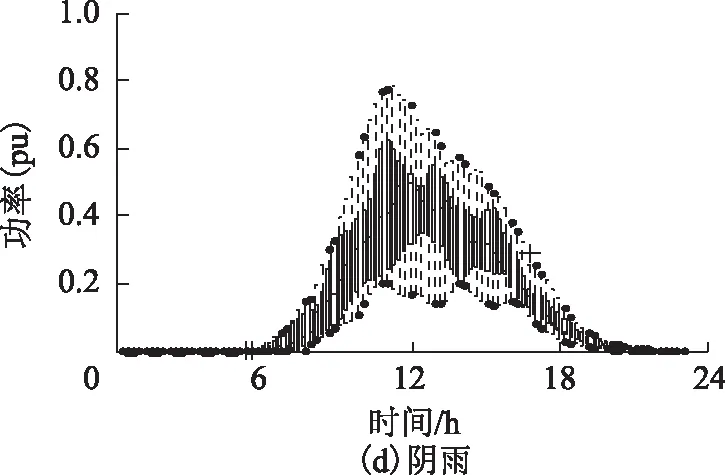
图8 光储系统日有功功率箱须图Fig.8 Box-and-whiskers plot for daily active power of PV and ESS generation system

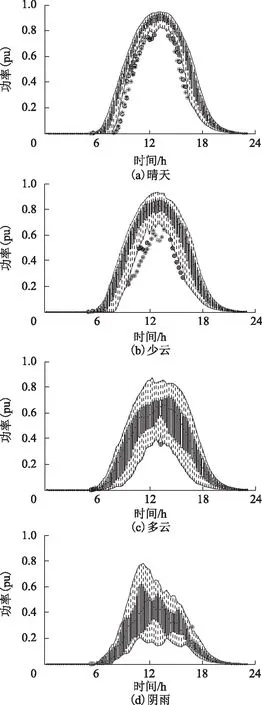
图9 光伏电站功率带Fig.9 Power bands of photovoltaic power station

到的4种不同天气类型工况下光储系统功率带。图中“⊕”为被排除的异常点。

观察图9可知，晴天和少云天气的功率带较窄，分布较为集中；多云和阴雨天气由于受云遮影响严重，电池板接受太阳辐照波动较大，使得功率带较宽。

4.3 可靠性区间计算结果

以晴天条件下LOLP指标为例，绘制如图10所示含光储系统LOLP置信区间曲线，图中可明显看出LOLP指标在晴天条件下的变化区间。根据表1中结果可知，不同类型天气条件下含光储系统的LOLP、EPNS、LOLF可靠性指标差异明显，验证了文献[4]中天气变化对光伏发电系统可靠性影响较大的结论。表1中Max和Min分别对应光储系统功率带的下限、上限计算得到的可靠性指标，光储系统出力越高，可靠性指标越低。

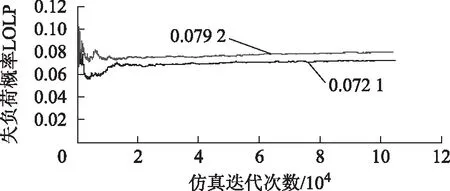
图10 晴天条件LOLP指标变化区间收敛曲线Fig.10 Convergence curve of LOLP index in sunny days

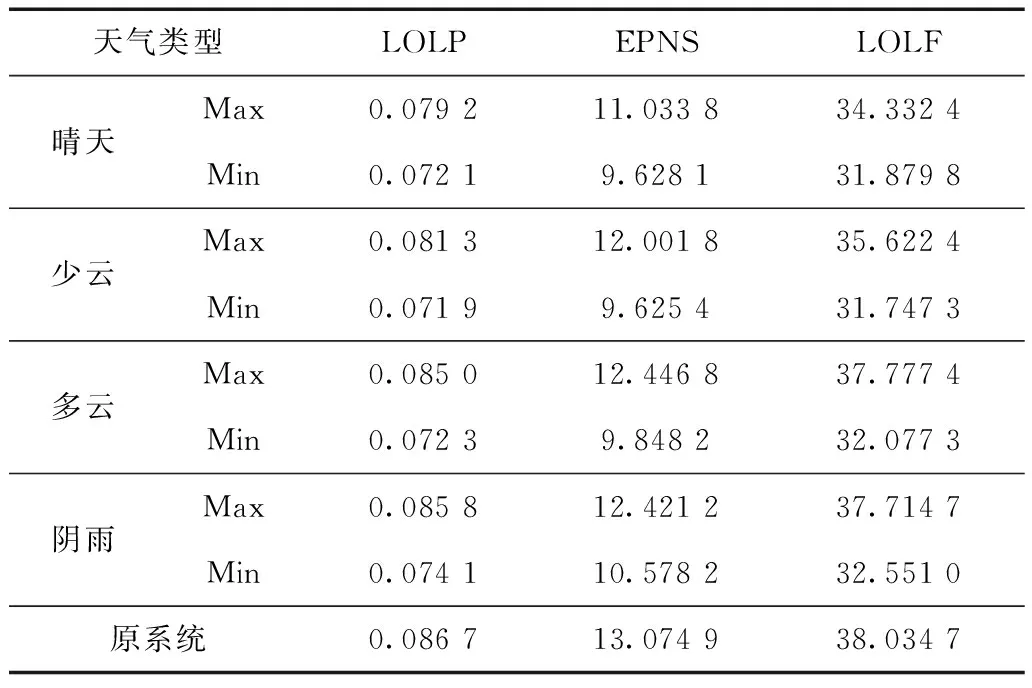
天气类型LOLPEPNSLOLF晴天Max0.079211.033834.3324Min0.07219.628131.8798少云Max0.081312.001835.6224Min0.07199.625431.7473多云Max0.085012.446837.7774Min0.07239.848232.0773阴雨Max0.085812.421237.7147Min0.074110.578232.5510原系统0.086713.074938.0347

表1中的计算结果表征不同天气时含光储发电系统的可靠性区间，在提取光储系统功率带的基础上计算得到。例如，根据本文计算结果可知，多云天气下指标LOLP取值区间为0.072 3～0.085 0，若次日天气为多云，可估计次日可靠性指标LOLP值在上述区间内。可靠性区间计算能够根据光储系统的历史发电数据评估该系统接入电网后的可靠性贡献，对天气变化时的调整计划出力、指导电力调度具有重要意义。

5 结论

为提高光伏电站接入系统能力，评估光伏电站接入系统对电网可靠性指标贡献，本文研究了以下几方面内容：

1)首先采用四分位法对青海省格尔木某光伏电站历史发电数据做统计分析。为考虑天气变化因素，应用模糊C均值聚类方法将光伏电站分为晴天、少云、多云、阴雨4种天气工况。

2)在光伏电站中加入储能装置，利用其平抑随机波动作用提高光伏电站接入系统能力，并分析光伏电站接入储能前后的发电特性变化。

3)利用四分位法排除光储系统发电数据中的异常点，并提出一种光储联合系统功率带提取方法，计算得到光储发电系统4种天气工况下的功率带。

4)利用序贯蒙特卡罗方法，计算含储能光伏电站可靠性置信区间。

运用本文提出的方法计算得到光储电站可靠性置信区间，该计算结果适用于评估光储发电系统的接入电网能力，为制订光伏计划出力及电力调度提供理论依据。

[1] 丁明，王伟胜，王秀丽，等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报，2014，34(1)：1-14. Ding Ming，Wang Weisheng，Wang Xiuli，et al.A review on the effect of large-scale generation on power system[J].Proceedings of the CSEE，2014，34(1)：1-14.

[2] 2016年第一季度光伏发电建设和运行信息简况-国家能源局[Z].http：//www.nea.gov.cn/2016-04/22/c_135303838.htm.2016.

[3] 王敏，宗炫君，袁越，等.含光伏电站的发电系统可靠性分析[J].中国电机工程学报，2013，33(34)：42-49. Wang Min，Zong Xuanjun，Yuan Yue，et al.Reliability analisys of generation systems with photovoltaic stations[J].Proceedings of the CSEE，2013，33(34)：42-49.

[4] 王秀丽，武泽辰，曲翀.光伏发电系统可靠性分析及其置信容量计算[J].中国电机工程学报，2014，34(1)：15-21. Wang Xiuli，Wu Zechen，Qu Chong.Reliability and capacity value evaluation of photovoltaic generation systems[J].Proceedings of the CSEE，2014，34(1)：15-21.

[5] 梁双，胡学浩，张东霞，等.基于随机模型的光伏发电置信容量评估方法[J].电力系统自动化，2012，36(13)：32-37. Liang Shuang，Hu Xuhao，Zhang Dongxia，et al.Probabilistic models based evaluation method for capacity credit of photovoltaic generation[J].Automation of Electric Power Systems，2012，36(13)：32-37.

[6] 何俊，邓长虹，徐秋实，等.风光储联合发电系统的可信容量及互补效益评估[J].电网技术，2013，37(11)：3030-3036. He Jun，Deng Changhong，Xu Qiushi，et al.Assessment on capacity credit and complementary benedit of power generation system integrate with wind farm，energy storage system and photovoltaic system[J].Power System Technology，2013，37(11)：3030-3036.

[7] 张卫东，刘祖明，申兰先.利用储能平抑波动的光伏柔性并网研究[J].电力自动化设备，2013，33(5)：106-111. Zhang Weidong，Liu Zuming，Shen Lanxian.Flexible grid-connection of photovoltaic power generation system with energy storages system for fluctuation smoothing[J].Electric Power Automation Equipment，2013，33(5)：106-111.

[8] 何俊，邓长虹，徐秋实，等.基于等可信容量的风光储电源优化配置方法[J].电网技术，2013，37(12)：3317-3324. He Jun，Deng Changhong，Xu Qiushi，et，al.Optimal configuration of distributed generation system containing wind PV battery power sources based on equivalent credible capacity theory[J].Power System Technology，2013，37(12)：3317-3324.

[9] 暴英凯，王越，唐俊熙，等.序贯蒙特卡洛方法在电力系统可靠性评估中的应用差异分析[J].电网技术，2014，38(5)：1189-1195. Bao Yingkai，Wang Yue，Tang Junxi，et al.Analysis on differences of applying Sequential Monte Carlo methods in power grid reliability assessmeng[J].Power System Technology，2014，38(5)：1189-1195.

[10]程林，常垚，刘满君，等.基于伪时序状态转移抽样法评估含储能电力系统可靠性[J].电力系统自动化，2014，38(7)：53-59. Cheng Lin，Chang Yao，Liu Manjun，et al.Reliability evaluation of energy storage integrated power system based on Pseudo-sequential state transition sampling algorithm[J].Automation of Electric Power Systems，2014，38(7)：53-59.

[11]余志强，王淳，胡奕涛，等.并网光伏发电置信容量评估[J].电力系统保护与控制，2016，44(7)：122-127. Yu Zhiqiang，Wang Chun，Hu Yitao，et al.Capacity credit evaluation of grid-connected photovoltaic generation[J].Power System Protection and Control，2016，44(7)：122-127.

[12]李建林，田立亭，李春来.储能联合可再生能源分布式并网发电关键技术[J].电气应用，2015，34(9)：28-33. Li Jianlin，Tian Liting，Li Chunlai.Key technology of distributed grid connected power generation with energy storage and renewable energy[J].Electrotechnical Application，2015，34(9)：28-33.

[13]沈鑫，曹敏.分布式电源并网对于配电网的影响研究[J].电工技术学报，2015，30(增刊1)：346-351. Shen Xin，Cao Min.Research on the influence of distributed power grid for distribution network[J].Transactions of China Electrotechnical Society，2015，30(S1)：346-351.

[14]赵永宁，叶林，朱倩雯.风电场弃风异常数据簇的特征及处理方法[J].电力系统自动化，2014，38(21)：39-46. Zhao Yongning，Ye Lin，Zhu Qianwen.Characteristics and processing method of abnormal data clusters caused by wind curtailments in wind farms[J].Automation of Electric Power Systems，2014，38(21)：39-46.

[15]方鑫，郭强，张东霞，等.考虑天气不确定性的光伏电站置信容量评估[J].电力系统自动化，2012，36(10)：27-32. Fang Xin，Guo Qiang，Zhang Dongxia，et al.Capacity credit evaluation of grid-connected photovoltaic generation considering weather uncertainty[J].Automation of Electric Power Systems，2012，36(10)：27-32.

[16]刘皓明，陆丹，杨波，等.可平抑高渗透分布式光伏发电功率波动的储能电站调度策略[J].高电压技术，2015，41(10)：3213-3223. Liu Haoming，Lu Dan，Yang Bo，et al.Sispatch strategy of energy storage station to smooth power fluctuations of high penetration photovoltaic generation[J].High Voltage Engineering，2015，41(10)：3213-3223.

[17]李滨，陈姝，梁水莹.一种平抑光伏系统输出波动的储能容量优化方法[J].电力系统保护与控制，2014，42(22)：45-50. Li Bin，Chen Shu，Liang Shuiying.Acapacity optimization of energy storagy system for output smoothing of photovoltaic station[J].Power System Protection and Control，2014，42(22)：45-50.

[18]Fossati J P，Galarza A，Martín-Villate A，et al.A method for optimal sizing energy storage systems for microgrids[J].Renewable Energy，2015，77：539-549.

[19]张建华，王昕伟，蒋程，等.基于蒙特卡罗方法的风电场有功出力的概率性评估[J].电力系统保护与控制，2014，42(3)：82-87. Zhang Jianhua，Wang Xinwei，Jiang Cheng，et al.Probabilistic assessment of wind farm active power based on Monte-Carlo simulation[J].Power System Protection and Control，2014，42(3)：82-87.

[20]王杨，谢开贵，胡博，等.基于时序模拟的离网型微网可靠性分析[J].电工技术学报，2016，31(6)：206-211. Wang Yang，Xie Kaigui，Hu Bo，et al.Reliability analysis of islanded microgrid based on sequential simulation[J].Transactions of China Electrotechnical Society，2016，31(6)：206-211.

[21]别朝红，李更丰，谢海鹏.计及负荷与储能装置协调优化的微网可靠性评估[J].电工技术学报，2014，29(2)：64-73. Bie Chaohong，Li Gengfeng，Xie Haipeng.Reliability evaluation of microgrids considering coordinative optimization of loads and storage devices[J].Transactions of China Electrotechnical Society，2014，29(2)：64-73.

[22]Subcommittee P M.IEEE reliability test system[J].IEEE Transactions on Power Apparatus & Systems，1979，PAS-98(6)：2047-2054.

[23]宋晓通.基于蒙特卡罗方法的电力系统可靠性评估[D].济南：山东大学，2008.

[24]张硕.计及风电场容量可信度的电力系统可靠性研究[D].北京：华北电力大学，2010.

[25]Mosadeghy M，Yan Ruifeng，Saha T K.Impact of PV penetration level on the capacity value of South Australian wind farms[J].Renewable Energy，2016，85：1135-1142.

(编辑 赫蕾)

Reliability Confidence Interval Calculation Method for Photovoltaic Power Station with Energy Storage Based on Quartile Method

YangXiyun1LiuYuqi1LiJianlin2

(1.School of Control and Computer Engineering North China Electric Power University Beijing 102206 China 2.China Electrical Power Research Institute Beijing 100192 China)

In order to improve the capacity of photovoltaic station access the power generation system，a combined operation mode integrated with photovoltaic(PV)system and energy storage system(ESS)is established to study the characteristics of photovoltaic power station before and after adding energy storage system.A reliability confidence interval calculation method is proposed in order to evaluate the contribution to the reliability of power grid which has PV and ESS.Firstly，Fuzzy-C-Means clustering is done to the historical data of a photovoltaic power station in Golmud，Qinghai province，dividing the historical data into four kinds of weather types，sunny，cloudy，partly cloudy，rainy.Analyzing the historical data and eliminating the outliers by using the Quartile Method.On this basis，an extraction method of power band for PV and ESS generation system is proposed in this paper.Building the IEEE-RTS79 reliability test system and using sequential Monte Carlo method to calculate the reliability index of the power band of PV and ESS generation system，resulting in containing the reliability confidence interval of this system.The results of the reliability interval calculation provides a theoretical basis for evaluating the reliability of the PV and ESS generation system access to the power grid，and it has great guiding significance for the power generation scheduling.

Photovoltaic，energy storage，quartile method，power band，reliability，confidence interval

国家自然科学基金项目(51677067)、中央高校基本科研业务费专项资金项目(2015MS32)、北京市自然科学基金项目(4132061)和国家电网公司项目(DG71-15-039)资助。

2016-05-10 改稿日期2016-09-14

10.19595/j.cnki.1000-6753.tces.160650

TM743

杨锡运 女，1973年生，教授，研究方向为新能源发电技术等。

E-mail：yangxiyun916@sohu.com

刘玉奇 男，1991年生，硕士研究生，研究方向为新能源发电技术等。

E-mail：liu_yuqi0926@163.com(通信作者)