基于梯度正则化联合重构河流水质模型多项参数

邢利英, 孙三祥，张国珍

(1.兰州交通大学环境与市政工程学院，甘肃 兰州 730070；2.南阳师范学院土木与建筑工程学院，河南 南阳 473061)

基于梯度正则化联合重构河流水质模型多项参数

邢利英1,2, 孙三祥1，张国珍1

(1.兰州交通大学环境与市政工程学院，甘肃 兰州 730070；2.南阳师范学院土木与建筑工程学院，河南 南阳 473061)

为识别河流水质模型参数，首先采用Crank-Nicolson有限差分格式离散控制方程，其次通过附加终端观测值，设计梯度正则化算法重构河流水质模型的多项参数。结果表明，不管是顺直河流的常系数模型，还是天然的线性相关或者线性无关的变系数模型，梯度正则化方法均能快速有效识别模型参数；初值和测量误差对参数重构影响较小，充分证明梯度正则化算法是一种有效稳定地反演河流水质模型参数的方法。

水质模型；模型参数；参数重构；Crank-Nicolson；梯度正则化

随着社会经济的快速发展，河流污染日趋严重。及时查找河流污染的具体原因，建立河流的水质模型，掌握河流污染物浓度的时空变化，对于水环境预测、水污染控制治理和生态修复等诸多方面有重要的意义。其中水质模型参数估计是建立水质模型的一个非常重要环节，而水质模型应用的成败很大程度上取决于参数估计是否正确[1-5]。通常模型参数可以通过模型试验或经验值法确定，然而模型试验往往工作量较大、效率较低，而经验值法很难保证其普适性。目前较为常用的方法是参数调试，实际上是根据实测的数据来调试参数，使得预测结果与实测数据吻合，即是基于初始边界条件识别控制方程的参数[6-7]。

参数识别对于实际测量中污染源的位置、污染物排放时间、污染物扩散系数的测量等具有一定的理论参考和实际应用价值。目前在河流污染水质模型中，参数反演已经取得一定的成功。参数反演方法主要有随机性优化算法和确定性算法[8]，随机性优化算法主要包括遗传算法、基于马尔科夫链的贝叶斯法(Bayesian-Markov ChainMonte Carlo，B-MCMC)、模拟退火法、单纯形法等；确定性算法有共轭梯度法、时空全域函数配点法(Globalspace-time Multi-quadric，MQ)、Landweber迭代法、Tikhonov正则化法等。朱嵩等[9]提出了有限体积法结合混合遗传算法的参数识别算法。薛红琴等[10]采用有限差分法结合单纯形法的参数识别算法来反演天然河流的水质参数。江思珉等[11]分别利用单纯形模拟退火法和Hooke-Jeeves吸引扩散粒子群混合算法求解地下水污染源反演的模拟—优化模型。邢利英等[12]应用改进的共轭梯度法识别地下水污染源。Li等[13-14]提出基于时空全域MQ函数配点法构造反演模型，求解地下水污染源识别初值反问题。李功胜等[15]成功地应用一种最佳迭代正则化算法反演污染源项，数值结果表明在测量数据存在干扰时，这种算法仍可以精确稳定地反演源项。范小平等[16]结合最佳摄动思想的遗传算法确定了淄博沣水南部地区的地下水硫酸污染源强度。

上述研究中，参数识别方法均能有效地识别河流水质模型的某项参数，而对于多个参数的联合识别研究较少。刘进庆等[17]应用梯度正则化方法重构地下水污染强度，该算法精度高，收敛速度快，稳定性好。本文应用具有二阶精度的Crank-Nicolson格式离散控制方程，采用梯度正则化方法进行河流污染水质模型的参数识别，分别联合重构常系数和变系数河流水质模型中的多项参数，并且考虑参数之间的耦合和非耦合情况。

1 Crank-Nicolson格式对控制方程的离散化

1.1 河流污染的控制方程及反问题

假定河流中污染物按一级动力学衰减，河流一维水质模型控制方程为

(1)

式中：Q为研究区域，Q=[0,L]×[0,T]；ρ(x,t)为测点(x,t)处的污染物浓度；u为河流的平均流速；Ex为x方向扩散系数；K为综合降解系数;f(t)为边值条件。

如果上述方程中的各参数u、Ex、K、f(t)均已知，方程(1)则构成了一个正问题，可以通过模型试验和数值模拟方法预测河流下游污染物浓度ρ(x,t)，从而可以推断河流的污染情况。然而大多数情况下，u、Ex、K往往不能准确地测得，因此上述问题也就转化为参数识别反问题，即如何确定一组〈ρ(x,t),u,K,Ex〉满足方程(1)。求解上述反问题，需要附加终端观测值

ρT(x)=φ(x)

(2)

式中：ρT(x)为T时刻的终端观测值；φ(x)为终端观测函数。

由此，式(1)和(2)构成一个关于河流水质模型参数识别问题，可以应用迭代的方法求解。

1.2 Crank-Nicolson离散控制方程

xi=iΔxi=0,1,…,M

(3)

tn=nΔtn=0,1,…,N

(4)

Crank-Nicolson格式是一种加权隐式格式，其截断误差为O(Δx2+Δt2)，即具有二阶精度，被广泛地应用在偏微分方程的求解中[1,19]。上述河流污染的控制方程建立Crank-Nicolson差分格式为

(5)

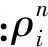
经过简化，式(5)可转化为

(6)

方程(6)的矩阵表达式为

Gρn+1+Z=Bρn+Qn=1,2,…,N

(7)

其中

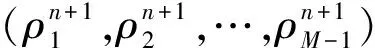
(8)

(9)

(10)

(11)

G和B是典型的三对角矩阵

(12)

(13)

对于所有的内部节点都可列出方程(7), 利用初边界条件可得到一个主对角元占优的三对角方程组，可以应用追赶法求解上述方程组。

1.3 Crank-Nicolson差分方程的稳定性

稳定性是判断反问题是否适定的条件之一，本文应用极值原理证明Crank-Nicolson差分格式的稳定性[20-21]。方程(6)可变形为

(14)

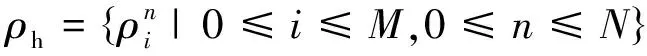
(2-2s+2KΔt)‖ρn‖∞+(r+s)‖ρn‖∞

0≤i≤M-1,0≤n≤N-1

(15)

(16)

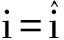
(17)

当0≤i≤M-1则有

‖ρn+1‖∞≤(1+KΔt)‖ρn‖∞

(18)

式(16)对于任意的0≤i≤M得

‖ρn‖∞≤(1+KΔt)‖f‖∞

(19)

(20)

(21)

基于上述稳定性的证明，同理有

‖εn‖∞≤(1+KΔt)‖Ψ‖∞0≤i≤M

(22)

2 梯度正则化法

a. 建立迭代过程：

Dn+1(x)=Dn(x)+δDn(x)

(23)

其中，摄动量δDn(x)是由下列非线性最优化问题来确定：

αE[δDn]

(24)

式中：α为正则化参数；E[δDn]为[δDn]的稳定化泛函；A为导数矩阵；Jα为非线性泛函。

b. 对上述最优化问题进行离散，采用线性化方法求得δDn(x)的数值解，即求解非线性化最优化问题的局部极小值。

根据以上的算法，梯度正则化法的具体迭代步骤[3,15]如下：

步骤1：确定正则化参数，步长及初始值，(x,t)的离散点以及求解精度EPS；

步骤2：根据已知参数求解方程(1)，得到ρ(xi,T,Wj)；

步骤3：设在计算区间有M个离散点xm(m=1,2,…,M)，由

步骤4：计算δWi=(ATA+a)-1AT(V-D), 其中V为附加数据；

3 常系数模型的多参数重构

选取3个典型的数值算例验证梯度正则化算法的有效性和普适性，采用孪生实验，即设定准确参数，利用同一模型生成观测数据，设参数未知进行识别试验。

3.1 正问题的求解

设一均匀河段长30 km，计算时间取1 h，离散的空间步长取1.5 km，时间步长取1/15 h，污染物的质量浓度边界值ρ0取1 mg/L，河流的平均流速u取5 km/h，弥散系数Ex取2 km2/h，污染物的一级降解速率K取0.015 h-1，算例数据引自文献[9]。此种离散情况下，Peclet数为3.75，属于非对流占优问题，对流项采用中心加权差分格式是比较精确的，数值弥散与振荡不明显。采用Crank-Nicolson的有限差分格式求解的计算结果见图1，可以看出，计算结果较为光滑，这是由于Crank-Nicolson是二阶精度，截断误差为O(Δx2+Δt2)。

3.2 多参数重构

常系数模型参数估计结果见表1，其中求解精度EPS取10-3，初值相同，真值为u=5 km/h，Ex=2 km2/h，K=0.015 h-1，与相关文献的共轭梯度法[12]和混合遗传算法[9]的反演结果相比，发现梯度正则化方法比其他2种方法更快、更有效地重构河流污染的模型参数，因此下面的模型参数识别中，均采用梯度正则化方法重构模型参数。

表1 几种方法常系数模型参数估计结果

3.3 初值对参数重构的影响

选取不同初值，应用梯度正则化方法重构参数的结果见表2，其中x*为精确值，从表中数据可以看出，初值对于模型参数的反演结果影响不大。当选取初值偏差达到50%时，污染物的降解系数K与真值相当接近，相对误差仅为0.7%；而当初值偏差达到100%时，K的反演误差为8.6%，在允许的误差范围内，充分说明初值对于梯度正则化反演模型参数影响较小。

3.4 测量误差对参数重构的影响

即使是精密仪器测量的观测数据也会有误差，为了更真实地重构模型参数，考虑不同随机噪声对反演结果的影响。采用下述形式表示含有测量误差的观测数据[21]：

表2 不同初值下常系数模型参数重构结果

ρδ(x,T)=ρ(x,T)[1+δrandom(x)]

(25)

式中：ρδ(x,T)为带有测量误差的观测数据；random(x)为一随机函数。初值取u=10 km/h，Ex=6 km2/h，K=0.02 h-1，试验30次的平均结果见表3。

不同噪声水平的常系数模型参数重构结果表明，当测量误差δ为5%时，降解系数K均值的相对误差为0.4%，标准差为0.002 6；当噪声水平δ为20%时，降解系数K反演结果均值的相对误差为20%，标准差为0.005 5，反演结果在合理的范围内，并且迭代次数对于反演结果影响不大，故梯度正则化对于一维常系数河流模型多参数重构是有效的。

4 变系数模型的多参数重构

4.1 线性相关的变系数模型多参数重构

对于顺直河道，水质模型中的参数往往都为常数，然而对于天然河道，水质模型参数都是变化的，并且参数之间可能存在较强的耦合性。假设河道的平均流速为空间位置的线性函数(如明渠渐变流)u=ax+b，而根据费希尔的估算公式，弥散系数为河道平均流速的二次函数,即Ex=βu2。如果平均流速函数已知，则需要重构的模型参数有系数β和污染物的降解速率K，河流污染模型其他参数参考常系数模型的参数值。采用孪生实验，假设u=0.2x+5，β=0.08，采用Crank-Nicolson的有限差分格式求解的结果(图2)作为终端观测值基础。

图2 Crank-Nicolson格式求解的变系数模型不同时刻浓度

4.1.1 初值对参数重构的影响

选择不同的初值，求解精度EPS取10-4，变系数模型多参数重构的结果见表4，其中x*为精确值。从表4中可以得出，不同的初值和迭代次数对反演结果的影响较小。究其原因可能是反演的参数本身数量级较小，对于重构结果影响不大。

4.1.2 测量误差对参数重构的影响

由于观测数据可能存在一定的测量误差，应用梯度正则化迭代结果也会产生相应的误差。为确定测量误差对参数重构的影响，选择初值β=0.12,K=0.03 h-1，表5为不同测量误差下变系数模型参数重构结果。当测量误差为20%时，重构参数的均值为β=0.082 0，K=0.1 587 h-1；均值的相对误差分别为2.5%、5.8%；标准差也较小，分别为0.006 2、0.001 2，充分说明梯度正则化方法有较大的容错性，适用于天然河道污染水质线性相关模型参数重构。

表3 不同测量误差下常系数模型参数重构结果

表4 不同初值下线性相关变系数模型参数重构结果

表5 不同测量误差下线性相关的变系数模型参数重构结果

表6 不同初值下线性无关的变系数模型参数重构结果

4.2 线性无关的变系数模型多参数重构

如果变系数模型参数之间不存在耦合性，假设河流的平均流速为u=ax+b，河流污染物的扩散系数为Ex=cx2+dx+e，污染物的降解速率K=0.015,求解精度EPS取10-4，应用梯度正则化方法研究线性无关的变系数模型多参数重构。

4.2.1 初值对参数重构的影响

表6列出了不同初值下线性无关的变系数模型参数的重构结果，从表6中可以看出，初值对反演结果的影响不大。

4.2.2 测量误差对参数重构的影响

类似地，考虑测量误差的影响。初值选择u=0.5x+5，Ex=0.02x2+0.3x+1.0,不同测量误差下线性无关变系数模型参数重构结果见表7。从表中可以得出，当测量误差为5%时，河流平均流速u=0.399x+2.98，污染物弥散系数Ex=0.0167x2+0.243x+0.905；当测量误差为20%时，平均流速u=0.398x+3.04，弥散系数Ex=0.017 1x2+0.23x+0.915，均与真实解u=0.4x+3，Ex=0.016x2+0.24x+0.9很接近。可见，测量误差的影响很小，进一步地证明梯度正则化法稳定性好。

表7 不同测量误差下线性无关的变系数模型参数重构结果

5 结 论

应用Crank-Nicolson格式离散一维河流水质方程，比较梯度正则化法、共轭梯度法以及混合遗传算法重构顺直河流水质模型参数的结果，得出梯度正则化法是一种有效地参数重构方法，进而应用梯度正则化方法重构顺直和天然河流水质模型的多参数。结果表明，不管是顺直常系数河道还是天然变系数(线性相关或线性无关)河道，梯度正则化方法均能有效地联合重构多参数。此外，模拟结果表明，初值和测量误差对模拟结果影响较小，进一步证明梯度正则化方法是一种快速有效的重构河流水质模型参数的方法。

梯度正则化方法不但适用于一维河流水质模型参数的重构，而且可以推广到二维情形，具有较强的通用性。具体问题应用成功的关键在于河流水质模型正问题的求解和优化参数的选取。

[1] 孙培德.环境系统模型及数值模拟[M].北京：中国环境科学出版社,2005.

[2] 王红旗,秦成,陈美阳. 地下水水源地污染防治优先性研究[J]. 中国环境科学, 2011, 31(5): 876-880. (WANG Hongqi, QIN Cheng, CHEN Meiyang.Study on priorities of prevention and control of groundwater source pollution [J]. China Environmental Science, 2011,31(5):876-880.(in Chinese))

[3] 李功胜, 姚德. 扩散模型的源项反演及其应用[M]. 北京：科学出版社, 2014.

[4] YEH W G. Review: optimization methods for groundwater modeling and management [J]. Hydrogeology Journal, 2015, 23(6): 1-15.

[5] 轩晓博, 逄勇, 李一平, 等．金属矿区重金属迁移对水体影响的数值模拟[J]. 水资源保护，2015, 31(2): 30-35. (XUAN Xiaobo, PANG Yong, LI Yiping, et al. Numerical simulation of influence of heavy metal migration on water in metallic mining areas [J]. Water Resources Protection, 2015, 31(2):30-35. (in Chinese))

[6] 江思珉,张亚力,蔡奕,等. 单纯形模拟退火算法反演地下水污染源强度[J]. 同济大学学报(自然科学版), 2013, 41(2): 253-257. (JIANG Simin, ZHANG Yali, CAI Yi, et al. Groundwater contamiant identification by hybrid simplex method of simulated annealing[J]. Journal of Tongji University (Nature Science), 2013, 41(2): 253-257. (in Chinese))

[7] HAZART A, DUBOST S, GIOVANNELLI J F, et al. Erratum to “inverse transport problem of estimating point-like source using a Bayesian parametric method with MCMC” [J]. Signal Processing, 2014, 96(5):346-361.

[8] 肖传宁,卢文喜,安永凯,等. 基于两种耦合方法的模拟-优化模型在地下水污染源识别中的对比[J]. 中国环境科学, 2015, 35(8): 2393-2399. (XIAO Chuanning, LU Wenxi, AN Yongkai, et al. Simulation-optimization model of identification of groundwater pollution sources based on two coupling method[J]. China Environmental Science. 2015,35( 8): 2393-2399. (in Chinese))

[9] 朱嵩,毛根海,刘国华.基于FVM-HGA的河流水质模型多参数识别[J].水力发电学报, 2007, 26(6):91-95. (ZHU Song, MAO Genhai, LIU Guohua. Parameters identification of river water quality model based on finite volume method-hybrid genetic algorithm[J]. Journal of Hydroelectric Engineering, 2007, 26(6): 91-95. (in Chinese))

[10] 薛红琴,赵尘,刘晓东,等.确定天然河流纵向离散系数的有限差分-单纯形法[J].解放军理工大学学报(自然科学版), 2012, 13(2): 214-218. (XUE Hongqin, ZHAO Chen, LIU Xiaodong, et al. Finite difference method: simplex method for the determination of longitudinal dispersion coefficient in natural rive[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2012, 13(2): 214-218. (in Chinese))

[11] 江思珉,王佩,施小清,等.地下水污染源反演的Hooke-Jeeves吸引扩散粒子群混合算法[J]. 吉林大学学报(地球科学版),2012,42(6):1866-1872.(JIANG Simin, WANG Pei, SHI Xiaoqing, et al. Groundwater contaminant source identification by hybrid Hooke-Jeeves and attractive repulsive particle swarm optimization method [J].Journal of Jilin University (Earth Science Edition), 2012,42(6):1866-1872.(in Chinese))

[12] 邢利英,张国珍.基于改进的共轭梯度法重构地下水污染源项 [J]. 水资源保护,2017, 33(3):42-46.(XING Liying, ZHANG Guozhen. Reconstruction of the groundwater pollution source with improved conjugate gradient algorithm [J]. Water Resources Protection, 2017, 33(3):42-46. (in Chinese))

[13] LI Z, MAO X Z. Global multi-quadric collocation method for groundwater contaminant source identification [J]. Environmental Modelling & Software, 2011, 26(12): 1611-1621.

[14] 李子, 毛献忠, 周康. 污染物非恒定输运逆过程反演模型研究[J]. 水力发电学报, 2013, 32(6): 115-121. (LI Zi, MAO Xianzhong, ZHOU Kang. Inversion model for the inverse process of unsteady pollutant transport [J]. Journal of Hydroelectric Engineering, 2013, 32(6): 115-121. (in Chinese))

[15] 李功胜, 姚德, 马昱, 等. 一维溶质运移源 (汇) 项系数反演的迭代正则化算法[J]. 地球物理学报, 2008, 51(2): 582-588. (LI Gongsheng, YAO De, MA Yu, et al. An iterative regularization algorithm for determining source (sink) coefficientin 1-D solute transportation [J]. Chinese Journal of Geophysics, 2008, 51(2): 582-588. (in Chinese))

[16] 范小平, 李功胜. 确定地下水污染强度的一种改进的遗传算法[J]. 计算物理, 2007, 24(2): 187-191. (FAN Xiaoping, LI Gongsheng. An improved genetic algorithm for groundwater pollution [J]. Chinese Journal of Computational Physics, 2007, 24(2): 187-191.(in Chinese))

[17] 刘进庆,李功胜,马昱. 确定地下水污染强度的梯度正则化方法[J]. 山东理工大学学报(自然科学版), 2007, 21(2): 17-20. (LIU Jinqing, LI Gongsheng, MA Yu. Gradient-regulation method for determining a pollution source term in groundwater [J].Journal of Shandong University of Technology (Natural Science Edition), 2007, 21(2): 17-20. (in Chinese))

[18] 王福军. 计算流体动力学分析：CFD软件原理与应用[M].北京：清华大学出版社，2004.

[19] 刘继军. 不适定问题的正则化方法及其应用[M]. 北京：科学出版社，2005.

[20] 孙志忠.偏微分方程数值解法[M]. 北京：科学出版社，2005.

[21] DENG Zuicha, QIAN Kun, RAO Xiaobo, et.al. An inverse problem of identifying the source coefficient in a degenerate heat equation [J]. Inverse Problems in Science and Engineering, 2014, 23(3): 498-517.

Reconstruction of river water quality model parameters with gradient regularization approach

XING Liying1, 2, SUN Sanxiang1, ZHANG Guozhen1

(1.SchoolofEnvironmentalandMunicipalEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China; 2.AcademyofCivilEngineeringandArchitecture,NanyangNormalUniversity,Nanyang473061,China)

In order to identify the parameters of the river water quality model, we adopted the Crank-Nicolson finite difference scheme to discrete the control equations first, and then appended several additional terminal observations, and designed an effective gradient regularization algorithm to reconstruct the model parameters. Numerical results show that for both the constant coefficient model of straight channels and the natural coupled or non-coupled variable coefficient model, the proposed method can quickly and effectively identify the model parameters. In addition, the influences of the initial value and measuring error are insignificant, which further demonstrates that the gradient regularization algorithm is effective to inverse the parameters of the river water quality model.

water quality model; model parameter；parameter reconstruction; Crank-Nicolson；gradient regularization

10.3880/j.issn.1004-6933.2017.04.009

国家自然科学基金(51468033)

邢利英(1980—)，女，讲师，博士研究生，主要从事环境水力学的反问题研究。E-mail: lyxing2011@163.com

张国珍，教授。E-mail: guozhenzhang163@163.com

X523

A

1004-6933(2017)04-0055-07

黑臭水体评价方法比较(

2016-11-03 编辑：王 芳)