变径管周向导波Lamb波传播特性

何跃斌，陈 果，卢 超，肖佳辰，石文泽，陈 尧

(南昌航空大学 无损检测技术教育部重点实验室, 南昌 330063)

变径管周向导波Lamb波传播特性

何跃斌，陈 果，卢 超，肖佳辰，石文泽，陈 尧

(南昌航空大学 无损检测技术教育部重点实验室, 南昌 330063)

对周向导波Lamb波在变径管中的传播特性进行了研究。通过仿真软件WAVE 3000选取检测变径管所用探头的楔块角度。针对不同倾斜角度的变径管，分析了周向Lamb波的传播特性，研究了不同激励频率的周向Lamb波在变径管中的传播特性，分析了超声接收信号频散、信噪比等特性，并给出了激励信号的最佳周期数，给变径管周向导波检测提供借鉴。

变径管；周向导波；Lamb波；超声传播

管道系统被广泛应用于天然气、热力、石油等领域中，由于受高温、高压和腐蚀性等恶劣环境的影响，通常管道会出现热疲劳损伤和腐蚀，极易造成安全隐患和经济损失。

超声导波技术应用于管道系统的缺陷检测和健康评估中，具有快速、可靠、长距离、大范围、经济且无需外包等优点，可以优化参数并提高缺陷的识别能力。在管道中传播的超声导波的类型分为两种：一种是沿着管道轴向传播的导波，称为轴向导波，轴向导波主要用于管道轴向的长距离检测，一次传播可达百米以上，但对于厚壁管道，则存在超声衰减相对较大、检测能力不足、波形复杂、缺陷信号识别困难且存在盲区等缺点，其主要包括纵向模态、扭转模态和弯曲模态等；另一种是沿管道周向传播的导波，称为周向导波，周向导波主要包括周向Lamb型导波和周向SH型导波。两种类型的周向导波检测原理如图1所示，周向导波的轴向传播距离有限，但对于大管径缺陷的检测十分有效。周向导波由单个传感器就能产生，不仅能实现沿管道周向的全覆盖检测，还对管壁内的小缺陷或细微裂纹非常敏感[1]。基于以上特点，周向导波十分适合对厚壁管材的微小缺陷进行检测[2]。

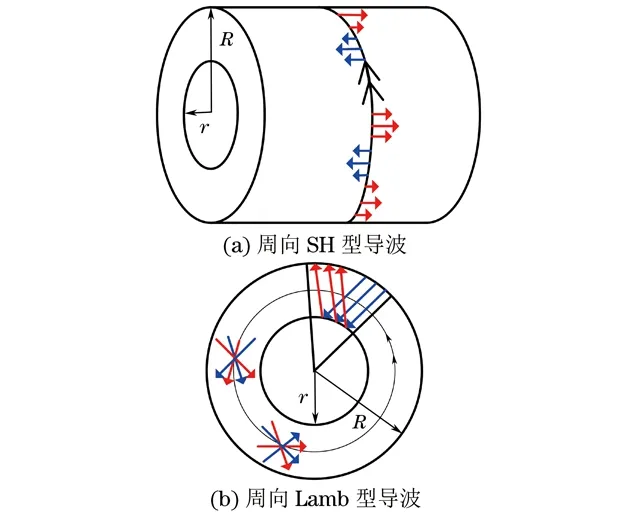
图1 两种类型的周向导波检测原理示意

目前，针对管道的纵向超声导波检测方法的研究比较深入，ALLEYNE、MOON等[3-4]将纵向超声导波检测技术应用于沿管道周向分布的缺陷(裂纹)检测。宋振华等[5]对充液管道和空管的检测进行了对比研究，比较了纵向超声信号和频散曲线的差异以及幅值和群速度的降低程度，分析了充液管道特有的一些相关特性。LOWE等[6]研究了纵向导波对管道上长度与深度变化的槽状缺陷的敏感程度。ROSE、杨胡、汤立国等[7-9]对纵向导波技术应用于管道裂纹的检测进行了研究。

随着周向导波技术在管道检测中的广泛应用，国内外学者也进行了相关的理论和试验研究。最初，1966年，GRACE等[10]建立了空心圆柱体中周向导波的传播模型，将圆柱体置于水中，对周向导波的传播速度和衰减系数进行了相关研究。1999年，LEFEBVRE等[11]从正交各向异性材料出发，得到了管道中的周向导波频散曲线，对群速度频散曲线及波结构进行了分析，找到了检测正交各向异性管的最优频率及相对应模态，而且认为在均匀管道中，径厚比的变化对周向导波的影响很大。近年来，国内对周向导波在厚壁管道方面的研究日益增多，吴斌等[12]优化选取了适合厚壁管道检测的探头和楔块的斜探头组合，该结果为厚壁管道中周向导波的传播特性研究,以及利用周向导波技术对厚壁管道进行无损检测奠定了一定的基础。此外，2015年，葛建明等[13]提出了一种快速检测缺陷的周向导波检测法，分析了探头频率和压电晶片尺寸对检测的影响，并且搭建了试验平台,对缺陷进行了检测与成像。

综上所述，虽然厚壁管道导波检测的相关理论和试验已经比较成熟，但是针对厚壁管道的连接件—变径管的导波理论和试验还缺乏相关的技术和理论支持。为此，笔者以锥形变径管为研究对象，通过仿真对周向Lamb波激励角度进行了选取，并且针对不同倾斜角度变径管的传播特性给予分析；搭建了试验平台，对周向Lamb波的探头楔块角度、激励周期数等传播特性进行了分析。

1 检测方案设计

系统组成如图2所示，检测方式为一发一收双探头模式。该检测系统由计算机(基于LabVIEW信号控制采集软件)、NI数据采集器、高功率超声信号发射接收器(JPR600C)、角束导波探头、变径管等部分组成。该系统最重要的部分是高功率超声信号发射接收器，其中发射频率的调节范围为30 kHz～10 MHz，增益为80 dB，角束导波探头由直探头和有机玻璃楔块组成，斜探头与管壁的耦合采用水解耦合剂。其中，变径管大管径端外径为250 mm、小管径端外径为100 mm，壁厚为30 mm。变径管结构如图3所示。

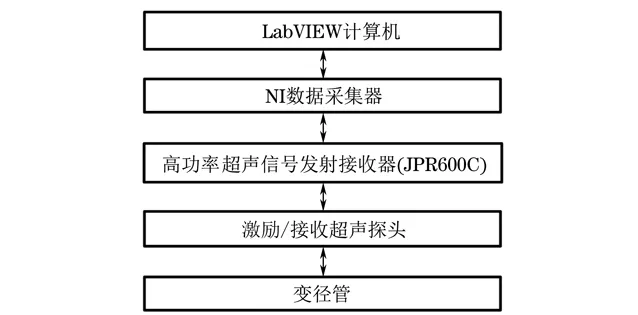
图2 检测系统组成示意

图3 变径管结构示意

2 恒径管中周向导波的传播

为了得到超声导波在有界面各向同性介质中波动方程的解，首先要了解无限大介质中超声波的传播特性，AULD[14]根据牛顿第二定律，得到三维弹性体中的运动方程，其通过分析周向导波的传播问题得出质点的位移矢量是关于径向与周向上的函数，在轴向上的质点位移仅沿轴向平面方向。

对于空心圆柱体中周向导波的传播情况，空心圆柱体的几何结构如图4所示，在空心圆柱中，内外径大小分别为a和b。其边界条件为

(1)

式中：r=a或r=b；θ为圆的极角;σ为应力。

对于空心圆柱体中传播的周向导波，假设其位移为：

(2)

而uθ=uθ(r,θ),uz=0,利用弹性动力学知识以及边界条件进行推导，可以得到导波模态的频散方程为

(3)

式中：D为4×4的矩阵，是频率ω、波数k的函数，并且与管径的尺寸(即内径a、外径b)和材料有关。

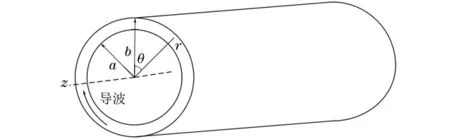
图4 空心圆柱体的几何结构示意

在周向导波的传播过程中，传播特性主要与介质材料、激励频率、周期数、管径尺寸等因素有关。其中，在管径尺寸中，一般情况下，管道的内外径之比不同[15]，则周向导波频散曲线的求解也不同，得到的频散曲线也不一样。也就是说，内外径之比是影响周向导波传播特性至关重要的一点。此外，需要说明的是在周向导波中的Lamb波的传播特性中，弹性场在z坐标方向上的位移为0，即轴向位移为0。

文章研究在介质材料、管径尺寸不变的情况下，变径管中周向导波Lamb波的激励频率、压电晶片角度、激励周期数等对导波传播的影响。

3 数值模拟

有限差分数值模拟广泛应用于模拟波的传播中，其中，超声波仿真软件WAVE3000是一个独立的计算机软件，其可用于求解几乎所有的三维超声波(弹性波传播)问题，能在声学分析上获取多种空间和时间中接收到的模拟波形。利用WAVE3000，用户可以清晰地观察超声波在工件中的传播路径，在获取足够的理论了解以后再应用于实际操作，可以达到事半功倍的效果。此外，WAVE3000具有一些特性，其能够提供完整的粘弹性波动方程的时域解，可以对任意像素的三维实物进行描述，可设置无限(吸收)边界条件、支持批量处理等。

WAVE3000仿真模拟的具体声学方程为

(4)

式中：ρ为材料密度；λ为一阶拉梅系数；μ为二阶拉梅系数；η为剪切黏度；φ体积黏度；t为时间；为梯度算子；·为散度算子；∂为偏微分方程算子。

式(4)适用于各向同性的弹性区域。

除此之外，ω为三维向量，其分量分别是质点在x,y,z三个方向上的位移，即：

(5)

3.1 不同激励下的传播特性

通过WAVE3000软件对周向Lamb波在变径管中的传播进行了模拟仿真试验。考虑计算效率和实验室计算机的配置等问题，仿真试验变径管的尺寸取大管径端至小管径端的垂直方向长度20 mm的一段进行数值模拟，也就是柱面坐标z轴的范围为0～20 mm。信号发射源采用半径为10 mm的圆形发射源，圆形中心位置柱面坐标为(123.75,0,10)。信号为5周期高斯窗调制的正弦脉冲信号，激励信号频率为500 kHz，信号持续振动10 μs，仿真时间为100 μs。变径管三维模型如图5所示。

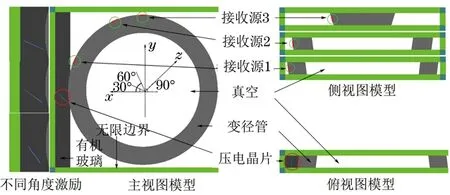
图5 变径管三维模型示意

分别采用30°，45°，60°三种不同入射角度的压电晶片作为激励信号。3个圆形接收源中心的柱面坐标分别为(123.75,30,10)、(123.75,60,10)、(123.75,90,10)，圆形接收源半径都为2 mm。虽然所建模型为三维立体，但只能显示某一个切面的波场快照，文中所选波场快照均为激励源正中心所在切面。得到不同传播时间、不同晶片角度激励下的变径管波场快照如图6～8所示。

图7 45°压电晶片激励下的波场快照

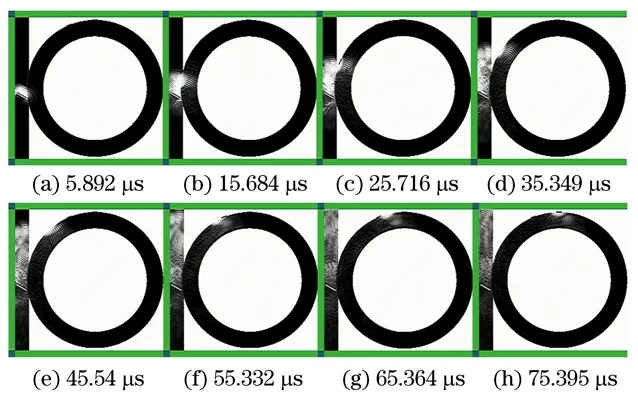
图8 60°压电晶片激励下的波场快照

从图6～8中可以看出，当压电晶片激励信号时，超声波经过有机玻璃与变径管界面时，一部分声波反射回来，被有机玻璃左边的无限边界所吸收；另一部分声波透射进入钢管，在变径管的内外壁往复地反射以及波形转换，形成周向Lamb波在变径管中传播。经过对比发现，3种不同入射角度的晶片有较大差异，该差异也会直接影响周向Lamb波在变径管缺陷检测中的应用。30°压电晶片激励信号在变径管中周向Lamb波的波包较宽、频散严重，不利于实际检测；45°压电晶片在变径管中周向Lamb波的波包比较集中，在传播过程中声场覆盖整个壁厚，有希望实现厚壁管道的缺陷检测；60°压电晶片在周向Lamb波中刚开始传播时，波包比较集中，声场覆盖整个壁厚，但传播一定距离时，声束主要覆盖管道外表面至中部附近，内表面附近声场很弱。

进一步分析不同角度压电晶片对检测产生的影响，分别对30°，45°，60°压电晶片的接收源1、接收源2、接收源3进行分析，其不同接收源所接收波形如图9所示。

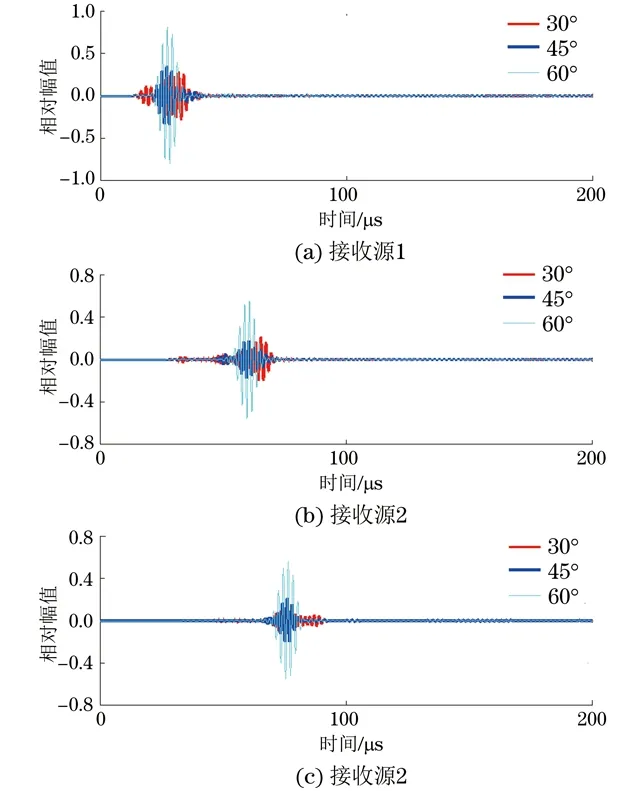
图9 不同晶片角度、不同接收源所接收的波形

从图9可知：30°激励信号的波包很宽，且波包宽度随传播距离逐渐增加，同时，主要传播模式附近存在较多其他模式的导波，不适合采用该角度探头检测变径管；45°和60°压电晶片激励信号在变径管中形成的周向Lamb波波包单一，信号较圆滑，所存在的几种模式以一个包络进行传播，其他模式导波对检测的影响较小，检测变径管可采用楔块角度为45°和60°的探头，也可以采用45°～60°之间任意角度的探头。

3.2 不同倾斜角度变径管的传播特性 压电晶片采用半径为3 mm的圆形发射源，角度为55°。a、b、c接收源轴向分布在变径管表面(a为大管径端接收源，b为中间接收源，c为小管径端接收源)，接收源都在压电晶片顺时针旋转90°的位置，圆形接收源中心的柱面坐标为：恒径管a(123.75,90,5)、b(123.75,90,10)、c(123.75,90,15)，变径管a(124.375,90,5)、b(123.75,90,10)、c(123.125,90,15)，45°变径管a(128.75,90,5)、b(123.75,90,10)、c(118.75,90,15)，60°变径管a(132.41,90,5)、b(123.75,90,10)、c(115.09,90,15)。其中，变径管圆形接收源半径都为2 mm。不同倾斜角度变径管模型如图10所示，图10(a)为激励源正中心所在切面，这时切片显示的是b接收源，图10(b)为a、b、c接收源的具体位置。

图10 不同倾斜角度变径管模型

为了清楚看出不同倾斜角度的变径管对接收波形的变化情况，对a、b、c接收源所接收波形进行比较分析(见图11)。

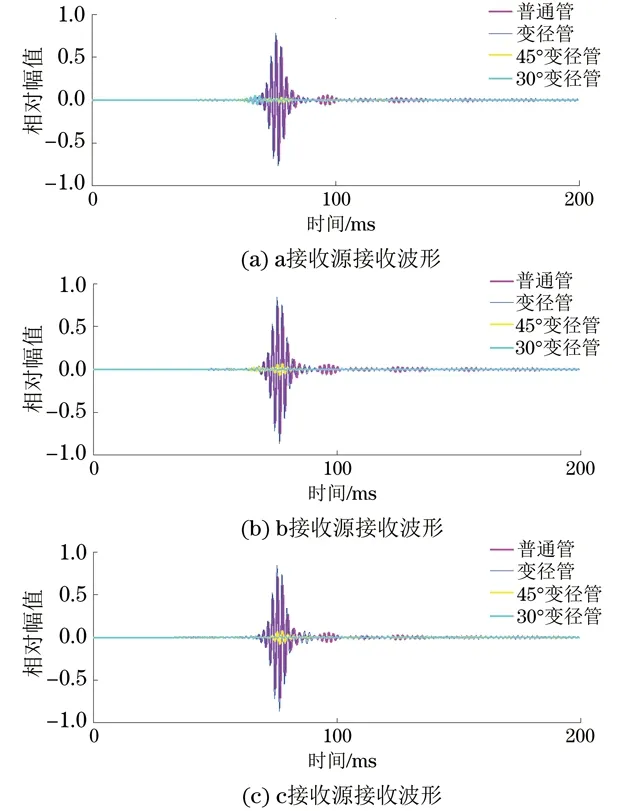
图11 不同倾斜角度变径管的接收波形

由图11可知，整体上看，周向Lamb波在恒径管和变径管中传播时，其模态发生转换，模态的成分发生变化。比较恒径管与变径管a、b、c接收源接收到的波形，变径管接收波包减少，主波形的幅值略微增大，这是由于发生了模态转换，几种模态形成的两个波包变为一个波包，能量更集中。随着变径管的倾斜角度越来越大，能量逐渐减小。当变径管的倾斜角度为45°，60°时，a、b、c接收源接收到的幅值都有很大幅度地减小，形成很多波包，整体波包变宽、频散严重。

对同一管子a、b、c接收源接收能量及频散程度进行分析，得到不同管子的不同接收源接收的波形对比图(见图12)。

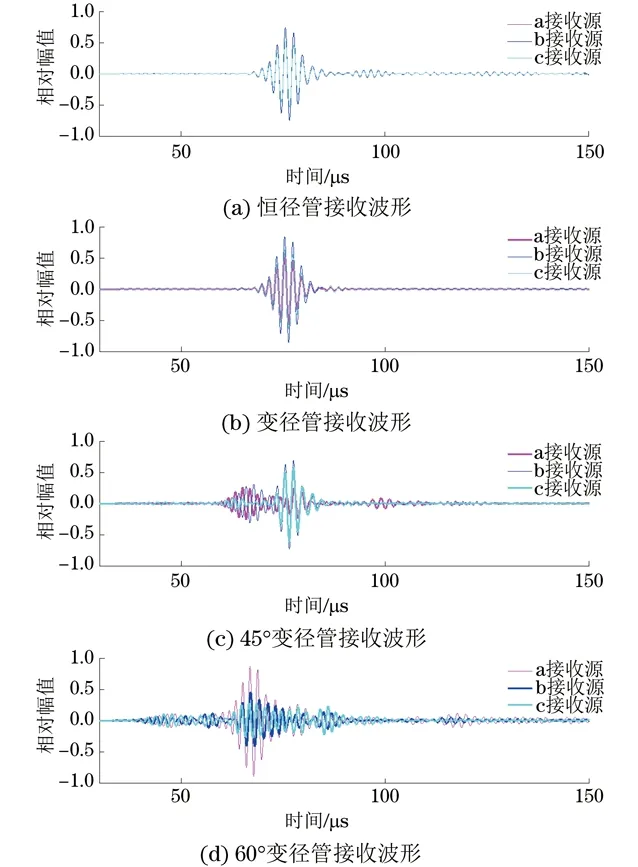
图12 不同管子的不同接收源接收的波形

由图12可知，当变径管的倾斜角度较小时，接收到的波形变化不大，模态较少，有利于进行缺陷检测；当变径管的倾斜角度较大时，其接收到的波形模态较多、能量分散、频散严重，不利于进行缺陷的识别。当管子为恒径管时，接收源接收波形幅值大小依次为b>a=c；当管子为变径管时，接收源接收波形幅值大小依次为b>c>a；当管子为45°变径管时，接收源接收波形幅值大小依次为b>c>a；当管子为60°变径管时，接收源接收波形幅值大小依次为a>b>c。综上所述，当变径管的倾斜角度为0°～45°时，其b接收源接收的幅值最大，压电晶片激励源正中心所在切面的接收源接收的能量最强。变径管半径较小的小头端c接收源接收的波形幅值大于半径较大的大头端a接收源所接收的波形幅值。也就是说，当周向导波在变径管中传播时，由于径厚比发生变化，其接收的超声波轴向能量发生了改变。检测缺陷时，应该尽量使压电晶片正中心所在切面与缺陷正中心切面重合，或者让压电晶片正中心所在切面偏向缺陷正中心的大管径端。

4 变径管中超声导波的传播特性

超声导波在管道中传播时会发生频散现象和多模态特征，同时会出现多个模态互相干涉的现象，导致信号识别存在困难，文中所有信号都是经过Chirp(编码脉冲技术)调制处理的信号。通过周向导波Lamb波在变径管中传播特性的分析，得到最优的检测信号，双探头实物连接外观如图13所示，待测试样为壁厚30 mm、大管径端外径250 mm、小管径端外径100 mm的变径管，将激励/接收压电换能器分别置于厚壁管道外表面距大管径端60 mm处，且相对周向距离为200 mm处。采用一发一收双探头模式，试验时确保楔块与变径管表面耦合良好。

图13 双探头实物连接外观

4.1 不同激励下的传播特性 采用500 kHz和700 kHz两种激励频率，楔块角度分别取37°，45°，55°，周期数为9。为了方便比较，分别设置参数为：激励频率500 kHz，楔块角度55°，不加增益；激励频率700 kHz，楔块角度55°，增益设为5 dB；其他不同频率、不同角度的探头增益均为10 dB。激励频率分别为500，700 kHz，不同楔块角度激励信号的包络波形如图14～15所示。

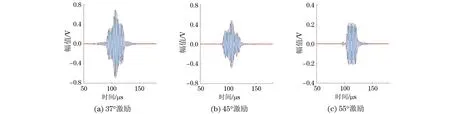
图14 激励频率500 kHz、不同楔块角度激励信号的包络波形

图15 激励频率700 kHz、不同楔块角度激励信号的包络波形

通过图14和图15可知，当激励频率为500 kHz时，由于楔块为55°时不加增益，跟其他角度楔块相比，此时的幅值最大、波包宽度最小，说明频散程度小、模态少、信噪比最小，有利于实际检测；37°楔块斜探头的幅值其次，这时的波包宽度最大、模态多、不利于检测；45°楔块斜探头的幅值最小。当激励为700 kHz时, 55°楔块斜探头的幅值最大，37°楔块斜探头的幅值其次，45°楔块斜探头的幅值最小。所以，当激励频率为500 kHz时，45°和55°楔块斜探头适合对变径管进行检测。同时,也验证了仿真的准确性。当激励频率为700 kHz时，楔块角度为37°，45°，55°时都存在频散、模态多、波包宽等现象，不适合对变径管进行检测。

4.2 不同周期下的传播特性

采用500 kHz和700 kHz两种激励频率，楔块角度都选取为55°，周期为1，3，5，7,9,12,14,16,18,20。其中，激励频率为500 kHz的压电晶片不加增益，激励频率为700 kHz的增益调整为5 dB。得到激励信号周期数与幅值、波包宽度的关系，如图16所示。

由图16(a)可知：当激励信号周期数为1时，激励频率为500 kHz的波包幅值为0.107 3 V，激励频率为700 kHz的波包幅值为0.048 V；当激励信号周期数增长到20时，频率500 kHz的波包幅值为0.233 8 V，频率700 kHz的波包幅值为0.067 2 V。总之，激励频率为500 kHz和700 kHz的波包幅值都是随着激励信号周期数的增大相应增大，然后趋于平稳。当激励信号频率为500 kHz时，幅值开始增长得比较快，而频率为700 kHz信号的幅值比较稳定。由图16(b)可知：当激励信号周期数为1时，500 kHz的波包宽度为14.5 mm，700 kHz的波包宽度为41.7 mm；当激励信号周期数增长到20时，500 kHz的波包宽度为46 mm，700 kHz的波包宽度为74.1 mm。两种频率的波包宽度会随着激励信号周期数的增大，总体呈增大趋势。由于波包的宽度与检测分辨率息息相关，因此检测时激励信号的周期数也不宜过高。所以，从检测时信号的分辨率和信噪比两方面考虑，取7～12周期为检测变径管的最佳周期数。

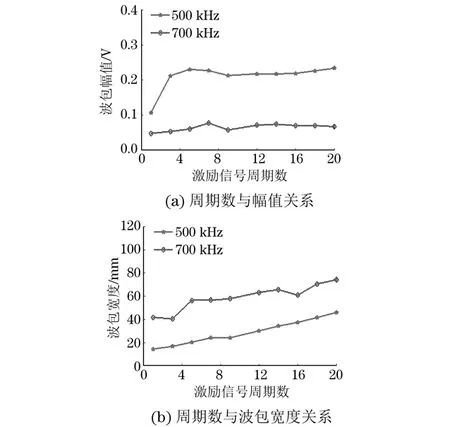
图16 激励信号周期数与幅值、波包宽度的关系曲线

5 结论

(1) 楔块角度是影响变径管导波检测的重要因素。当确定楔块角度为45°和60°时，周向导波Lamb波波包集中，而且楔块角度为60°时可以对中外壁进行检测，楔块角度为45°时可以对整个壁厚进行检测。

(2) 变径管倾斜角度决定其周向Lamb波检测的难易程度。当变径管倾斜角度较小时，其主模态变化小。虽然模态成分发生改变，但是可以周向Lamb波对变径管进行检测。与恒径管相比，当检测变径管时，径厚比发生变化，其接收的超声波轴向能量发生了改变。应该尽量使压电晶片正中心所在切面与缺陷正中心切面重合，或者让压电晶片正中心所在切面偏缺陷正中心的大管径端。随着变径管倾斜角度的增大，当变径管的倾斜角度为45°和60°时，接收源接收波形幅值大幅减小、模态增多、波包很宽、频散严重，很难采用周向Lamb波对其进行检测。

(3) 激励频率的影响在变径管导波检测中起着重要作用，在周期等其他条件不变的情况下，将500 kHz与700 kHz激励频率所传播接收的信号进行对比，激励信号为500 kHz时所接收的波形幅值大，且频散小、波包宽度小，楔块角度为45°和55°的斜探头能对变径管进行检测。激励信号为700 kHz时幅值小、频散严重、对检测效果不好，接收缺陷波形容易与周向导波波形混合，造成漏检。

(4) 对于试验所涉及的待测试样，激励频率为500 kHz时，无论激励频率是500 kHz还是700 kHz，检测变径管周向Lamb波信号最佳检测周期选取为7～12。

[1] GAO W, GLORIEUX C, THOEN J. Study of circumference waves and their interaction with defects on cylindrical shells using line-source laser ultrasonics[J]. Journal of Applied Physics, 2002,91(9):6114-6119.

[2] LIU Y, LI Z, GONG K. Detection of a radial crack in annular structures using guided circumferential waves and continuous wavelet transform[J].Mechanical Systems and Signal processing, 2012,30(7):157-167.

[3] ALLEYNE D, CAWLEY P. The long detection of corrosion in pipes using lamb waves[J]. Review of Progress in Quantitative Nondestructive Evaluation, 1995, 14: 2073-2080.

[4] MOON H P, IN S K, YOUNG K Y. Ultrasonic inspection of long steel pipes using Lamb waves[J]. NDT&E International, 1996, 29(1): 13-20.

[5] 宋振华, 王志华, 黄世清, 等. 基于纵向超声导波信号特性的管道损伤检测研究[J]. 机械强度, 2011,33(1): 55-61.

[6] LOWE M J S, ALLEYENE D N, CAWLEY P. Defect detection in pipes using guided waves[J]. Ultrasonics, 1998, 36(1): 147-154.

[7] ROSE J L, HONGERHOLT D D, SAMES D J. Laser based guided wave experiments for tubing[J]. Experimental Mechanics, 1997, 37(2):165-168.

[8] 杨胡, 王成.管道裂纹纵向超声导波检测仿真研究[J].中北大学学报(自然科学版),2006,27(4):348-351.

[9] 汤立国, 程建春, 王金兰. 管道中激光激发瞬态导波的理论研究[J].声学学报,2001, 26(6): 489-496.

[10] GRACE O D, GOODMAN R R. Circumferential waves on solid cylinders[J]. The Journal of the Acoustical Society of America,1966,39(1): 173-174.

[11] LEFEBVRE J E, ZHANG V, GAZALET J, et al. Legendre polynomial approach for modeling free-ultrasonic waves in multilayered plates[J]. Journal of Applied Physics, 1999,85(7): 3419-3427.

[12] 吴斌, 颉小东, 刘增华. 厚壁管道周向导波检测技术实验研究[J]. 实验力学, 2011,26(5): 625-631.

[13] 葛建明, 刘兴林, 戴翔. 基于周向导波的厚壁管道缺陷检测及成像[J]. 无损检测, 2015, 37(8): 39-42.

[14] AULD B A. Acoustic fields and waves in solids[M]. Malabar:[s.n], 1990.

[15] 黄松岭. 电磁超声导波理论与应用[M]. 北京：清华大学出版社, 2013.

Propagation Characteristics of Circumferential Guided Waves of Taper Pipe

HE Yuebin, CHEN Guo, LU Chao, XIAO Jiachen, SHI Wenze, CHEN Xiao

(Key Laboratory of Nondestructive Testing of Ministry of Education, Nanchang Hangkong University, Nanchang 330063, China)

In this paper, the propagation characteristics of the taper pipe are studied by the circumferential guided Lamb wave. The wedge angle of the probe used to detect the reducer is selected by simulation software WAVE3000. And the propagation characteristics of the circumferential Lamb waves are analyzed for the different diameters. At the same time, the propagation characteristics of the circumferential Lamb waves with different excitation frequencies in the taper tube are studied, and the characteristics of the dispersion of the

signal and the signal-to-noise ratio are analyzed. The optimal number of excitation signals is given. The above studies provide guidance for circumferential guided wave detection of taper pipe.

taper pipe;circumferential guided wave; Lamb wave; ultrasonic propagation

2016-12-03

国家自然科学基金资助项目(11374134,51265044)

何跃斌(1990-),男,硕士研究生, 主要从事超声无损检测技术研究工作,524529314@qq.com

卢 超(1971-), 男, 教授，主要从事固体声学及超声检测研究工作，luchaoniat@163.com

10.11973/wsjc201707001

TG115.28

A

1000-6656(2017)07-0001-07