基于集总经验模态分解和极坐标表示的瞬时转速诊断方法

王 帅 向 阳 王 磊

1.武汉理工大学能源与动力工程学院，武汉，4300632.船舶动力系统运用技术交通行业重点实验室，武汉，430063

基于集总经验模态分解和极坐标表示的瞬时转速诊断方法

王 帅1,2向 阳1,2王 磊1,2

1.武汉理工大学能源与动力工程学院，武汉，4300632.船舶动力系统运用技术交通行业重点实验室，武汉，430063

为解决瞬时转速方法在诊断多缸中高速V型机发生失火故障时，存在的特征参数难以提取、诊断精度不高等问题，以发火间隔角不均匀的某V12柴油机为对象，进行了基于集总经验模态分解(EEMD)和极坐标表示的诊断方法研究。结果表明：构成本征模态函数IMF6分量的主频率为8.3 Hz(0.5谐次)，经过EEMD分解提取了0.5谐次成分，其幅值可作为判别单缸失火故障的特征值；将0.5谐次相位及其变化规律与极坐标表示结合，能够直观准确地定位故障。

集总经验模态分解；瞬时转速；单缸失火；极坐标表示；故障定位

0 引言

柴油机工作过程中，当气体力矩大于阻力矩时，转速升高；反之，转速下降，缸内燃烧情况会直接体现在瞬时转速(instantaneous angular speed，IAS)中[1]。凭借传感器安装简单、价格便宜、信号信噪比高等一系列优点，瞬时转速诊断方法得到了广泛应用，它可以有效替代缸压监测，对缸内的燃烧情况进行监测诊断。

国内外学者对瞬时转速已进行了大量研究，基于瞬时转速的诊断方法主要是利用现代信号处理方法从时域、频域提取故障特征。文献[2-3]通过提取瞬时转速中的波峰值、波谷值、峰峰值、峰谷值等时域特征参数对柴油机失火、漏油等故障进行诊断；文献[4]根据内燃机动力学理论，提出了基于扭振信号的谐次分析法，并用于缸内燃烧状况分析；文献[5]研究了如何利用0.5谐次诊断失火、单缸功率不足等燃烧故障；文献[6-7]分别运用Winger-Ville分布、STFT变换对瞬时转速进行分析，提取了微弱功率不平衡、失火等故障的特征参数；文献[8-10]使用小波分析和经验模态分解(EMD)来滤除瞬时转速信号中的噪声。

瞬时转速方法在缸数较少、转速不高的机型上已取得了良好的诊断效果，但是当柴油机缸增多(9缸以上)、发火间隔不均匀、转速升高和负载多变时，瞬时转速波动将会变得十分复杂[11]，应用上述研究成果已无法从瞬时转速中提取到直观可靠的故障特征。

集总经验模态分析(ensemble empirical mode decomposition，EEMD)是一种自适应的信号处理方法，非常适合非平稳非线性信号分析。为了消除或减弱谐次诊断中存在的干扰，提取更加敏感的故障特征，本文将EEMD引入到瞬时转速诊断方法中。首先对V12柴油机的瞬时转速信号进行EEMD分解，得到一系列本征模态函数(IMF)分量，然后对比正常与故障工况下的IMF分量，提取敏感特征，最后将特征向量转化为极坐标表示[12]对故障进行定位。

1 基本理论

1.1 谐次理论

在多缸内燃机系统中，每一个气缸都受到一个由若干次简谐力矩所组成的复谐力矩作用，假设轴系在某一振型上振动，则第v次激振力作用下系统输入总能量W为

W=πM1vA1vsinφ1v+πM2vA2vsinφ2v+

式中，M1v，M2v，…，Mkv为各缸第v次简谐力矩幅值；Aiv为第i缸第v次简谐扭振幅值；φiv为第i缸简谐力矩与扭转角位移之间的相位差。

将某缸气体压力pg以θ变化的傅里叶级数展开，即

pg=p0+a1cosθ+a2cos2θ+a3cos3θ+

…+b1sinθ+b2sin2θ+b3sin3θ+…=

式中，p0为气体激励力形成的平均力；v为简谐次数；pv为第v谐次简谐力的振幅；av、bv为傅里叶系数；ψv为v谐次简谐力的初相位。

对四冲程柴油机来说，曲轴每转两周气体激励力矩才变化一次，所以它的圆频率为曲轴角速度的一半，即存在半谐次。由内燃机动力学理论可知，柴油机各缸对应不同的0.5谐次相位，这一规律已在故障定位中得到了广泛应用[5,11]。0.5谐次分量的时域波形在柴油机一个工作循环周期的相位变化为360°，而对应的曲柄转角变化为720°，即每当曲柄转角变化1°，0.5谐次相位变化0.5°。如图1和图2所示，若相邻气缸压力间隔角度为φ，则0.5谐次相位变化β=0.5φ。

图1 相邻两缸气体压力Fig.1 Nearby cylinder pressure

图2 0.5次谐波相位间隔Fig.2 The interval phase of 0.5 harmonic order

1.2 经验模态分解

经验模态分解(EMD)可以把信号分解为有限个不同尺度的IMF分量，数学上，信号x(t)可以表示为N个IMF分量与一个残余项之和，即

式中，rN(t)为残量，代表信号中的平均趋势；cj(t)为IMF分量，代表信号中从高到低不同频率段的成分。

EMD分解得到的各IMF分量具有不同频带特性，其分解的实质相当于使用一组带通滤波器对信号进行滤波。为了说明它的滤波特性，使用EMD对长度为1024的独立高斯白噪声序列进行分解。样本个数为5000，分析各个IMF分量的平均功率谱特性，得到的结果如图3所示，研究表明EMD对白噪声的分解作用等同于一组二进制带通滤波器组[13]。

图3 白噪声经EMD分解后部分IMF分量的功率谱Fig.3 Power spectrum of some IMFs of white noise

为了克服EMD分解过程中存在的模态混叠问题，采用EEMD方法，通过加入白噪声来减弱或消除信号的间断性，分解后获得的IMF分量包括噪声和信号本身。每次分解使用不同的白噪声，当集合平均次数足够多时，噪声会被抵消或减小到足够小的量级(白噪声均值为0)，有用信号被分离出来[14]。

1.3 极坐标表示

一个周期正弦波的极坐标表示如图4所示，图中270°和180°处出现了下陷区(图4中粗虚线内区域)，分别对应正弦波初始相位为0和π/2两种情况。下陷区相位差与初始相位差相等，因此可将下陷区相位作为波形相位的另一种表达方式。

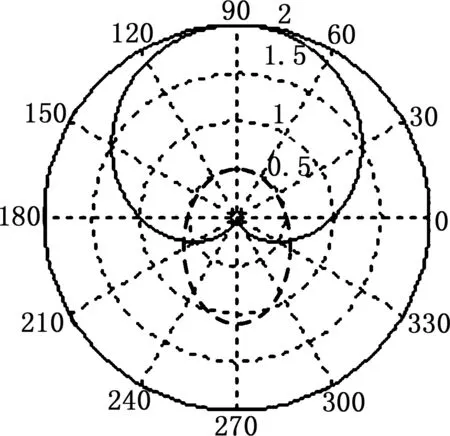
(a) 初始相位0

(b) 初始相位π/2

2 瞬时转速测量和提取

2.1 瞬时转速测量

试验在某V12柴油发电机上进行，其主要技术参数见表1。柴油机在额定转速1000 r/min、25%负荷下运转，分别采集正常和单缸失火工况下的瞬时转速信号与上止点信号，采样频率为51.2 kHz。现场测量如图5所示，瞬时转速传感器正对飞轮齿安装，上止点传感器以B6缸为基准，正对飞轮端面上的尖劈安装，为了判定上止点是否位于燃烧上止点，同步测量了B6缸高压油管脉动信号。

表1 发动机技术参数

(a)12V280ZD柴油机(b)上止点与转速传感器图5 现场测量图Fig.5 Field measurement

2.2 瞬时转速提取

精确提取瞬时转速，是进行监测诊断的前提。ANDRÉ 等[15]指出频域提取方法比过零点法等方法拥有更高的精度，因此本文采取频率解调方法。

首先去除瞬时转速原始电压信号中的均值，然后截取柴油机20个工作循环信号进行频谱分析，结果如图6所示，由图可知，载频是4500 Hz。以载频为中心频率，对原始信号进行带通滤波，通带为[3500,5500]Hz，滤波后信号变成一个典型的单分量调频信号。最后利用Hilbert变换对其进行频率解调，并滤除其中含有的高频噪声。柴油机转速是1000 r/min(发火频率为100 Hz)，通常只需研究到10倍发火频率即可。提取的瞬时转速信号如图7所示。

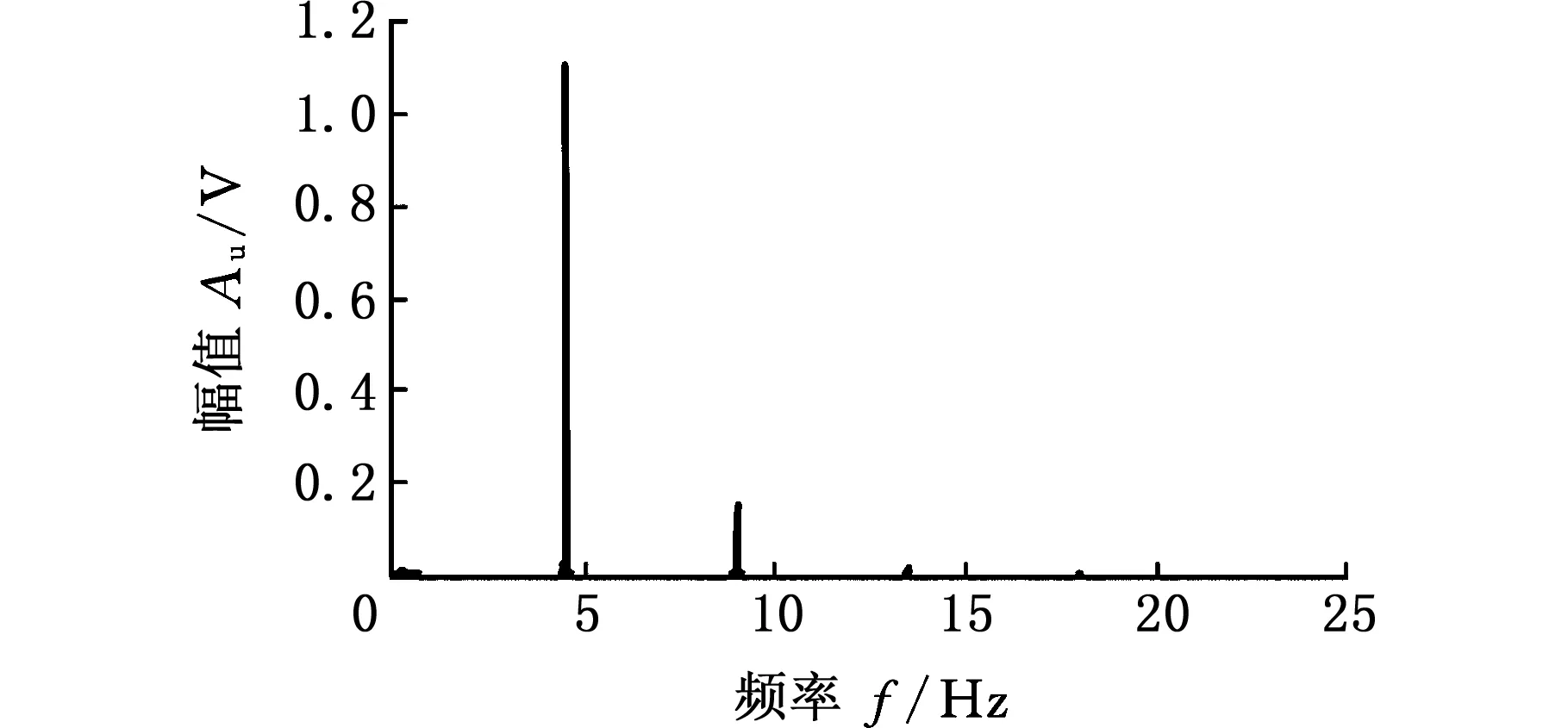
图6 瞬时转速原始电压信号的频谱Fig.6 Spectrum of IAS voltage

图7 基于解调法提取的瞬时转速信号Fig.7 Extracted IAS based on demodulated method

3 基于EEMD方法的故障诊断

3.1 瞬时转速的EEMD分解及故障特征提取

对正常工况下的瞬时转速信号进行EMD分解，得到6个IMF分量和1个残余量，结果如图8所示。对比IMF分量c1(t)和c2(t)可知，两者出现了模态混叠。

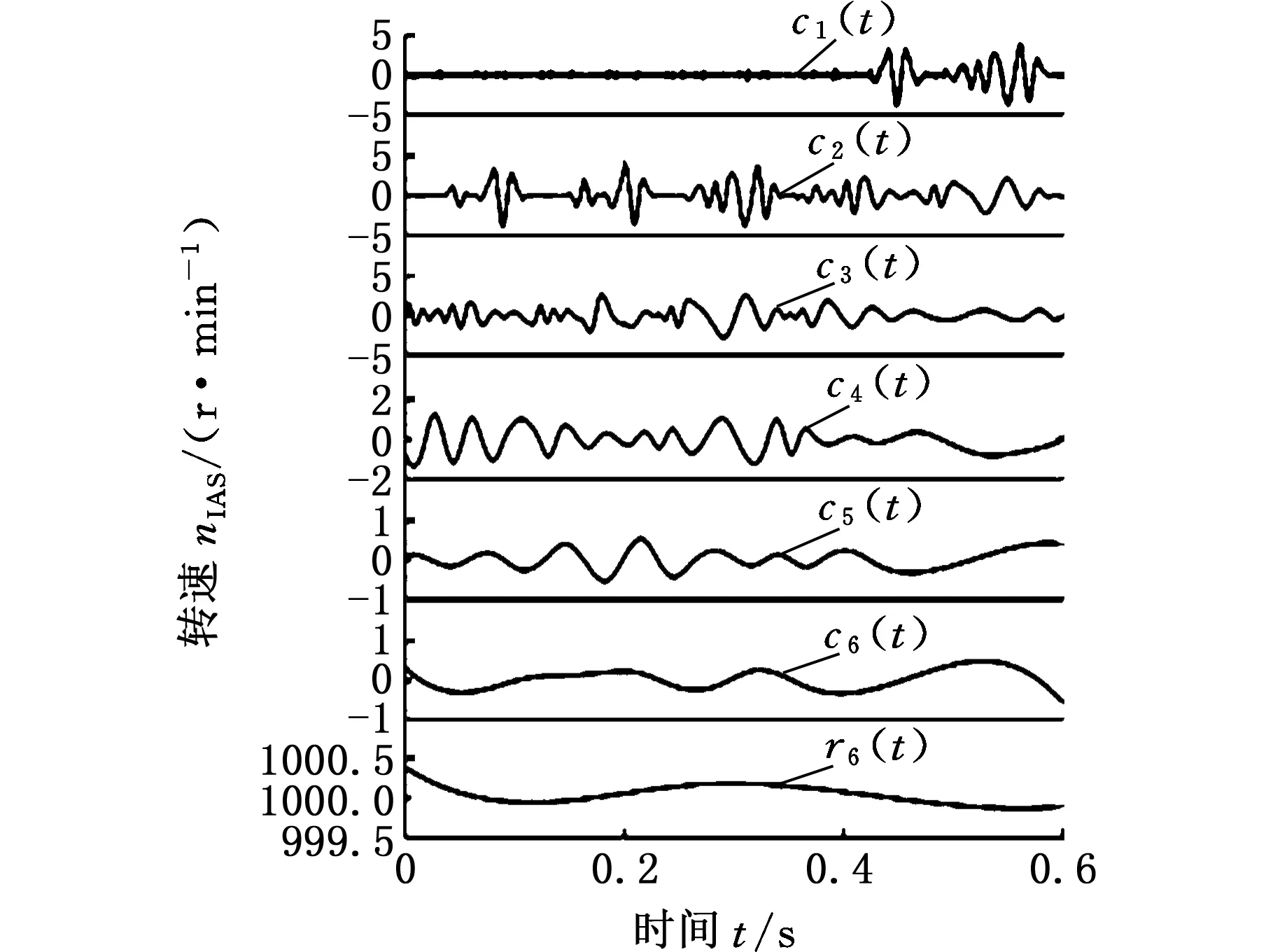
图8 瞬时转速的EMD分解结果Fig.8 EMD of normal IAS signal

为了克服模态混叠，采用EEMD对信号进行分解。噪声幅值系数和添加次数的设定，目前没有定论，本文参考文献[14]，结合瞬时转速信号自身特点并经过反复试验，最终选取幅值系数为0.05，添加次数为300。

图9所示为瞬时转速经EEMD分解后的各IMF分量，其中IMF分量c1(t)为高频分量，对其进行分析处理可以去除信号中的噪声，提高信噪比；IMF分量c2(t)～c6(t)可能是气体激励力矩、往复惯性力矩和发电机负载等因素共同作用产生的分量；r6(t)为残余分量，含有平均转速、滚振和趋势项等信息。

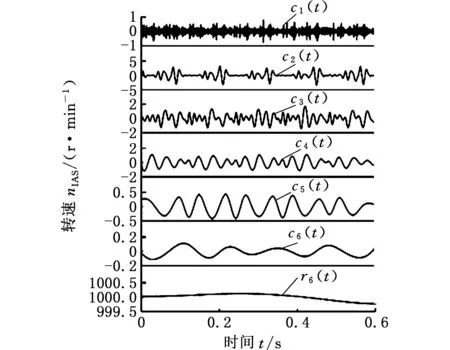
图9 瞬时转速的EEMD分解结果Fig.9 EEMD of normal IAS signal

图10 B1缸失火时瞬时转速的EEMD分解结果Fig.10 EEMD of B1 misfire IAS

对单缸失火故障下的瞬时转速进行EEMD分解，结果如图10所示。与图9正常工况下分解结果进行对比，直接从各分量幅值上可以看出IMF分量c3(t)、c5(t)、c6(t)变化明显。c3(t)幅值变化不到1.2倍，c5(t)幅值大约变化1.5倍，而c6(t)幅值则大约变化2.5倍，因而初步断定c5(t)和c6(t)分量对缸内故障更为敏感。为了更加深入地发掘其中的规律，对正常和B1缸失火工况下的瞬时转速进行HHT时频分析，结果如图11和图12所示。故障工况下，时频图上出现了一条明显的低频带，经分析其大小约为8.3 Hz(0.5谐次)，这与谐次理论分析结果一致。

图11 正常工况下瞬时转速HHT时频图Fig.11 HHT of normal IAS

图12 B1缸失火时瞬时转速HHT时频图Fig.12 HHT of B1 misfire IAS

为了提高频率分辨率，选取柴油机20个工作循环(约2.4s)的数据进行EEMD分解。对分解得到的第5、第6个IMF分量进行频谱分析，结果发现IMF分量6的主频率为8.3 Hz(0.5谐次)，如图13所示，相关干扰因素已被分离开来，0.5谐次分量得以有效提取。正常工况下，瞬时转速IMF分量6中8.3 Hz(0.5谐次)成分的幅值很小，约为0.03 r/min；当发生B1缸失火故障时，瞬时转速IMF分量6中8.3 Hz(0.5谐次)成分的幅值约为0.19 r/min，是正常工况下幅值的6.3倍。由此可知，IMF分量6能够用来判别失火故障，IMF分量6中8.3 Hz(0.5谐次)成分的幅值可以作为失火故障特征值。

图13 B1缸失火时IMF分量6的频谱Fig.13 IMF6 spectrum of B1 misfire IAS

为了验证上述结论的可靠性，分别对不同缸失火故障下的瞬时转速进行EEMD分解，并对其IMF分量6作频谱分析，提取IMF分量6中8.3 Hz(0.5谐次)成分的幅值，结果见表2。分析表2中数据可知，B1缸与A6缸失火故障工况下的幅值是正常工况下幅值的6.3倍，B5缸与B3缸失火故障工况下的幅值是正常工况下幅值的8.7倍，A2缸失火时该幅值介于二者之间。因此合理设置此幅值的阈值，可以实现对单缸失火故障的监测诊断。

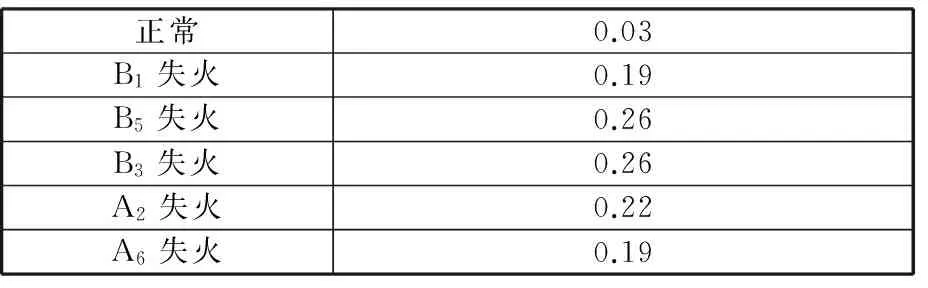
表2 各缸失火时IMF分量6中8.3 Hz成分的幅值

3.2 瞬时转速的极坐标表示及故障定位

图14是柴油机0.5谐次矢量图。该柴油机按50°/ 70°间隔角交替发火，根据分析可知，相邻发火缸的0.5谐次相位理论上会按25°/ 35°间隔交替发火，各缸之间的0.5谐次相位差唯一确定。利用这一性质，以柴油机某缸失火故障相位为基准，当其他缸发生失火故障时，可准确定位故障缸。

由上可知，IMF分量6的主频率为8.3 Hz(0.5谐次)，但其波形具有明显的幅度调制特点，直接对其进行频谱分析，求取的相位误差较大，所以本文截取柴油机一个工作循环的IMF分量6，利用极坐标表示其相位。图15是B1缸失火时瞬时转速IMF分量6的极坐标表示，以B1缸下陷区作为基准(图中箭头处)，按0.5谐次矢量图中的发火顺序和间隔角对柴油机各缸进行排列。当柴油机发生其他缸失火故障时，根据下陷区所指即可定位故障气缸。

图14 0.5谐次矢量图Fig.14 Vector of 0.5harmonic

图15 B1缸失火时瞬时转速极坐标表示 Fig.15 Polar of B1misfire IAS

为了验证极坐标表示定位故障缸的可靠性，用极坐标分别表示A2缸、A6缸、B5缸和B3缸单缸失火时柴油机一个工作循环的IMF分量6，详见图16(图中箭头所指为下陷区相位，实线直线为相邻两缸相位间隔角中间分界线，以图16a为例，当下陷区位于两条分界线之内时，判别A2缸发生故障，其他缸以此类推)。从图16可知，A2缸、A6缸和B5缸失火时，极坐标下陷区相位均位于分界线之内，故障缸定位准确；B3缸失火时，极坐标下陷区相位分布在分界线之外，故障缸不能被准确定位。

(a)A2缸失火 (b)A6缸失火

(c)B5缸失火 (d)B3缸失火图16 不同缸失火时其IMF分量6的极坐标表示 Fig.16 Polar of IMF6 misfire IAS

表3所示为各缸失火时IMF分量6的相位，从表中可以看出，A2缸、A6缸基准相位差值与理论相位差值较为接近，B3缸和B5缸基准相位差值与理论相位差值出入较大。产生这些误差的原因可能有两个方面：①V12柴油机各缸激励力矩到飞轮的传递函数并不完全一致，导致0.5谐次相位发生偏移；②B1缸失火时IMF分量6的相位本身可能存在误差，以其相位为基准，对后续失火故障定位会造成一定偏差。

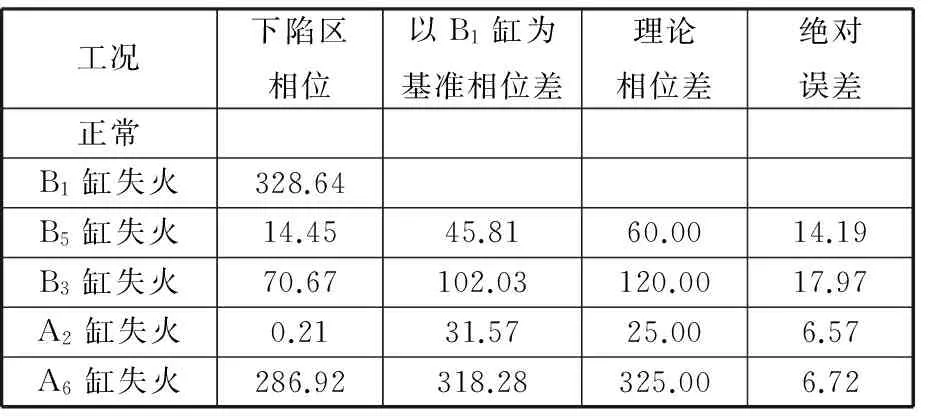
表3 各缸失火时IMF分量6中8.3 Hz成分的相位

为了进一步提高定位准确度，通过频谱分析直接计算瞬时转速的0.5谐次相位，结果如表4所示。从表4可以看出，A2缸、A6缸和B3缸基准相位差值与理论相位差值较为接近，而B5缸失火时基准相位差与理论相位差出入较大，但小于表3中的误差；并且各缸失火时的0.5谐次相位皆位于分界线之内，利用这一性质可准确定位故障缸，不发生误判。极坐标具有图形化表示的优势，它能够简单直观地给出诊断结论，但从定位角度来看，0.5谐次相位的效果更好，实际运用时可将两者联合起来进行判别，以确保定位准确。

表4 各缸失火时0.5谐次的相位

4 结论

(1)瞬时转速的HHT时频图和部分IMF分量的频谱分析结果表明，IMF分量6的主频率为8.3 Hz(0.5谐次)，经过EEMD分解，0.5谐次成分得以有效提取，它的幅值可以作为判别单缸失火故障的特征值。

(2)当柴油机按50°/ 70°间隔角交替发火，由理论分析可知，它的0.5谐次相位将以25°/ 35°曲柄转角间隔。IMF分量6包含故障缸丰富信息，将0.5谐次矢量图和其极坐标表示相结合，并辅以直接提取的0.5谐次相位，能够直观地定位故障缸。

[1] RÉMOND D，ANTONI J，RANDALL R B. Instantaneous Angular Speed (IAS) Processing and Related Angular Applications[J]. Mechanical Systems and Signal Processing，2014，45(1)：24-27.

[2] 马晋，江志农，高金吉. 基于瞬时转速波动率的内燃机故障诊断方法研究[J]. 振动与冲击，2012，31(13)：119-124. MA Jin，JIANG Zhinong，GAO Jinji. Diesel Engine Fault Diagnosis Method Based on Instantaneous Angular Speed Fluctuation Ratio[J]. Journal of Vibration and Shock，2012，31(13)：119-124.

[3] ESPADATOR F J J，VILLANUEVA J A B，GUERRERO D P. Measurement and Analysis of Instantaneous Torque and Angular Velocity Variations of a Low Speed Diesel Engine[J]. Mechanical Systems and Signal Processing，2014，49(1/2)：135-153.

[4] SCOTT X C. Model-based Engine Diagnostics and Controls Utilizing Crank Shaft Speed Measurements[D]. Madison:University of Wisconsin-Madison，1997.

[5] 华春蓉，闫兵，董大伟，等. 基于0.5谐次扭振的内燃机故障诊断研究[J]. 机械强度，2006，28(4)：480-484. HUA Chunrong，YAN Bing，DONG Dawei，et al. Study on Fault Diagnosis of Internal Combustion Engine Based on 0.5 Order Torsional Vibration[J]. Journal of Mechanical Strength，2006，28(4)：480-484.

[6] 孙云岭，朴甲哲，张永祥. Wigner-Ville时频分布在内燃机故障诊断中的应用[J]. 中国机械工程，2004，15(6)：505-507. SUN Yunling，PIAO Jiazhe，ZHANG Yongxiang. Applications of Wigner-Ville Time-frequency Distribution in Internal Combustion Engine(ICE) Fault Diagnosis[J]. China Mechanical Engineering，2004，15(6)：505-507.

[7] 刘小峰，柏林，秦树人. 基于瞬时转速的变窗STFT变换[J]. 振动与冲击，2010，29(4)：27-29. LIU Xiaofeng，BO Lin，QIN Shuren. The STFT of instantaneous Angular Speed[J]. Journal of Sound and Vibration，2010，29(4)：27-29.

[8] MATTEO M，NICOLO S. Multiple Misfire Identification by a Wavelet-based Analysis of Crankshaft Speed Fluctuation[C]// IEEE International Symposium on Signal Processing and Information Technology. Vancouver, 2006：145-148.

[9] 胡杰，颜伏伍. 基于EMD和HHT的内燃机瞬时转速信号分析[J]. 车用发动机，2010 (3)：15-19. HU Jie，YAN Fuwu. Analysis of ICE Instantaneous Speed Signal Based on EMD and HHT[J]. Vehicle Engine，2010 (3)：15-19.

[10] 高强，马志义，刘本超，等. 经验模式分解在发动机故障特征提取中的应用[J]. 长安大学学报，2010，30(3)：83-86. GAO Qiang，MA Zhiyi，LIU Benchao，et al. Application of Empirical Mode Decomposition on Engine Fault Feature Extraction[J]. Journal of Chang’an University(Natural Science Edition)，2010，30(3)：83-86.

[11] 肖小勇，向阳，钱思冲，等. 多谐次相位法在柴油机故障诊断上的应用[J]. 哈尔滨工程大学学报，2014，35(8)：954-960.

XIAO Xiaoyong，XIANG Yang，QIAN Sichong，et al. The Application of the Multi-harmonic Phase Method to Fault Diagnosis of Diesel Engines[J]. Journal of Harbin Engineering University，2014，35(8)：945-960.

[12] CHARLES P，SINHA J K，GU F，et al. Detecting the Crankshaft Torsional Vibration of Diesel Engines for Combustion Related Diagnosis[J]. Journal of Sound and Vibration，2009，321(3/5)：1171-1185.

[13] HUANG N E，SHEN Z，LONG S R，et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society London A：Mathematical Physical & Engineering Sciences，1998，454A：903-908.

[14] WU Z，HUANG N E. Ensemble Empirical Mode Decomposition：a Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis，2009，1(1):1-41.

[15] ANDRÉ H，GIRARDIN F，BOURDON A，et al. Precision of the IAS Monitoring System Based on the Elapsed Time Method in the Spectral Domain[J]. Mechanical Systems and Signal Processing，2014，44(1/2):14-30.

(编辑 王旻玥)

Fault Diagnosis Method of Instantaneous Angular Speed Based on EEMD and Polar Representation

WANG Shuai1，2XIANG Yang1，2WANG Lei1，2

1.School of Energy and Power Engineering，Wuhan University of Technology,Wuhan，430063 2.Key Laboratory of Marine Power Engineering and Technology Ministry of Communications,Wuhan，430063

In order to extract the time domain characteristic parameters and guarantee the diagnosis accuracy in high speed V-engine with high number of cylinders, the fault diagnosis method of IAS was studied by taking V12 diesel engine with unequal firing angel as object based on EEMD and polar representation. Results show that intrinsic mode function 6 (IMF6) has a main frequency component of 8.3 Hz (0.5 harmonic order). The 0.5 harmonic order components are extracted effectively by EEMD and its amplitude may be used as an characteristic value of misfire faults. The misfire cylinder may be located accurately through the combination of polar representation, 0.5 harmonic order phases and its change rules.

ensemble empirical mode decomposition(EEMD); instantaneous angular speed(IAS); single cylinder misfire; polar representation; fault location

2016-07-11

国家自然科学基金资助项目(51279148)

TK428

10.3969/j.issn.1004-132X.2017.15.013

王 帅，男，1988年生。武汉理工大学能源与动力工程学院硕士研究生。主要研究方向为内燃机故障诊断。向 阳(通信作者)，女，1962年生。武汉理工大学能源与动力工程学院教授、博士研究生导师。E-mail:yxiang@whut.edu.cn。王 磊，男，1990年生。武汉理工大学能源与动力工程学院硕士研究生。