基于加权模型参数的归一化磁源强度三维反演
饶椿锋,于 鹏,胡书凡,陈 诚
(同济大学海洋地质国家重点实验室,上海200092)
基于加权模型参数的归一化磁源强度三维反演
饶椿锋,于 鹏,胡书凡,陈 诚
(同济大学海洋地质国家重点实验室,上海200092)
强剩磁的存在使磁化方向与地磁场方向偏差很大,进而对常规的磁异常反演和解释产生很大的影响。归一化磁源强度(normalized source strength,NSS)是一种弱敏感于磁化方向的转换量,它与场源的中心对应性比同类型的转换量要好。基于模型参数加权,采用共轭梯度的反演算法,使所有反演网格单元的综合灵敏度一致,以消除NSS核函数随距离的四次方衰减的影响。将这种改进的正则化共轭梯度算法应用于剩磁条件下的NSS反演。在研究区内存在剩磁情况下,与直接反演磁异常相比,NSS反演提供了更为可靠和稳定的解;与常规正则化反演方法相比,这种模型参数加权的方式能更好地降低NSS反演中核函数随距离的四次方衰减对反演结果的影响,且其反演结果能更好地刻画场源体的几何形态与物性分布。模型和实测数据测试结果证明了该剩磁条件下的反演方法的有效性和适用性。
归一化磁源强度;加权模型参数;剩磁;三维反演;磁化率
在多数磁异常处理过程中,往往不考虑剩余磁化强度的影响。但在某些条件下,由于剩余磁化强度的存在,总场磁化强度的方向与感应磁化强度可能完全不一样。强剩磁和强磁性体的退磁作用改变了磁化强度的大小和方向,导致磁异常的幅值和形态发生畸变,影响磁测资料的反演解释[1-3]。若无总场磁化强度方向的先验信息,常规反演方法计算出来的结果都无效。如:2005年,SHEARER[4]模拟结果表明LI等[5]的反演算法在磁化方向估计误差超过15°时会产生错误的反演结果。
剩磁条件下的磁异常反演方法主要有三大类。
第一类方法:首先估计磁异常数据的磁化方向,然后直接反演总强度磁异常ΔT或垂直分量Za。1986年,唐俊德[6]提出利用磁异常三分量确定磁化方向的圆曲线法;1993年,ROEST等[7]在二维情况下,提出基于磁场总梯度模和磁源重力异常总水平梯度互相关的估计方法;1995年,MEDEIROS等[8]提出利用等效源磁矩反演估计磁化方向;2001年,甘西[9]利用磁场的垂直分量确定磁性体磁化方向;2002年,HANEY[10]在二维情况下,提出一种利用小波变换估计磁化方向的方法;2004年,BILIM等[11]通过寻找磁源重力异常与重力异常相关系数的极大值来确定磁化方向;2005年,PHILLIPS[12]给出估计磁化方向的Helbig积分法的直接算法和间接算法;2006年,NICOLOSI等[13]运用等效源算法估计地壳结构的磁化方向,同年,DANNEMILLER等[14]提出基于化极磁异常垂直梯度与总梯度模的互相关确定总磁化方向的方法;2009年,GEROVSKA等[15]通过化极磁异常与磁异常模量的互相关估计磁化方向;2010年,LI等[16]对常规的估计磁化方向方法进行对比研究,证明了这些方法不适用于磁性体磁化方向变化较大的情况;2015年,LIU等[17]在二维条件下,采用连续反演的方式获得磁性体的物性分布与磁化方向。这类方法一般适用于孤立、剩磁单一的场源体,只能估计出研究区的平均磁化方向,往往不适用于研究区磁化方向变化较大的情况。
第二类方法:将原始磁异常转化为受剩余磁化方向影响小、和场源位置对应关系较好的转换量,然后对转换量进行反演。1972年,NABIGHIAN[18]提出解析信号法(AS),研究表明二维情况下总梯度模完全独立于磁化方向;2000年,STAVREV等[19]基于磁异常模量Ta提出其它4种转换量:R模量,E模量,L模量和Q模量;并证明这些转换量在三维情况弱敏感于磁化方向,在二维情况下完全独立于磁化方向;2001年,PAINE等[20]提出两种类似于解析信号(AS)的转换量,即垂直积分的总梯度模和总梯度模的垂直积分,并将两种转换量运用于三维条带磁异常反演,取得比AS更好的反演结果;2005年,SHEARER[4]进一步提出在三维情况下弱敏感于磁化方向的转换量:磁异常模量和总梯度模,并提出直接反演这些转换量的三维反演算法;2006年,STAVREV[21]利用上述5种模量的比率来估计简单二维源的位置及形态;2010年,LI等[16]进一步补充磁异常模量反演的三维算法,并提出一套剩磁条件下的三维反演策略,将其应用于高精度航测磁数据反演并取得较好效果;2012年,BEIKI等[22]运用同样弱敏感于磁化方向的NSS数据来确定场源体的埋深;2013年,PILKINGTON等[23]反演了受多个磁化方向干扰地区的NSS数据,比直接用总场磁异常反演的结果更加可靠;2014年,LI等[24]反演了受复杂剩磁影响的磁异常模量数据。
第三类方法:直接反演磁化强度矢量。2004年,WANG等[25]首次运用反演总磁化强度矢量的三分量来获得磁化强度的方向,这种方式更适用于估计孤立、均匀磁化地质体的磁化方向;2009年,LELIVRE等[26]改进了WANG等[25]的方法,证明这种反演方法能够降低剩余磁化强度的影响。这类方法增强了反演参数的不确定性,加大了反演难度。
基于上述分析,特别是转换量NSS具有弱敏感于磁化方向的特性,本文首先介绍NSS的计算方法并与其它转换量进行了对比,然后针对磁异常反演的特点引入模型灵敏度矩阵[27],研究了基于加权模型参数的正则化共轭梯度反演算法,并应用于强剩磁条件下的NSS反演,最后利用模型和实测数据验证本文方法的有效性和适用性。
1 归一化磁源强度
归一化磁源强度(NSS)是由磁偶极子的磁异常梯度张量矩阵推导而来的转换量[28]。若一个体积为v,磁化强度分布为M的场源体产生的磁位为:
(1)
式中:|r-r0|为观测点与场源之间的距离。那么,其磁异常梯度张量Γ为:
(2)
式中:Bx,By和Bz为观测磁异常B(r)的三分量。
矩阵Γ为对称矩阵并且只含有5个独立分量,因此磁异常梯度张量矩阵Γ可以表示为:
(3)
式中:l1,l2和l3为Γ的特征向量;λ1,λ2和λ3则为其对应的特征值。WILSON[28]给出磁偶极子的归一化磁源强度μ的定义:
(4)
式中:Cm=10-7H/m;m为磁偶极矩。并且推导出NSS可由磁异常梯度张量Γ矩阵的特征值计算出来[22-23,28]:
(5)
由公式(4)可以看出,NSS与距离的四次方呈反比,与偶极子的磁矩呈正比,与磁化方向无关。NSS具有弱敏感于磁化方向的特性,当研究区域剩磁不均一时,该转换类数据相比其它剩磁处理方法更具有优势。
下面通过一个简单块体模型来说明NSS在剩磁条件下的优势。块体模型是一个中心埋深为225m,边长为250m的正方体,模型的磁化率κ为0.05,地磁场强度为50000nT,地磁场倾角为90°,地磁场偏角为0,磁化倾角为30°,磁化偏角为60°。图1a为块体模型的空间位置分布图,图1b为块体模型产生的磁异常,图1c为磁异常(图1b)转换出来的总梯度模(AS)数据,图1d为磁异常(图1b)转换出来的磁异常模量(Ta)数据,图1e为磁异常(图1b)转换出来的NSS数据。从图1c至图1e可以看出,AS,Ta,NSS都是弱敏感于磁化方向的转换量,并且NSS与场源体的中心对应性要比同类型的转换量要好。

图1 块体模型的空间位置分布(a)、块体模型产生的磁异常(b)、由磁异常转换得到的总梯度模(c)、由磁异常转换得到的磁异常模量(d)和由磁异常转换得到的归一化磁源强度(e)
2 基于加权模型参数的归一化磁源强度的正则化共轭梯度求解
由公式(4)可知:NSS随距离的四次方衰减,即NSS对深部场源信息极不敏感,所以本文引入模型灵敏度矩阵Wm[27]:
(6)
NSS正演核函数A会随着深度的增加而迅速减小(即越深的网格单元的灵敏度越小),从而导致其反演结果贴近地表而不符合实际情况。通过引入Wm模型灵敏度矩阵可消除核函数随着深度下降造成反演结果贴近地表的影响。因此,本文采用的模型参数加权为:
(7)
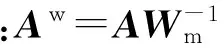
Pα(mw)=φ(mw)+αS(mw)

(8)

(9)

实测数据当中往往会含有一定量的噪声,LI等[5]提出用数据的标准偏离差的倒数作为数据加权因子并取得良好效果,本文也采用这种手段,故数据加权因子为:
(10)
式中:σi为数据的标准偏离差,若数据含噪声较少,则Wd为1。


(11)
如果(11)式成立,则表示当前的正则化因子偏大,无法使数据拟合误差明显下降,此时,按照(12)式来选取下次迭代的正则化因子。
(12)
式中:q可根据实际情况选择。
此外,我们引入PORTNIAGUINE等[29]的物性约束方式,即反演结果的物性变化范围满足mbg≤m≤mbg+mup,其中,mbg为背景物性值,mup为物性上限。
对于该正则化共轭梯度反演流程,以卡方误差作为迭代停止条件。
1) 当卡方误差达到1时,停止反演迭代,其误差的计算方式为:
(13)
式中:dcal为拟合数据;dobs为观测数据;dnoise为观测数据的标准偏离差;N为数据总个数,Erms为卡方误差。
2) 迭代次数达到最大时停止反演。
3 模型试验
理论模型由4个大小不同、物性不同、含有不同剩磁的块体组合而成,表1列出了各块体的几何参数、物性参数及磁化方向。地磁场强度为50000nT,地磁场倾角为65°,地磁场偏角为-25°。组合块体模型的空间位置分布如图2所示,模型观测磁异常数据(加入数据量级2%的高斯噪声再加1nT)如图3a所示,由磁异常换算得到的NSS如图3b所示。磁异常数据网格大小为1m×1m,反演网格剖分为1m×1m×1m,剖分网格个数为21×21×10,共4410个;地面测点在网格中心的正上方,初始模型m0=0。

表1 组合块体模型各块体的几何参数、物性参数及磁化方向
注:x1和x2表示x方向起止坐标,y1和y2表示y方向起止坐标,zt和zb表示块体的顶深和底深,I和D分别表示块体的磁化倾角和磁化偏角。
由图3b可以看出,NSS与场源体有良好的中心对应性。在强剩磁的干扰下,为了体现NSS反演比常规磁异常反演更具有优势,我们首先假设磁化方向与地磁场方向一致,利用本文提出的加权模型参数的三维反演算法对图3a所示磁总场异常进行反演。
图4a为磁异常三维反演结果,可以看出,磁异常反演结果几乎完全错误。然后,我们利用基于深度加权的正则化反演算法[5]、基于模型灵敏度的正则化反演算法[27]和本文的反演算法对图3b所示的NSS进行反演。在深度加权的正则化反演算法中,由于NSS随距离的四次方衰减,因此选取的深度加权因子衰减系数为4。为了便于比较,这3种反演方式都选取最小模型稳定器。图4b为NSS基于深度加权的正则化方法[5]反演结果,图4c为NSS基于模型灵敏度的正则化方法[27]反演结果,图4d为NSS加权模型参数反演结果。从图4中可以看出,常规反演方法的NSS反演结果比较模糊,只能大概反映出各个块体模型的位置、埋深及大致轮廓,异常体整体形态与模型基本相似,磁化率比真实值偏小;而本文提出的加权模型参数的反演结果较好,更清晰地刻画出地下场源体的几何形态与物性分布。由该模型的试验结果可知,本文的模型参数加权方式比常规的深度加权因子和模型灵敏度矩阵更能降低NSS反演中核函数随距离的四次方衰减对反演结果的影响,能更清晰地刻画出地下场源体的几何形态与物性分布。

图3 组合块体模型产生的磁异常(a)和由磁异常转换得到的NSS(b)
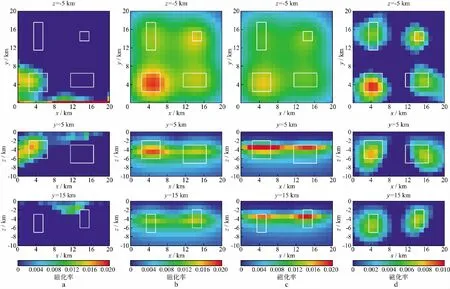
图4 磁异常反演结果(a)、NSS基于深度加权的正则化方法[5]反演结果(b)、NSS基于模型灵敏度的正则化方法[27]反演结果(c)和NSS加权模型参数反演结果(d)
4 实际资料试验
图5a为加拿大西北部地区让玛丽里弗航测磁异常,飞机飞行高度为125m。地磁场倾角为79°,地磁场偏角为21°。由图5a可以看出,图中存在两个磁化方向明显不同的局部磁异常,采用单一磁化方向对该数据进行常规磁异常反演显然不合适。因此,我们将磁异常进行换算得到NSS,如图5b所示。NSS数据与地下场源体有着良好的中心对应性。磁异常数据网格大小为0.2km×0.2km,反演网格剖分为0.2km×0.2km×0.2km,剖分网格个数为26×26×10,共6760个;地面测点在网格中心的正上方,初始模型m0=0。
我们分别采用基于深度加权的正则化反演算法和本文反演算法对图5b所示NSS进行反演,结果如图6所示。对比图6a和图6b可以看出,NSS加权模型参数的反演结果较好,能更清晰地刻画出场源体的位置、埋深、大致轮廓及物性分布。从图6可以看出,南部场源体中心埋深位于0.5km处,从0.2km延伸至1.0km;北部场源体中心埋深位于0.8km处,从0.2km延伸至1.2km;两个场源体的整体形态比较相似,北部场源体磁化率较高。这两个场源体被推断为沿着古河道展布的碎屑磁铁矿[28]。
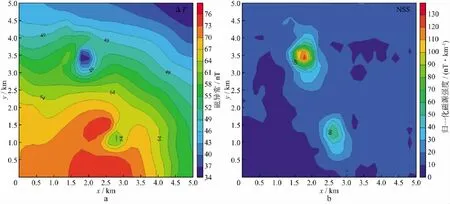
图5 加拿大西北部地区让玛丽里弗航测磁异常(a)和由磁异常转换得到的NSS数据(b)
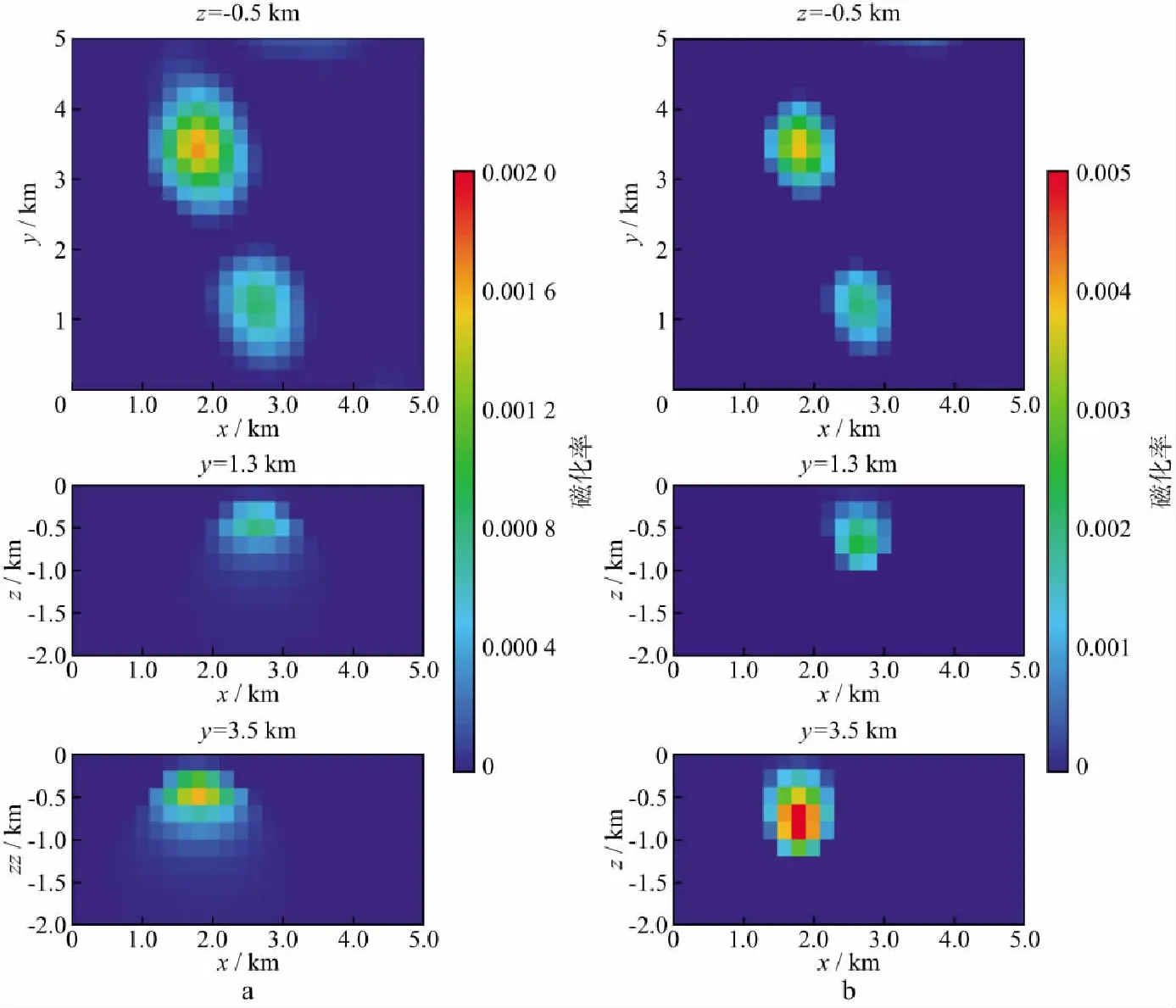
图6 图5b所示NSS基于深度加权的正则化方法[5]反演结果(a)和NSS加权模型参数反演结果(b)
5 结论
强剩磁的存在改变了磁化方向,进而影响了磁异常的反演和解释。归一化磁源强度(NSS)是一种由磁异常梯度张量换算而来的弱敏感于磁化方向的转换量,其与场源的中心对应性比同类型的转换量要好。我们将加权模型参数的正则化共轭梯度反演算法用于NSS反演。模型试验和实际资料反演证明了在强剩磁的条件下,NSS的反演结果比直接反演总场磁异常更加可靠和稳定,与常规的正则化反演方法相比,这种模型参数加权的方式能更好地降低NSS反演中核函数随距离的四次方衰减对反演结果的影响,其反演结果能更好地刻画场源体的几何形态与物性分布。在强剩磁的条件下,反演NSS数据能够基本确定场源体的位置、埋深、大致轮廓及物性分布,为磁异常的解释提供了新的思路。
[1] 李江霞,李琴,李竹强.青格里底山区块断裂与火成岩重磁异常特征研究[J].石油物探,2012,51(3):312-318 LI J X,LI Q,LI Z Q.Study on gravity & magnetic anomaly characteristics of fractures and igneous rock in Qinggelidi mountainous exploration block[J].Geophysical Prospecting for Petroleum,2012,51(3):312-318
[2] 徐世浙,张研,文百红,等.切割法在陆东地区磁异常解释中的应用[J].石油物探,2006,45(3):316-318 XU S Z,ZHANG Y,WEN B H,et al.The application of cutting method to interpretation of magnetic anomaly in region of Ludong[J].Geophysical Prospecting for Petroleum,2006,45(3):316-318
[3] 张锡林,姚长利.低磁纬度地区磁异常化极方法及应用[J].石油物探,2003,42(4):541-544 ZHANG X L,YAO C L.Reduction to the pole and its applications in area of low magnetic latitude[J].Geophysical Prospecting for Petroleum,2003,42(4):541-544
[4] SHEARER S E.Three-dimensional inversion of magnetic data in the presence of remanent magnetization[D].Colorado:Colorado School of Mines,2005
[5] LI Y,OLDENBURG D W.3-D inversion of magnetic data[J].Geophysics,1996,61(2):394-408
[6] 唐俊德.任意磁性体磁化强度方向的确定[J].桂林冶金地质学院学报,1986(2):75-81 TANG J D.Determination of the direction of magnetization for an arbitrary body[J].Journal of GuiLin College of Geology,1986(2):75-81
[7] ROEST W R,PILKINGTON M.Identifying remanent magnetization effects in magnetic data[J].Geophysics,1993,58(5):653-659
[8] MEDEIROS W E,SILVA J B C.Gravity source moment inversion:a versatile approach to characterize position and 3-D orientation of anomalous bodies[J].Geophysics,1995,60(5):1342-1353
[9] 甘西.利用微机确定磁性体磁化方向的可行性探讨[J].湖北地矿,2001,15(1):33-38 GAN X.Feasibility of the application of microcomputer method to the magnetic direction determination of the magnetic body[J].Hubei Geology & Mineral Resources,2001,15(1):33-38
[10] HANEY M.Total magnetization direction and dip from multi scale edges[J].SEG Technical Program Expanded Abstracts,2002,21(1):238-244
[11] BILIM F,ATES A.An enhanced method for estimation of body magnetization direction from pseudogravity and gravity data [J].Computers & Geosciences,2004,30(2):161-171
[12] PHILLIPS J D.Can we estimate total magnetization directions from aeromagnetic data using Helbig’s integrals[J].Earth Planets & Space,2005,57(8):681-689
[13] NICOLOSI I,BLANCO-MONTENEGRO I,PIGNATELLI A,et al.Estimating the magnetization direction of crustal structures by means of an equivalent source algorithm[J].Physics of the Earth & Planetary Interiors,2006,155(1/2):163-169
[14] DANNEMILLER N,LI Y.A new method for determination of magnetization direction[J].Geophysics,2006,71(6):L69-L73
[16] LI Y G,SHEARER S E,HANEY M M,et al.Comprehensive approaches to 3D inversion of magnetic data affected by remanent magnetization[J].Geophysics,2010,75(1):L1-L11
[17] LIU S,HU X,XI Y,et al.2D sequential inversion of total magnitude and total magnetic anomaly data affected by remanent magnetization[J].Geophysics,2015,80(3):K1-K12
[18] NABIGHIAN M N.The analytic signal of two-dimensional magnetic bodies with polygonal cross-section its properties and use for automated anomaly interpretation[J].Geophysics,1972,37(3):507-517
[19] STAVREV P,GEROVSKA D.Magnetic field transforms with low sensitivity to the direction of source magnetization and high centricity[J].Geophysical Prospecting,2000,48(2):317-340
[20] PAINE J,HAEDERLE M,FLIS M.Using transformed TMI data to invert for remanently magnetised bodies[J].Exploration Geophysics,2001,32(4):238-242
[21] STAVREV P.Inversion of elongated magnetic anomalies using magnitude transforms[J].Geophysical Prospecting,2006,54(2):153-166
[22] BEIKI M,CLARK D A,AUSTIN J R,et al.Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J].Geophysics,2012,77(6):J23-J37
[23] PILKINGTON M,BEIKI M.Mitigating remanent magnetization effects in magnetic data using the normalized source strength[J].Geophysics,2013,78(3):J25-J32
[24] LI S L,LI Y G.Inversion of magnetic anomaly on rugged observation surface in the presence of strong remanent magnetization[J].Geophysics,2014,79(2):J11-J19
[25] WANG M Y,DI Q Y,KUN X U,et al.magnetization vector inversion equations and forword and inversed 2-d model study[J].Chinese Journal of Geophysics,2004,47(3):601-609
[27] ZHDANOV M S.Geophysical inverse theory and regularization problems[M].The Netherlands:Elsevier Science,2002:1-50
[28] WILSON H S.Analysis of the magnetic gradient tensor[R].Canada:Defence Research Establishment Pacific,Technical Memorandum,1985:5-13
[29] PORTNIAGUINE O,ZHDANOV M S.Focusing geophysical inversion images[J].Geophysics,1999,64(3):874-887
(编辑:顾石庆)
The 3D inversion of the normalized source strength data based on weighted model parameters
RAO Chunfeng,YU Peng,HU Shufan,CHEN Cheng
(StateKeyLaboratoryofMarineGeology,TongjiUniversity,Shanghai200092,China)
The existence of strong remanent magnetization makes the large deviation between the total magnetization direction and the induced magnetization direction.Moreover it will have a great impact on the conventional magnetic anomaly inversion and interpretation.The normalized source strength (NSS) is a quantity which minimally affected by the direction of remanent magnetization.The NSS produces a higher level of centricity compared to the other transformations of the magnetic field that are used for the same purpose.In this paper,we use a conjugate gradient inversion algorithm based on weighted model parameters to make all inversion grid cells have the same integrated sensitivity,which can be used to eliminate the effects caused by the NSS forward operator decay with fourth power of distance.Under the effects of strong remanent magnetization,we applied the improved regularization conjugate gradient algorithm to invert the NSS data.The NSS inversion produces a more reliable and stable image of the subsurface magnetization distribution than using the observed magnetic field data directly.What’s more,compared with conventional 3D inversion,the weighted model parameters can better reduce the effects from the decay with fourth power of distance and the NSS inversion results can better depict the geometry and physical properties distribution of the source body.We verify the effectiveness and applicability of the inversion method presented in this paper for three dimensional magnetic susceptibility with synthetic and field data.
the normalized source strength,weighted model parameters,remanent magnetization,3D inversion,magnetic susceptibility
2016-05-05;改回日期:2017-02-15。
饶椿锋(1993—),男,硕士在读,主要研究方向为重磁电反演。
于鹏(1969—),男,教授,博士生导师,理学博士,主要研究方向为综合地球物理正反演。
国家科技重大专项(2016ZX05004-003,2016ZX05027-001-008)、国家重点研发计划深地专项项目(2016YFC0601104)、国家自然科学基金(41506053)和海洋地质国家重点实验室自主课题(MG20170204)共同资助。
P631
A
1000-1441(2017)04-0599-08
10.3969/j.issn.1000-1441.2017.04.017
This research is financially supported by the National Science & Technology Major Project of China (Grant Nos.2016ZX05004-003,2016ZX05027-001-008),the National Key Research & Development Program of China (Grant No.2016YFC0601104),the National Natural Science Foundation of China (Grant No.41506053),the State Key Laboratory of Marine Geology (Grant No.MG20170204).

