双耦合振动Matlab分析研究

董 刚

(楚雄师范学院物理与电子科学学院，云南 楚雄 675000)

双耦合振动Matlab分析研究

董 刚

(楚雄师范学院物理与电子科学学院，云南 楚雄 675000)

本文以理论力学中双耦合振动为例，以Matlab科学计算软件为开发平台，分析研究双耦合振动演示的开发过程。并与国外用Java技术开发的双耦合振动演示进行比较。培养学生创新思维能力。

双耦合振动；Matlab；振动演示

1.引言

力学系统多数为复杂的非线性系统，不可能对其运动得出一般解。作为求解的试探，常常是对相对于平衡位置有微小偏离的运动求解。利用保守力系拉格朗日方程，求出耦合振动在平衡位置附近作小振动时的本证频率，并对耦合振动坐标作适当的线性组合[1]，观察耦合振动的情况。多振子耦合振动的显著特点是振子之间发生能量传递，能量传递的发生是由于相邻两振子的物理参量之间具有耦合作用[2]。耦合振动由于其复杂性，耦合摆的小振动在理论力学中曾求解过,但求解过程繁琐[3]，很难给出形象直观的振动图像。国外使用Java技术开发的耦合振动演示课件GeneralPhysicsAnimations[4]。耦合振动演示，形象直观，引人思考，但没有耦合振动的分析过程，开发说明，无从知晓课件的开发过程。而物理课件的开发过程包含深奥的物理过程和复杂的计算机技术。本文以理论力学中双耦合振动为例，以Matlab科学计算软件为开发平台，分析研究双耦合振动的开发过程，并与国外用Java技术开发的双耦合振动结果进行比较。

2.双耦合振动

如图1所示，为国外使用Java技术开发的双耦合振动，形象给出两个振动质点的振动过程和振动图像，弹簧的参数通过滚动条调节，演示方便，形象直观。但双耦合振动包含的物理过程，课件制作的过程很难知晓。以下通过双耦合振动物理过程分析，Matlab程序设计，双耦合振动过程演示，再现双耦合振动物理课件制作开发过程。

图1 使用Java技术开发的双耦合振动

3.双耦合振动过程分析

图2 两质点三弹簧构成的双耦合振动系统

3.1双耦合振动系统

耦合振动在工程技术、分子振动等领域有重要应用。两个质点，放在光滑的平面上，两个质点，三个弹簧构成双耦合振动系统。图2为两质点三弹簧构成的双耦合振动系统。

3.2双耦合振动物理过程分析

N个自由度的系统，可由N个独立变量描述其运动，每个独立变量的谐振动频率称为振动系统特征振动频率，当系统以特征频率振动时，它各部分的具体振动方式就是系统的振动模式。双耦合振动是两套振动系统相互耦合，振动具有不同振动模式，不同的特征振动频率。系统有2个自由度，取x1，x2为广义坐标，

系统的势能为：V=kx12+kx22-kx1x2

令x1=A1cos(ωt+φ)，x2=A2cos(ωt+φ)代入(1)(2)式得：

两振幅有非零解的条件是系数行列式为零，

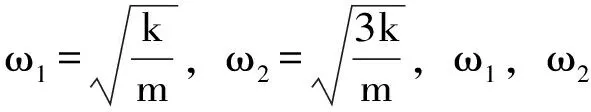
将ω1代入(3)，(4)得A1=A2两物体做同相振动

将ω2代入(3)，(4)得A1=-A2两物体做反相振动

一般振动为两个简谐振动的线性叠加

x1=A1cos(ω1t+φ1)+A2cos(ω1t+φ1)

x2=A1cos(ω1t+φ1)-A2cos(ω1t+φ1)

3.3 耦合振动的振动模式

(1)同相振动，当ω=ω1时，即频率较小时，两物体作同相等频率振动。

(2)反相振动，当ω=ω2时，即频率较大时，两物体作反相等频率振动。

(3)一般情况，两物体振动为上述两种情况的线性叠加。

图3 弹簧参数不同的双耦合振动系统

3.4 改变耦合振动参数

如图3所示，通过理论计算

两物体振动情况与上述分析相同，即频率较小时，两物体作同相等频率振动，频率较大时，两物体作反相等频率振动，一般情况，两物体振动为上述两种情况的线性叠加。

4.双耦合振动程序设计

4.1程序设计说明

Matlab是大学较为流行的科学计算软件，具有语言简单，函数库丰富，图形化功能强的特点。根据上述理论分析，通过Matlab程序设计，计算出系统的特征频率。取m=240，k=48，语句[V,D]=eig(M)，其中V为本征矢，D为本征值，w=sqrt(D)即为本征频率。计算出本征频率为：ω1=0.3162，ω2=0.5477，设置三种不同的初始条件，设两物体的初速度为零，初相为零，给出三种典型的振动模式

第一种情况：x10=x20>0，同相振动

x1=x10cos ω1t

x2=x20cos ω1t

第二种情况：x10<0，x20=-x10，反相振动

x1=x20cos (ω2t+π)

x2=x20cos ω2t

第三种情况：x10>0，x20=0，耦合振动的一般振动

4.2程序设计主要代码

clearall

m=240;

k1=48;

k2=120

M=[(2*k1+k2)/m,-k/m;-k/m,(2*k1+k2)/m];

[V,D]=eig(M)

w=sqrt(D)

A1=[0.1;0;0.10];

A2=[0;-0.1;0.10];

phi1=0;phi2=0;

t=0:0.04:150;

forj=1:3

figure(j+1)

x1=A1(j)*cos(w(1,1)*t+phi1)+A2(j)*cos(w(2,2)*t+phi2);

x2=A1(j)*cos(w(1,1)*t+phi1)-A2(j)*cos(w(2,2)*t+phi2);

subplot(2,1,1)

axis([0 20 -0.3 0.3])

plot(t,x1)

gridon

xlabel(’t/s’)

ylabel(’x1/m’)

subplot(2,1,2)

axis([0 20 -0.3 0.3])

plot(t,x2)

gridon

xlabel(’t/s’)

ylabel(’x2/m’)

end

5.双耦合振动的振动演示

5.1m1=m2=240,k1=k2=48时，双耦合振动演示

图4、图5、图6分别给出了小频率的同相振动、大频率的反相振动、一般情况线性叠加的双耦合振动演示图。

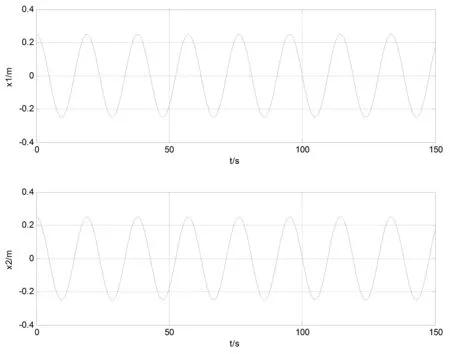
图4 小频率的同相振动

图5 大频率的反相振动

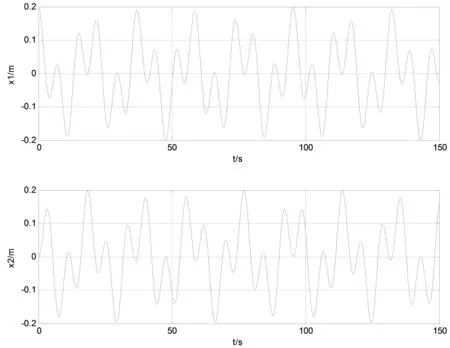
图6 一般情况的线性叠加

图7 小频率的同相振动

从图6可见一般情况的线性叠加，与Java课件振动图像相似。

5.2m1=m2=240,k1=24，k2=120时，双耦合振动演示

图7、图8、图9分别给出了小频率的同相振动、大频率的反相振动、一般情况线性叠加的双耦合振动演示图。

从图9可以看出，双耦合振动的振动与Java课件振动情况完全相同，与Java课件只能演示两物体一般情况振动线性叠加的情况，双耦合振动Matlab交互式课件与Java课件比较，演示内容更丰富，参数调节更方便。

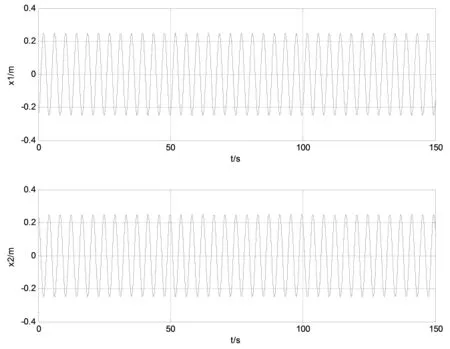
图8 大频率的反相振动

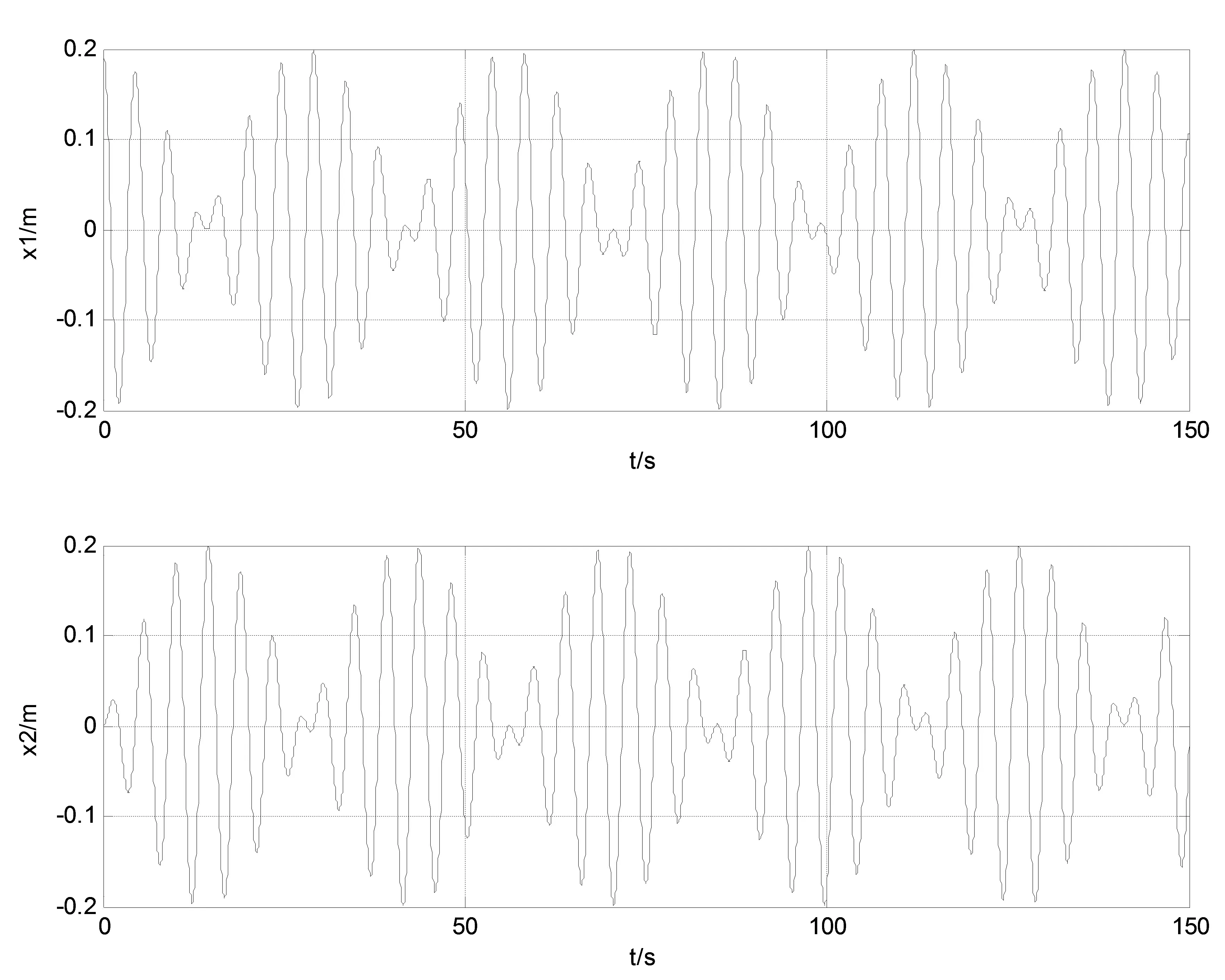
图9 一般情况的线性叠加

6.结论

通过双耦合振动交互式物理课件Matlab程序设计，与Java演示课件比较发现，物理课件的开发过程并非易事，涉及深奥物理知识和复杂的计算机技术，涉及教学理念的更新，开发平台的选择，涉及物理过程的分析和结果的讨论，通过双耦合振动Matlab分析研究可以得出以下结论：

(1)Matlab演示结果与Java演示结果完全相同；

(2)演示内容丰富，参数调节方便；

(3)培养分析问题，解决问题，创新思维能力；

(4)用同样的分析方法，也可以研究三耦合的振动情况。

[1]韩萍.耦合振动小振动问题研究[J].辽宁工业大学学报，2008,28(2):138―140.

[2]师一华.多振子耦合振动分析与研究[J].郑州轻工业学院学报，2000,15(1):78―80.

[3]吴清林，杨文明.对串联耦合振动的模拟与研究[A].物理与工程.全国高等学校物理基础课程教育学术研讨会论文集[C].2013:154―157.

[4]Java课件演示网址：http://www.surendranath.org/

(责任编辑 司民真)

AnAnalyticalStudyofDoubleCoupledOscillationswithMatlab

DONGGang

(School of Physics & Electronic Science, Chuxiong Normal University, 675000, Yunnan Province)

Inthispaper,thedoublecoupledoscillationsintheoreticalmechanicsistakenasanexample.WithMatlabscientificcomputingsoftwareasthedevelopmentplatform,thethesisanalyzesthedevelopmentprocessofdoublecoupledoscillations.ComparedwiththedoublecoupledoscillationsdevelopedbyJavatechnologyabroad,thestudyaimsattrainingstudents’creativethinkingability.

DoubleCoupledoscillations；Matlab；Vibrationdemonstration

教育部高等学校大学物理课程教学指导委员会教学改革项目，项目编号：DWJZW201540xn。

2017 - 04 - 16

董 刚(1963―)，男，楚雄师范学院物理与电子科学学院教授，研究方向：物理学，物理课件制作。

O

A

1671 - 7406(2017)03 - 0013 - 05