Magnetpolaron effect in two-dimensional anisotropic parabolic quantum dot in a perpendicular magnetic field∗

Kang-Kang Ju(居康康),CuiXian Guo(郭翠仙),and Xiao-Yin Pan(潘孝胤)

Department of Physics,Ningbo University,Ningbo 315211,China

Magnetpolaron effect in two-dimensional anisotropic parabolic quantum dot in a perpendicular magnetic field∗

Kang-Kang Ju(居康康),CuiXian Guo(郭翠仙),and Xiao-Yin Pan(潘孝胤)†

Department of Physics,Ningbo University,Ningbo 315211,China

We study the two-dimensional weak-coupling Fröhlich polaron in a completely anisotropic quantum dot in a perpendicular magnetic field.By performing a unitary transformation,we first transform the Hamiltonian into a new one which describes an anisotropic harmonic oscillator with new mass and trapping frequencies interacting with the same phonon bath but with different interaction form and strength.Then employing the second-order Rayleigh–Schrödinger perturbation theory,we obtain the polaron correction to the ground-state energy.The magnetic field and anisotropic effects on the polaron correction to the ground-state energy are discussed.

Fröhlich polaron,anisotropic quantum dot,magnetic field,ground-state energy

1.Introduction

During the past few decades,tremendous experimental and theoretical interest in low-dimensional systems has been stimulated by the technological advances in the fabrication of nanostructures,[1–4]we refer the readers to Ref.[4]for the latest developments.Nowadays it is possible to confine a few electrons in all three spatial dimensions in semiconductors called quantum dots(QDs).[5–9]This confinement feature brings in quantum effects,for example,the electron energy spectrum of such quantum dots is fully quantized.Because of their potential applications in designing devices and lots of interesting new quantum physical effects arising from their nanometer length scales,understanding the electronic properties of QDs is of particular importance.

The electron–phonon interaction,which plays an impor-tantrole in electronic and optical properties of polar crystalline materials in three dimensions,also has pronounced effects in low-dimensional systems.Numerous investigations have been devoted to the electron–phonon interaction,especially the interaction of the electrons with longitudinal-optical(LO) phonons,on various electronic properties of semiconductor QD.[10–15]Among these,many authors calculated the ground state energies using different methods such as the second-order perturbation theory,[11]the Feynman–Haken variational pathintegral method,[12]the Lee–Low–Pines–Huybrecht(LLP-H) method,[13]and Landau–Pekar(LP)variational theory.[15]The general consensus they reached is that the polaronic correction becomes considerably stronger as the strength of the dot confi ning potential increases,and the polaronic effects are very significant.

In the presence of an external magnetic field,the polaron effects in QDs become more interesting,because the magnetic field will affect the confinement length.There exist a considerable amount of studies devoted to this subject in the literature.For instance,Haupt and Wendler[16]investigated the cyclotron resonance of magnetopolarons in three dimensional completely anisotropic parabolic QDs,analytical and numerical results were presented for the anisotropy and polaron corrections to the Landau levels of an isotropic parabolic QD.They also studied[17]the electronic ground state properties of the polaron in an array of anisotropic parabolic QDs in the presence of a quantizing magnetic field.Within the framework of the Rayleigh–Schrödinger perturbation theory(RSPT),[18]Zhu and Gu[19]investigated the cyclotron resonance of a magnetopolaron in a QD with a strong magnetic field.Yip[20]also studied the similar problem using an operator method.Zhu and Kobayashi[21]calculated the binding energy of strong-coupling polarons in QDs using the LP variational method.They also investigated the resonant shallow donor magnetopolaron effect[22]and the temperature dependence of magnetopolaron[23]in a GaAs/AIGaAs QD in a magnetic field.Kandemir and Altanhan[24,25]studied the polaronic effects for an electron confined in a three dimensional parabolic QD and a uniform magnetic field using the Lee–Low–Pines(LLP)method.Recently,Chen studied the cyclotron resonance of impurity magnetopolarons in two-dimensional QDs[26]and the magnetic field effects on the properties of the GaAs QD qubit due to electron–phonon interactions.[27]

Of course,the above mentioned works are not a completelist.However,it must be pointed out that in almost all the above mentioned works,as long as they are based on some analytical wave functions,the systems they considered though were referred to as trapped by“anisotropic harmonic potentials”and in a perpendicular magnetic field,they are actually planar isotropically trapped(ωx=ωy),i.e.,the anisotropies have been introduced along the z axis of the confinement rather than laterally in the 3D case.Because all the different methods used are based on the fact that the wave functions for the circular parabolic confinement trapped systems in a perpendicular magnetic field,the so called Fock–Darwin states,[28]can be manipulated analytically with less difficulty,while in the (ωxωy)or elliptic parabolic confinement,the wave functions become very complicated[29]and almost analytically intractable.To the best of our knowledge,reference[16]is probably the only work where the polaron effects of the QDs with the elliptic parabolic confinement in a perpendicular magnetic field are considered.However,for the above reason,the authors used the isotropic part of the Hamiltonian as the unperturbed one to avoid the difficulty.Hence,somehow the polaron effects in the QDs with elliptic parabolic confinement under a perpendicular magnetic field have become a long standing problem.

In contrast,there exist quite a lot of studies for the anisotropic QDs where the broken rotational symmetry brings in lots of new physics,especially the effects of anisotropy.[30–42]For instance,the shell structure pattern in the addition energy spectra is much less pronounced for small deformations and vanishes for stronger anisotropies.[31]The degeneracy in the single-particle excitation spectrum is lifted due to the reduction of the symmetry and the selection rules are affected by producing coupling effects between the states.[32]On the other hand,the magnetic field dependence properties such as magnetization for anisotropic QDs have also been studied.[38]

Thus,it is desirable to investigate the polaron effects in the QDs with elliptic parabolic confinement in the presence of a perpendicular magnetic field.In this paper,we study a two-dimensional(2D)system trapped by an anisotropic harmonic potential(ωxωy)in a perpendicular magnetic field. To overcome the long standing difficulty,instead of working directly with the complicated wave functions,we first perform a unitary transformation and convert the Hamiltonian into a new one which describes a harmonic oscillator(HO) with new masses and trapping frequencies interacting with the same phonon bath but with different interaction form and strength.This unitary transformation method is equivalent to working with the original Hamiltonian in the basis consisting of the complicated wave functions.Then the second-order Rayleigh–Schrödinger perturbation theory(RSPT)is employed to obtain the polaron correction to the ground-state energy,the magnetic field dependence and anisotropy of the polaron effects are demonstrated,the validity of the results is also discussed.

The rest of the paper is organized as follows.In Section 2,we perform the unitary transformation and obtain the new Hamiltonian,then we give the polaron correction to the ground-state energy using the second-order RSPT.The numerical results for the magnetic field and anisotropic effects are presented in Section 3.Finally,a brief conclusion is drawn in the last section.

2.Formulation

Consider an electron with an effective mass m∗confined in a 2D anisotropic QD,i.e.,the confining potential is[37,38]

One may rewrite ωx=ω0sin(φ)and ωy=ω0cos(φ),the degree of anisotropy is reflected by the angle φ,the case of φ=π/4 corresponds to the circular parabolic confinementand the confinement becomes wirelike when φ→π/2.Note that the 2D quantum dot maybe experimentally realized in a 3D system where the electrons are much more strongly confined in one direction(taken as the z direction)than in the other two directions.[5,8]

In the presence of a magnetic field B along the z direction, the Fröhlich Hamiltonian of the electron–phonon system can be written as

Here the unperturbed Hamiltonian is

where

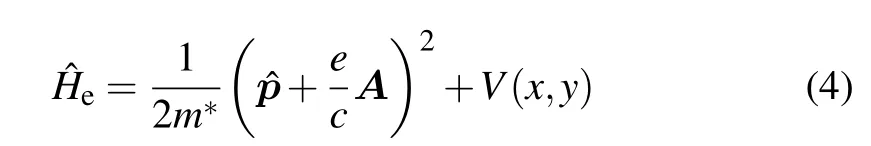
is the Hamiltonian of the electron,ωLOis the LO phonon frequency,and

describes the interaction between the electron and phonons, withcreating a bulk LO phonon of wave vector q.Vqis defined as

where q=|q|,α is the electron–phonon coupling constant, and A is the area of the sample.Note that Vqdepends only on the length of q.

Without loss of generality,we assume ωx≥ωy.Then working in the symmetric gaugeperforming the unitary transformation[29]

with

we obtain a new Hamiltonian

where the transformed unperturbed part of the Hamiltonian is

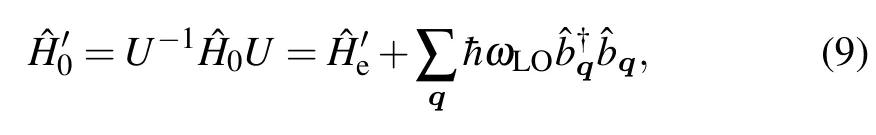
with the transformed electronic Hamiltonian

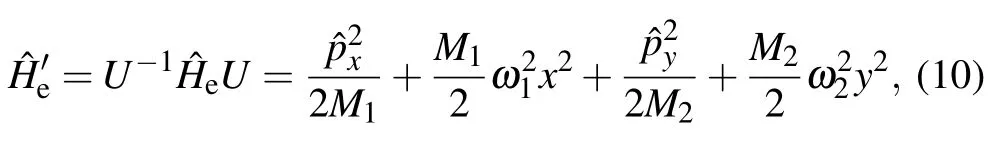
which describes a 2D HO with an anisotropic mass

and frequency

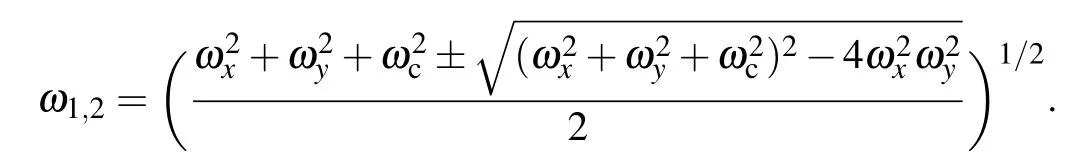
The transformed interaction part of the Hamiltonian is

Next we shall focus on the transformed Hamiltonianand use the second-order RSPT to obtain the electronic ground-state energy shift,which is given by

where|j〉=|j1j2〉is the j-th eigenstate of the transformed electronic Hamiltonian,i.e.,in the coordinate-representation, we have

This is nothing else but a simple 2D harmonic oscillator,and we readily obtain

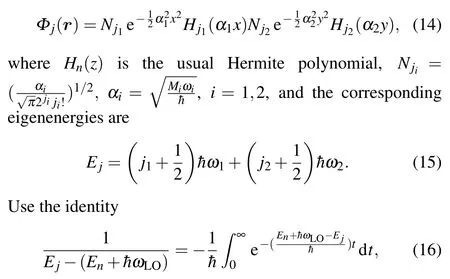
with the time-dependent coefficients

Substituting Eqs.(14)and(18)into Eq.(17),after long algebra manipulations,we finally obtain

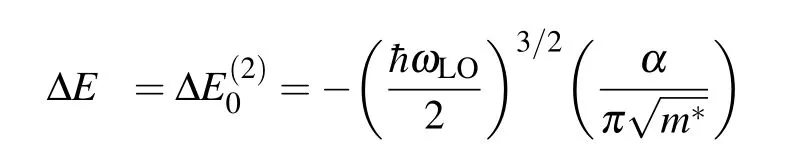
Equation(19)is the key result of this paper.Unfortunately, the integral cannot be calculated analytically.Note that for an isotropic 2D QD in a magnetic field(ωx=ωy=ω0),equation(19)reduces to

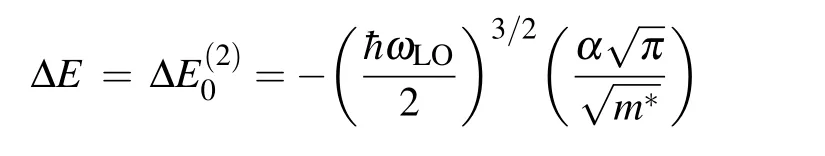
3.Numerical results and discussion

To further analyze the results obtained,we perform numerical calculations for Eqs.(19)and(20).In the following, we use the Feynman units,i.e.,m∗=¯h=ωLO=1.In the following graphs,we set φ=π/4,2π/5,9π/20,(π−δ)/2,with δ=10−3.

Fig.1.(color online)The magnitudes of the polaron correction to the ground-state energy over the coupling constant α,−ΔE/α,as a function of the cyclotron frequency ωc for different degrees of anisotropy.We set ωx=ω0 sin(φ),ωy=ω0 cos(φ),ω0=5.0,10.0,15.0,20.0,25.0, 30.0,and φ=π/4,2π/5,9π/20,(π−δ)/2,with δ=10−3.

In Fig.1,we plot the magnitude of the polaron correction to the ground-state energy over the coupling constant,α−ΔE/α,as a function of the cyclotron frequency ωcwhen ω0=5.0,10.0,15.0,20.0,25.0,30.0.From the graphs,we can see that the electron–LO phonon interaction produces a negative shift to the ground-state energy,namely,the polaron correction is negative,and the magnitude increases as the strength of the magnetic field increases for fixed coupling constant α. As the degree of anisotropy increases,i.e.,as φ increases from π/4 to π/2,the magnitude decreases,while the correction increases since it is negative.

In Figs.2 and 3,we plot the ground-state energies without and with the polaron effects,namely,E0and E=E0+ΔE,as a function of the cyclotron frequency ωcfor different degrees of anisotropy.It is clear that E0and E always increase as the strength of the magnetic field increases,while the anisotropy always lowers the ground-state energies no matter whether the polaron effects are taken into account or not,and the stronger the anisotropy is,the lower the energy becomes.

Fig.2.(color online)The ground-state energies without and with the polaron effects,namely,E0 and E=E0+ΔE,as a function of the cyclotron frequency ωc for different degrees of anisotropy.We set ωx=ω0 sin(φ),ωy=ω0 cos(φ),and ω0=5.0,10.0,15.0;φ=π/4,2π/5, 9π/20,(π−δ)/2,with δ=10−3.

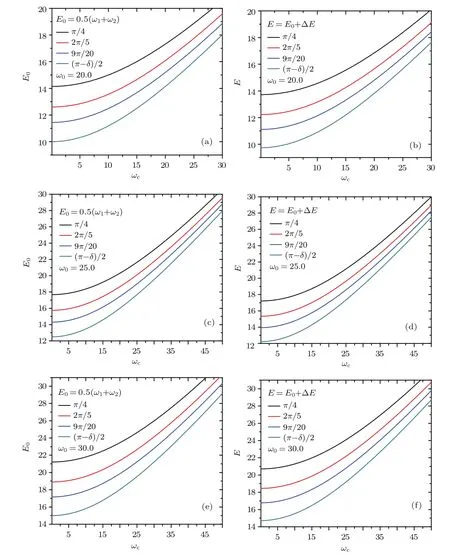
Fig.3.(color online)The same as Fig.3,but with ω0=20.0,25.0,30.0.

In order to check the validity of the RSPT,we also plot the ratios of the correction to the ground-state energy without the polaron effects,i.e.,|ΔE/E0|,as functions of ωcin Fig.4. It is clear that all the ratios are less than 10%and the values decrease as ωcincreases,thus the applicability of RSPT is justified if we set the criteria for validity to be that the correction shall not be greater than 10%of the unperturbed ground-state energy.It should be pointed out that when the value of ω0becomes smaller,say ω0＜5.0,then|ΔE/E0|increases and could be greater than 10%,then the applicability of RSPT becomes questionable.On the other hand,we note that at different values ofω0,the curves of the ratio behave quite differently for different degrees of anisotropy as shown in the graphs.It is apparent that at ω0=5.0,the ratio increases as the degree of anisotropy increases and the situation becomes opposite at ω0=30.0.The details of the evolution of this change in between are shown for ω0=10.0,15.0,20.0,25.0.

Fig.4.(color online)The magnitudes of polaron correction to the ground-state energy over the ground-state energy−ΔE/E0 as a function of the cyclotron frequency ωc for different degrees of anisotropy.We set ωx=ω0 sin(φ),ωy=ω0 cos(φ),ω0=5.0,10.0,15.0,20.0,25.0,30.0, and φ=π/4,2π/5,9π/20,(π−δ)/2,with δ=10−3.

4.Conclusion

We have investigated the system of a 2D weak-coupling Fröhlich polaron in an anisotropic quantum dot in a perpendicular magnetic field.To avoid directly using the wave function for the electronic part of the Hamiltonian which is almost analytically intractable,we transformed the total Hamiltonian into a new one by performing a unitary transform.The new Hamiltonian describes a 2D harmonic oscillator with a new mass and trapping frequencies interacting with the same phonon bath but with different interaction form and strength.We then calculated the polaron correction to the ground-state energy by using the second-order RSPT,it is found that the magnetic field will produce a negative shift to the ground-state energy, and this shift increases as the strength of the magnetic field increases.Moreover,in the valid domain of the perturbation theory,it is shown that as the degree of anisotropy increases, the ground state energy decreases.However,the ratio of correction is not necessarily the case.In fact,it depends upon the confining frequencyand could behave quite differently.This is expected to be confirmed by experiments.

Finally,it is worth stressing that although the problem we considered is 2D,the unitary transformation method can be generalized to the 3D case.Furthermore,various other methods such as the LP or LLP-H variational method and path integral approach can be applied to study the same problem. These are our future works and will be presented elsewhere.

[1]Kastner M A 1992 Rev.Mod.Phys.64 849

[2]Zimbovskaya N A and Pederson M R 2011 Phys.Rept.509 1

[3]Zhou L L 2011 Chin.Phys.Lett.28 128504

[4]Harrison P and Valavanis A 2016 Quantum Wells,Wires and Dots:Theoretical and Computational Physics of semiconductor nanostructures (4th Edn)(Chichester:John Wiley and Sons Ltd)

[5]Sikorski C and Merkt U 1989 Phys.Rev.Lett.62 2164

[6]Reimann S M and Manninen M 2002 Rev.Mod.Phys.74 1283

[7]Chakraborty T 1999 Quantum Dots(Amsterdam:Elsevier)

[8]Ferreyra J M,Bosshard P and Proetto C R 1997 Phys.Rev.B 55 13682

[9]Hanson R,Kouwenhoven L P,Petta J R,Tarucha S and Vandersypen L M K 2007 Rev.Mod.Phys.79 1217

[10]Degani M H and Farias G A 1990 Phys.Rev.B 42 11950

[11]Zhu K D and Gu S W 1992 Phys.Lett.A 163 435

[12]Chen Q,Ren Y,Jiao Z and Wang K 1998 Phys.Rev.B 58 16340

[13]Kervan N,Altanhan T and Chatterjee A 2003 Phys.Lett.A 315 280

[14]Yan Z W and Feng Z Y 2016 Chin.Phys.B 25 107804

[15]Yao Q Z and Chen S H 2011 J.Low.Temp.Phys.162 34

[16]Haupt R and Wendler L 1993 Physica B 184 394

[17]Haupt R and Wendler L 1994 Solid-State Electron.37 1153

[18]Mitra T K,Chatterjee A andMukhopadhyay S S 1987 Phys.Rept.153 91

[19]Zhu K D and Gu S W 1993 Phys.Rev.B 47 12941

[20]Yip S K 1989 Phys.Rev.B 40 3682

[21]Zhu K D and Kobayashi T 1994 Phys.Lett.A 190 337

[22]Zhu K D and Kobayashi T 1994 Sol.Stat.Commun.92 353

[23]Zhu K D and Kobayashi T 1995 Sol.Stat.Commun.95 805

[24]Kandemir B S and Altanhan T 1999 Phys.Rev.B 60 4834

[25]Kandemir B S and Altanhan T 1999 Phys.Lett.A 287 403

[26]Chen S H 2011 Physica E 43 1007

[27]Chen S H 2014 Physica B 452 55

[28]Fock V 1928 Z.Phys.47 446

[29]DippelO,SchmelcherP and Cederbaum L S 1994 Phys.Rev.A 49 4415

[30]Ezaki T,Mori N and Hamaguchi C 1997 Phys.Rev.B 56 6428

[31]Maksym P A 1998 Physica B 249 233

[32]Ezaki T,Mori N and Hamaguchi C 1998 Physica B 249 238

[33]Reimann S M,Koskinen M,Lindelof P E and Manninen M 1998 Physica E 2 648

[34]Reimann S M,Koskinen M,Kolehmainen J,Manninen M,Austing D G and Tarucha S 1999 Eur.Phys.J.D 9 105

[35]Austing D G 1999 Phys.Rev.B 60 11514

[36]Lee I H,Kim Y H and Ahn K H 2001 J.Phys.:Condens.Matter 13 1987

[37]Drouvelis P S,Schmelcher P and Diakonos F K 2004 Phys.Rev.B 69 035333

[38]Drouvelis P S,Schmelcher P and Diakonos F K 2004 J.Phys.:Condens.Matter 16 3633

[39]Ko´sik P and Okopińska A 2010 Phys.Lett.A 374 3841

[40]Yannouleas C and Landman U 2007 Rep.Prog.Phys.70 2067

[41]Birman J L,Nazmitdinov R G and Yukalov V I 2013 Phys.Rep.526 1

[42]Kokiantonis N and Castrigiano D P L 1987 J.Phys.A:Math.Gen.18 45

[43]Yonei K 1989 J.Phys.A:Math.Gen.22 2415

3 May 2017;revised manuscript

6 June 2017;published online 18 July 2017)

10.1088/1674-1056/26/9/097103

∗Project supported by the National Natural Science Foundation of China(Grant No.11375090)and the K.C.Wong Magna Foundation in Ningbo University, China.

†Corresponding author.E-mail:panxiaoyin@nbu.edu.cn

©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn