温度变化对悬索主共振响应影响分析
赵珧冰, 彭 剑
(1. 华侨大学 土木工程学院, 福建 厦门 361021; 2. 湖南科技大学 土木工程学院, 湖南 湘潭 411201;3. 湖南大学 土木工程学院, 长沙 410082)
温度变化对悬索主共振响应影响分析
赵珧冰1, 彭 剑2, 3
(1. 华侨大学 土木工程学院, 福建 厦门 361021; 2. 湖南科技大学 土木工程学院, 湖南 湘潭 411201;3. 湖南大学 土木工程学院, 长沙 410082)
基于增量热场理论,推导考虑均匀温度变化影响下受谐波激励的悬索非线性运动微分方程,利用Galerkin法将方程离散,并对离散后的方程进行线性分析。以悬索主共振响应为例,利用多尺度法求解其高阶近似解及幅频响应方程,通过算例研究温度变化对不同Irvine参数的悬索前四阶模态频率以及幅频响应曲线的影响。研究结果表明:悬索模态振型、频率和主共振响应受温度变化影响明显,且与其Irvine参数密切相关;温度变化有可能定性和定量地改变悬索非线性振动特性,其取决于线性项、平方和立方非线性项系数受温度变化的影响程度;相同程度的升温和降温对悬索振动特性的影响不对称。
悬索; 温度变化; 多尺度法; 主共振
索结构是大跨度斜拉桥以及悬索桥重要的基本单元,在实际工程中,由于索承受的荷载极其复杂,周围环境变化剧烈,因此不可避免会遭受损伤或性能退化,属于易损结构[1]。为了保证桥梁结构运营安全,需要及时、正确地识别索结构的损伤特性,并采取有效的措施保证结构安全可靠[2]。而这些损伤特征信息往往淹没在各种环境因素的影响中,其中以温度变化影响较为突出[3]。为此研究索结构在温度变化时的振动特性就变得非常重要。
无论是理论研究[4-10]还是工程实践[11-12],研究人员非常关注温度效应和损伤效应对频率、振型和张拉力等振动特征的影响。一方面,研究人员建立了考虑温度效应影响下拉索静、动力学分析模型;另一方面,基于拉索损伤程度、位置和范围三个参数,建立了拉索损伤状态下分析模型。然而悬索作为一类同时包含二次和三次非线性项的柔性结构,在荷载激励下会产生丰富的非线性动力学现象。实验结果表明[13]:温度变化对悬索非线性振动中的分叉现象有显著影响。因此基于考虑温度效应影响下的非线性动力学模型,深入研究温度变化对悬索非线性振动特性影响,既可以丰富拉索非线性动力学理论研究,还可以为结构损伤识别提供参考和依据。
本文以悬索为例,基于增量热场理论,建立考虑温度变化影响的动力学模型,推导非线性运动微分方程。采用多尺度法,求解其非线性主共振响应的高阶近似解及幅频响应方程。通过算例研究温度变化对不同垂跨比悬索的非线性主共振响应影响。
1 数学模型
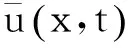

图1 悬索构形及特性
1.1 运动微分方程
基于悬索静平衡和热应力平衡状态时的平衡方程,受外激励作用下悬索的运动方程可以表示为:

(1)

(2)
其中:cu和cv分别表示悬索在u和v方向阻尼系数。
根据链式法则,结合热应力状态时的平衡方程,可得[5]:

(3)
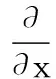
(4)
式中:Ξ和Ξd分别表示在热应力平衡状态下的静拉力及在运动状态下增大的动拉力沿悬索弦向分量,其表达式分别为:
和
由于温度变化会影响悬索垂度和张拉力,因此引入了两个无量纲参数κ2和χ2。基于拟静态假设,悬索面内振动的运动方程为:

(5)
式中:Ω为外激励的频率。
为研究简便,引入以下无量纲参数:
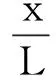

(6)
将式(6)代入式(5)中,略去表达式的上标星号,则相应的无量纲运动方程为:

(7)
式中:y(x)=4fx(1-x)和f=b/L。
1.2 Galerkin离散
假设悬索是由正对称和反对称模态组成的多自由度系统,利用Galerkin法对式(7)进行无穷维离散,面内运动的位移函数表示为:
φ(x)
(8)
式中:N为模态离散的数目;qn(t)是广义坐标函数;φ(x)为n阶模态函数。
将式(8)代入式(7)中,可得:

(9)



由此可见温度变化并没有改变悬索运动微分方程的形式,而是通过引入的两个无量纲参数(χ2和κ2)来体现温度变化的影响。
2 主共振响应分析
对于有阻尼系统,多尺度法处理起来更加方便,而且由于低阶的多尺度近似解有可能产生定性的误差,因此本文采用高阶的多尺度法求解悬索非线性主共振响应的近似解[14]。
此时外激励频率表示为:
Ωn=ωn+ε2σn1+ε4σn2
(10)
式中:ωn为线性分析得到的模态频率;ε为无量纲小参数;σn1和σn2为前两阶调谐参数。
利用多尺度法可得系统的幅频响应方程:
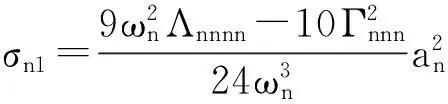
(11)

(12)
而总的调谐参数参数表示为:
σn=σn1+σn2
(13)
因此系统的稳态响应解为:

(14)
3 算例分析
假设悬索弹性模量和阻尼系数均与温度变化无关,其各项物理参数为:L=200 m、A=7.069×10-2m2、E=200 GPa、ρ=7 800 kg/m3、α=1.2×10-5℃以及g=9.81 m/s2。无量纲化后的激励幅值以及阻尼系数分别为0.003和0.002 5。
图2描绘了在整体均匀温度变化影响下,悬索前四阶模态频率(前两阶正/反对称模态)与Irvine参数λ2的关系曲线。由图可知,前四阶模态频率受温度变化的影响明显,尤其是第一阶正对称模态频率[15]。反对称模态频率虽与温度变化呈现反比例关系,但是其模态振型不受温度变化的影响。一阶正/反对称模态频率之间存在交点,在交点附近容易发生模态间的内共振以及能量传递现象。然而在温度变化的影响下,交点的位置发生了漂移,表明悬索内共振响应受温度变化影响明显。
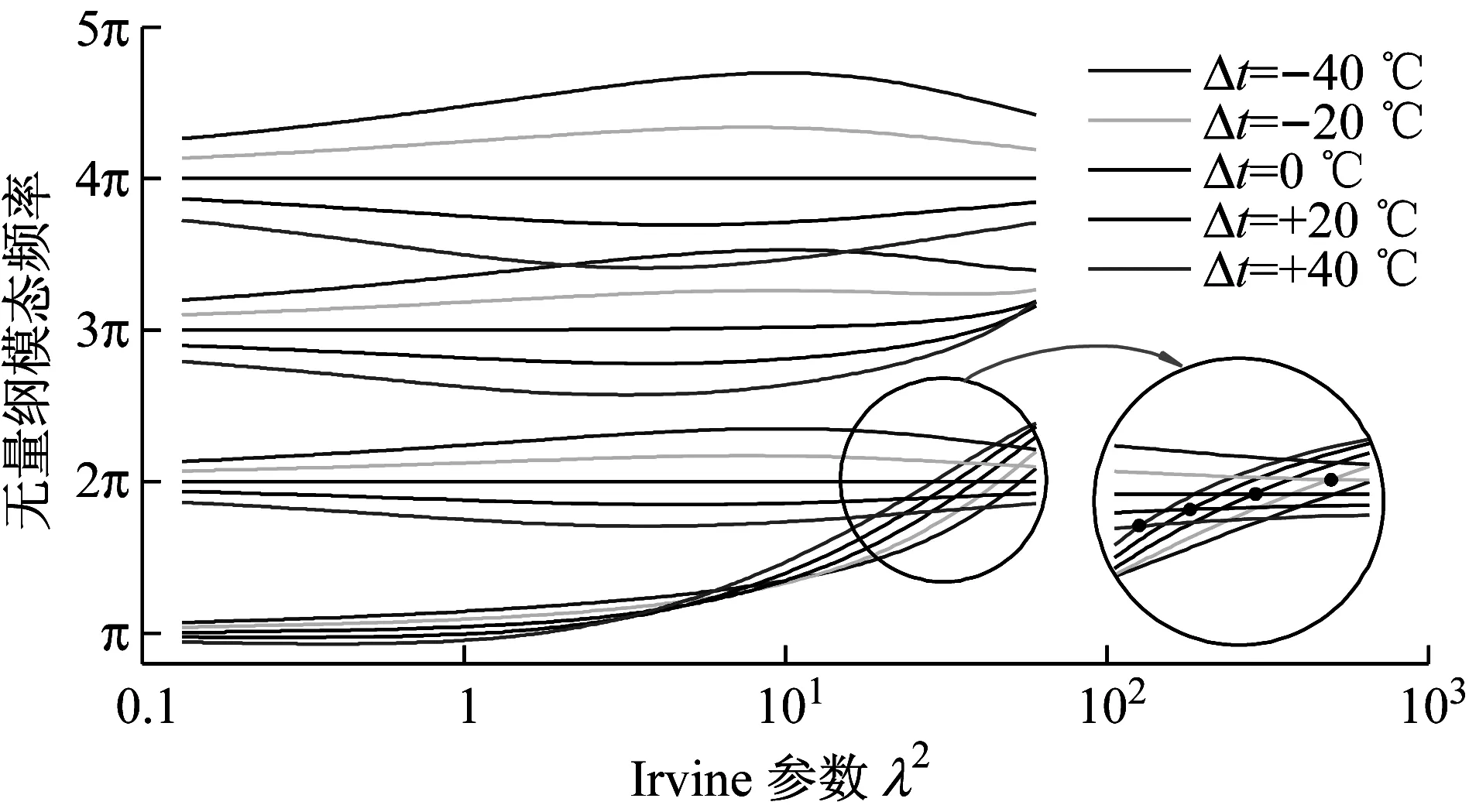
图2 温度变化对Irvine参数与无量纲模态频率关系曲线影响
Fig.2 Temperature effects on relationship curves between Irvine parameter and non-dimensional mode frequencies
图3描绘了温度变化对四种垂跨比悬索主共振幅频响应曲线的影响。温度变化和线性频率之间的正、反比例关系与初始张拉力密切相关[6]。而悬索平方和立方非线性项系数的大小则和温度变化呈现出明显的正比例关系,即温度上升,非线性项系数增大,反之则减小。
对于图3(a),此时悬索垂跨比约为0.006,对应Irvine参数约为1.45,从线性结果分析来看,温度上升,线性频率下降,温度下降,线性频率上升。此时从定性角度而言,悬索均表现出明显的“硬”弹簧特性(曲线向右偏转);从定量角度来看,温度变化对主共振响应影响比较有限。由此推断,当悬索垂跨比非常小时,温度变化对其非线性振动特性影响不明显。
图3(b)中,悬索的垂跨比为0.01,Irvine参数约为6.72。线性分析结果表明:无论温度上升还是下降,线性频率均会增大。而从非线性分析结果来看,在不考虑温度变化(Δt=0 ℃)和温度下降(Δt=-40 ℃)两种情况下,悬索的幅频响应曲线均向右偏转。而当温度上升时(Δt=+40 ℃),悬索会表现出先偏“软”再偏“硬”的振动特性,即曲线先向左然后向右偏转。这一现象的原因在于当温度上升时,悬索平方非线性项系数受温度变化影响最为明显,此时平方非线性在振动中占主导地位,从而使得曲线向左偏转。
悬索的垂跨比进一步增大(f=0.015),对应的Irvine参数也进一步增加(λ2=21.92),此时温度变化影响下的幅频响应曲线如图3(c)所示。当温度上升时,悬索线性频率也随之增大。而对于主共振响应而言,无论温度是上升还是下降,悬索均表现出先“软”后“硬”的振动特性。但是从定量角度而言,当温度上升时,升温对立方非线性项系数的影响程度明显大于降温,因此随着温度上升,曲线向右偏转程度明显加剧。
最后悬索垂跨比进一步增大至0.02,对应的Irvine参数为60.04。由图3(d)所示,温度变化明显改变了悬索主共振响应的振动特性。特别是当温度上升时,此时悬索的“软”弹簧特性几乎消失。尽管平方非线性项的系数随着温度上升而增加,但是此时立方非线性项的系数随着温度的上升增大约为3倍。因此“硬”弹簧特性占据主导地位,此时曲线迅速向右偏转。

(a)f=0.006
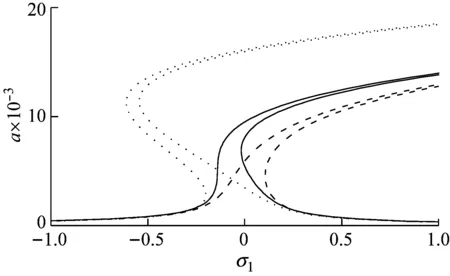
(b)f=0.01

(c)f=0.015

(d)f=0.02
图3 温度变化对悬索幅频响应曲线影响:
Fig.3 Temperature effects on frequency response curves of the suspended cable
4 结 论
平方和立方非线性项的系数与温度变化呈现出明显的正比例关系,而线性项系数与温度变化之间的比例关系则和悬索垂跨比密切相关;悬索非线性主共振响应受温度变化影响较为明显,与其垂跨比密切相关,但当垂跨比很小(初始张拉力很大),温度变化对悬索振动特性影响明显减弱;悬索主共振响应特性在温度变化影响下,有可能发生定性和定量地改变,取决于线性项、平方和立方非线性项受温度变化的影响程度;相同程度的升温和降温对悬索振动特性影响不对称。
[1] 李兆霞, 王滢, 吴佰建, 等. 桥梁结构劣化与损伤过程的多尺度分析方法及其应用[J]. 固体力学学报, 2010, 21(6): 731-756.
LI Zhaoxia, WANG Ying, WU Baijian, et al. Multi-scale modeling and analyses on structural deterioration and damage in long-span bridges and its application[J]. Chinese Journal of Solid Mechanics, 2010, 21(6): 731-756.
[2] 李爱群, 丁幼亮, 王浩, 等. 桥梁健康监测海量数据分析与评估—“结构健康监测”研究进展[J]. 中国科学: 科学技术, 2012, 42(8): 972-984.
LI Aiqun, DING Youliang, WANG Hao, et al. Analysis and assessment of bridge health monitoring mass data-progress in research/development of Structural Health Monitoring[J]. Sci China Tech Sci, 2012, 42(8): 972-984.
[3] 陈波, 郑瑾, 王建平. 桥梁结构温度效应研究进展[J]. 武汉理工大学学报, 2010, 32(24): 79-83.
CHEN Bo, ZHENG Jin, WANG Jianping. State-of-the-art of the temperature effects of bridges[J]. Journal of Wuhan University of Technology, 2010, 32(24): 79-83.
[4] TREYSSEDE F. Free vibrations of cables under thermal stress[J]. Journal of Sound and Vibration, 2009, 327(1): 1-8.
[5] LEPIDI M, GATTULLI V. Static and dynamic response of elastic suspended cables with thermal effects[J]. International Journal of Solids and Structures, 2012, 49(9): 1103-1116.
[6] 赵珧冰, 孙测世, 彭剑, 等. 温度变化对拉索频率与索力的影响[J]. 应用力学学报, 2013, 30(6): 904-908.
ZHAO Yaobing, SUN Ceshi, PENG Jian, et al. The effects of temperature changes on the frequencies and tension forces of cable[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 904-908.
[7] 汪峰, 陈福青, 文晓旭, 等. 考虑温度影响的斜拉索参数振动模型及响应分析[J] 重庆交通大学学报(自然科学版), 2016, 35(2): 1-5.
WANG Feng, CHEN Fuqing, WEN Xiaoxu, et al. Analysis of cable parametric vibration model and response with consideration of temperature effect[J]. Jounral of Chongqing Jiaotong University (Natural Science), 2016, 35(2): 1-5.
[8] LEPIDI M, GATTULLI V, VESTRONI F. Static and dynamic response of elastic suspended cables with damage[J]. International Journal of Solids and Structures, 2007, 44: 8194-8212.
[9] 王立彬, 王达, 吴勇. 损伤拉索的等效弹性模量及其参数分析[J]. 计算力学学报, 2015, 32(3): 339-345.
WANG Libin, WANG Da, WU Yong. The equivalent elastic modulus of damaged cables and parameter analysis[J]. Chinese Journal of Computational Mechanics, 2015, 32(3): 339-345.
[10] ZHU J, YE G R, XIANG Y Q, et al. Dynamic behavior of cable-stayed beam with localized damage[J]. Journal of Vibration and Control, 2011, 17(7): 1080-1089.
[11] 樊可清, 倪一清, 高赞明. 大跨度桥梁模态频率识别中的温度影响研究[J]. 中国公路学报, 2006, 19(2): 67-73.
FAN Keqing, NI Yiqing, GAO Zanming. Research on temperature Influences in long-span bridge[J]. China Journal of Highway and Transport, 2006, 19(2): 67-73.
[12] 李顺龙, 李惠, 欧进萍, 等. 考虑温度和风速影响下的桥梁结构模态参数分析[J]. 土木工程学报, 2009, 42(4): 100-106.
LI Shunlong, LI Hui, OU Jinping, et al. Identification of modal parameters of bridges considering temperature and wind effects[J]. China Civil Engineering Journal, 2009, 42(4): 100-106.
[13] REGA G, ALAGGIO R. Experimental unfolding of the nonlinear dynamics of a cable-mass suspended system around a divergence-hopf bifurcation[J]. Journal of Sound and Vibration, 2009, 322(3): 581-611.
[14] ZHAO Y B, SUN C S, WANG Z Q, et al. Analytical solutions for resonant response of suspended cables subjected to external excitation[J]. Nonlinear Dynamics, 2014, 78: 1017-1032.
[15] 赵珧冰, 孙测世, 彭剑, 等. 不同初拉力拉索对温度变化的敏感性分析[J]. 中南大学学报(自然科学版), 2014, 45(5): 1680-1685.
ZHAO Yaobing, SUN Ceshi, PENG Jian, et al. Sensitivity analysis of different initial tension forces of suspended cable to temperature changes[J]. Journal of Central South University(Science and Technology), 2014, 45(5): 1680-1685.
Effects of temperature changes on primary resonances of suspended cables
ZHAO Yaobing1, PENG Jian2,3
(1. College of Civil Engineering, Huaqiao University, Xiamen 361021, China;2. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;3. College of Civil Engineering, Hunan University, Changsha 410082, China)
Based on the incremental thermal field theory, the nonlinear vibration equations of a suspended cable under harmonic excitation considering uniform temperature variation were derived. Galerkin method was used to discretize the nonlinear vibration equations and the discretized equations were analyzed linearly. The higher order approximate solution and the amplitude-frequency response equation were obtained with the multi-scale method. The effects of temperature changes on the first 4 orders modal frequencies and amplitude-frequency response curves of the suspended cable with different Irvine parameters were studied with numerical examples. The results showed that modal shapes, modal frequencies and primary resonance responses of the suspended cable are obviously affected by temperature changes, and they are closely related to Irvine parameters of the suspended cable; the suspended cable’s nonlinear vibration characteristics may be changed quantitatively and qualitatively by temperature effects, they are dependent on the effects of temperature changes on coefficients of the linear term, the square one and the cubic one; the effects of temperature increase and its decrease at the same level on the vibration characteristics of the suspended cable are not symmetric.
suspended cable; temperature variations; multi-scale method; primary resonance
国家自然科学基金(11602089; 11402085); 福建省自然科学基金青年创新(2016J05011); 福建省中青年教师教育科研项目(JAT160025);华侨大学高层次人才科研启动费(15BS409)
2015-12-30 修改稿收到日期:2016-06-16
赵珧冰 男,博士,讲师,1988年9月生
TH1
A
10.13465/j.cnki.jvs.2017.15.036

