轮辐板式局域共振声子晶体隔振器的振动特性研究

赵浩江， 宋 扬， 刘荣强

(1.中国科学院 长春光学精密机械与物理研究所，长春 130033；2.东北林业大学 机电工程学院，哈尔滨 150040；3.哈尔滨工业大学 机电工程学院，哈尔滨 150001)

轮辐板式局域共振声子晶体隔振器的振动特性研究

赵浩江1， 宋 扬2， 刘荣强3

(1.中国科学院 长春光学精密机械与物理研究所，长春 130033；2.东北林业大学 机电工程学院，哈尔滨 150040；3.哈尔滨工业大学 机电工程学院，哈尔滨 150001)

基于局域共振带隙机理，设计一种新型的轮辐式三组元凸起声子晶体板隔振器，并结合理论带隙计算、有限元仿真和试验测试对隔振器的低频隔振特性进行分析和验证。研究发现，以轮辐形板为三组元凸起声子晶体板的基板比圆形板容易获得更大的带隙频率范围内衰减幅度。基板上开孔可以提高带隙的终止频率，从而增大带隙宽度。选用三种双侧凸起的原胞为轮辐板的基本单元，设计了三种单轮辐板隔振器，以及不同轮辐板排列组合的六种双轮辐板和六种三轮辐板隔振器。实测数据表明，单轮辐板、双轮辐板以及三轮辐板隔振器在其带隙频率范围内平均衰减幅度分别可以达到24 dB、34 dB以及38 dB。这种结构设计及研究结果在低频减振领域有潜在的应用前景。

声子晶体;局域共振;隔振器;低频带隙

结构振动广泛存在于各个工程领域中，抑制有害的结构振动一直是工程技术中迫切需要解决的问题之一。声子晶体概念的提出[1-2]为结构振动抑制提供了一种新思路。声子晶体是一种具有弹性波带隙特性的人工周期材料，在带隙频率范围内的振动形式不能通过声子晶体，因此可应用于减振隔振领域。与传统的主动、被动隔振相比，声子晶体结构可实现结构与隔振系统的一体化设计，并且具有质量轻、隔振频率宽、可靠性高等优点，在工程隔振领域具有广泛的应用前景。

声子晶体按照其带隙形成机理可分为Bragg散射型和局域共振型。其中局域共振型声子晶体通过振子在特定频率范围内产生局域共振，将振动能量局域在振子内，减少振动能量在结构中的传播，可以实现对应波长远大于其晶格常数的低频带隙，即用较小的结构尺寸获取低频带隙。自刘正猷等[3]提出局域共振声子晶体的概念以来，国内外学者对这类声子晶体的带隙形成机理开展了大量的研究[4-8]。凸起型声子晶体板[9-12]是可实际应用的局域共振声子晶体结构中最重要的类型之一，它将声子晶体的振动带隙特性和板结合，通过合理设计可以达到良好的隔振效果。按组元数不同，凸起型声子晶体板可以分为单组元、双组元和三组元凸起型声子晶体板。Bilal等[13]研究了一种基板上孔和凸起周期分布的局域共振弹性超材料，发现这种结构能够产生弹簧垫效应，对凸起的局域共振特性起到放大作用，从而增宽了局域共振带隙。Hsu[14]提出了一种带“颈部”的凸起型声子晶体板，分析表明这种钢单组元结构同时具有局域共振带隙和Bragg散射带隙，并且“颈部”的结构参数对带隙具有重要影响。Wang等[15-16]研究了双侧周期凸起均质铝板的能带结构特征，发现双侧凸起对称布置时凸起的局域共振与板的Lamb模式的耦合更强，容易获得更宽的带隙。Oudich等[17]对影响二组元和三组元凸起型声子晶体板带隙的结构参数进行了分析，指出低频带隙是凸起的局域共振与平板Lamb波模态耦合的结果。Assouar等[18-19]提出二组元及三组元的双侧凸起板，研究结果表明，双侧凸起对称布置时可以增强凸起的局域共振与板Lamb模式的耦合作用，从而增大带隙宽度。Yu等[20]研究表明，以橡胶为均质板，均布钢凸起的声子晶体具有超低频局域共振带隙。但可以想象，这种结构是很难实际应用的，因为橡胶均质板很难提供结构需要的支撑强度。以上研究皆停留在“材料”层面，没有考虑机械接口、安装方式、空间尺寸等因素，不能直接用于结构隔振，因此应该设计基于凸起型声子晶体板的隔振器结构。

本文提出了一类以双侧对称凸起的三组元声子晶体轮辐板为关键元件的单向隔振器结构，并分别从结构设计、有限元仿真和实验三个方面对隔振器的振动带隙进行分析和研究。首先通过对比带隙内隔振效果，确定声子晶体板为轮辐形，并选取合适孔径的基板孔来增大带隙宽度。其次，用有限元法计算了3种不同声子晶体板原胞的理论带隙。最后，通过有限元仿真和试验测试，验证了单轮辐板、双轮辐板以及三轮辐板隔振器的低频隔振特性。实测结果证明这类轮辐式隔振器在其理论带隙频率范围内具有良好的隔振效果。

1 隔振器结构设计

1.1 振动传递路径选择

轮辐式隔振器的设计目的是隔离振源传递给有效载荷的垂直振动，因此需要考虑隔振器与振源和有效载荷的连接方式。考虑到隔振器结构的紧凑性和对称性，本文选用外包络圆直径为500 mm的凸起型声子晶体板为隔振器的核心部件。根据圆板直径选择铝合金基板厚为5 mm，凸起层为橡胶和钢，晶格常数为50 mm，基板上下两侧圆柱凸起层直径为30 mm，各凸起层厚度为5 mm。文中所用材料参数如表1所示。

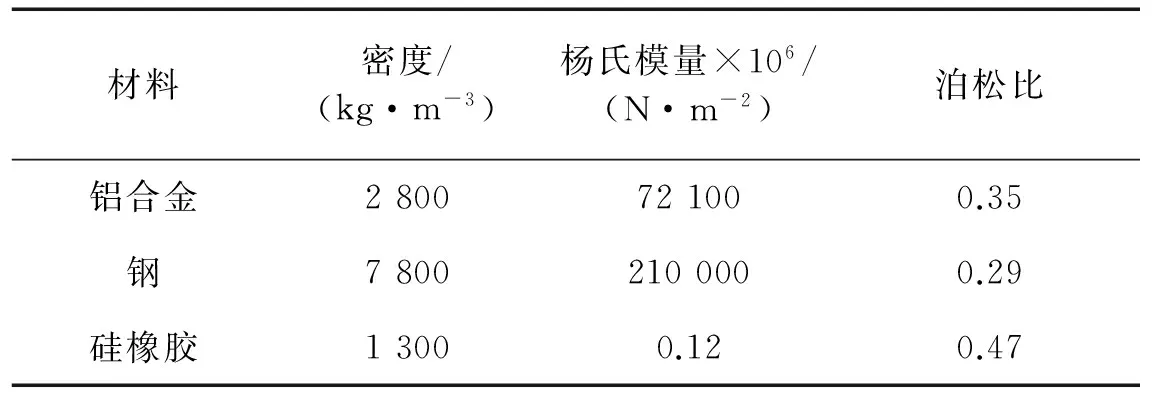
表1 计算用到的材料参数

仿真分析结果表明，振动能量在隔振器内的传递路径对隔振效果有重要影响。隔振效果与凸起的周期数目有关，周期数越多，隔振效果越好，但是当周期数达到一定数值后，继续增加周期对隔振效果的改善作用不大。若圆形基板上全部布置“橡胶层-钢层”的复合型凸起，得到的隔振器质量会很重。为了减轻重量，只在圆板上的部分位置布置凸起结构。对比下图1所示声子晶体板上振动输入输出的传递路径。图1(a)和图1(b)分别采用圆形声子晶体板和轮辐形(外包络形状为圆形)声子晶体板。考虑到结构的对称性和稳定性，分别通过基板一侧的3个连接块输入加速度激励，通过基板另一侧的3个连接块采集振动加速度响应信号。根据振动输入和输出的方式，在基板的两侧按6条轮辐状布置凸起，且每条轮辐由两排凸起构成，相邻轮辐条之间成60°间隔。其中3条轮辐对应振动输入端，另外3条对应振动输出端。

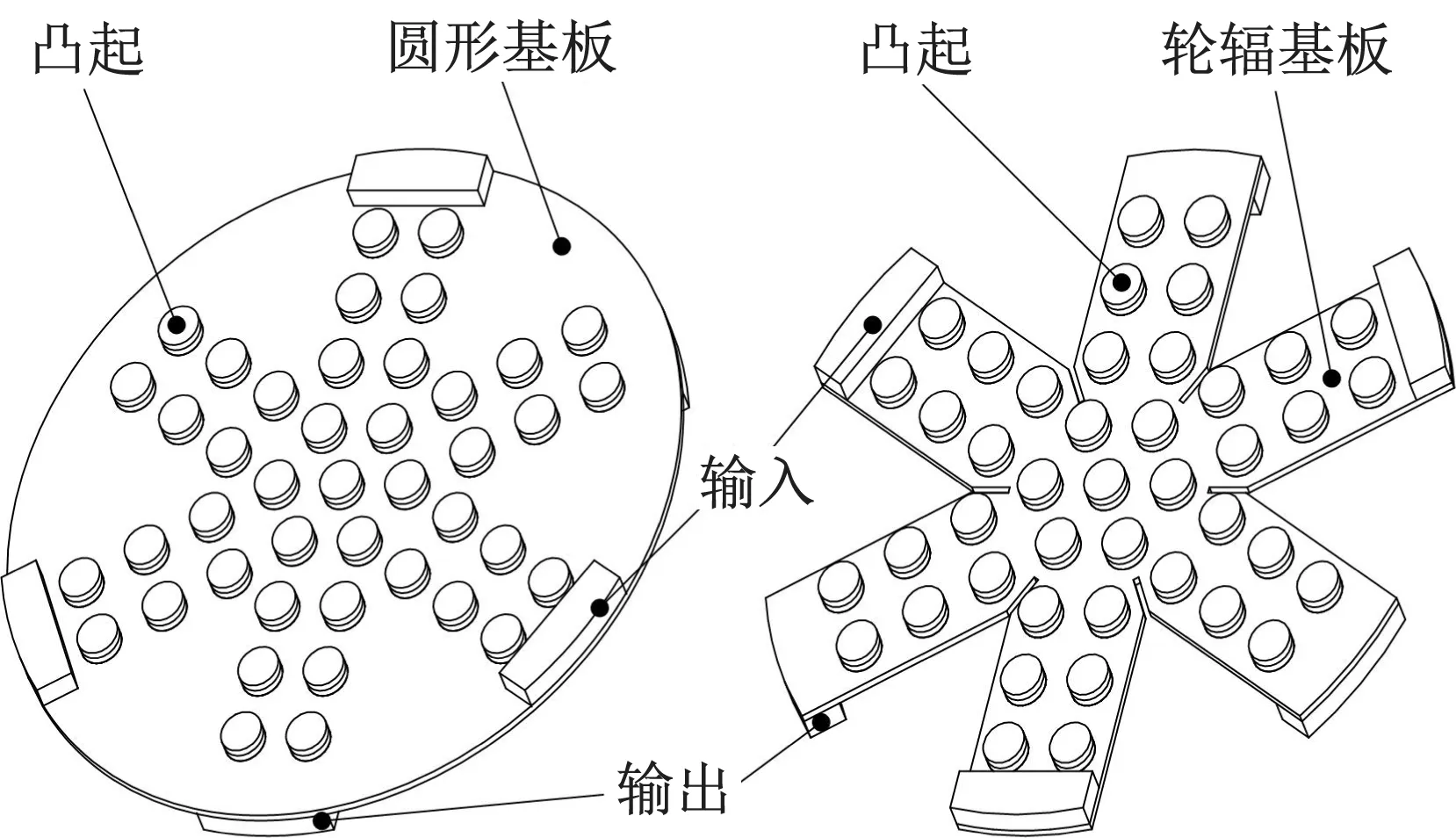
(a) 圆板输入输出 (b) 轮辐板输入输出

图1 两种不同振动传递路径

Fig.1 Two different vibration transfer paths

图2所示为以上两种布置形式的声子晶体板的振动传递特性的仿真结果(各凸起材料层厚度5 mm)，其中灰色阴影区域为有限元法计算的理论带隙频率范围。

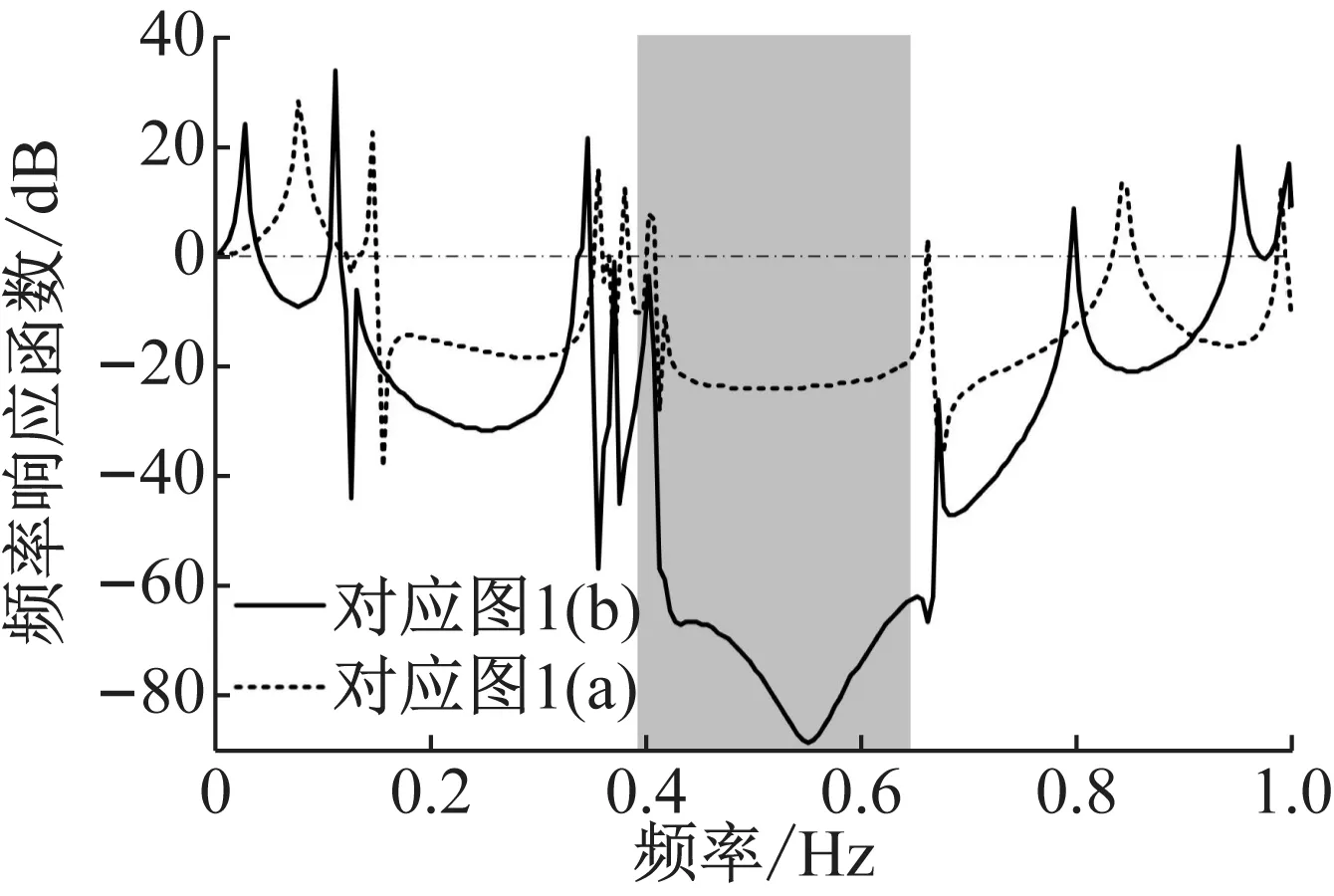
图2 两种传递路径的振动传递特性有限元仿真

可见，图1(b)所示轮辐形凸起板的振动衰减幅度要明显大于图1(a)所示的圆形凸起板。虽然圆形声子晶体板和轮辐形声子晶体板上凸起数量相同，但两者的振动传递路径不同。对于圆形声子晶体板，部分振动能量可不经过与输入和输出端对应的凸起轮辐条，而直接通过相邻的输入、输出端之间的基板部分进行传递，可能导致靠近圆板中心的凸起周期没有充分地发挥其隔振效果。但轮辐形声子晶体板的情况不同，由输入端连接块传入声子晶体板的振动能量，必须经过轮辐条上的全部凸起周期后才能通过相邻的输出端转接板传出。因此，轮辐板上全部的凸起周期能充分起到减隔振作用。

1.2 原胞结构优化

根据周期结构的Bloch定理，声子晶体的色散关系(即能带结构)可以通过计算单个原胞获得。本文采用有限元商业软件COMSOL Mutiphysics中的固体力学模块中的特征频率部分求解双侧凸起三组元声子晶体板的能带结构。在原胞的上下表面施加自由应力边界条件，并在相邻原胞分界面上施加周期边界条件：

u(x+a1,y)=u(x,y)eik1·a1

(1)

u(x,y+a2)=u(x,y)eik2·a2

(2)

式中:k=(k1,k2)是被限制在第一不可约布里渊区的波矢;a1、a2表示原胞的基矢。沿着第一不可约布里渊区的高对称边界求解特征值方程，即可得到双侧凸起声子晶体板的能带结构。

为增宽隔振带隙，在以上轮辐式板的基础上进一步优化。Bilal和Assouar的研究表明，在凸起型声子晶体板基板的无凸起部分开孔可以产生弹簧垫效应，对凸起的局域共振特性起到放大作用，达到增宽带隙的效果。受此启发，本文分析了凸起和带孔基板组合成的三组元声子晶体板上孔径对弯曲振动带隙起始位置的影响。如图3(a)所示为基板上有孔的双侧单振子凸起板原胞，以原胞基板正方形的四个角为圆心开孔。图3(b)是弯曲振动带隙起始位置随孔径dh变化的情况。

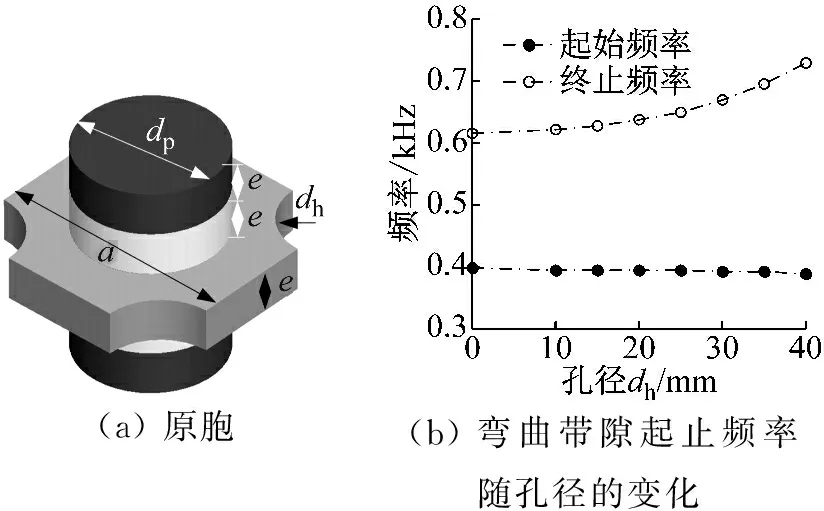
(a)原胞(b)弯曲带隙起止频率随孔径的变化

图3 基板上带孔的双侧对称凸起板

Fig.3 Symmetric DSPPCP with holes on its base plate

可见，随着孔径dh的增大，带隙起始频率基本不变，而终止频率向高频移动，导致带隙宽度增大。但孔径也不易过大，否则会使轮辐板没有足够的刚度支撑有效载荷而发生严重变形。根据以上分析，最终确定隔振器中的轮辐形双侧凸起板采用如图4所示的形式。其中凸起直径dp和孔径dh都为30 mm。

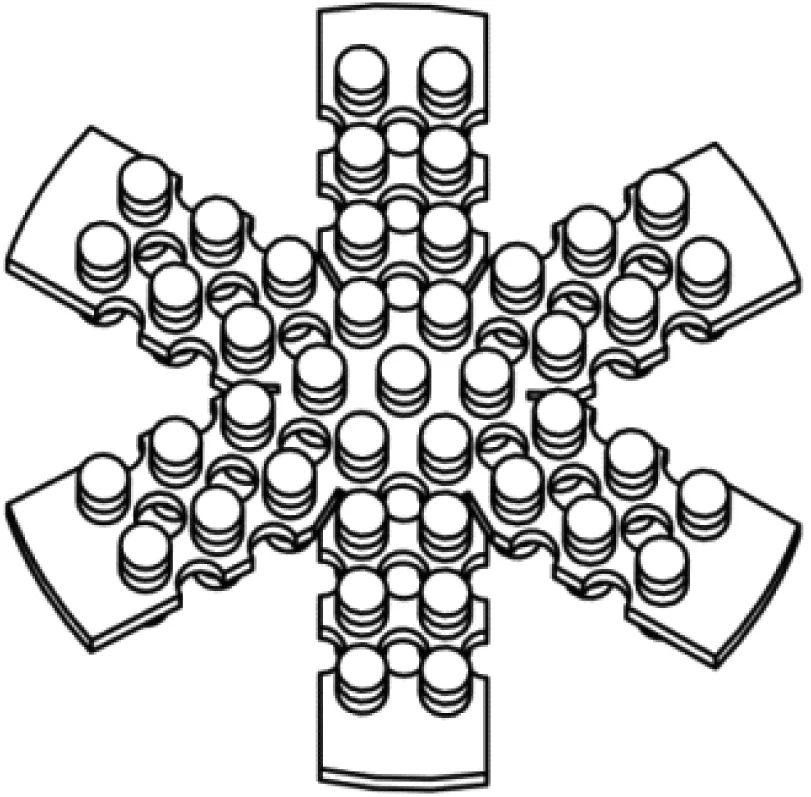
(a)轮辐板最终结构示意图 (b) 多轮辐板组合照片

图4 带孔的轮辐形双侧单振子凸起型声子晶体板

Fig.4 Spoke-like DSPPCP with holes

1.3 轮辐式隔振器的可拓展性及工作原理

以图4所示轮辐形双侧单振子凸起型声子晶体板为核心部件的轮辐板隔振器具有很好的可拓展性。根据其振动输入、输出位置的对称性特点，理论上可用连接块将无限多片轮辐板进行组合，形成含多片轮辐声子晶体板的多级单向隔振器。但在实际设计中，轮辐板的数量不宜过多，否则会降低隔振器的稳定性和可靠性。容易想到，通过结构参数和材料参数设计，使各轮辐板具有不同的带隙位置和宽度，则多片轮辐板组合可以实现不同位置和宽度的带隙的组合，使隔振器在更宽的频率范围内获得隔振效果。以三轮辐板隔振器为例说明多轮辐板隔振器的工作原理，如图5所示为三轮辐板隔振器结构爆炸图。轮辐板隔振器主要由三部分组成：与振源连接的输入端转接板、轮辐形双侧凸起声子晶体板组及与有效载荷连接的输出端转接板。板与板之间通过连接块衔接，利用连接块的厚度为声子晶体板和两转接板提供足够的间隙。相邻两板之间有3个连接块，振动能量通过连接块传入下一层轮辐板(或输出端转接板)，带隙频率内的振动能量经过轮辐板后被衰减。

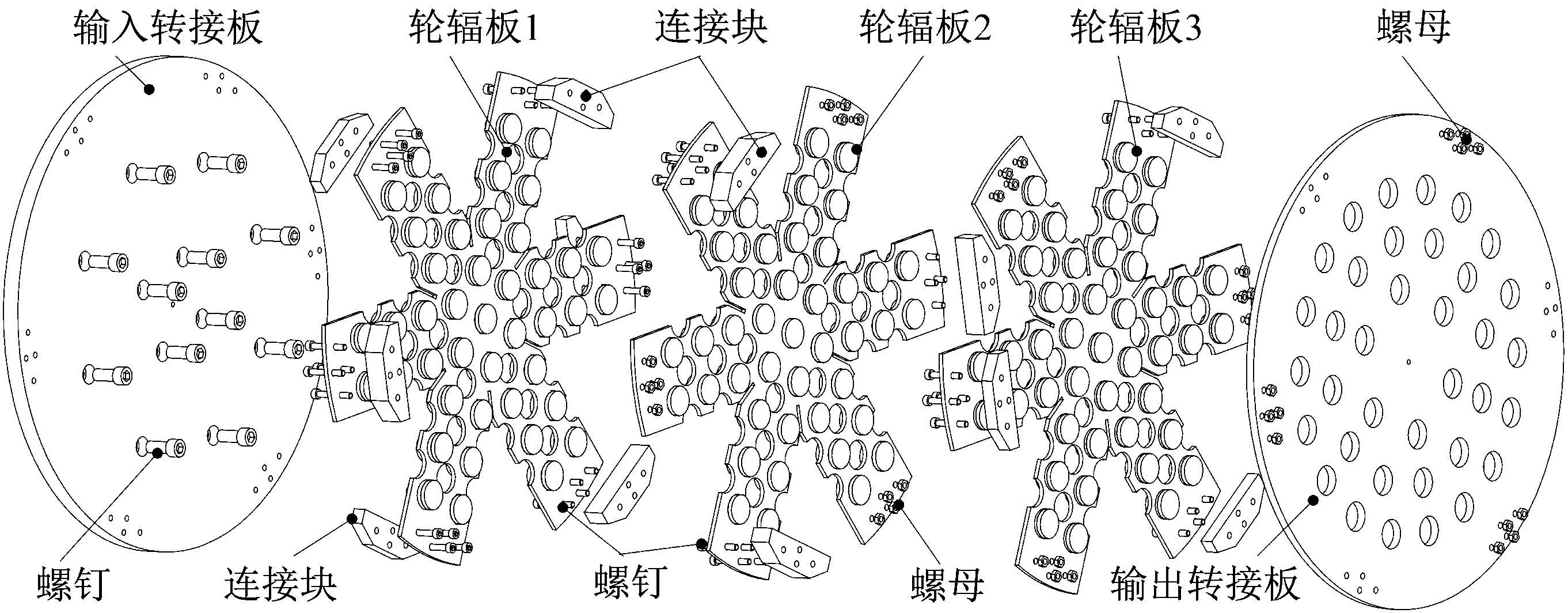
图5 三轮辐板隔振器结构

选用编号为A、B、C的3种基板上带孔的双侧对称凸起原胞，它们的外侧凸起层材料、橡胶层厚度及其弯曲振动带隙频率范围如表2所示。表中各原胞的ΓX方向能带结构如图6所示，其中黑色区域为带隙频率范围。

表2 隔振器轮辐板采用的原胞

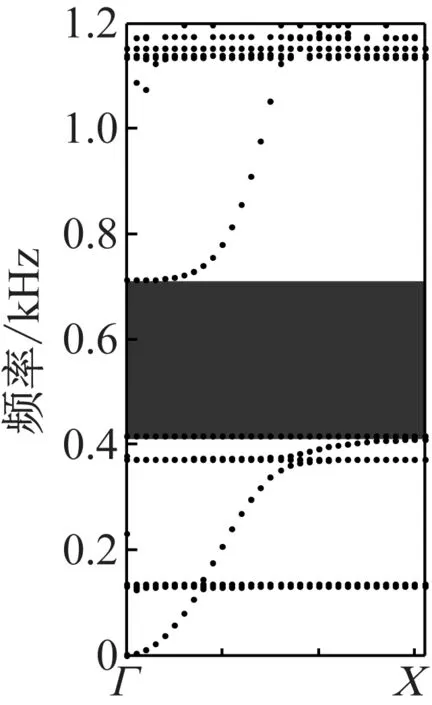
(a) A原胞

(b) B原胞

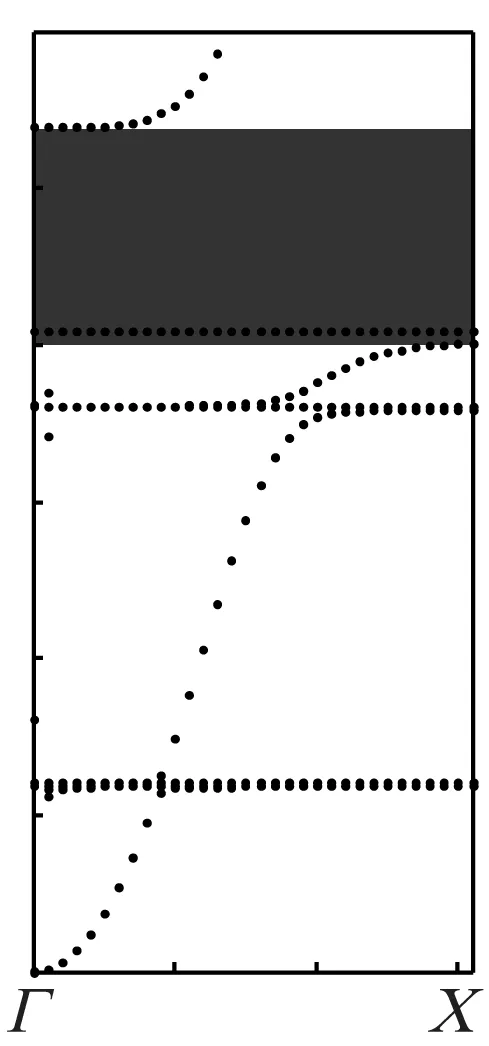
(c) C原胞

分别将含A原胞、B原胞及C原胞的轮辐板称为A板、B板和C板，含A板、B板、C板的单轮辐板隔振器命名为隔振器11、隔振器12及隔振器13。含不同原胞轮辐板(不同排列顺序)的双轮辐板隔振器及三轮辐板隔振器的编号,如表3所示。

2 隔振特性的仿真与实验

2.1 单轮辐板隔振器隔振特性

在振动台上对以上3种单轮辐板、6种双轮辐板和6种三轮辐板隔振器进行正弦扫频振动实验。如图7所示，通过控制器控制振动台输出垂直于隔振器板面的5 Hz到1 200 Hz的正弦扫频激励，激励加速度为1 g。采集上端盖的加速度信号，并与振动台输入加速度信号进行对比，经过数据处理后获得单轮辐板隔振器的振动传递特性曲线。

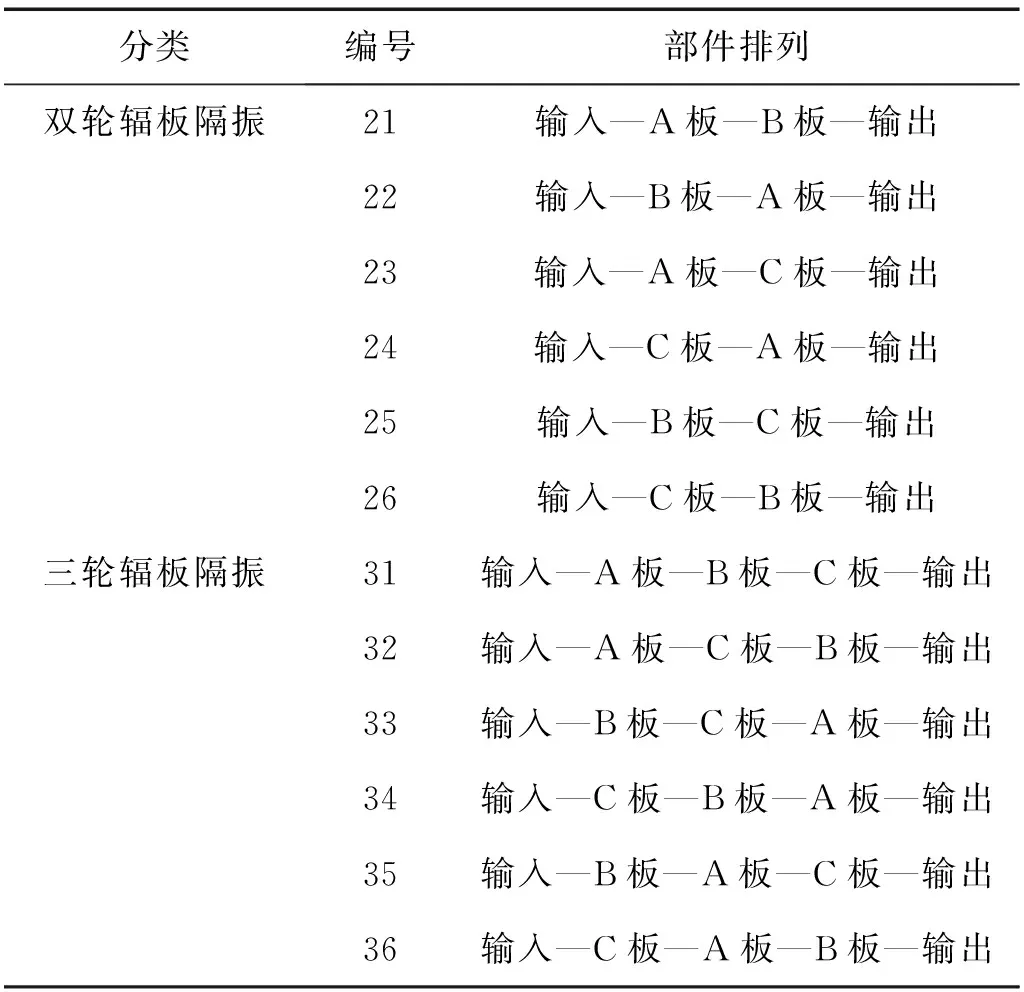
表3 多轮辐板隔振器编号

图8为实验测试和有限元仿真获得的3种单轮辐板隔振器的振动传递特性曲线。图中阴影部分对应图6中的各原胞带隙的频率范围，实线为实验测得频响曲线，虚线为有限元仿真频响曲线。隔振器11、12、13的带隙频率范围内的实测最大衰减幅度分别为31.0 dB、37.1 dB和32.0 dB，带隙内平均实测衰减幅度(带隙内各采样点衰减幅度之和除以采样点数)分别为24.2 dB、29.5 dB和25.6 dB。由图8知，3种单轮辐板隔振器的振动传递特性的有限元仿真结果和实验测试结果，除前两阶固有频率的位置较为一致，其它高阶共振频率的位置都有较大差异，但是仿真和实验曲线在理论带隙频率范围内都有明显衰减。

图9所示为隔振器11的前两阶固有频率对应振型及带隙内频率对应振型。可以看出，单轮辐板隔振器的一阶振型是以输出转接板为刚体质点、以轮辐板为弹簧的“弹簧-质点”垂直于板方向的往复振动，因此轮辐板主要提供刚度模量，增加的凸起对轮辐板刚度的影响不大，因此对固有频率改变不明显。而二阶振型是以输入转接板和输出转接板为静止点，轮辐板受其自身质量影响做的凹凸振动，因此增加的凸起质量降低了固有频率。由带隙内振型可知，振动能量局域在与振动输入转接板连接的轮辐的前几个凸起上，凸起局域共振产生的反作用力有效地抵消了部分振动激励力，振动在带隙频率范围内的传递被有效降低，使传递到输出转接板的振动能量大幅度降低。

(a) 单轮辐板隔振器

(c) 三轮辐板隔振器

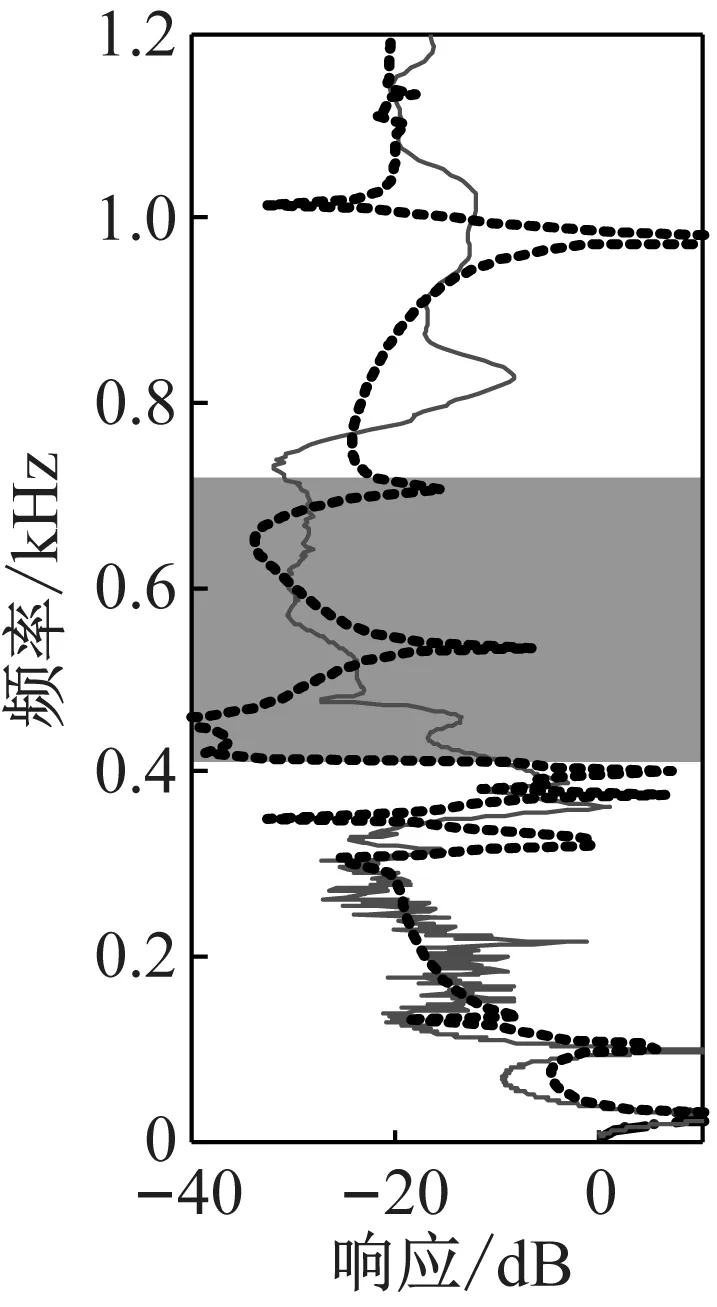
(a) 隔振器11

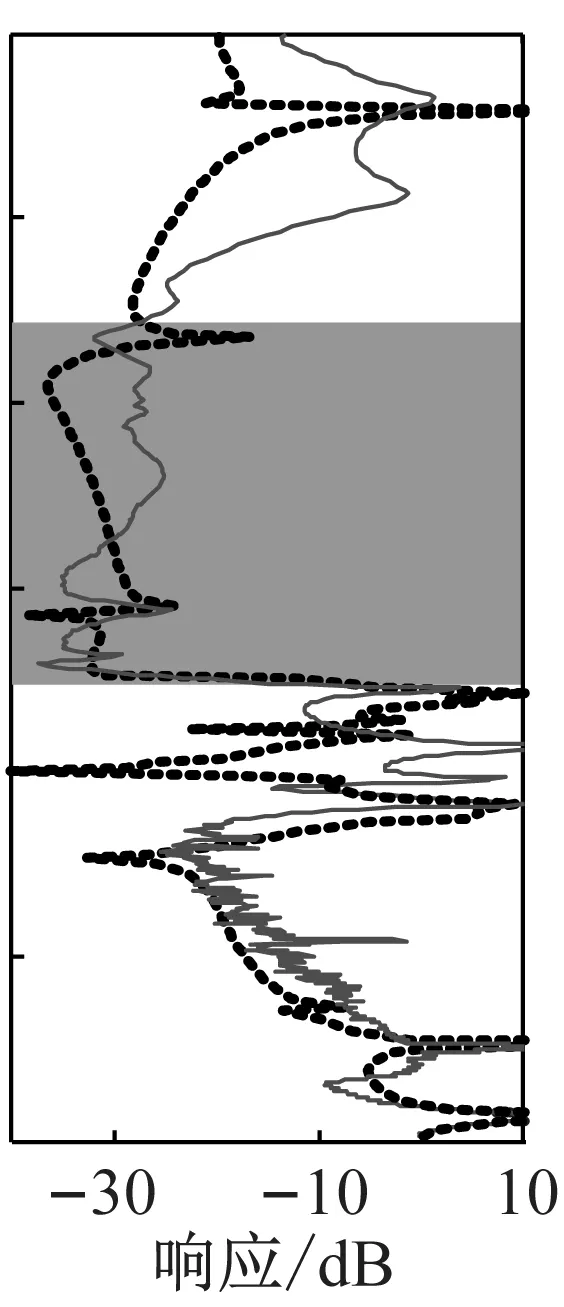
(b) 隔振器12

(c) 隔振器13

(a) 一阶振型27 Hz

(b) 二阶振型100 Hz

2.2 双轮辐板隔振器隔振特性

图10为6种双轮辐板隔振器振动传递特性的有限元仿真与实验测试结果的对比。其中浅灰色区为各轮辐板对应的理论带隙频率范围，深灰色区为带隙重叠范围。可见，隔振器21和22，以及隔振器25和26的两个理论带隙分别具有重合区域，并且在重合后连成的整个带隙范围内振动都有明显的衰减。隔振器23和24的两个理论带隙不重合，但在两个分离的带隙频率范围内振动也有明显的衰减。注意到，虽然隔振器21和22、隔振器23和24以及隔振器25和26具有相同的理论带隙范围，但由于轮辐板的排列顺序不同，带隙范围内的振动衰减幅度有显著差异。表4给出6种双轮辐板隔振器在其理论带隙频率范围内(图10中灰色区域)的实测最大衰减幅度、平均衰减幅度以及带隙重叠区内平均衰减幅度。

理论带隙频率范围内，整体上隔振器21比隔振器22的实测衰减幅度大，尤其是在理论带隙重合区，衰减幅度明显比非重合区大。隔振器21带隙内的衰减最高达到53.2 dB，带隙内总(两带隙连成的总带隙范围内)平均衰减达39.9 dB；而隔振器22最高能达到47.8 dB，带隙内总平均衰减达37.8 dB。对比隔振器23和隔振器24，可以发现隔振器24在C原胞的理论带隙内的衰减(平均32.0 dB)强于隔振器23在相同频率范围内的衰减(平均24.7 dB)。这是由于隔振器23的振动能量首先经过A原胞轮辐板，而隔振器24的振动能量首先经过C原胞轮辐板。对于隔振器23，振动能量经过A原胞轮辐板后引起A原胞轮辐板在C原胞的理论带隙频率范围内的大幅度振动，降低了后续C原胞轮辐板的隔振效果。对比隔振器25和隔振器26的隔振器效果可以看出，两隔振器在其组成轮辐板的理论带隙范围内的振动都有显著衰减。其中隔振器25的带隙内最大实测衰减幅度可以达到49.8 dB，而隔振器26的带隙内最大衰减幅度可以达到46 dB左右。隔振器26比隔振器25在带隙范围内的衰减幅度更为平稳，没有出现像隔振器25那样的多个带隙内的固有频率峰值，隔振器26带隙内总平均衰减幅度达到40 dB。

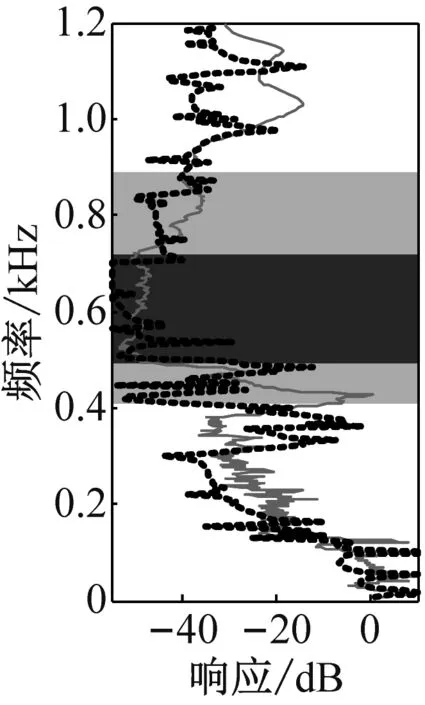
(a) 隔振器21

(b) 隔振器22

(c) 隔振器23

(d) 隔振器24

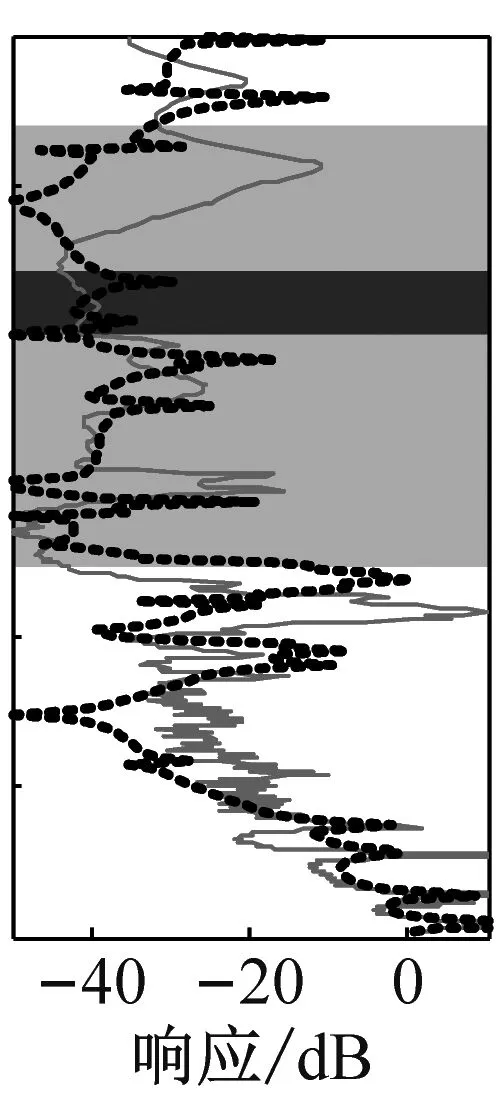
(e) 隔振器25

(f) 隔振器26

Tab.4 Attenuation amplitude in the vibration band gaps of isolators with two spoke-like plates

隔振器编号带隙内最大衰减/dB带隙内平均衰减/dB第1带隙第2带隙第1带隙第2带隙总平均重叠区2153.253.239.745.939.949.22247.847.736.741.337.841.82343.837.232.924.730.1———2442.639.735.132.034.0———2549.844.638.133.235.841.42646.045.439.940.940.041.9

以隔振器26为例，分析双轮辐板隔振器的振型特征。如图11所示的3个振型分别对应隔振器26的一阶固有频率、一阶带隙以及二阶带隙。图示振型下隔振器26的输入转接板在上、输出转接板在下。可见，双轮辐板隔振器的一阶振型以输出转接板作刚体，以两轮辐板为弹簧作垂直于板面的往复振动。而在一阶带隙(B原胞的理论带隙)内505 Hz对应的振型中，振动首先经过C原胞轮辐板引起了6个轮辐明显的弯曲变形，然后才传递到B轮辐板引起凸起的局域共振，即振动在被抑制前首先被放大了，影响了隔振器的整体隔振效果。而对于二阶带隙(C原胞的理论带隙)内805 Hz对应的振型，振动在被B轮辐板放大之前首先经过了C轮辐板上凸起局域共振的抑制，相对于C轮辐板，其后的B轮辐板几乎没有位移。

(a) 一阶固有频率15 Hz

(b) 一阶带隙内振型505 Hz

(c) 二阶带隙内振型805 Hz

2.3 三轮辐板隔振器隔振特性

由以上单轮辐板隔振器和双轮辐板隔振器的振动传递特性曲线可见，随着频率和轮辐板的增加，虽然总体上各带隙内的振动衰减趋势一致，但仿真曲线和实验曲线之间的误差越来越大，除前两阶固有频率峰值位置吻合较好之外，其它的各峰值位置都存在误差。这是由于仿真时未考虑材料阻尼、连接强度、加工误差等因素的影响。因此，隔振特性以振动实验的实测结果为准，而图12只给出以上6种三轮辐板隔振器振动传递特性的实验测试结果。

可见，隔振器的三个理论带隙分别两两重合，并且在重合后形成的整个带隙范围内振动都有明显的衰减。轮辐板排列顺序对三轮辐板隔振器的带隙内的振动衰减幅度也有明显影响，不同的排列方式分别在不同频率范围内获得最大衰减幅度。表5给出6种三轮辐板隔振器在其理论带隙频率范围内的实测最大衰减幅度、平均衰减幅度以及带隙重叠区内平均衰减幅度。其中带隙A、带隙B和带隙C分别表示A原胞、B原胞和C原胞的理论带隙。对比可知，6种三轮辐板隔振器的带隙内最大振动衰减幅度都在52 dB以上，总平均衰减幅度都在38 dB以上，三轮辐板隔振器的振型与双轮辐板相似，在此不再赘述。

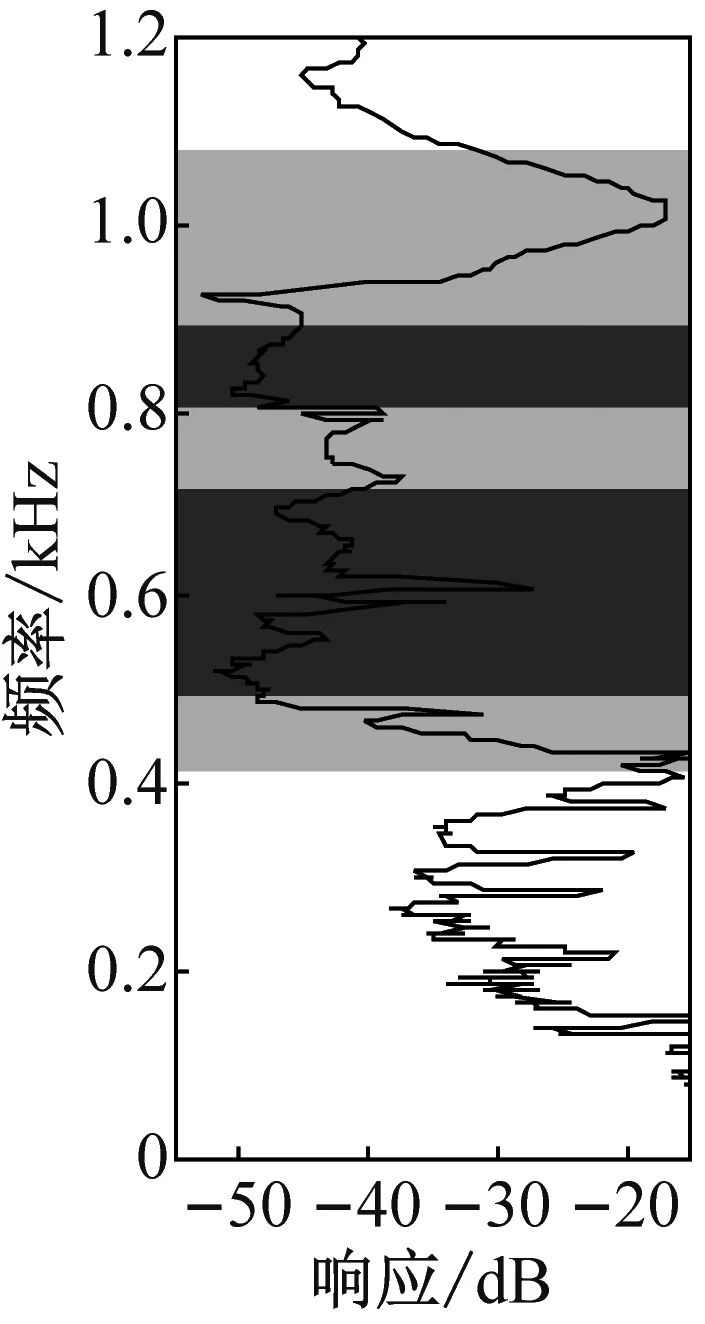
(a) 隔振器31

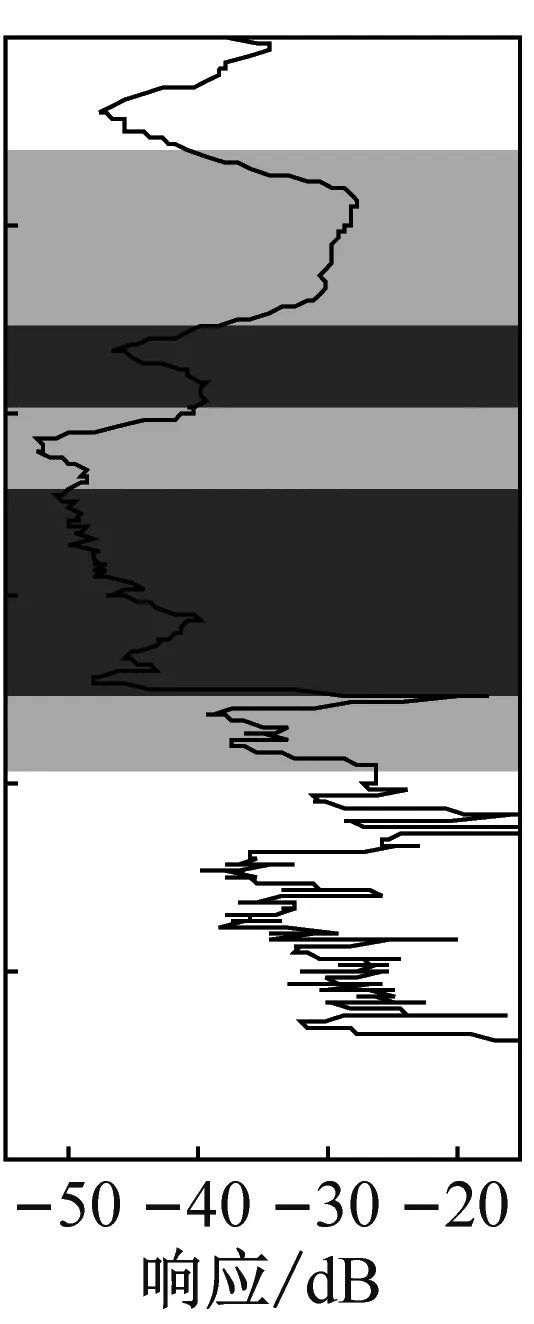
(b) 隔振器32

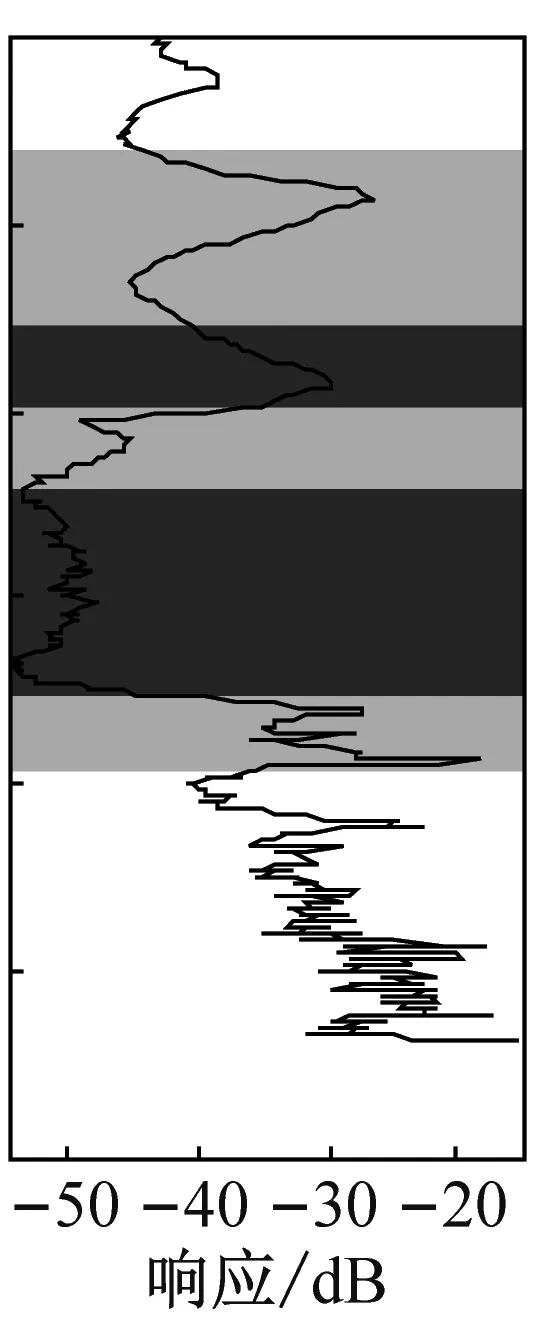
(c) 隔振器33

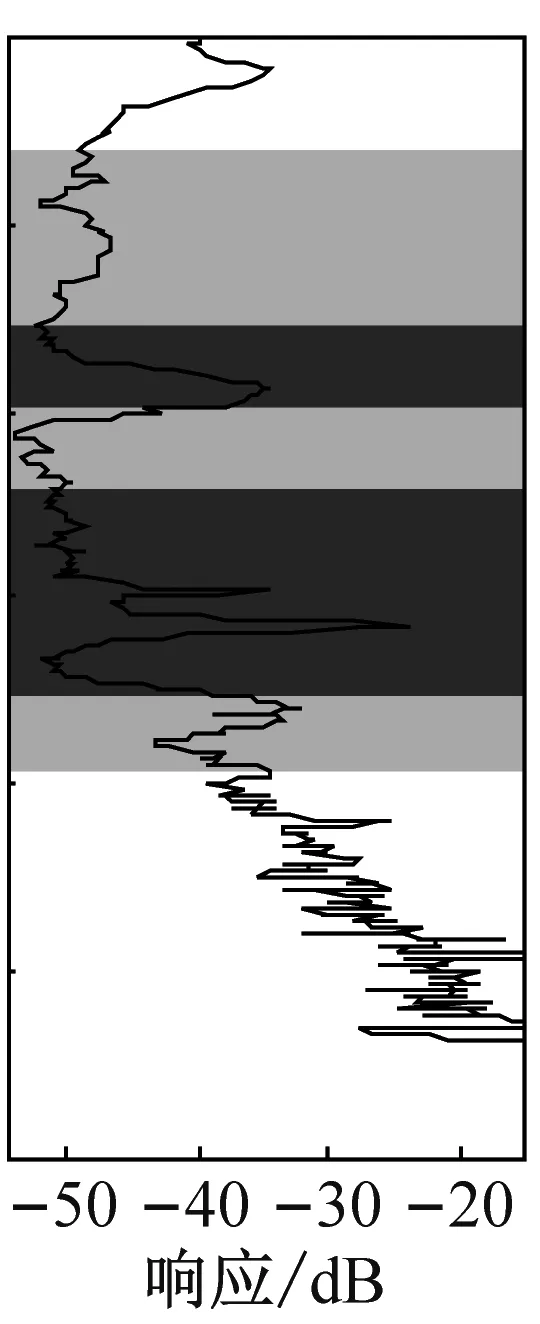
(d) 隔振器34

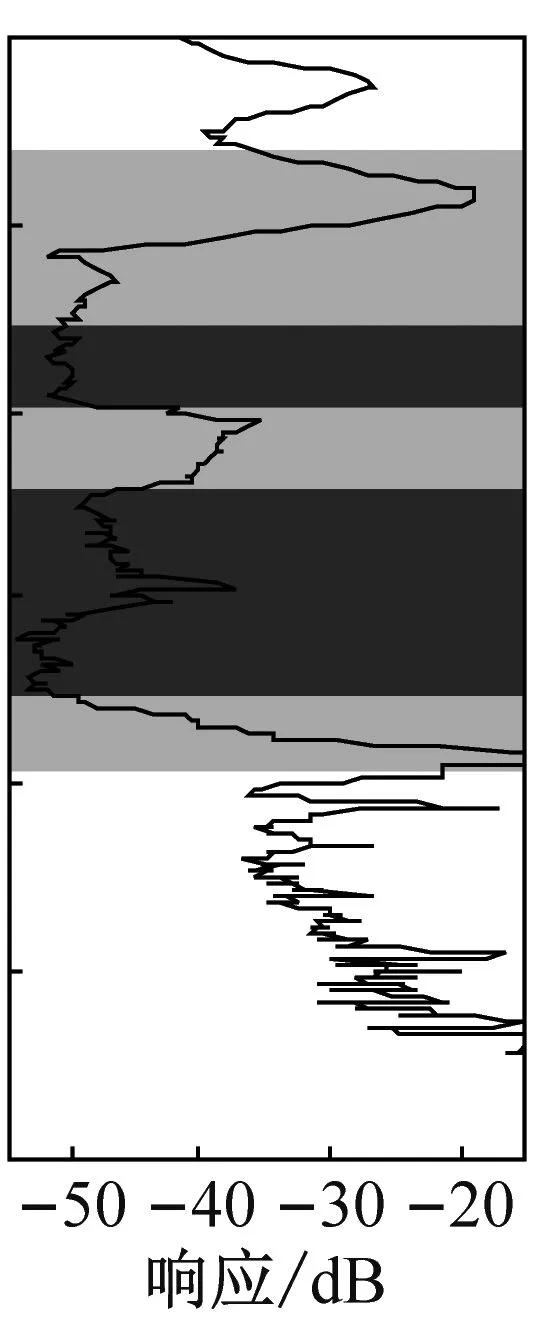
(e) 隔振器35

(f) 隔振器36

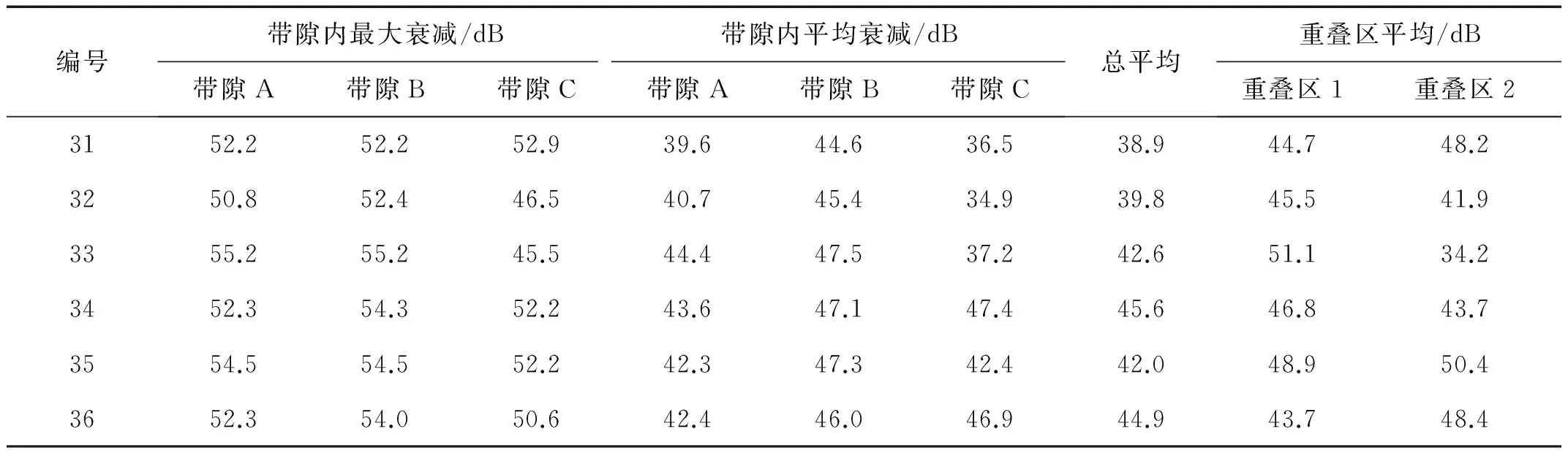
编号带隙内最大衰减/dB带隙内平均衰减/dB带隙A带隙B带隙C带隙A带隙B带隙C总平均重叠区平均/dB重叠区1重叠区23152.252.252.939.644.636.538.944.748.23250.852.446.540.745.434.939.845.541.93355.255.245.544.447.537.242.651.134.23452.354.352.243.647.147.445.646.843.73554.554.552.242.347.342.442.048.950.43652.354.050.642.446.046.944.943.748.4

3 结 论

本文在三组元凸起型声子晶体板的基础上，经过振动传递路径改进和原胞结构优化，设计了一种利用凸起板弯曲振动带隙实现单方向振动隔离的模块化的轮辐式隔振器。主要得到以下结论和成果：

(1) 经过有限元仿真对比，轮辐形凸起板的板比圆形凸起板具有更好的隔振效果，且在基板上凸起以外的空余空间开孔，可以提高弯曲带隙的终止频率，从而扩大三组元凸起型声子晶体板带宽。因此确定以带孔的凸起轮辐板为隔振器的关键部件。

(2) 分别选用了橡胶厚度和外侧凸起材料不同的3种DSPPCP原胞为轮辐板的基本单元，通过仿真和实验验证了相应的3种单轮辐板隔振器在带隙频率范围内的隔振效果。实测数据证明，单轮辐板隔振器在带隙频率范围内平均衰减幅度可以达到24 dB以上。

(3) 将以上3种DSPPCP原胞的轮辐板进行排列组合，分别获得了6种双轮辐板隔振器和6种三轮辐板隔振器。仿真及实验结果表明，在构成隔振器的各轮辐板对应带隙频率范围内振动都有明显衰减，不同轮辐板带隙重叠的频率范围的衰减幅度得到加强。双轮辐板和三轮辐板隔振器实测的带隙内平均衰减幅度分别可达34 dB以上和38 dB以上，隔振效果显著。显然，随着轮辐板数量增加(意味着振子数量增加)，其隔振器起到很好抑制振动的效果。

[1] KUSHWAHA M S, HALEVI P, MARTINEZ G, et al. Theory of acoustic band-structure of pieriodic elastic composites[J]. Physical Review B, 1994, 49(4): 2313-2322.

[2] MARTINEZ-SALA R, SANCHO J, SANCHEZ J V, et al. Sound attenuation by sculpture[J]. Nature, 1995, 378:241-245.

[3] LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736.

[4] WANG G, WEN X S, WEN J H, et al. Two-dimensional locally resonant phononic crystals with binary structures[J]. Physical Review Letters, 2004, 93(15): 154302.

[5] 祁鹏山，杜军，姜久龙，等. 新型局域共振声子晶体结构的低频带隙特性研究[J]. 人工晶体学报，2016，45(4):1094-1099.

QI Pengshan, DU Jun, JIANG Jiulong, et al. Low-frequency band gaps in phononic crystals with novel locally resonant structure[J]. Journal of Synthetic Crystals, 2016, 45(4): 1094-1099.

[6] LI L, CHEN T, WU J, et al. A discretized multi-freedom-degree model for predicting the lowest local resonant gap in phononic structures[J]. Journal of Vibration and Control, 2014, 20(11): 1727-1734.

[7] 舒海生，郜冶，张法，等. 一种局域共振型角式声子晶体梁[J]. 振动与冲击，2013，32(10):157-162.

SHU Haisheng，GAO Ye，ZHANG Fa，et al. A kind of locally resonant angle type beam of phononic crystals[J].Journal of Vibration and Shock, 2013, 32(10):157-162.

[8] LIU M, XIANG J, ZHONG Y. The band gap and transmission characteristics investigation of local resonant quaternary phononic crystals with periodic coating[J]. Applied Acoustics, 2015, 100: 10-17.

[9] ACHAOUI Y, LAUDE V, BENCHABANE S, et al. Local resonances in phononic crystals and in random arrangements of pillars on a surface[J]. Journal of Applied Physics, 2013, 114(10): 104503.

[10] POURABOLGHASEM R, KHELIF A, MOHAMMADI S, et al. Physics of band-gap formation and its evolution in the pillar-based phononic crystal structures[J]. Journal of Applied Physics, 2014, 116(1): 013514.

[11] 吴健，白晓春，肖勇，等. 一种多频局域共振型声子晶体板的低频带隙与减振特性[J]. 物理学报，2016，65(6):064602.

WU Jian, BAI Xiaochun, XIAO Yong, et al. Low frequency band gaps and vibration reduction properties of a multi-frequency locally resonant phononic plate[J]. Acta Phys. Sin., 2016, 65(6):064602.

[12] 王刚. 声子晶体局域共振带隙机理及减振特性研究[D]. 长沙: 国防科学技术大学，2005.

[13] BILAL O R, HUSSEIN M I. Trampoline metamaterial: Local resonance enhancement by springboards[J]. Applied Physics Letters, 2013, 103: 111901.

[14] HSU J C. Local resonances-induced low-frequency band gaps in two-dimensional phononic crystal slabs with periodic stepped resonators[J]. Journal of Physics D: Applied Physics, 2011, 44(5): 055401.

[15] WANG P, CHEN T N, YU K P, et al. Lamb wave band gaps in a double-sided phononic plate[J]. Journal of Applied Physics, 2013, 113(5): 053509.

[16] MA C, GUO J, LIU Y. Extending and lowing band gaps in one-dimensional phononic crystal strip with pillars and holes[J]. Journal of Physics and Chemistry of Solids, 2015, 87: 95-103.

[17] OUDICH M, LI Y, ASSOUAR B M, et al. A sonic band gap based on the locally resonant phononic plates with stubs[J]. New Journal of Physics, 2010, 12: 083049.

[18] ASSOUAR M B, OUDICH M. Enlargement of a locally resonant sonic band gap by using double-sides stubbed phononic plates[J]. Applied Physics Letters, 2012, 100(12):123506.

[19] ASSOUAR M B, SUN J H, LIN F S, et al. Hybrid phononic crystal plates for lowering and widening acoustic band gaps[J]. Ultrasonics, 2014, 54(8): 2159-2164.

[20] YU K, CHEN T, WANG X. Band gaps in the low-frequency range based on the two-dimensional phononic crystal plates composed of rubber matrix with periodic steel stubs[J]. Physica B: Condensed Matter, 2013, 416: 12-16.

Vibration characteristics of spoke-like vibration isolators with locally resonant photonic crystal plates

ZHAO Haojiang1, SONG Yang2, LIU Rongqiang3

(1. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China；2. College of Mechatronic Engineering, Northeast Forestry University, Harbin 150040, China;3. School of Mechatronic Engineering, Harbin Institute of Technology, Harbin 150001, China)

Spoke-like vibration isolators composed of three-component photonic crystal plates were designed based on the locally resonant mechanism of vibration band gaps. The low-frequency vibration isolation characteristics of the designed isolators were investigated through vibration band gap calculation, finite element simulation and tests. The results showed that compared with a round base plate, a spoke-like base plate is more effective to obtain vibration amplitude attenuation in the frequency band gap range; periodic holes on the base plate of a spoke-like pillared photonic crystal plate can enlarge the band gap width by raising the cutoff frequency of the frequency band gap. Three bilateral cells were taken as basic units of double-side pillared plates, three isolators with one spoke-like plate, six isolators with two spoke-like plates and six isolators with three spoke-like plates were designed. Test results showed that the average vibration amplitude attenuations of the designed spoke-like vibration isolators with one, two and three spoke-like double-side pillared photonic crystal plates (DSPPCPs) can reach 24 dB, 34 dB and 38 dB, respectively; these structural designs and investigation results have a potential application prospect in the field of low-frequency vibration reduction.

photonic crystal; local resonance; vibration isolator; low-frequency band gap

“111”工程(B07018)

2016-03-14 修改稿收到日期：2016-06-03

赵浩江 男，博士，助理研究员，1986年3月生

刘荣强 男，博士，教授，博士生导师，1965年10月生

TB535

A

10.13465/j.cnki.jvs.2017.15.007