Measurement of bullet impact conditions using automated in- flight photography system

Ryan Decker,Marco Duca,Shawn Spickert-Fulton

Armament Research,Design,and Engineering Center,94 Ramsey Avenue,Picatinny Arsenal,NJ,07806,USA

Measurement of bullet impact conditions using automated in- flight photography system

Ryan Decker*,Marco Duca,Shawn Spickert-Fulton

Armament Research,Design,and Engineering Center,94 Ramsey Avenue,Picatinny Arsenal,NJ,07806,USA

A R T I C L E I N F O

Article history:

18 April 2017

Accepted 21 April 2017

Available online 22 April 2017

Yaw

Terminal ballistics

Exterior ballistics

Test&evaluation

Computer vision

Image processing

Angle of attack

Knowledge of impact conditions is critical to evaluating the terminal impact performance of a projectile. For a small caliber bullet,in- flight velocity has been precisely measured for decades using detection screens,but accurately quantifying the orientation of the bullet on a target has been more challenging. This report introduces the Automated Small-Arms Photogrammetry(ASAP)analysis method used to measure,model,and predict the orientation of a small caliber bullet before reaching an impact surface. ASAP uses advanced hardware developed by Sydor Technologies to record a series of infrared digital photographs.Individual images(four orthogonal pairs)are processed using computer vision algorithms to quantify the orientation of the projectile and re-project its precise position and orientation into a three-dimensional muzzle- fixed coordinate system.An epicyclic motion model is fit to the measured data,and the epicyclic motion is extrapolated to the target location.Analysis results are fairly immediate and may be reviewed during testing.Prove-out demonstrations have shown that the impact-angle prediction capability is less than six hundredths of a degree for the 5.56 mm ball round tested.Keywords:Yaw,Terminal ballistics,Exterior ballistics,Test&evaluation,Computer vision,Image processing, Angle of attack

©2017 Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Upon impact with a target,a projectile's terminal ballistic performance is highly dependent on numerous factors including: impact velocity,bullet orientation,bullet construction,target composition,target orientation,and test geometry.The orientation of the target is easily controlled,since the target is usually stationary when testing small caliber ammunition(engraving diameter smaller than 20 mm).Bullet velocity has been measured using light-detection screens for decades which have wellestablished accuracies within 1 ft/s.The orientation of the bullet, however,is a more challenging piece of information to accurately quantify.

There are two important aspects of impactorientation that must be clari fied.The first is the angle of obliquity,which is the angular difference between the normal vector of the target surface and the velocity vector of the incoming projectile[1].For most penetratortype projectiles,penetration performance improves as the angle of obliquityapproaches zero.During testing,the angle of obliquitycan be controlled by orienting the target surface to be normal to the bullet trajectory at the impact location.

The other aspect of impact orientation to be considered is the angle of attack(AoA).The AoA is the angular difference between the projectile's velocity vector and its longitudinal axis,also known as pointing direction.During flight,the longitudinal axis of an axially-symmetric spin-stabilized projectile rotates around its velocity vector in a pro file known as epicyclic motion.This will be discussed in detail later in this report[2].When evaluating a projectile's impact effects on a target,the AoA is of particular importance because lower AoA values lead to improved penetration performance[3].

The next section of this report describes conventional methods used to measure the in- flight orientation of projectiles.The following section introduces the Automated Small-Arms Photogrammetry(ASAP)analysis method,offering an overview of the calibration procedure,computer-vision image-analysis algorithms, three-dimensional re-projection,and the process used to fit measurements to an epicyclic motion model.The following section includes sample data collected during a recent firing test.Section 4 includes a series of studies performed to evaluate the accuracy ofthe ASAP method.The final section contains the conclusions of this study.

2.Background

There are several conventional methods in use for measuring the orientation of a small-caliber bullet in flight.Yaw cards[4], which are made from plastic,paper,or cardboard-like materials are placed at various locations along a trajectory.The shape of the hole made in the card after the bullet passes through is then compared to a template to estimate the orientation angle at that location. These estimates are very crude in precision,especially for smallcaliber projectiles.The setup and post-processing of yaw cards is often exhaustive as well,as new cards are usually needed for each shot.In some situations it may not be possible to place yaw cards at the point of the impact,because damage from spalled components may affect the shape of the hole.

Another common approach involves the use of“pitch and yaw”high speed video cameras[Ref.[3]].To do this,camera systems are placed at the target location to record images of the bullet before impact.The setup of these systems along with illuminating bulbs can be exhaustive.Following a test,the results are usually analyzed byan operatorclicking onvarious points on the projectile.This type of analysis has been found to require days,(it not weeks)of data reduction,and even with proper calibration is dif ficult to verify in terms of accuracy.Because of spalling at impact,these expensive camera systems must be shielded using thick bullet-proof glass which can hinder results and further complicate setup.Sometimes, pseudo-automated image analysis software can be used to reduce the reliance on manual selection of key points[5].

Moresophisticatedmethodsoforientationmeasurement include shadowgraphs and radiographs.These images are generated by short duration pulses of light or x-rays which are similar to photographs.These images are collected between shots,digitized, and then processed relative to a template or background fiducial to develop orientation and position histories at each station.The accuracies of these systems have been reported to be within 0.14°at a given station relative to a fiducial wire,resulting in target impact accuracies between 0.24°and 0.41°[6].Some spark ranges have even better accuracies upon target impact because they may have upwards of 30 shadowgraph stations.The time required for analysis,however,can be signi ficant because of manual data collection and digitization.

Large ammunition,such as artillery and mortar projectiles,may have on-board instrumentation to measure orientation with inertial sensors or solar light detecting yawsondes[7].These systems, although accurate,are expensive and usually single-use.Such systems are much too large for use with small caliber ammunition as discussed in Ref.[5].

Finally,the Automated Launch Video Analysis(ALVA)method was developed to process high resolution moving field-of-view (FOV)videos of large caliber projectiles.This system relies on computer-vision techniques to analyze videos from orthogonal views at launch.In each video frame,the projectile shape is identi fied with sub-pixel accuracy.When the data is combined,the initial orientation history of a projectile can be measured.The accuracy of the ALVA system has been shown to be roughly 0.1°[8]. ALVA was originally designed to determine the first maximum yaw of artillery rounds,but has since been expanded to ef ficiently determine spin-rate,aerodynamic coef ficients,stability metrics, and in- flight shape transformations[9,10].

3.Automated Small-Arms Photogrammetry(ASAP)analysis

In 2014 engineers at Picatinny Arsenalpurchased a sophisticated timing system complete with illumination hardware from Sydor Technologies[11].The assembled structure of the Sydor system,which will be referred to as the“gantry,”uses lightdetection pulses from a velocity screen(located uprange of the gantry)to sequentially trigger infrared strobes as a bullet travels downrange.During these brief strobes,camera systems(Allied Vision model Prosilica GC 1380)record high resolution grayscale images of the bullet in flight.There are four stations in the current gantry system,each of which has two strobes that illuminate the FOV for two orthogonal cameras.Currently there are 4 stations (each 470 mm)apart yielding eight images(four orthogonal pairs) per shot.Illustrations and a photograph of the gantry system are shown in Fig.1.

Sample images from some of the various ammunition types tested to date are shown in Fig.2.Note the clarity of the high resolution images(1360×1032 pixels),which even show flaws in the bullet casings(caused during the engraving process during launch). The resolution,contrast,and focal length of the camera systems are more than suf ficient to accurately measure orientation as will be discussed later in this report.

At the beginning of each ammunition test,the gantry is wheeled into the firing range and aligned with the line-of- fire(LOF)using jack-stands located on the bottom of the gantry system.Once in position,the system is locked in place,and a calibration procedure is conducted before rounds can be fired.

3.1.Calibration procedure overview

The purpose of the calibration procedure is to develop the critical transforms for each camera system that relate the pixel coordinates to the range coordinate system(ℝ3).This begins with surveying the muzzle of the gun,the target,and various extrema points on the gantry system to determine their locations in ℝ3.This allows the position of each camera to be determined(relationships to surveyed gantry extrema points are known a-priori).

Fig.1.Sydor gantry system at Picatinny Arsenal.

Fig.2.Sample photographs of various ammunition types tested using ASAP.

Similarly,a calibration bar is positioned in the gantry and its extrema points are surveyed.The calibration bar contains a transparent plastic plate that appears in the field of view of each camera system.The plates contain a matrix of dots that resemble dark circles when the infrared strobes are illuminated as shown in Fig.3.Since the dot locations are known relative to the surveyed extrema points on the calibration bar(from a-priori calibration with a coordinate measurement machine accurate to 1μm),the position of each dot in ℝ3 is known as well.

At this time,calibration images are recorded for each camera. These images are processed with automated computer vision algorithms that rely on the Hough Transform analysis(for circles)to find the dots in the images[12].Since one of the dots is larger than the rest in each image,a simple sorting algorithm identi fies each individual dot.Knowledge of the ℝ3 location of each found dot and the sub-pixel coordinates of each found dot's center makes it possible to compute a transform between image coordinates(XY) and ℝ3(constrained to the plane of the calibration plate).This process automatically corrects for camera misalignment,aspect ratio skew,and some types of lens aberrations.Spherical aberrations can be corrected as well if the camera-lens systems are precalibrated(current cameras not pre-calibrated due to dif ficulty with IR illumination).The detailed calibration algorithm and matrix algebra associated with this process is included in detail in Ref.[13].

The camera setup,surveying,and calibration procedure requires as little as 30 min when completed in a team of two experienced operators of the ASAP system.Once complete,the calibration bar is removed and ammunition testing can commence.

3.2.Computer Vision analysis

When a bullet is shot through the gantry,photographs are captured that display a silhouette of the bullet shape.These images are analyzed using an adapted version of the patented ALVA method.This approach uses edge detection and morphological operations to segment the pixels corresponding to the shape of the bullet.The distribution of these pixels is then analyzed to determine the centroid,base,and nose locations,as well as the observed pitch angle(as described in Ref.[8]).The only modi fication made for ASAP is thewayinwhich the center-of-gravity(CG)is measured. Since a projectile may be yawed several degrees toward or away from the camera,it may occur that a signi ficant amount of the projectile base is visible in the photograph making it dif ficult to find an accurate measurement for the base location along the projectile axis.Fortunately,the orthogonal field of view from the supplementary camera(at that station)provides a measurement of pitch toward or away from the other camera.Thus,instead of using a simple ratio of known CG distance from the base toward the nose,a correction factorcan be used based on the amountof yaw toward or away from the camera.This allows for an even more accurate estimate of the bullet's true CG location(1-2%improvement)in image coordinates.The relationships between yaw angle toward/ away from a camera and CG location have been determined empirically using computer design models speci fic to the type of projectile being tested.The basic empirical relationship holds true for most conventional bullet shapes,but for extreme cases such as oddly shaped projectiles, finned projectiles,or stubby projectiles (9 mm bullets)this relationship should be veri fied using images from 3D computer design software.

Keypoints are identi fied in each image,and are then converted to ℝ3 coordinates using that camera's unique transform.An imaginary vector can then be drawn from the camera's focal point to the individual keypoint,possibly passing through the plane where the calibration plate had been.The final re-projected ℝ3 position of the keypoint is computed as the least-squares intersection of the two imaginary vectors from the two orthogonal cameras at that station as illustrated in Fig.4.

Fig.3.2D calibration plate(left),sample calibration image(center),and calibration dot identi fication(right).

Fig.4.Analyzed image pairs(left)and three-dimensional Re-projection of keypoints(right).

The final step in the computer vision analysis process is the determination of the projectile's orientation in ℝ3.One maychoose to estimate this value by taking the ℝ3 projection of the projectile nose and subtracting the ℝ3 projection of the projectile base or CG. However,there is a signi ficantly more accurate way to do this.This is because the position of any one keypoint along the projectile axis is only known within a distance of one pixel,which for the geometry and cameras used in ASAP is roughly 0.045 mm.The observed pitch angle in the 2D images,however,is measured based on the polar distribution of close to 100,000 pixels.Therefore, instead of subtracting two keypoints in ℝ3 to determine orientation,a more accurate algorithm is used that essentially projects the orientation vector at the CG in the 2D image into the 3D image plane.From experiment using the ALVA algorithm on computergenerated images with less than half of this resolution(number of pixels along projectile axis),the error is less than 1E-4°,which gives indication that the axial resolution(in pixels)is more than suf ficient for the Sydor Gantry system.In addition,the contrast between the projectile shape and the background has led to no observable segmentation problems to date.

To visualize the sub-pixel angle orientation(pointing direction) measurement process,consider a plane being generated in ℝ3 for each camera that contains the camera focal point,the CG keypoint, and the orientation vector.The intersection of these two planes from two supplementary cameras thus represents the orientation vector of the bullet,and is evaluated at the resolved CG location.

3.3.Epicyclic motionfitting

The bullet's resolved CG location and orientation at each of the four stations are then fit to a linearized aeroballistic model for the projectile.To do this,the bullet velocity vector must first be calculated.This is done by fitting a straight line through the four resolved CG locations in ℝ3.From experiment,this results in distance errors smaller than.04 mm which is extremely small considering the 470 mm spacing of the camera stations.

Once the velocity vector is determined in ℝ3,it is subtracted from each of the resolved orientation vectors from the four stations to determine the relative pointing direction vector,P⇀.The measured pitch and yaw values can then be calculated as

where the subscripts UP,DR,and CR correspond to the upward, downrange,and cross-range directions of the range coordinate system.It is reasonable to assume that the decrease in velocity due to drag is relatively minor in the span of flight captured within the gantry.It is also assumed that the fast and slow epicyclic oscillation rates are effectively constant within the zone of measurement.The epicyclic oscillation magnitudes,however,can either be modeled as damped or undamped.In the case of damped oscillation,the expressions that describe the expected epicyclic pitch(α)and yaw(β) as a function of range are as follows

where(x-x0)is the distance traveled,˙φF,Srepresents the fast and slow frequencies(in deg/s)of the epicylcic motion andλF,Srepresents the fast and slow damping rates(in deg/m).These values are be determined from the bullet's aerodynamic and inertial characteristics in conjuction with the bullet spin rate.Such values are usually generated using ballistics software such as PRODAS,but can also be evaluated using spark-range testing[15,16].The flight velocity(measured rom the velocity screen near the gantry)is used to determine the motion parameters from look-up data tables compiled prior to testing.The variablesKF,KSare the fast and slow mode amplitudes,which along with the angular phase shifts(φF0,φS0)are determined by minimizing the error function

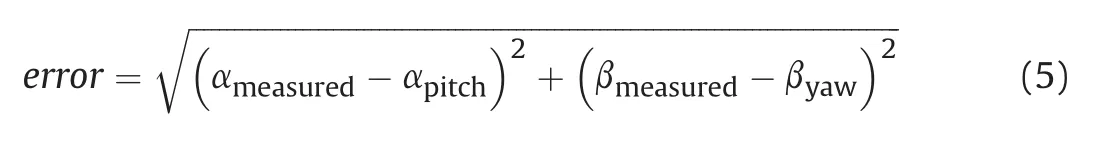
which is evaluated using any available solver.ASAP uses the“fminsearch“function of MATLAB[17].To improve the chances of quickly determining an accurate solution,the initial conditions forKF,Sand φF0,S0are determined using an approach similar to the one suggested by Ref.[14]and is discussed in detail in Ref.[13].Once the error function is minimized,the impact conditions are easily calculated by extrapolating Eq.(3)and Eq.(4)to point of impact.

With suitable initial guesses,the fitting process is robust.For most shots,it requires just a few seconds to find optimal values for the four variables to within four signi ficant digits of precision. Sample results from a recent firing of an M855A1 5.56 mm bullet (September 2016)are shown in Fig.5.For the data shown,the gantry was positioned only 2.5 m from the weapon muzzle,which has the effect of illustrating the nutational(slow epicyclic oscillation)motion before it damps out.

4.Assessment of accuracy

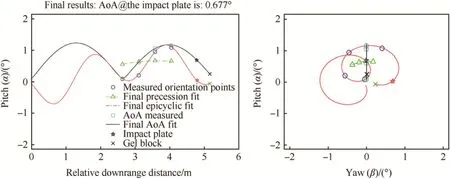
Fig.5.Sample Results from ASAP Output(M855A1 fired September 2016).Pitch Motion Versus Downrange Distance(left)Alpha-Beta Plot(Right).

Quantifying the accuracy of the ASAP system is not a straightforward process.It is made especially dif ficult because the accuracy of the system is believed to be signi ficantly better than any other conventional method available at Picatinny Arsenal's Armament Technology Facility.From experiment,each time a round is fired, the measured motion visually appears to follow right-handed epicyclic motion,as expected.There are other obvious indicators that also suggest the algorithm is working correctly,such as the reprojected length between the nose and the base matching the known projectile length to 0.2 mm at each station,and the velocity pro file results in a straight line,with slight deviations less than 1 mm,but always in the direction of the orientation vector(which is expected due to lift known as epicyclic swerve).These deviations correlate to worst-case errors in angle of obliquity measurements smaller than 0.02°.

Additional sources error for measuring AoA must be identi fied and assessed as well.Possible errors come from a variety of sources including improper calibration measurements,round-to-round variation from a baseline aeroballistic model,and even the asymmetric geometry of the bullets themselves.This section will assess the error of the system using several approaches.

4.1.Theoretical orientation error measurement

In addition to the sources of error already listed,there is rounding and estimation error introduced within the ASAP software.Before results are computed,there are a number of leastsquares-type fits that are used in the calibration and survey processes.In addition,resolving the keypoints into ℝ3 involves a linear least-squares fit of the two projection vectors.Finally,the velocity vector is a least-squares fit of the resolved CG position history,and the epicyclic motion model is a numerically driven steepestdescent fit,which is never a perfect match to the measured data. These least-squares-type fits mainlyserve to“smooth”the data,but may introduce error as well.

Therefore,to assess the accuracy of the ASAP's ability to predict impact conditions,the accuracy at each station must first be investigated.To do this,the error in the linear least-squares solution between the two CG re-projection errors is examined.From all shots analyzed using the current version of ASAP,the largest leastsquares error encountered was roughly 0.023 mm.However,closer examination has shown that almost 95%of this error is in the downrange direction,with less than 5%of this error occurring in the transverse(up and cross-range)directions.This was puzzling at first,until it was realized that this error is almost entirely due tothe process of determining where a keypoint is located along the projectile axis in the 2D image.As stated earlier this report,the accuracy of measuring the orientation of the segmented bullet shape in each photograph is orders of magnitude more accurate that the determination of the CG,nose,or base position along the projectile's axis,so although the location of the projectile axis vector can be determined with incredible precision,the keypoint locations along that axis can only be determined within roughly one pixel.Therefore,it makes sense that almost all of the reprojection error is in the downrange direction,and makes even more sense that the magnitude of this error is roughly half of the worst-case pixel size(0.045 mm).Since the spacing between the stations for these experiments was 470 mm,the CG projection error in the downrange direction is virtually negligible when fitting the velocity vector.

The projection errors in the transverse directions,however,are important because they contribute to errors in the orientation angle measurement.As described in the previous section,instead of using the projected nose and CG locations in ℝ3 to measure the orientation vector,it is instead computed as the intersection between the planes containing the re-projected CG position,the 2D orientation vector(on the calibration plane)and the camera focal point.This can also be accomplished by projecting an additional“heading”keypoint that is one pixel from the CG in the direction of the 2D orientation measurement in the image.Since this heading keypoint is based on the CG position along the projectile axis,the re-projection errors in the axial direction are the same,and only the difference in the transverse projection errors remain.

When this“heading keypoint”approach is conducted,the largest maximum possible angle error(from the least-squares reprojection error in all directions)was 0.08°.Since we know that at this resolution the image processing algorithm has a demonstrated accuracy that is better than 0.001°error(per degree of pitch angle) [Ref.[8]]for images with less than half of the resolution(pixels along projectile axis)generated using the Sydor gantry,it is assumed that the digital photo quality is suf ficient and the vast majority of the error is present in the re-projection transform which is established during the surveying process.The problem originates from using long-distance measurement equipment to survey the gantry and calibration bar.This equipment(Sokkia CX-102),reports a measurement error of 0.0006°in the horizontalazimuth and zenith-angle directions,and a length measurement precision of 1.52 mm.When converted to the range coordinate system(which is measured from roughly 4 m away),this precision corresponds to an error in the downrange direction of approximately 1.50 mm and errors in the cross-range and up directions of 0.022 mm.Perturbing the survey measurements by these amounts has been found to impart roughly 0.05°of error into the pitch and yaw measurements at a given station for the same set of input images.

Improvements to the survey procedure are in progress that include surveying more reference extrema points to further reduce calibration errors.Since sub-millimeter calibration is desired,efforts are underway to replace the current two-stage surveying procedure with one in which calibration plates face all cameras at once.This will eliminate the possibility of gantry movement between the calibrations of supplementary cameras.

4.2.Comparison to manual high speed camera analysis

In September of 2016,a test was conducted at Picatinny Arsenal in which a sequence of 5.56 mm rounds were fired at various impact targets.During those tests,conventional pitch and yaw analysis was manually conducted for all rounds in which quality high-speed video was collected of the target impact(which required many days to process).

The ASAP results are relatively close to the conventional analysis,as the methods had an average disagreement of 0.20°with a standard deviation of 0.73°.This disagreement may seem large, however this is expected because the precision of the conventional analysis is believed to be 1.9°[Ref.[3]]for the best-case achievable resolution of the high speed cameras(30 pixels).This serves only has a crude veri fication that ASAP is making correct measurements, but shows de finitively that fixed-view high speed video analysis is insuf ficient for characterizing bullet impact angle,unless a drastic improvement in axial resolution is possible.Therefore,to further assess the accuracy of the ASAP method,more involved analyses are necessary.

4.3.Measurement sensitivity and extrapolation study

The ultimate purpose of ASAP analysis is to estimate the impact angle upon a downrange target.Testing with the Sydor system involves a variety of targets,some of which need to be placed more than one meter beyond the gantry to prevent damage to the equipment.As the target is placed farther from the gantry,the ability of ASAP to accurately predict the impact conditions quickly diminishes.Since the AoA can change many degrees in only one meterof travel,it is important to position the gantry relativelyclose to the impact point.

An in-depth Monte-Carlo-type simulation study was conducted to evaluate the sensitivity of station angle errors and how they correlate to predicted impact conditions at distances of 0.1 m, 0.5 m,1.0 m,and 2.0 m beyond the last gantry station.To do this, two nominal epicyclic trajectories were generated,one with relatively large values of total AoA(6.0°)and one with relatively small values of total AoA(2.0°).The expected pitch and yaw values ateach station were determined based on these nominal trajectories.In each iteration of the simulation,the true values of pitch and yaw at each station were perturbed by small errors ranging from±0.08°in increments of 0.01°.In total,40,320 combinations of possible perturbations were examined.The worst impact angle result of any of these combinations resulted in a difference between the predicted AoA and the nominal AoA of 0.135°.Interestingly,the results for both the high and low AoA trajectories were so similar that the data was nearly a perfect overlap,suggesting that the angle of attack predictions at impact are not overly sensitive to the magnitude of the initial motion.The standard deviation of these errors at each target extrapolation distances were also calculated.The largest standard deviation(of these distances)was found to be less than 0.06°at the target as shown in Fig.6.

4.4.Omitted-pair study

A final study was also conducted,where experimental orientation measurements from three stations was used to predict the orientation at the fourth(omitted)station.This was done in many iterations,allowing each station to be the omitted data point.From this analysis,the error in the AoA prediction at the fourth station averaged roughly 0.22°.This result suggests that the algorithm is working,but also demonstrates that only utilizing three stations worth of data introduces error in the aeroballistic fitting process. Since the results seem to be much better using all four stations,the one-sigma value from the measurement disturbance and extrapolation study has been adopted to best-represent the demonstrated accuracy of the system.

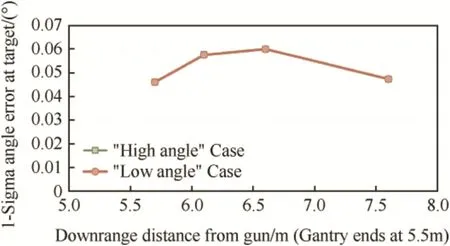
Fig.6.Results from Angle Measurement Sensitivity Study(results overlap).

5.Conclusions

The ASAP analysis method is considerably faster than any other testing method available.This also makes it a low-cost option for small-caliber ammunition testing,especially compared to other methods that require extensive manual setup and post-processing. The automated nature of the analysis allows results to be evaluated on site within moments of firing.As demonstrated,the precise calibration technique and sophisticated computer vision algorithms can estimate the AoA on target to an accuracy of 0.06.°Angle of obliquity measurements are even more accurate,as they are simply the slope of the velocity line(assuming the target face is orthogonal to the downrange direction).

The modular nature of the ASAP/Sydor system combined with the expandability of the software,will eventually allow multiple gantries to be used together.The possibility of capturing multiple images of a bullet from each camera station is also being investigated.The ASAP algorithms currently rely onpreviouslyestablished aerodynamic and inertial characterization of the ammunition. However,increasing the number of measurement stations(or doubling the number of data points collected at each station)will eventually allow the complete aerodynamic characterization of new experimental ammunition that can be conducted on site in a precise and completely automated manner.

[1]Carlucci D,Jacobson S.Ballistics:theory and design of guns and ammunition. Boca Raton,FL:CRC Press;2008.

[2]McCoy R.Modern exterior ballistics:the Launch and flight dynamics of symmetric projectiles.Atglen,PA:Schiffer Publishing;1999.

[3]Minisi M,Spickert-Fulton S.Angle of attack at impact and its effects on terminal effects testing.Picatinny Arsenal,NJ:U.S.Army Armament Research, Development,and Engineering Center;January 2004.

[4]Use of yaw cards during projectile development,2010.South Burlington,VT: Arrow Tech Associates,INC.;Jul.2010.White Paper.

[5]Decker R.A computer vision-based method for artillery characterization. Doctoral Dissertation.Monterey,CA:Naval Postgraduate School;December 2013.

[6]Ehlers T,Guidos B,Webb D.Small-caliber projectile target impact angle determined from close proximity radiographs.Aberdeen Proving Ground,MD: Army Research Laboratory;Oct.2006.ARL-TR-3943.

[7]Davis B,Guidos B,Harkins T.Complementary roles of spark range and onboard free- flight measurements for projectile development.Aberdeen Proving Ground,MD:Army Research Laboratory;Aug.2009.ARL-TR-4910.

[8]Decker R,Kolsch M,Yakimenko O.An automated method for computer vision analysis of cannon-launched artillery video.ASTM J Test Eval December 2013;42(No.5).

[9]Decker R,Kolsch M,Yakimenko O.An automated method for computer vision analysis of cannon-launched artillery video.ASTM J Test Eval December2013;42(No.5).

[10]Decker R,Duca M,Hooke R.Aerodynamic coef ficient measurement using Launch video analysis of sabot-equipped projectiles.In:Proceedings of the 2014 joint classi fied bombs/warheads&ballistics symposium.Monterey,CA: NDIA;August 2014.

[11]Sydor Technologies.Sabre Ballistics.http://sydortechnologies.com/ballisticimpact-testing/external-ballistics/.Accessed December 2016.

[12]Hough PVC.Machine analysis of bubble chamber pictures.In:Proceedings of the international conference of high energy accelerators and instrumentation; 1959.

[13]Decker R,Duca M,Fischer C,Neira H,Spickert-Fulton S,Schaarschmidt K. Automated small-arms Photogrammetry(ASAP)method for measurement of bullet impact conditions.Picatinny Arsenal,NJ:U.S.ArmyArmament Research,Development,and Engineering Center;February 2016[in editting].

[14]Ehlers T.Selecting the spacing of close proximity radiographs to determine the angle of attack at target impact.Aberdeen Proving Ground,MD:Army Research Laboratory.ARL-TR-4180;July 2007.

[15]Prodas software.South Burlington,VT:Arrow Tech Associates;1999.V3.

[16]Guidos B.“Aerodynamics of denel 105mm XM2019 projectile obtained from spark range firings,”ARL-TR-5187.Aberdeen Proving Ground,MD:Army Research Laboratory;July 2004.

[17]MATLAB.Natick,Massachusetts:The MathWorks Inc;2011.

11 January 2017

*Corresponding author.

E-mail address:Ryan.j.decker6.civ@mail.mil(R.Decker).

Peer review under responsibility of China Ordnance Society.

http://dx.doi.org/10.1016/j.dt.2017.04.004

2214-9147/©2017 Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

in revised form