基于Agent建模的计算实验金融学：思想与方法

(杭州电子科技大学经济学院，浙江 杭州 310018)

基于Agent建模的计算实验金融学：思想与方法

梁容佳袁桂秋

(杭州电子科技大学经济学院，浙江 杭州 310018)

本文首先阐述了复杂自适应系统CAS的内涵，因为资本市场是一个复杂自适应系统，所以引出基于CAS理论的计算实验金融学。其次介绍了计算实验金融学的建模框架和建模思路，强调了市场价格形成机制、Agent个体行为和市场信息结构三者之间的相互作用。最后阐述计算实验金融学的发展前景，为计算实验金融学的进一步研究提供参考。

计算实验金融学；复杂自适应；Agent个体；非理性行为

一、引言

建立在理性投资者和市场效率假说基础之上的经典金融理论认为，投资者都是理性的，都能根据市场信息理性的做出决策，任何人都无法获得超额收益，所以，市场是有效的，市场价格能完全反映所有可用信息(Fama，1970)。但事实上，金融市场出现一些如股票过度波动、“日历效应”、网络泡沫和羊群效应等异象(Financial Anomalies)。这些现象不能被经典金融理论解释，由此引发了人们对经典理论能否有效解释金融市场提出疑问。赵尚梅，孙桂平，杨海军(2015)指出经典金融理论由于其假设和研究方法的局限，在解决市场异象这些问题上陷入了前所未有的挑战。诸多“新金融”理论应运而生，制度金融学NIF(New Institutional Finance)放松了原有的有效市场“无摩擦”的假设并研究交易成本和交易制度的演进；行为金融学BF(Behavioral Finance)则放松了完全理性人的假设，引入个体偏好和心理偏差等因素，构建基于有限理性个体的资产定价模型(张维等，2013)。虽然这些理论解释了一些市场异象(如过度反应、羊群效应等)，但是这些理论仍然存在数理建模复杂、数据获取难度高、人工投入及计算成本高等缺陷，这些缺陷限制金融理论的发展，导致目前金融经济学对一些复杂的市场异象(如金融危机)仍难以进行较全面的解释。基于Agent计算实验金融学ACF(Agent-based Computational Finance)结合计算机高效的计算能力和快速处理信息的能力为处理复杂问题提供了快捷的操作工具，其使复杂建模具有可操作性，同时其不需要获取具体的微观数据进行实证检验，只需在建立的人工市场模型中改变相关参数模拟真实市场亦可得到所需结果，在一定程度上弥补了目前金融学理论研究存在的一些缺陷。如Hongquan Li、Mengyun Tang、Wei Shang和Shouyang Wang(2013)通过建立异质Agent的计算实验金融学的框架得出适度的证券交易税可降低市场波动，但对市场效率产生不良影响，因此建议监管者应谨慎引进证券交易税以求在市场稳定性和效率性中取得平衡。计算实验方法成为了与“实验”、“实证”和“数理分析”并驾齐驱的“第四种”科学研究手段(张维等，2013)，成为探究复杂经济系统研究的新方法，引起了众多经济学家的关注并开始采用计算实验方法研究金融问题。

本文通过介绍与经典金融理论研究思想不同的复杂自适应系统思想，并引出计算实验金融学，在复杂自适应系统思想上建立起来的一门金融学分支。通过介绍国内外学者所著文献，总结目前国内外学者对计算实验金融学的研究成果，介绍一些具有代表性的理论模型，并分析计算实验金融学的发展前景，为以后计算实验金融学的发展提供研究方向。

二、复杂自适应系统CAS

Santa Fe研究所提出了“复杂自适应系统CAS(Complex Adaptive System)”的概念，认为系统的复杂性是由系统中主体性元素适应环境的结果(Holland，2001)，其中就点出了“适应性造就复杂性”这个CAS理论的核心思想。关于复杂自适应系统CAS，至今没有一个标准的定义，众多学者对其进行阐述。CAS系统通常被定义为由众多“Agent”组成，这些“Agent”可以是细胞、个人、公司和项目，这些个体(Agent)行动相似且连续，并能对其他个体(Agents)的行为做出反应(Holland，1995)。随着众多学者对CAS研究的不断加深，CAS的定义更加清晰明确。CAS是一个由大量独立的个体构成的系统，这些个体以独立自主、非线性的方式局部产生相互影响，并通过完全不确定性、不规则且不会被一些中心化或者整体性机制影响的交互作用体现自组织机制，在大范围内适应自发行为，这种行为的观察具有不可预测性(Robert Abbott，MirsadHad ikadi，2017)。这也就是说复杂自适应系统具有不确定性、不可预测性、非线性等特点，系统中的个体具有适应性，他们能够与其他个体进行交互作用，其中强调了个体的主动性、自组织性与积极性。众多个体每个时刻做出的大量决策决定了这个系统的总体行为状况。在这种系统中的过程同样需要自适应，我们称它们为复杂自适应过程(I. T. Hawryszkiewycz，2009)。由于个体与其他个体、环境之间持续进行交互作用，不断“学习”和“积累经验”，逐步调整自己的决策，导致宏观系统在这些具有适应性的微观个体影响下出现分化并逐渐聚合而成新的系统。

理解复杂自适应系统理论非常重要，资本市场就是一个复杂的自适应系统，这为资本市场提供一个新的内涵。有些学者通过探讨资本市场价格的形成机制，如在股票市场中探究影响股价波动的因素，找出价格形成规律。如王朝晖和李心丹(2015)采用基于Agent的计算实验金融方法，引入连续竞价机制，建立仿真技术探究股票市场的“波动性之谜”，得出交易者个体的从众行为是市场总体过度波动原因的结论。资本市场本身具有较强的复杂性，CAS系统认为资本市场是由多种多样的投资者(Agent)组成，而这些投资者具有一定的适应性，这体现在投资者(Agent)与投资者(Agent)之间以及投资者(Agent)与环境之间，个体投资者能与其他投资者和环境产生交互作用。这些投资者(Agent)能够适应其他投资者(Agent)的行为及环境约束(张维等，2003)。投资者之间是相互影响的，在不具备完全信息的市场情况下，当资本市场报出一个价格，投资者针对市场价格形成不同的预期并采取不同的决策形成各自的报价，从而影响市场进一步形成新的市场价格，而新的市场价格又进一步影响投资者决策，投资者参照新的市场价格和其他投资者的决策形成新的预期，从而影响自身的决策。由此可见，CAS理论认为资本市场价格的形成是由各个投资者相互影响不断改进决策决定的，投资者表现出的适应性决策与市场变化是协同进化的。这与传统金融思想理论不同，其指出市场的宏观变化由宏观政策影响，进而影响个体，其将资本市场复杂性归结于外界随机因素影响；而CAS系统强调投资者的主动性，其指出市场的宏观变化由这些适应性的个体造成，由个体的决策影响宏观市场，宏观层面复杂性由个体适应环境产生。由此可见，经典金融思想主要依据“自上而下”的研究方法，复杂自适应系统主要是“自底而上”的方法，其注重从个体着手分析，探究其对宏观系统产生的影响。计算实验金融学(ACF)正是建立在资本市场是复杂自适应系统的基础上进行研究，并采用“自底而上”的建模思路探究实际金融市场的规律。

三、计算实验金融学建模方法

计算实验金融学ACF是将金融市场视为包含多个异质主体的系统，应用信息技术来模拟实际金融市场(如股票市场、外汇市场、期货市场等)，在既定的市场结构下，通过市场微观层次Agent的行为来解释市场动态特性及其成因的一门金融学分支(张维等，2012)。最早期的模型是Agent个体演化模型，最为典型的是Santa Fe研究所提出的人工股票市场模型(W.B.Arthur，J.H.Holland，B.LeBaron等，1997)。随着计算实验金融学的发展，计算实验金融学的建模类型由Agent个体建模类型向复杂交互网络发展，Agent也逐渐具有“学习”能力和预期决策能力。张维、李悦雷和熊熊等(2012)经过文献总结将目前建模类型总结为价格形成机制建模、Agent个体行为建模和市场信息结构与交互模式建模三个方面，如下图所示：

图1 计算实验金融学的建模方法

以YosraMefteh Rekik、WafikHachicha、YounesBoujelbene(2014)的建模方法为例，主要包括以下几个步骤：

(1)市场环境：

一般是所有交易都按固定价格执行，投资者的报价都能进行交易，为了促进交易的完成，通常建立做市商制度，促使买卖双方交易均能达成，不存在无法交易的现象。在这里，YosraMefteh Rekik、WafikHachicha、YounesBoujelbene等人是选择了瓦尔拉斯拍卖制度，遵守交易者的需求函数，调整价格平衡市场总供给与总需求。

(2)交易者模型：

相当于投资者决策模型，市场参与者根据预期调整自己的资产组合比例。一般假定模型中的投资者符合常数绝对风险厌恶CARA(constant absolute riskaversion)模型，投资者的目的是期望效益最大化，而投资者相对风险厌恶随着财富的增加而增加，每个投资者都有一个CARA效用函数。为了简化模型降低难度，通常假定市场中有两种资产，一种资产是风险资产如股票，收益包括资本利得和股息收益率；一种是无风险资产，收益率为rf，投资者两种资产持有量总和为1。

令效用函数为U(Wi,t+1)=-e-γWi,t+1

①

其中，为绝对风险厌恶系数，Wi,t+1为投资者i在t+1刻的财富总值。

当①式最大化时，投资收益率满足正态分布，得风险效用函数为

②

E(Wi,t+1)=Xi,t(Pt+1+dt+1)+(1+rf)(Wi,t-PtXi,t)

③

其中，Xi,t是投资者i在t期的风险资产持有量，Pt+1+dt+1是投资者i在t期对t+1期风险资产价值与股息收益水平的期望值，是投资者t+1时刻的财富水平。Wi,t是投资者i在期初用于投资的财富，Pt是风险资产在t期市场的均衡价格水平。

由于对应一种无风险资产和一种风险资产，总风险由风险资产风险和权重决定，得

④

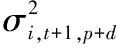
⑤

当效用函数U达到最大值时，即求Umax.对(5)式求导，即U′=0。

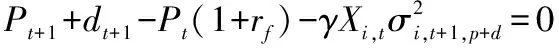
⑥

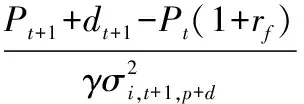
⑦

由此，不同投资者可以根据自己对未来风险资产价值与收益预期和风险估计调整自己风险资产的比例，从而改变自身决策。

(3)投资者行为模型：

针对不同行为的投资者设定不同模型，这些不同行为的投资者包括基本面交易者(Fundamentalists)、噪音交易者(noise traders)、风险厌恶性投资者(Loss-averse investors)等。在实际实验中可通过赋予投资者一定的“学习”能力和调整“风险规避系数”对投资者进行分析(赵尚梅，孙桂平，杨海军，2015)。

四、计算实验金融学的发展前景

基于Agent的计算实验金融学是在复杂系统范式的视角下，研究市场动态的基本特性。计算实验金融学运用计算机技术进行建模，放松了完全理性人的假设，使建立的模型更接近于真实金融市场。在一定假设条件下，研究者可以采取以上建模思路并设置相关参数，根据特定的经济现象建立相应的人工金融市场模型来探究相关经济问题，它的发展主要在一下几方面：

(1)股票市场、外汇市场及银行领域的研究仍为主流，而衍生品市场及保险市场等也会引起学者研究。张维等(2012)通过中国学术期刊网(CNKI)和美国科学信息研究所(ISI)的“科学引文索引(SCI)”和“社会科学引文索引(SSCI)”的数据库检索出大多数国内外学者运用计算实验方法研究股票市场，其次是对银行的研究，而对保险、债券、基金、衍生品等研究。这领域在近年来仍将是主流，随着计算技术的提高，学者对市场的解读更加深刻，衍生品市场、保险市场等领域的研究也会逐渐展开。

(2)为研究市场动态提供仿真平台，推动金融领域发展。计算实验金融学为研究复杂真实市场提供仿真平台，为现代金融学理论提供工具。由于数理建模较为复杂，计算实验金融学方法为研究复杂金融现象带来了希望。袁建辉、邓蕊和曹广喜(2011)借助行为金融理论，基于异质性，运用计算实验金融方法得出投资者的模仿可作为羊群行为形成的一种机制，其对股票价格波动存在明显影响。由此通过研究微观层次Agent来解释市场动态，完善一些理论研究，推动金融领域发展。

(3)运用计算实验金融方法为我国的金融监管提供决策。我国资本市场发展不够完善，相关监管措施还不够健全，真实市场内幕交易、市场操纵现象频频发生。目前金融创新产品不断出现，互联网金融飞速发展，市场创新中直接融资市场和理财产品逐渐兴起，而我国相关监管措施还未跟上相应步伐，市场风险加大，资本市场的正常运行受到威胁，因此研究中国资本市场的规范化和制度建设成为关注问题。监管者可以通过运用计算实验金融方法建立人工市场仿真平台对真实市场进行模拟，得出监管措施。曾薇(2013)通过构建我国连续双向拍卖人工股票期权市场仿真实验平台，得出限仓额度的大小不会对市场价格造成显著影响，但对市场成交量造成影响，进而指出我国股票期权市场可以通过对限仓额度的灵活调整来规避由持仓量过于集中而可能引发的市场操纵行为。

(4)神经网络与模糊逻辑、遗传算法等有效融合实现投资者决策进化的方法将盛行。为实现投资者的决策进化机制，提供信息处理功能，运用神经网络模仿人脑的决策机制，将不仅仅运用实验金融学研究，在计算领领域、物理学领域也将受到推崇。为实现agent决策的进化体现各个agent的学习行为，将神经网络与模糊逻辑、遗传算法进行实验研究成为计算实验金融学学者的选择。

[1] Fama，E. Efficient Capital Markets：A Review of Theory and Empirical Work[J]. The Journal of Finance，1970，25(2)：383-417.

[2] 赵尚梅.孙桂平.杨海军.股票期权对股票市场的波动性分析：基于agent的计算实验金融仿真角度[J].管理工程学报，2015，(1)：207-215.

[3] 张维.武自强.张永杰.熊熊.冯绪.基于复杂金融系统视角的计算实验金融：进展与展望[J].管理科学学报，2013，(6)：85-94.

[4] Hongquan Li.Mengyun Tang. Wei Shang. Shouyang Wang. Securities Transaction Tax and Stock Market Behavior in an Agent-based Financial Market Model[J]. Procedia Computer Science，2013，(18)：1764-1773.

[5] Holland，J. Modeling Complex Adaptive System[M].2001.

[6] Holland，J. Hidden order：How adaption builds complexity[J]. Cambridge Perseus Books，Leonardo，1995，(29)：3.

[7] Robert Abbot，MirsadHad ikadi. Complex Adaptive Systems，Systems Thinking，and Agent-Based Modeling[J].Advanced Technologies，Systems，and Applications，2017：1-8.

[8] I. T. Hawryszkiewycz. Modeling Complex Adaptive Systems. Information Systems：Modeling，Development，and Integration. 2009，(20)：458-468.

[9] 王朝晖.李心丹.从众行为与“波动性之谜”[J].宏观经济研究，2015，(4)：80-89.

[10] 张维.刘文财.王启文.刘豹.面向资本市场复杂性建模：基于Agent计算实验金融学[J].现代财经，2003，(1)：3-7.

[11] 张维.李悦雷.熊熊.张永杰.张小涛.计算实验金融的思想基础与研究范式[J].系统工程理论与实践，2012，(3)：495-507.

[12] Arthur W B . Holland J H. LeBamn B，et al. Asset pricing under endogenous expectations in an artificial stockmarket[C].Arthur W B，Durlauf S，LANE D，eds. The Economy as an Evolving Complex System II. Reading，M A：Addison-Wesley . 1997.

[13] YosraMefteh Rekik.WafikHachicha.YounesBoujelbene. Agent-Based Modeling and Investors’ Behavior Explanationof Asset Price Dynamics on Artificial Financial Markets[J]. Procedia Economics and Finance，2014，(13)：30 - 46.

[14] 袁建辉.邓蕊.曹广喜.模仿式羊群行为的计算实验[J]. 系统工程理论与实践，2011，(5)：855-862.

[15] 曾薇.我国股票期权市场计算实验金融仿真研究[J].华东经济管理，2013，(2)：72-75.