支持向量机方法在温度预报中的应用——以沈阳地区为例

鲁杨，李典，王雪萌，吴宇童，柴晓玲，班伟龙，张治

（1.沈阳市气象局；2.沈阳市沈北新区气象局，辽宁沈阳110000）

支持向量机方法在温度预报中的应用
——以沈阳地区为例

鲁杨1，李典1，王雪萌2，吴宇童1，柴晓玲1，班伟龙1，张治1

（1.沈阳市气象局；2.沈阳市沈北新区气象局，辽宁沈阳110000）

本文利用沈阳站温度资料和东北中尺度数值模式预报场资料，采用K-means算法进行季节划分试验，基于支持向量机方法（Support Vector Machine，简称SVM）进行交叉验证和预报检验，试图建立温度季节预报模型。结果表明：聚类季节划分与传统季节划分之间存在差异，传统的春、秋两季被划分为不连续的两类，传统的夏、冬两季被划分的不明显，仅在时间长度上有所差异；支持向量机方法对夏季温度预报准确率最高，各时次温度误差≤2℃的准确率平均为81.2%。冬季温度预报准确率最低，各时次温度误差≤2℃的准确率平均为69.2%。冬季客观方法对夜间降温幅度的预报能力存在不足，而春季客观方法对夜间最低气温的预报能力存在不足。平均绝对误差除个别时次超过2℃外，其他时次均在误差范围内，客观预报方法是可用的。

支持向量机方法；聚类分析；季节划分

沈阳市位于辽河平原中部，受季风影响较大，属于北温带受季风影响的半湿润大陆性气候，全年温差较大，四季分明。夏季热而多雨，冬季寒冷漫长，春秋两季温度变化迅速。随着科技的进步和社会的发展，农业和各种重大活动对气象服务的需求日益增高，温度的精细化预报成为目前天气预报面临的挑战与问题。大气环流的变化存在复杂性和非线性，温度的变化与各种预报因子间存在非线性相关，支持向量机（Support Vector Machine，简称SVM）方法是处理非线性分类和回归等问题的一种有效的方法。近年来，多地气象部门利用模式直接输出产品，应用SVM方法制作各种气象要素预报，取得了一定成果。冯汉中[1]等利用1998年～2000年9～11月T106模式36小时预报的各种输出产品构造因子，以单站有无降水为预报对象，采用MOS法方式构造样本，通过建立单站的晴雨SVM分类预报模型,利用1990年～2000年4～9月ECMWF北半球的500hPa高度、850hPa温度、地面气压的0小时分析场资料，确定关键区域，构造预报因子，以PP法方式构造样本，通过训练建立了四川盆地内单站气温的SVM回归预报模型，并进行了模拟试验，结果表明无论是单站晴雨的SVM分类预报模型还是单站平均气温的SVM回归预报模型都显示出了良好的预报能力。高永娜[2]等以风向、风速、云量、相对湿度、露点温度、气压6个相关因素为因子，采用Libsvm软件进行预测建模，用真实数据进行分析对比，得出SVM方法预测气温数据与真实数据有较高的拟合度。王在文[3]等利用北京市气象局中尺度业务模式（MM5V3）的数值预报产品和观测资料，制作北京15个奥运场馆站点6～48小时逐3小时的气象要素释用产品，对比MM5V3模式，2米温度的均方根误差减小12．1%，与同期MOS方法预报结果相对，2米温度预报效果SVM略优于MOS。

本文采用K-means算法进行季节划分试验，在东北中尺度数值模式WRF-3KM直接输出产品的基础上，基于支持向量机方法，进行交叉验证和预报检验，建立本地区的温度预报的季节模型，为农业生产及大城市精细化预报业务提供保障。

1 资料与方法

1.1 资料

本文所用资料为沈阳站（站号：54342）历史同期（1980年～2010年）温度资料，2013年～2014年东北中尺度数值模式WRF-3KM未来12～36小时预报场资料和沈阳国家观测站实况资料。

1.2 方法

1.2.1 SVM方法 为解决基于数据的非线性建模问题，基于V．N．Vapnik等提出的统计学习理论（小样本理论）[4-8]，近年来提出了支持向量机（Support Vector Machines，简称SVM，下同）方法[9-10]，其基本思路为：以结构风险最小化为前提，定义最优化线性超平面，把寻找最优线性超平面的算法归结为求解一个凸规划问题，从理论上得到的局部最优解，也就是全局的最优解；进而基于Mercer核展开定理，通过非线性映射，把样本空间映射到一个高维乃至于无穷维的特征空间，使在特征空间中可以应用线性学习机的方法，解决样本空间中的非线性分类和回归的问题。本文通过回归问题预报温度。

回归分析又称函数估计，其解决的问题是：根据给定的样本集｛（xi，yi）｝|i=1，…，k｝，其中xi为预报因子值，yi为预报对象值，寻求一个反映样本数据的最优（按某一规定的误差函数计算，所得函数关系对样本数据集拟合的“最好”）函数关系y=f（x）。

1.2.2 K-means算法 K-means算法[11-12]为经典的基于划分的聚类方法，是十大经典数据挖掘算法之一。其基本思想是：随机选择K个对象，每个对象代表一个簇的初始均值，也称初始类中心，对剩余的每个对象，根据其与各个簇均值的距离，将其指派到最相似的簇。然后计算每个簇的新均值，这个过程不断的重复，直到准则函数收敛。本文采用K-means算法进行季节划分试验，K值为4。

2 季节划分

采用02时、08时、14时和20时的沈阳站历史同期资料，对4个时次进行年平均处理，采用K-means方法，进行聚类划分，按传统的春、夏、秋、冬4季，将所有样本数划分为4类，结果如图1。从图中可以看出，聚类分析后，将具有相同变化趋势的样本划分为一类，与传统季节划分方式存在差异，将传统的春、秋两季划分为不连续的两类，而传统的夏、冬两季划分的变化不明显，仅在时间长度上有所差异。

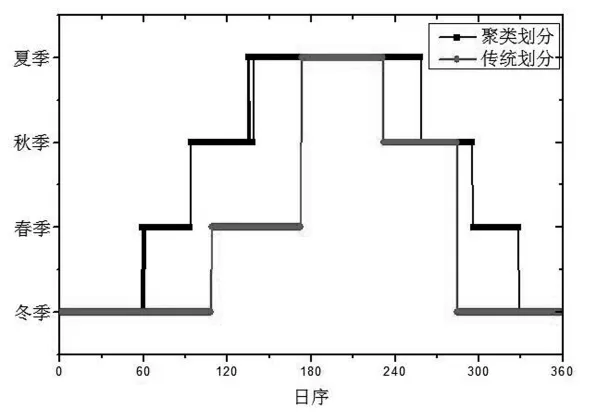
图1 沈阳地区气温的聚类划分与传统划分的对比图

3 预报方程建立

3.1 预报因子选取

选取与温度预报相关的因子，因子包括：500hPa位势高度、700hPa相对湿度、850hPa相对湿度、925hPa相对湿度、850hPa U分量、925hPa U分量、850hPa V分量、925hPa V分量、850hPa垂直速度、925hPa垂直速度、总云量、海平面气压、地面气压、2米相对湿度、2米温度、地表温度、850hPa温度、10米纬向风分量、10米经向风和总降水量，共20个预报因子。

3.2 预报方程构建

将样本随机划分成两部分，80%的样本用于方程模型的建立，20%的样本用于模型的检验。共随机抽取10次，寻求建立最优化模型。构建方程时，核函数采用径向基函数（参数包括：参数c和参数g），通过寻求参数c和参数g，建立最优化模型，参数的选择没有规律，因此需要进行大量试验。回归模型的择优标准为绝对差，损失函数叠加上界为2000，回归迭代最大次数10000。

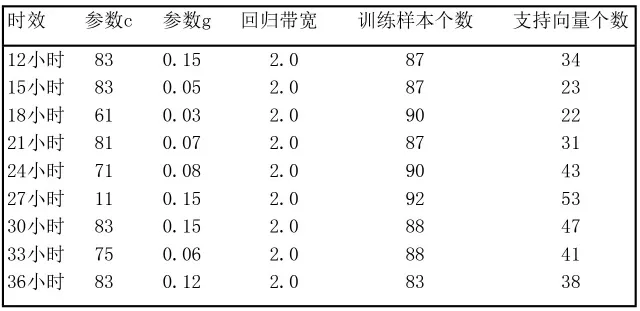
表1 沈阳地区冬季温度客观预报方法参数选取

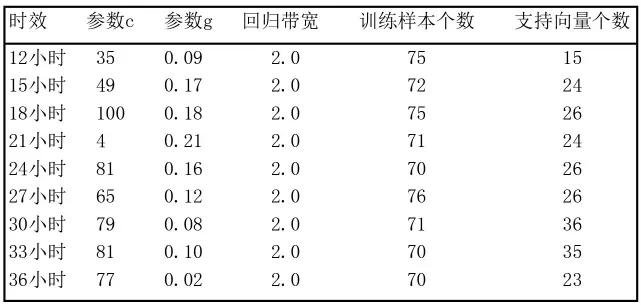
表2 沈阳地区春季温度客观预报方法参数选取

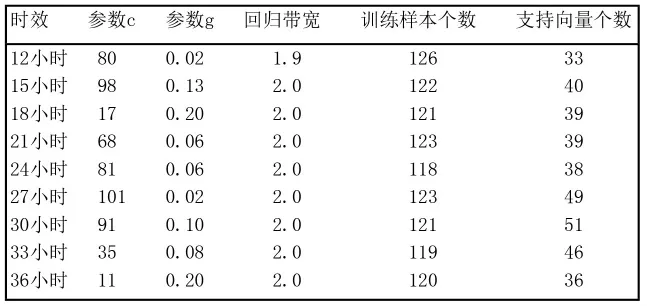
表3 沈阳地区秋季温度客观预报方法参数选取

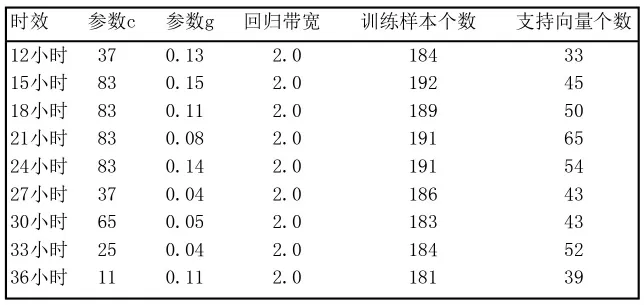
表4 沈阳地区夏季温度客观预报方法参数选取

分析沈阳地区四季温度客观预报方法参数选取表（表1：冬季；表2：春季；表3：秋季；表4：夏季）。冬季参数c：11～83，参数g：0．03～0．15，回归带宽：2．0，支持向量个数占训练样本的24．4%～57．6%；春季参数c：4～100，参数g：0．02～0．21，回归带宽：2．0，支持向量个数占训练样本的20．0%～50．7%；秋季参数c：11～101，参数g：0．02～0．20，回归带宽：1．9～2．0，支持向量个数占训练样本的26．2%～42．1%；夏季参数c：11～83，参数g：0．04～0．15，回归带宽：2．0，支持向量个数占训练样本的17．9%～34．0%。各季节及预报时次的参数之间存在显著差异，由于冬、春季训练样本相对较少，所以依赖的支持向量比重相对多一些。

4 检验

分析沈阳地区冬季温度客观预报方法检验结果（见表5）。温度误差≤2℃的准确率最高为81．1%，最低为52．3%，平均为69．5%；温度误差≤1℃的准确率最高为48．5%，最低为20．3%，平均为33．1%；温度误差≤0．5℃的准确率最高为28．7%，最低为9．2%，平均为18．6%；从结果来看，预报最差的两个时次时效为27小时和30小时，即夜间23时和02时，说明客观方法对夜间降温幅度的把握还存在一定的不足。平均绝对误差除时效27小时外，其他各时次误差都在2℃以内，表明检验样本中，大多数成员的误差都在2℃以内，只有少数成员超过了2℃的误差，客观预报方法是可用的。

表5 沈阳地区冬季温度客观预报方法检验

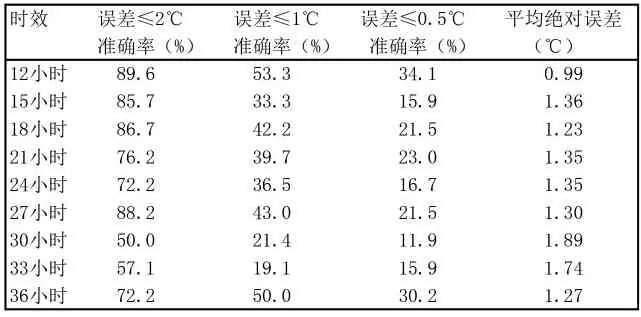
表6 沈阳地区春季温度客观预报方法检验

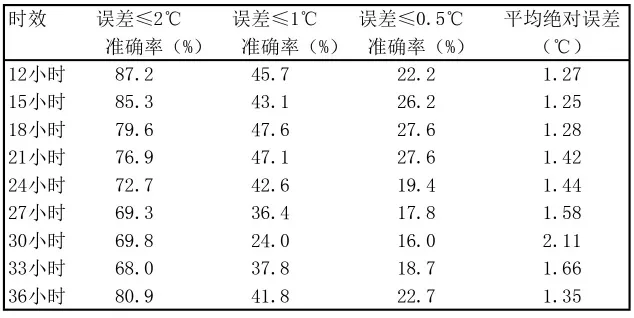
表7 沈阳地区秋季温度客观预报方法检验

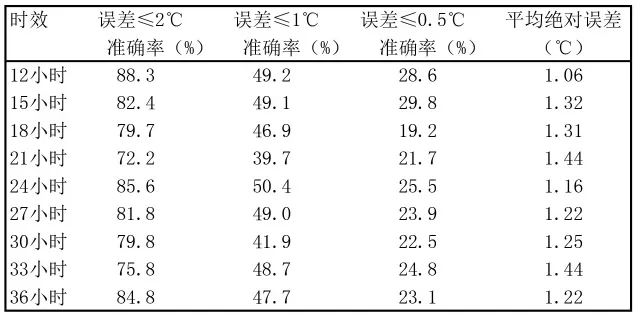
表8 沈阳地区夏季温度客观预报方法检验

分析沈阳地区春季温度客观预报方法检验结果（见表6）。温度误差≤2℃的准确率最高为89．6%，最低为50．0%，平均为75．3%；温度误差≤1℃的准确率最高为53．3%，最低为19．1%，平均为37．6%；温度误差≤0．5℃的准确率最高为34．1%，最低为11．9%，平均为21．2%；春季较冬季预报结果有明显提高，预报最差的两个时次时效为30小时和33小时，即清晨02时和05时，正是夜间最低气温出现的时刻，春季客观方法对夜间最低气温的把握还存在一定的不足。平均绝对误差各时次均在2℃以内，12小时时效误差在1℃以内，表明检验样本中，除少数极端样本预报出现失误外，其他成员均在2℃的误差范围内，客观预报方法可用。

分析沈阳地区秋季温度客观预报方法检验结果（见表7）。温度误差≤2℃的准确率最高为87．2%，最低为69．3%，平均为76．6%；温度误差≤1℃的准确率最高为45．7%，最低为24．0%，平均为40．7%；温度误差≤0．5℃的准确率最高为27．6%，最低为16．0%，平均为22．0%；秋季较冬、春季预报结果有了进一步提高，尤其是夜间最低气温的预报，主要是由于秋季最低气温变化相对平稳。平均绝对误差除时效30小时外，其他各时次误差都在2℃以下，客观预报方法可用。

分析沈阳地区夏季温度客观预报方法检验结果（见表8）。温度误差≤2℃的准确率最高为88．3%，最低为72．2%，平均为81．2%；温度误差≤1℃的准确率最高为50．4%，最低为39．7%，平均为47．0%；温度误差≤0．5℃的准确率最高为29．8%，最低为19．2%，平均为24．3%；夏季客观方法预报是一年四季中最高的，各个时次温度误差≤2℃的准确率都在72%以上，各个时次的平均绝对误差为1．27℃，夏季客观预报方法最为准确。

5 结论

本文采用K-means算法进行季节划分试验，在东北中尺度数值模式WRF-3KM直接输出产品的基础上，基于支持向量机方法，进行交叉验证和预报检验，结果表明：

聚类季节划分与传统季节划分存在差异，将传统的春、秋两季划分为不连续的两类，而传统的夏、冬两季划分的变化不明显，仅在时间长度上存有差异。

支持向量机方法对四季温度进行预报，其中夏季温度预报准确率最高，各时次温度误差≤2℃的准确率平均为81．2%。冬季温度预报准确率最低，各时次温度误差≤2℃的准确率平均为69．2%。冬季客观方法对夜间降温幅度的预报能力存在不足，而春季客观方法对夜间最低气温的预报能力存在不足。平均绝对误差除个别时次超过2℃外，其他时次均在误差范围内，客观预报方法是可用的。

[1]冯汉中,杨淑群,刘波．支持向量机(SVM)方法在气象预报中的个例试验[J]．四川气象,2005(02):9-12．

[2]高永娜,郑华珠,刘沈,等．支持向量机方法在气温预报中的应用[J]．宁夏农林科技,2012,(06):137-139．

[3]王在文,郑祚芳,陈敏,等．支持向量机非线性回归方法的气象要素预报[J]．应用气象学报,2012,(05):562-570．

[4]Vapnik V N．Statistical Learning Theory．John Wiley& Sons,Inc．New York,1998．

[5]Vapnik V N．The Nature of Statistical Learning Theory．Springer Verlag,New York,2000．

[6]Cristianini N and Shawa-Taylor J．An Introduction of Support Vector Machines and Other Kernel_based Learning Methods．Cambridge University Press,2000．

[7]Burges C J．A tutorial on support vector machines for pattern recognition．Data Mining and Know ledge Di scovery, 1998,2：127-167．

[8]Courant R and Hilbert D，Method of Mathematical Physics, Volume I．Springer Verlag,1953．

[9]陈永义,愈小鼎,高学浩,等．处理非线性分类和回归问题的一种新方法（I）——支持向量机方法简介[J]．应用气象学报,2004,15(03):345-354．

[10]冯汉中，陈永义．处理非线性分类和回归问题的一种新方法（Ⅱ）——支持向量机方法在天气预报中的应用[J]．应用气象学报,2004,15(03):355-364．

[11]李凯,常圣领．基于K-means聚类的神经网络分类器集成方法研究[J]．计算机工程与应用,2009,45(22):120-123．

[12]石云平．聚类K-means算法的应用研究[J]．理论与方法,2009,28(08):28-31．

2015年沈阳市科技局项目（F15-109-3-00）和沈阳市精细化预报团队共同资助

S165

A

10.14025/j.cnki.jlny.2017.15.012

鲁杨，本科学历，助理工程师，研究方向：天气预报研究。