基于Arena仿真的事故网络风险耦合特性分析⋆

汪 送

（武警工程大学装备工程学院，西安 710086）

基于Arena仿真的事故网络风险耦合特性分析⋆

汪 送

（武警工程大学装备工程学院，西安 710086）

风险传递过程中，耦合是导致风险突变的重要原因。为提供风险耦合控制方法，给出风险耦合的形式化描述，采用风险耦合弹性系数对耦合强度进行计算；基于Arena软件对某型非致命武器设计论证阶段的进度风险和费用风险之间的耦合特性进行仿真分析，分别仿真了单指标、多指标在线性和非线性耦合情形下的系统行为，结果表明：全局性的线性耦合和高强度非线性耦合能显著改变系统行为。相关结果为风险耦合控制策略的制定提供了参考。

复杂系统，事故网络，风险耦合，弹性系数，Arena仿真

0 引言

随着系统复杂程度的提高，单因素诱发安全事故的情形明显减少，而多因素耦合交互诱发安全事故的案例则日益增多。Leveson教授［1］指出复杂系统事故是“人-机-环”等多种因素耦合交互的结果，Orton等［2］将影响系统安全性的因素称为危险耦元，认为危险耦元通过特定方式相互联系并不断恶化而促成安全事故。由此可见，复杂系统安全事故致因的多因素论已经得到共识。马红岩［3］将事故看作是一个不可逆的、动态演化的开放系统，并建构了事故演化的链式关系结构。事实上，可将复杂系统潜在和显在的各种事故因素及其关联关系所构成的具有递阶层次结构（或立体网状结构）的系统视为复杂事故系统［4］，则复杂事故系统的结构发生突变会诱发安全事故。相对于复杂系统而言，事故系统具有更高的元素聚类性，且元素数目较少，因此，监控其结构稳定性的难度也相对较小。根据结构功能原理，要维系事故系统的稳定，同样需要首先确保其结构的稳定性，使事故系统在面对内外界的干扰和冲击时能快速修复，具体而言就是节点安全裕度不被突破、节点间风险非线性交互（耦合）不发生突变。

刘堂卿等［5］指出当多个风险因素在同一时间、同一地点、同一环境下耦合后，它们之间就会相互影响、相互作用，当耦合后的风险产生共振作用后就会导致风险放大，并将这种风险间的相互影响、相互依赖关系称为风险耦合。在系统风险的形成过程中，各系统部件或子系统间存在功能关联，加上不同风险性质的匹配关系，从而导致各风险事件相互影响、相互作用，最终改变着系统中的风险流量和风险性质，姜宁将其称为安全风险耦合效应［6］。因此，风险耦合主要关注点在于风险间的相互影响和依赖关系。与风险耦合所不同，耦合风险是对某一类特殊风险的界定，如，黎放等［7］认为耦合风险是指体系中的两个（或两个以上的）子体系在通过各种相互作用而彼此影响的过程中，由于事件发生的不确定性而可能引起的影响及偏离预定目标的综合。薛晔等［8］则认为耦合风险指的是复杂的风险系统活动过程中不同风险或风险因子之间的相互依赖和相互影响的关系与程度。

风险耦合更多时候是一种非线性行为（零耦合和弱耦合可以等同于线性交互），对其过程建立合适的数学模型就极富挑战性，更别说对其进行定量分析。因此，本文主要通过仿真手段来分析风险耦合特性，旨在观察不同耦合模式对复杂事故系统动力学特性的影响关系，为进一步研究事故系统的风险演化行为奠定基础。

1 风险耦合的界定与测度

风险演化是指风险的发展变化，特指风险生成（涌现）、传递、耦合、突变到最终诱发事故涌现这一序贯过程。深入揭示风险演化规律，对于科学制定风险控制策略具有较强指导意义。事故网络上风险传递方式主要有链条式风险传递、辐射式风险传递和集中式风险传递3种，具体传递形式如图1所示。根据风险传递过程涉及风险种类的数目，可将其分为单风险传递和多风险传递，在多风险传递过程中就存在耦合效应［9］。在风险演化过程中，风险耦合是导致系统风险发生非线性变化的重要诱因，阐明风险耦合机制是研究风险演化规律的重要前提。

图1 事故网络中风险传递方式

从风险耦合定义可知，要实现对风险耦合的测度，就必须对风险之间的相互依赖程度进行度量，这里引入弹性系数的概念。所谓弹性系数是指在其他条件不变的情况下，风险α变动1%导致与之关联的风险β变动的百分数［10］。

定义2风险耦合弹性系数 定义Sβα为发生风险耦合时，风险α变动1%导致与之关联的风险β变动的百分数，则Sβα为β对α的风险耦合弹性系数，有

风险耦合弹性系数Sβα反映的是事故网络内，一种风险变化对另一种风险变化的影响程度，实际上是对风险间相互影响和相互依赖关系的一种测度。当=0时，表明风险α与风险β之间不存在耦合关系；当为定值时，表明风险α与风险β之间存在线性耦合关系；当为随机变量时，表明风险α与风险β之间存在非线性耦合关系；当时，表明风险α诱发了风险β的耦合突变。

2 案例及其Arena模型

2.1 案例背景

考虑装备研制项目系统，设α为其进度风险，有测度指标［11］：计划论证不够充分α1、技术因素的影响α2、外部条件制约α3、投资强度的影响α4、科技管理的合理性α5；β为其费用风险，有测度指标［11］：预算的不准确性β1、宏观经济调节的影响β2、原材料、配套设备等价格的调整β3、费用管理的不合理性β4。则费用风险β对进度风险α的风险耦合弹性系数为：

进度风险对费用风险的风险耦合弹性系数为：

在考虑风险的耦合时，除了可以考虑不同类型风险之间的耦合弹性系数外，还可以考虑不同风险的测度指标之间的耦合弹性系数，如考虑进度风险α的测度指标技术因素的影响α2对费用风险β的测度指标原材料、配套设备等价格的调整β3的耦合弹性系数，就可以用下式进行计算：

风险耦合弹性系数给出了测度不同风险之间相互影响和依赖关系的手段，在实际运用中可根据不同阶段下风险测度指标的变化值对其进行定量求解，如果求解结果在某一定值附近波动，则可以认为该定值就是两者之间的耦合弹性系数，如果数据波动较大，则可以通过取多个样本，通过数据拟合求得其分布类型，以此来测度风险之间的非线性耦合关系。

2.2 Arena仿真模型构建

考虑某型非致命武器设计论证环节，假设其进度风险和费用风险分别由上述5个和4个指标进行测度，构建其相应Arena仿真模型如图2所示，其中（a）部分为仿真主模型，（b）部分为仿真子模型。模型假定各个风险测度指标均发生有风险熵涌现（可以理解为对预期目标的一种偏离），子模型代表系统资源对各指标涌现出的风险的处置，子模型均有一定节点裕度。初始时刻，1.1～1.5和2.1～2.4都以均值为1随机指数分布涌现，最大值均为40。仿真分析重点考虑风险涌现速率这个自变量，对比分析系统风险熵和后传风险指标，分别考虑单指标（β3对α2）和多指标（β对α）间线性和非线性耦合关系。

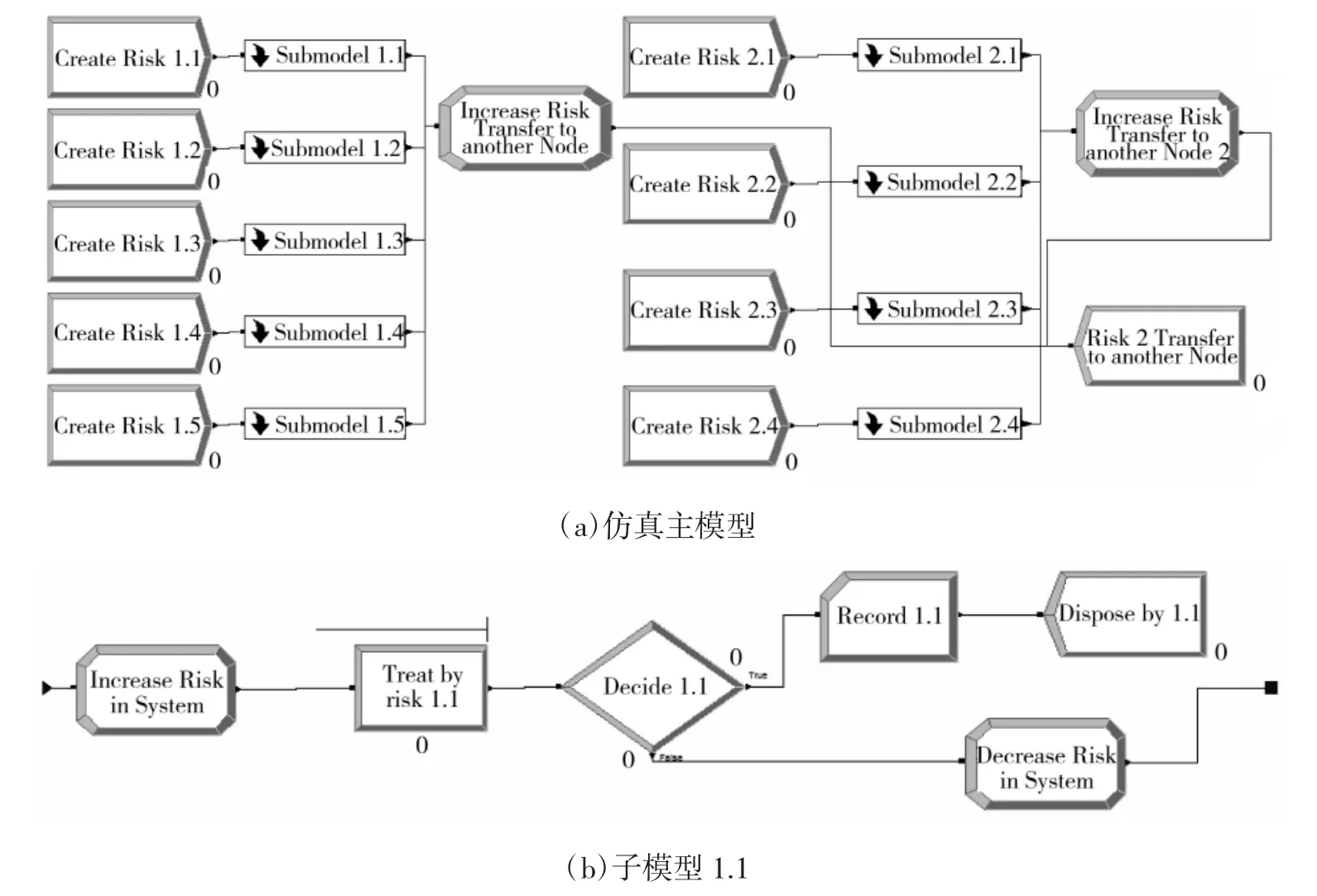
图2 Arena仿真模型

3 仿真结果与分析

3.1 线性耦合仿真结果与分析

从单指标耦合和多指标耦合两个方面进行仿真分析。基于进度风险和费用风险各测度指标的涌现速率，分别设定 Sβ3α2，Sβα的值为 0，1，2，得到如下页图3所示的单指标风险涌现速率线性耦合时系统风险熵的变化图，图4所示的单指标风险涌现速率线性耦合时后传风险熵的变化图，图5所示的多指标风险涌现速率线性耦合时系统风险熵的变化图和图6所示的多指标风险涌现速率线性耦合时后传风险熵的变化图。从图3和图4可知，单指标风险速率线性耦合时，系统风险熵和后传风险熵的波动不大，这说明系统内部的局部线性耦合行为并不会显著影响系统的性能。从图5和图6可知，多指标风险速率线性耦合时，系统风险熵值在不同的风险耦合弹性系数下的最大值波动较大，且最大值的出现时间也有所不同；后传风险熵值虽然波动不大，但是较单指标风险速率线性耦合时的波动幅度还是要大，仿真结果表明，即使是线性耦合，当出现大面积的耦合交互时，系统行为将会受到较大改变。

图3 单指标风险涌现速率线性耦合时系统风险熵的变化

图4 单指标风险涌现速率线性耦合时后传风险熵的变化

图5 多指标风险涌现速率线性耦合时系统风险熵的变化

图6 多指标风险涌现速率线性耦合时后传风险熵的变化

3.2 非线性耦合仿真结果与分析

在线性耦合的基础上，进一步考虑风险测度指标之间的非线性耦合行为。假定指标α2风险涌现服从均值为1，方差为0.2的正态分布，导致指标β3风险涌现服从均值为1的泊松分布，视为单指标耦合。而α 5个测度指标风险涌现服从均值为1，方差为0.2的正态分布，导致β 4个测度指标风险涌现服从均值为1的泊松分布，视为全指标耦合。仿真得到如图7的非线性耦合时系统风险熵的变化图和图8的非线性耦合时后传风险熵的变化图。

图7 非线性耦合时系统风险熵的变化

图8 非线性耦合时后传风险熵的变化

从图可知，非线性耦合时，系统风险熵均较初始时刻值有较大的波动，但后传风险熵波动并不大。出现这样的结果说明正态分布和泊松分布之间虽然是一种非线性耦合关系，但是属于弱耦合，其耦合对系统行为的影响还不及多指标线性耦合时大。因此，针对事故网络中的风险耦合行为，应重点关注全局性的线性耦合和非线性耦合中的强耦合行为，这也是制定风险控制策略的重要依据。

4 结论

（1）界定了风险耦合的概念，采用风险耦合弹性系数对耦合行为进行定量测度；（2）基于Arena软件对单指标、多指标的线性、非线性耦合行为进行仿真分析，结果表明：全局性的线性耦合会显著影响系统的行为，而非线性耦合中的弱耦合虽然在一定程度上能影响到系统的行为，但是作用效果并不明显；（3）杜绝全局性的线性耦合和高强度非线性耦合是复杂系统风险控制的重要举措。

［1］LEVESON N G.A new accident model for engineering safer systems［J］.Safety Science，2004，42（4）：237-270.

［2］ ORTON J D，WEICK K E.Loosely coupled systems：a reconceptualization ［J］.Academy of Management Review，1990，2（8）：203-223.

［3］马红岩.安全事故复杂性演化关系数学表达研究［J］.新乡学院学报（自然科学版），2008，25（2）：7-8.

［4］汪送.基于认知-约束的事故系统风险动力学机制研究［D］.西安：空军工程大学，2013，12.

［5］刘堂卿，罗帆.空中交通安全风险构成及耦合关系分析［J］.武汉理工大学学报（信息与管理工程版），2012，34（1）：93-97.

［6］姜宁.基于风险耦合的交通安全风险因素分析［J］.当代经济，2011，3（上）：124-125

［7］黎放，王悦，狄鹏.武器装备体系作战能力评估中的耦合风险研究 ［J］. 系统工程与电子技术，2008，30（11）：2204-2206.

［8］薛晔，刘耀龙，张涛涛.耦合灾害风险的形成机理研究［J］.自然灾害学报，2013，22（2）：44-50.

［9］孙国强，邱玉霞，李俊梅.网络组织风险传导的动态演化路径研究［J］.中国管理科学，2015，23（2）：170-176.

［10］陈剑辉，徐丽群.弹性系数在供应链风险传导研究中的应用［J］.安徽农业科学，2007，35（1）：313-314.

［11］蒋铁军，王树宗.研制阶段舰船装备总体设计指标体系及其准则［J］.舰船科学技术，2006，28（4）：91-94.

Analysis of Risk Coupling Characteristics of Accident Network Based on Arena Simulation

WANG Song
（School of Equipment Engineering，Engineering University of People's Armed Police，Xi’an 710086，China）

In the risk transfer process，risk coupling is an important cause which leading to risk catastrophe.In order to provide risk coupling control methods，formal description of risk coupling is given，risk coupling elasticity coefficient is used to calculate coupling strength.Based on Arena software to simulate the risk coupling characteristics between schedule risk and cost risk of a type of non-lethal weapons in demonstration phase，the system behavior of single indicators and indicators in linear and nonlinear coupling respectively are simulated，Results show that the global linear coupling and high strength nonlinear coupling could significantly change the system performance.The associated results provide a reference for developing risk coupling control strategy.

complex system，accident network，risk coupling，elasticity coefficient，arena simulation

X913.4

A

10.3969/j.issn.1002-0640.2017.07.011

1002-0640（2017）07-0048-04

2016-05-16

2016-07-22

国家自然科学基金（71401179）；武警工程大学基础研究基金资助项目（WJY201608）

汪 送（1984- ），男，江西衡阳人，博士。研究方向：装备系统工程。