堆放参数对瑞安矿煤堆自燃风速的影响

马 超,吴 宪*,董子文,齐庆杰,周新华,郑 丹

(1. 辽宁工程技术大学安全科学与工程学院，阜新, 123000; 2．矿山热动力灾害与防治教育部重点实验室， 阜新, 123000)

堆放参数对瑞安矿煤堆自燃风速的影响

马 超1,2,吴 宪1,2*,董子文1,2,齐庆杰1,2,周新华1,2,郑 丹1,2

(1. 辽宁工程技术大学安全科学与工程学院，阜新, 123000; 2．矿山热动力灾害与防治教育部重点实验室， 阜新, 123000)

为确定瑞安矿煤堆自燃的环境风速，提高煤堆自燃的预判能力，使用COMSOL Multiphysics 5.0数值仿真软件，开展了5个不同尺寸分别在孔隙率0.2～0.6和环境风速0.05 m/s～13 m/s条件下堆放180 d的自热-自燃过程数值模拟。结果表明，煤堆自燃风速范围因孔隙率和堆放参数不同而异，孔隙率越小煤堆的自燃风速范围越宽，且最小、最易、最大自燃风速与孔隙率之间具有幂函数关系；影响煤堆最小、最易、最大自燃风速显著的参数分别为顶宽、底宽、高度、角度和孔隙率、孔隙率、高度和孔隙率，并构建了三个自燃风速的合理解算方程。

煤堆；自燃；风速；数值模拟；逐步回归

0 引言

煤堆自热可能导致自燃，是一个非常严重的经济和安全问题[1]，同时还会带来严重的环境污染问题[2]。煤堆自燃受风速和孔隙率等影响显著，压实是防治煤堆自燃的首选方法[3]；煤堆堆放条件中任何条件发生细微变化,都可能引起连锁反应，可能引起整个煤堆自燃进程的显著变化，如孔隙率、含水量、粒径等[4]；同时实验研究表明环境条件也是影响煤堆自燃进程较为显著的因素，如风速和环境温度，因此煤堆自燃火灾的灭火工作难度较大，必须提前采取预防措施[5, 6]。这一观点也得到了Alazmi和Vafai[7]、Hooman和Gurgenci[8]的证实，并提出环境风速发生改变使得原有预防措施效果将受到限制；Ejlali[9]采用实验和数值模拟相结合的方法，研究了供风量与煤堆最高温度的关系，指出其他条件不变时，风速对煤堆内最高温度的影响是显著的，风速较大和较小都不会出现高温达到自燃温度的现象，提出煤堆缓慢氧化并产生高温现象需要一定的合适风速范围；Akguna和Essenhigh[10]自行开发了煤堆自燃的二维瞬态数值仿真计算程序，对煤堆的尺寸、存放时间、粒径分布以及孔隙率等进行了模拟研究，上述因素在一定范围内都会显著促进煤堆自燃，都存在一个较易自燃区间或范围；综上所述，煤堆自燃发生和发展趋势及进程的显著影响因素包括煤自身的性质及其堆放尺寸参数及孔隙率、所处环境的风速等[11-13]，因此开展不同堆放尺寸、孔隙率及环境风速条件下煤堆自燃研究对煤堆自燃预防具有重要意义。

本文拟采用COMSOLMultiphysics5.02D多物理场数值模拟软件，建立5种不同堆放尺寸条件下孔隙率0.2～0.6，环境风速0.05 m/～13 m/s时耦合了流场、浓度场、温度场等多场的煤堆自燃瞬态数值模拟二维模型，开展煤堆自燃进程研究，以煤堆自然发火期为指标进行不同条件下的多元非线性逐步回归构建自燃风速综合计算方程，为煤堆自燃预判和防治提供科学规划。

1 建模与计算

1.1 物理模型

如图1，设置研究区域的高60 m,长200 m，风流方向为图1中左向右，右边界为开放出口，煤堆高度H，煤堆底部宽度为Lx，煤堆顶部宽度为Ls，煤堆角度a。

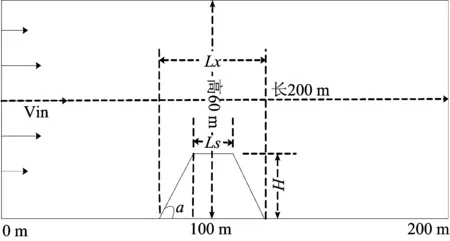
图1 物理模型Fig.1 Physical model

表1 物理模型参数

Table 1 Parameters of physical model

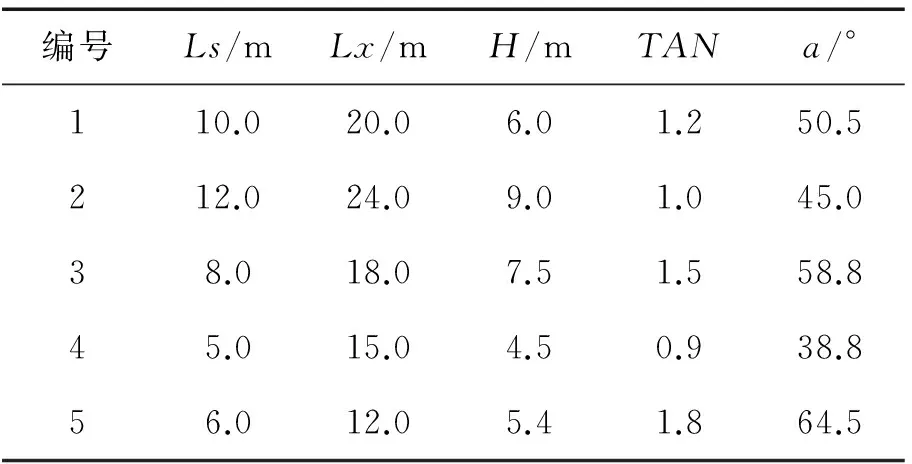
编号Ls/mLx/mH/mTANa/°110.020.06.01.250.5212.024.09.01.045.038.018.07.51.558.845.015.04.50.938.856.012.05.41.864.5

1.2 边界和初始条件

1.2.1 边界条件

(1)自由和多孔介质流动

孔隙率n=0.2、0.3、0.4、0.5、0.6，平均粒径dp=20 mm，渗透率(kp/m2·s-1)由平均粒径和孔隙率共同决定，如式(1)：

kp=n3dp2/(150(1-n)2)

(1)

热浮力，依据式(2)计算：

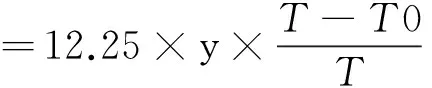
(2)

其中h火为热浮力，N·m-3，y为煤堆高，m。

如图1，左侧为风流入口，右侧出口，入口为风速(Vin)边界条件，出口为风压边界条件。

(2)多孔介质物质传递与扩散

氧气扩散系数(Do2/m2·s-1)依据文献[14]根据式(4)进行计算：

Do2=(0.8011n-0.1616)×

Do20×(T/T0)2/3×p0/p2

(4)

其中Do20为常温下扩散系数，3.5×10-5，m2·s-1；T0为初始温度及环境温度，K；P0为初始气压，Pa；P2为升温后的实际气压，Pa。

煤堆顶部、迎风坡、背风坡3边为空气中氧气浓度边界，9.375 mol·m-3，体积浓度为21%

(3)多孔介质传热

煤的导热系数(λT，J·m-1·K-1)随温度变化如式(6)：

λT=0.00063T+0.1107

(6)

煤堆顶部及两坡面为煤堆与环境的交互界面，采用对流热通量边界控制条件，对流传热系数分别为4.1W/m2/K、1.51W/m2/K。

根据以上边界条件下的设置可以发现3个物理场之间通过流场的风压和风速、温度场的温度、浓度场的氧气浓度进行了有效耦合，将3个独立物理场耦合成一个多场统一的整体，理论上具备了对煤堆自热-自燃问题开展模拟的条件。

1.2.2 初始值

环境的相对湿度为75%，温度为293K(20 ℃)，空气密度1.25kg·m-3，煤堆初始水分3.5%，根据Fierro等[15]的研究水分含量3.5%时水分对自燃的影响可以不予重点考虑；煤中硫化亚铁不是煤自燃的根本原因，但煤中硫含量增加能加速煤的氧化反应速率，加速煤的自燃进程，由于本文研究的煤堆是瑞安公司低硫褐煤，硫含量不足以显著加速煤的自燃，所以同样不考虑煤中硫化亚铁的影响[16-20]；煤的密度1350kg/m3，煤的最短自然发火期为30d～45d，初始气压为101325Pa。

1.3 网格划分与计算

(1)网格划分

为了提高计算精度，网格需要细化，本文采用流体力学标准进行总体网格控制，每个单元尺寸范围为0.1m～0.01m，最大单元生成率1.08，曲折因子0.25，划分后共计15个边界、14个定点、7710个域单元、492个边界单元。

(2)计算

由于孔隙率和风速取值较多，为了节省计算资源采用参数化扫描方法进行组合计算，步长为1d，相对容差1e-6，非线性定常控制阻尼因子0.9，终止方法为每步迭代最大次数5，并采用Anderson加速控制稳定性，模拟煤堆堆放时间为180d。

1.4 模型验证

国电平庄能源股份有限公司瑞安煤矿由于滞销等原因堆积储存大量煤炭，本文以其中一个高约6m，长30m，底部宽度20m，顶部宽10m，平均粒径20mm的梯形煤堆为基础开展数值模拟的准确性验证，煤堆形状如图2；测点布置前分层取样，采用密度法测定煤堆平均孔隙率为0.3。

如图2a，以7.5m为间距取中间3个断面为测试断面，每个断面布置5个测点如图2b，采用AD590温度传感器监测煤堆温度变化，监测周期60d，监测期内平均环境温度27 ℃，平均风速2m/s，取3个断面相同位置测点的平均值绘制曲线如图3a所示，数值模拟建立与该测试煤堆相同的堆放规格及孔隙率模型进行模拟，得到5个测点的温度如图3b所示。

图2 测试断面及测点布置Fig.2 Testing section and measure point

温度监测结果图3a显示，随堆放时间的延长温度总体呈升高趋势，但环境温度、风速、风压等因昼夜和季节性变化以及多次少量的降雨，导致其具有一定的波动性；数值模拟结果如图3b，其结果与现场监测的变化趋势一致，由于上述原因或因素未充分考虑导致数值模拟结果较为平滑，波动性不强。

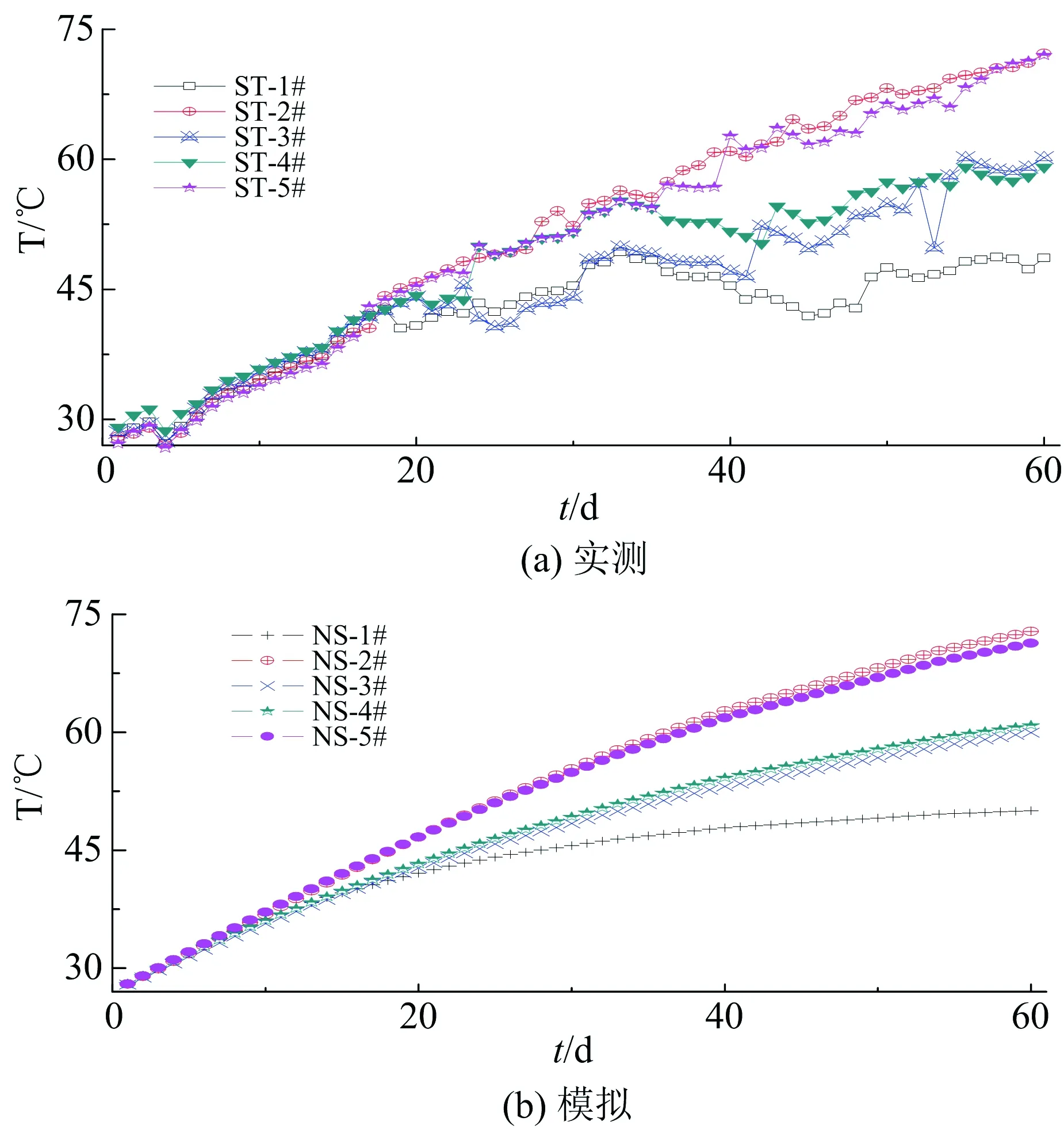
图3 实测与模拟的煤堆温度变化Fig.3 Measured and simulated temperatures

图4 相对误差Fig.4 Relative error

图4为实测与模拟结果的相对误差，5个测点的平均相对误差分别为：3.9%、3.8%、3.9%、0.2%、4.7%；说明相对误差较低，能满足在工程领域中的应用，证明本文所建数值模型是合理的、可靠的。

2 结果分析与讨论

2.1 自燃风速范围及发火期

如图5为1号煤堆孔隙率0.2～0.6时堆放180d条件下煤堆可以引起煤堆自燃的风速及自然发火期。图5中显示，1号煤堆在孔隙率分别为0.2、0.3、0.4、0.5、0.6时自燃风速范围分别为：0.9m/s～9.5m/s、0.4m/s～4m/s、0.25m/s～2m/s、0.15m/s～1m/s、0.1m/s～0.5m/s；最易自燃风速分别为：4m/s、1.8m/s、0.8m/s、0.45m/s、0.25m/s；自然发火期为：43d～175d、44d～131d、49d～156d、48d～106d、48d～85d。孔隙率增加煤堆自燃风速范围逐渐降低，最小、最易、最大自燃风速均降低，最短自然发火期基本不变，最长发火期总体降低，孔隙率相同时煤堆自然发火期因周围风速变化差异较大。

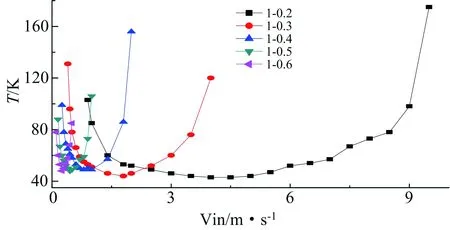
图5 1号煤堆自燃风速及自然发火期Fig.5 Wind-velocity range and time of spontaneous combustion (Coal stockpile No. 1)

煤堆一定时，风速较大条件下孔隙率越小越易自燃，如图5中所示，降低煤堆的孔隙率煤堆的自燃风速向右移动，因此对于孔隙率较大煤堆进行压实会具有较好的防治煤堆自燃的作用，如孔隙率为0.2的煤堆自燃风速范围是0.9m/s～0.95m/s，而孔隙率为0.6、0.5的煤堆自燃风速范围分别为0.1m/s～0.5m/s、0.15m/s～1m/s，当煤堆周围风速在原煤堆自燃风速范围内，将孔隙率0.5～0.6煤堆压实到孔隙率0.2时后煤堆一般不会发生自燃；孔隙率0.4的煤堆自燃风速范围为0.25m/s～2m/s，将孔隙率0.4的煤堆压实到0.2，在周围风速小于0.9时可以保证该煤堆不发生自燃，风速大于2m/s时原煤堆不发生自燃一般不需要进行处理，风速在0.9m/s～2m/s范围内是进行压实该煤堆仍旧会发生自燃，还存在加速自燃现象，因此在该风速条件下不宜进行煤堆压实，应当采用其它措施进行煤堆保护。

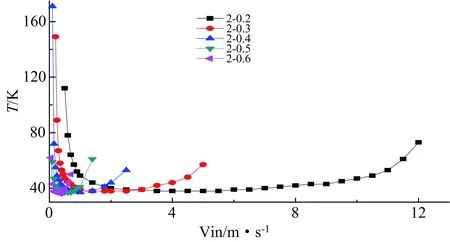
图6 2号煤堆自燃风速及自然发火期Fig.6 Wind-velocity range and time of spontaneous combustion (Coal stockpile No. 2)

2号煤堆在孔隙率0.2～0.6时自燃风速及发火期如图6所示。图6中显示2号煤堆在孔隙率0.2、0.3、0.4、0.5、0.6时的自燃风速范围分别为：0.5m/s～12m/s、0.2m/s～5m/s、0.15m/s～2.5m/s、0.1m/s～1.4m/s、0.05m/s～0.7m/s，最易自燃风速为：3.5m/s、1.4m/s、1m/s、0.4m/s、0.35m/s；发火期分别为：38d～112d、38d～149d、37d～72d、37d～61d、36d～62d。与1号煤堆类似，孔隙率越小自燃风速范围越大，且最小自燃风速、最易自燃风速、最大自燃风速因孔隙率增加而降低，其中最大自燃风速较低最为显著，孔隙率0.2时最大自燃风速为12m/s，孔隙率为0.6时仅为0.7m/s。

如图7为3号煤堆孔隙率0.2～0.6时堆放180d条件下煤堆可以引起煤堆自燃的风速及自然发火期。图7中显示，3号煤堆在孔隙率分别为0.2、0.3、0.4、0.5、0.6时自燃风速范围分别为：0.6m/s～8m/s、0.25m/s～3.5m/s、0.15m/s～1.8m/s、0.1m/s～0.9m/s、0.05m/s～0.5m/s；最易自燃风速分别为：3m/s、1.4m/s、0.9m/s、0.45m/s、0.2m/s。图7中显示，孔隙率一定时，在其自燃风速范围内3号煤堆自然发火期与1、2号煤堆具有类似的变化规律，风速在最小自燃风速条件下时煤堆的自然发火期最长，风速增加自然发火期快速降低到最短，此时对应的风速为最易自燃风速，当风速大于最易自燃风速并逐渐增大到最大自燃风速过程中煤堆自然发火期逐渐延长。

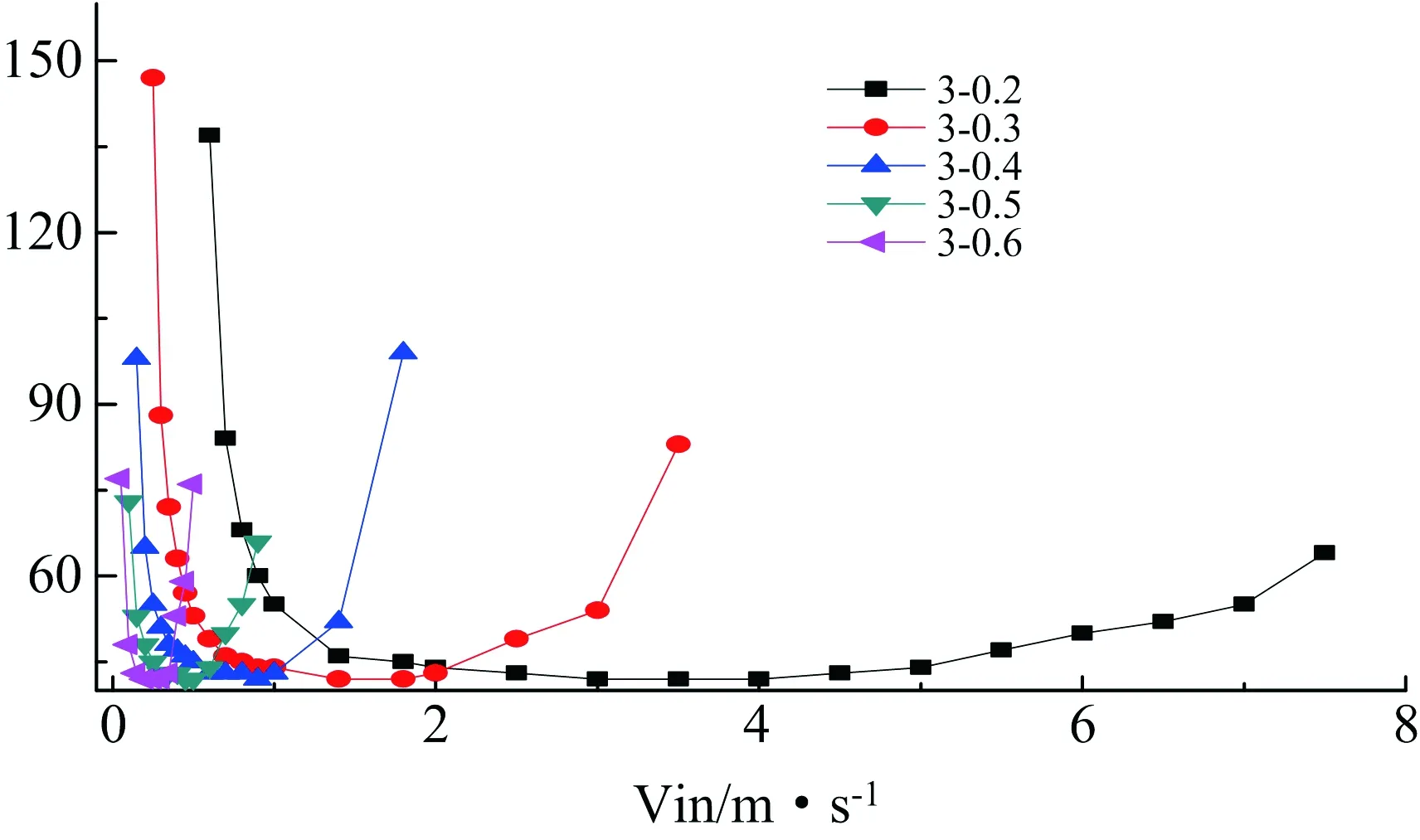
图7 3号煤堆自燃风速及自然发火期Fig.7 Wind-velocity range and time of spontaneous combustion (Coal stockpile No. 3)

对比3号与1号、2号煤堆，在孔隙率相同时不同煤堆之间的自然发火期明显不同，其原因主要在于煤堆的堆放规格参数存在较大差异，因此研究煤堆的自燃风速及等问题时必须充分考虑煤堆堆放的规格参数等因素。研究过程中由于4号煤堆的角度、高度、顶部宽度最小，且底部宽度也相对较小导致其在180d内没有出现自燃现象，因此不对其进行赘述。

与1号、2号、3号煤堆类似，5号煤堆孔隙率不同时自燃风速范围亦不同，孔隙率越小自燃风速范围越宽，且最小、最易、最大自燃风速因孔隙率增加而降低，如图8所示，孔隙率为0.2、0.3、0.4、0.5、0.6时自然发火期分别为：0.6m/s～9m/s、0.25m/s～4m/s、0.1m/s～2m/s、0.05m/s～1m/s、0.05m/s～0.5m/s，最易自燃风速分别为：3.5m/s、1.4m/s、0.7m/s、0.4m/s、0.2m/s；自然发火期分别为：40d～99d、40d～104d、40d～156d、39d～134d、39d～63d。因孔隙率不同煤堆的最短自然发火期差异不大，但最长自然发火期差异较大，且孔隙率增加煤堆最长自然发火期先增后降。

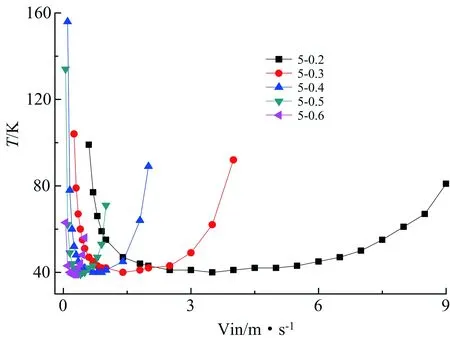
图8 5号煤堆自燃风速及自然发火期Fig.8 Wind-elocity range and time of spontaneous combustion (Coal stockpile No. 5)

综上所述，煤堆能否在一定风速条件下发生自燃，是由其堆放的规格尺寸及孔隙率等不同而决定的，在不考虑煤堆粒径和活性变化的情况下，本文中的4号煤堆由于角度较小，顶底部宽度较小，高度较小等原因综合决定其在堆放180d时不会发生自燃，而1号、2号、3号、5号煤堆均能够发生自燃；煤堆堆放规格尺寸不同在孔隙率相同的条件下煤堆自燃风速范围和发火期不同；同一煤堆孔隙率不同自燃风速范围也存在较大差别；能发生自燃的煤堆，孔隙率越大其自燃风速范围越窄，且引起自燃的最小、最易、最大自燃风速越小。

2.2 最小、最易、最大自燃风速

以上研究了不同堆放规格尺寸煤堆在不同孔隙率条件下的自燃风速范围及自然发火期，煤堆的自燃风速范围是由最小自燃风速和最大自燃风速共同决定的，在自燃风速范围内还有一个特征风速即最易自燃风速，在该风速条件下煤堆的自然发火期最短，以下将对1号、2号、3号、5号4个可自燃煤堆的最小、最易、最大自燃风速进行研究。

图9为1号、2号、3号、5号煤堆的最小(Vmin)、最易(Vy)、最大(Vmax)自燃风速，图9中显示，孔隙率增加，煤堆的最小、最易、最大自燃风速都呈幂函数降低，如式(7)。

Vi=ajn-bj

(7)

式中：Vi为特征风速，包括Vmin、Vy、Vmax

2.3 自燃风速方程构建

由于煤堆堆放参数主要涉及煤堆的角度、高度、顶部宽度、底部宽度等，综合考虑堆放参数和孔隙率时共计需要研究5个变量对煤堆最小、最易、最大自燃风速的影响，一般回归方法很难建立以上方程，因此考虑采用逐步回归法进行方程构建。

假设(xα1,xα2,…xαp;yα)，α=1,2,…,n是变量(x1,x2,…xp;y)的一组观测数据值，观测值“标准化”变换过程中将y视为xm统一处理：

(8)

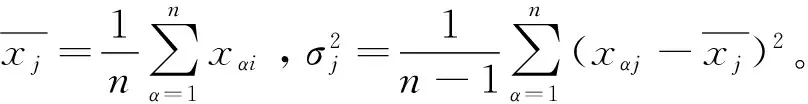
数据标准化完成之后根据最小二乘原理，对标准化的因变量进行三次方处理并以此为变量开展逐步回归，进行综合控制方程的构造，各变量标准化方式如式(9)～式(16)。

Zn=(n-0.4)/0.033287

(9)

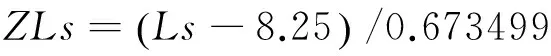
(10)

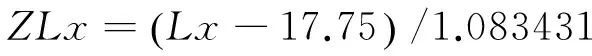
(11)

(12)

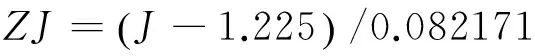
(13)

(14)

(15)

(16)

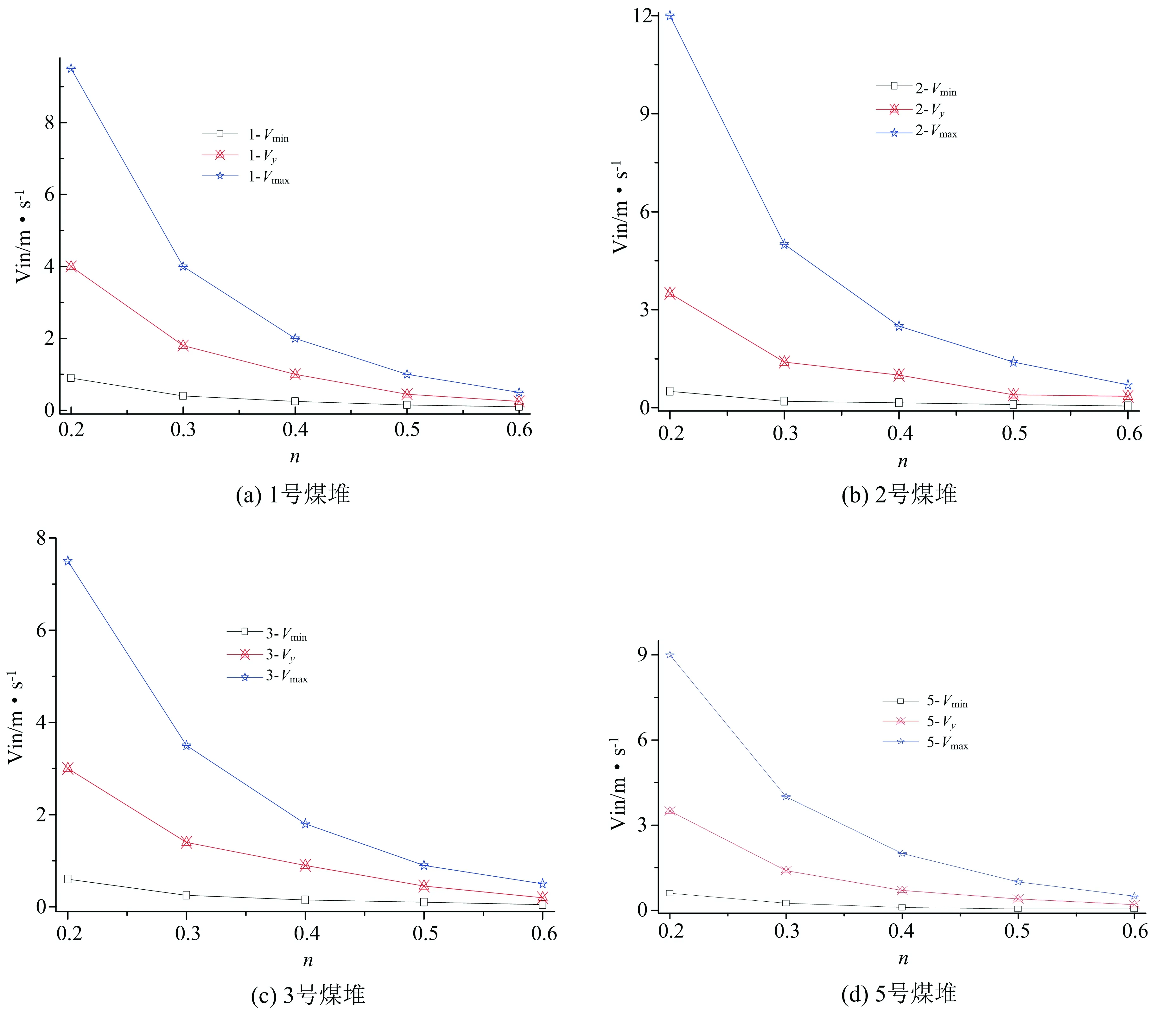
图9 1号、2号、3号、5号煤堆最小、最易、最大自燃风速随孔隙率变化Fig.9 Variation of the Vmin、Vy、Vmax with porosity in 1,2,3,5 coal stockpile

在SPSS中开展逐步回归分析，最小(Vmin)、最易(Vy)、最大(Vmax)自燃风速分别结果7、3、5步回归即可建立回归系数分别为：0.987、0.971、0.991，方程构造合理，建立如式(17)、式(18)、式(19)得计算方程。

ZVmin=1.323-0.014Zn3+0.107Zn2-

0.193ZLsZLx+0.288ZH-0.895Zn+

0.028ZLsZLxZn-0.032ZHZn(R2=0.987)

(17)

ZVy=-1.925-0.53Zn+0.107Zn2-

0.012Zn3(R2=0.971)

(18)

ZVmax=-1.949-0.544Zn+0.108Zn2+

0.159ZH-0.034ZHZn-0.011Zn3(R2=0.991)

(19)

式(17)～式(19)显示，煤堆的孔隙率，顶部宽度、底部宽度以及高度等均对最小自燃风速具有影响，对最易自燃风速影响的关键因素为煤堆的孔隙率，堆放参数对其影响不显著，而最大自燃风速的关键影响因素为煤堆的孔隙率和高度，其它参数影响不重要。由于本文模拟所建立的物理模型为等腰梯形，其顶、底部宽及高度等一定时煤堆的角度也是确定的，因此可以认为影响最小自燃风速的关键因素还包括角度。

为了检验构建的最小、最易、最大自燃风速方程的可靠性，将表1数据代入式(17)～式(19)，结合不同孔隙率，得到表2中的方程求解结果t-Vmin、t-Vy、t-Vmax，表中Vmin、Vy、Vmax为数值模拟结果。表2显示，方程求解结果与数值模拟结果相近，根据表2，最小、最易、最大自燃风速的平均相对误差分别为-2.1%、3.6%、1.8%，说明方程构建合理，对3种特征风速的求解较为准确，能满足工程实践的需要。

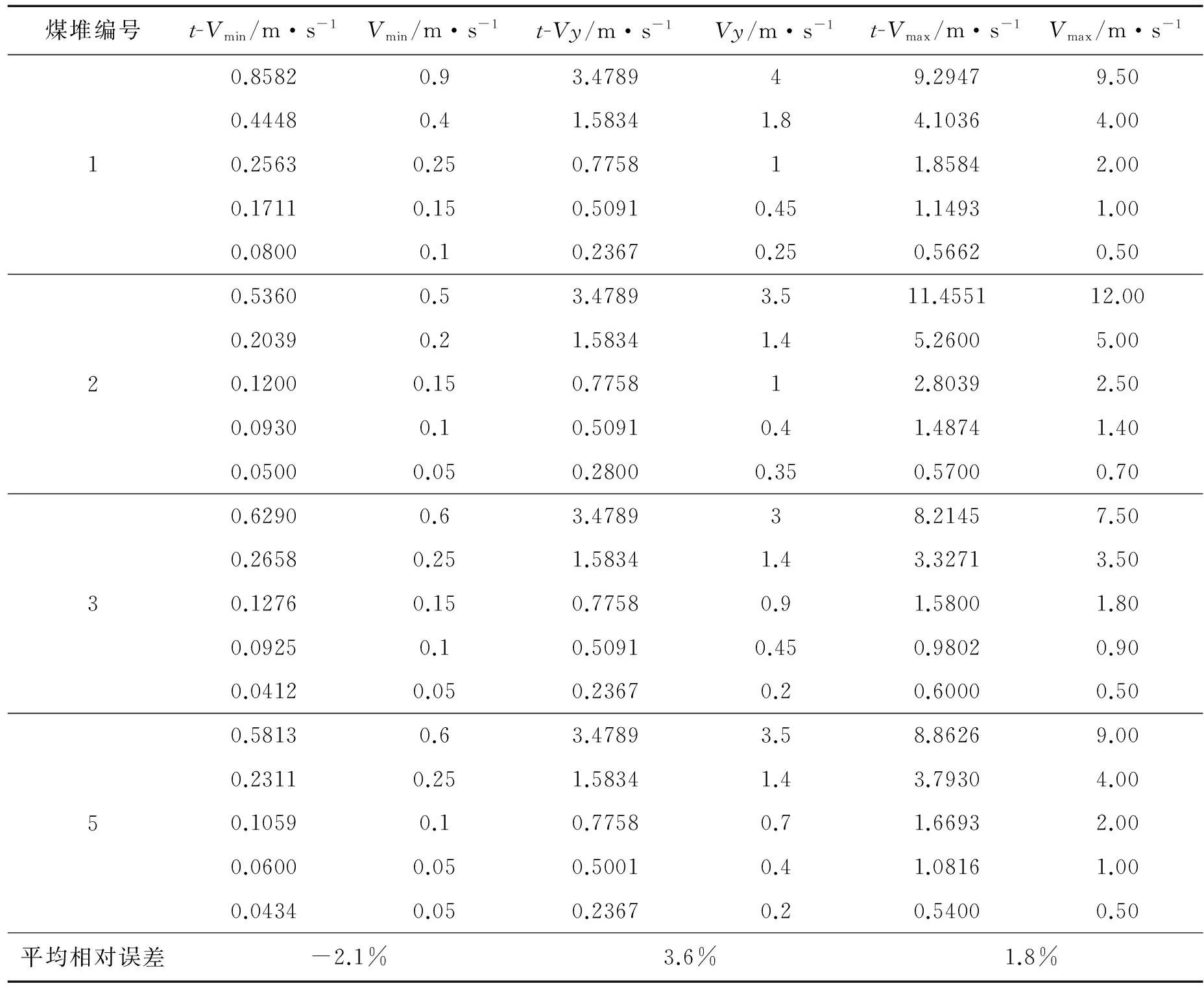
表2 结果对比

3 结论

(1)随风速增加煤堆的自然发火期具有“降低-最短-延长”的规律。

(2)堆放参数一定时，孔隙率越小煤堆的自燃风速范围越宽，且最小、最易、最大自燃风速越大，煤堆的最小、最易、最大自燃风速随孔隙率呈幂函数下降。4个发生自燃的瑞安矿煤堆在孔隙率为0.2、0.3、0.4、0.5、0.6时的最小自燃风速一般为：0.5 m/s～0.9 m/s、0.25 m/s～0.4 m/s、0.1 m/s～0.25 m/s、0.05 m/s～0.1 m/s、0.05 m/s～0.1 m/s范围内，最大自燃风速分别为：8 m/s～12 m/s、3.5 m/s～5 m/s、1.8 m/s～2.5 m/s、1～1.4 m/s、0.5 m/s～0.7 m/s，最易自燃自燃风速分别为：3 m/s～4 m/s、1.4 m/s～1.8 m/s、0.7 m/s～1 m/s、0.4 m/s～0.45 m/s、0.2 m/s～0.35 m/s。

(3)建立了关于孔隙率、顶宽、底宽、高度、角度的能满足工程实践的需要煤堆最小、最易、最大自燃风速计算方程。

[1] Moghtaderi B, et al. Effects of wind flow on self-heating characteristics of coal stockpiles[J]. Institution of Chemical Engineers, 2000, 78(B): 445-453.

[2] Ribeiro J, et al. Petrographic, mineralogical and geochemical characterization of the Serrinha coal waste pile (Douro Coalfield, Portugal) and the potential environmental impacts on soil, sediments and surface waters[J]. International Journal of Coal Geology, 2010, 83(4): 456-466.

[3] 徐精彩. 空气在煤堆中的渗流规律探讨[J].西安矿业学院学报,1995,15(4): 289-293.

[4] 董希琳, 田丽. 湿煤堆自热过程的非稳态数学模拟[J].中国安全科学学报, 1999, 9(3): 38-43.

[5] 张瑞新, 谢和平. 煤堆自然发火的试验研究[J]. 煤炭学报, 2001, 26(2): 168-171.

[6] 张瑞新, 等. 露天煤体自然发火的试验研究[J]. 中国矿业大学学报, 2000, 29(3): 235-238.

[7] Alazmi B, Vafai K. Analysis of variants within the porous media transport models[J] Journal of Heat Transfer, 2000, 122(2): 303-325.

[8] Hooman K, Gurgenci H. Effects of temperature dependent viscosity on forced convection inside a porous medium[J]. Transport in Porous Media, 2008, 75(2): 249-267.

[9] Ejlali A, et al. A new criterion to design reactive coal stockpiles[J]. International Journal of Heat and Mass Transfer, 2009, 36(7): 669-673.

[10] Akgun F, Essenhigh RH. Self-ignition characteristics of coal stockpiles: theoretical prediction from a two-dimensional unsteady-state model[J]. Fuel, 2001, 80(3): 409-415.

[11] Ejlali A, et al. Effects of porosity changes on the self-heating characteristics of coal stockpiles[J]. Journal of Porous Media, 2012, 15(9): 869-876.

[12] 董子文, 等. 风障联合压实防治煤堆自燃技术工艺参数优化[J]. 中国安全生产科学技术, 2016, 12(3): 15-20.

[13] Ejlali A, et al. Numerical modeling of the self-heating process of a wet porous medium[J]. International Journal of Heat and Mass Transfer, 2011, 54(25): 5200-5206.

[14] 杨永良. 煤最短自然发火期测试及煤堆自燃防治技术研究[D]. 徐州: 中国矿业大学, 2009.

[15] Fierro V, et al. Prevention of spontaneous combustion in coal stockpiles experimental results in coal storage yard[J]. Fuel Processing Technology, 1999, 59(1): 23-34.

[16] 吴超, 孟廷让. 水对硫化矿石氧化速度影响的试验研究[J]. 西部探矿工程， 1994, 6(2): 59-62.

[17] 蔡康旭, 等. 高硫煤自燃及其预报方法[J]. 矿业工程研究, 2009, 24(3): 41-44.

[18] Carlson GA, Granoff B. Modeling of coal structure by using computer-aided molecular design[J]. ACS Symposium Series, 1991, 461-465

[19] 张慧君, 等.干燥条件下高硫煤低温氧化特性研究[J].中国安全科学学报, 2012, 22(4): 127-131.

[20] 阳富强, 等. 硫化矿石堆自燃预测预报技术[J]. 中国安全科学学报, 2007, 17(5): 89- 95.

Effects of heap parameters on wind-velocity of spontaneous combustion in Rui An mine coal stockpiles

MA Chao1,2, WU Xian1,2, DONG Ziwen1,2, QI Qingjie1,2, ZHOU Xinhua1,2, ZHEN Dan1,2

(1. College of Safety Science and Engineering, Liaoning Technical University, Fuxin 123000, China; 2. Key Laboratory of Mine Thermodynamic Disaster& Control of Ministry of Education, Fuxin 123000,China)

In order to elucidate the ambient wind-velocity of spontaneous combustion of RUI AN mine coal stockpile, numerical simulations were carried out by COMSOLMultiphysics 5.0 to study the self-heating and spontaneous combustion phenomena, for 5 stack dimensions coal stockpile under the porosity of 0.2～0.6 and wind velocity of 0.05～13 m/s. The numerical simulated time was 180 d. The results show that, the wind velocity of spontaneous combustion varies with the porosity and heap parameters. The smaller the porosity, the wider the wind-velocity range. The smallest, most easily, largest wind-velocities of spontaneous combustion have a power function relation with porosity. Roof and bottom width, height, angle, and porosity are the key parameters which influence the smallest wind-velocity of spontaneous combustion. Porosity significantly influences the most easily wind-velocity of spontaneous combustion. The key parameters which influence the largest wind-velocity of spontaneous combustion are height and porosity of coal stockpile. Integrated computation equations of the wind velocity of coal stockpile spontaneous combustion have been established.

Coal stockpile; Spontaneous combustion; Wind-velocity; Numerical simulation; Stepwise regression

2016-08-15；修改日期：2016-09-12

国家自然基金(51274113)；辽宁省教育厅一般项目(L2015221，L2012122)

马超(1981-)，男，汉族，辽宁凌源人，博士研究生，主要从事矿井火灾防治方向研究。

吴宪，E-mal：1316859454@qq.com

1004-5309(2017)-00114-08

10.3969/j.issn.1004-5309.2017.02.08

X932

A