基于有限元的壁板桩水平承载特性分析
徐金岩,李红文
(浙江广川工程咨询有限公司,浙江 杭州 310020)
基于有限元的壁板桩水平承载特性分析
徐金岩,李红文
(浙江广川工程咨询有限公司,浙江 杭州 310020)
近年来,随着壁板桩的广泛应用,相关研究逐步展开,但水平承载特性的研究成果仅限于现场试验和弹性理论定性分析,且两者所得结果差距比较大。在香港科技大学所做的壁板桩静载试验基础上,使用ABAQUS有限元软件分析壁板桩水平承载特性,并与Zhang的数值模拟计算结果进行比较,试验数据与计算数据非常接近,相差在5%以内,验证了ABAQUS模拟壁板桩水平受荷的可行性。在此基础上分析桩顶位移、桩身弯矩在加载—卸载循环下的变化规律,进一步考虑荷载作用对壁板桩截面的非线性影响,作用力夹角α和位移夹角β相关,当荷载作用方向α = 45°时,荷载与位移方向的夹角最大;x、y方向桩身最大弯矩随荷载作用角度变化而变化,α < 45°,x方向的弯矩能得到有效传递,α > 45°时,y方向的弯矩传递深度加深有限。分析结果有利于对壁板桩水平承载特性的理解,有利于现场试验数据与弹性理论计算结果相结合。
壁板桩;水平承载特性;有限元;三维分析
1 问题的提出
随着工业技术的发展,超高层建筑、大型立交桥、跨海大桥大规模兴建,对基础的要求日益提高,在保证能承受竖向荷载的同时,对水平荷载的承载能力也逐步提高,甚至有时起主导作用。壁板桩作为一种有效的地基处理方法,能够承受较大的竖向荷载,同时也有抵抗较大的水平承载和抗弯曲变形的能力,在地基处理中得到广泛应用。
目前,为了增加基桩水平受荷能力,通常采用增大灌注桩桩径、入土深度以及添加斜桩等措施,却忽略了工程造价。此外,壁板桩横截面力学的非轴对称特性,也增加设计的难度。而对于壁板桩横截面力学非轴对称特性的研究主要采用三维有限单元法,如何评价该特性对水平承载力的影响还存在研究不足[1]。
近年来国内外许多学者用数值分析法对水平荷载作用下桩的受力特性进行了研究。Yang Zhao - hui[2](2002年)建立有限元模型分析水平荷载作用下桩在4种情况(单一黏土,黏土中分布砂土层、单一砂土、砂土中分布黏土层)下的桩身弯矩、剪力、土抗力分布及各深度的p - y曲线;蔡忠祥[3](2014年)采用混凝土塑性损伤模型分析水平受荷桩,分析了竖向荷载、配筋率、桩顶固接对水平承载能力的影响;司海宝[4]基于ABAQUS计算平台,利用二次开发的双屈服面本构模型,开展了遮帘式板桩码头三维数值模拟计算研究。本文在香港科技大学所做壁板桩静载试验的基础上,使用ABAQUS有限元软件分析壁板桩的水平承载特性,并与Zhang[5]的数值模拟计算结果进行比较,利用此模型分析壁板桩水平承载其他特性,为壁板桩的优化利用提供支持。
2 桩体几何模型与材料参数
本文在模拟香港科技大学所做壁板桩静载试验,并与实验数据相比较。验证用ABAQUS分析壁板桩水平承载力的可行性,并拓展研究壁板桩其他方面力学特性的目的。
在试验中,壁板桩(BD1)的截面为l × w = 2.8 m × 0.86 m,长度51 m,在桩顶中心x向(延l = 2.8 m方向)施加1 000 kN荷载,卸载至0 kN,施加2000 kN荷载,卸载至0 kN,施加3 000 kN荷载,卸载至0 kN,施加4 330 kN荷载,并卸载至0 kN,最终水平位移达120 mm。
2.1 有限元网格划分和边界条件
图1为有限元单元划分情况。BD1桩身划分1 632个单元,地基土划分13 200个单元,钢筋划分5 630个单元。整个地基土深60 m、宽30 m、长30 m(根据后面的计算结果可知,水平荷载作用下影响的应力范围都包括在所选的范围之内)。
2.2 模型参数
(1)钢筋混凝土桩。钢筋混凝土桩采用弥散开裂模型,需要的参数有弹性模量E、泊松比μ、混凝土重度γ、极限双轴压缩应力与极限单轴压缩应力的比值rbcσ、失效时单轴拉伸应力与单轴压缩极限应力的比值rtσ、双轴极限压应变与单轴极限压应变的比值rbcε,平面应力状态下,一个方向的主应力达到极限应力,另一个方向裂纹产生时的主拉应力与单轴极限拉应力的比值f。
(2)地基土。地基土采用Mohr - Coulomb模型,需要的参数有弹性模量E,泊松比μ,地基土重度γ、内摩擦角φ。
(3)钢筋。钢筋采用硬化塑性模型,需要的参数有弹性模量E、泊松比μ、钢重度γ,屈服强度fy,极限强度fu。
(4)接触面。接触面采用库伦摩擦模型,需要的参数有摩擦系数u,本文取u = 0.3。
模型计算参数见表1,地基土参数见表2。

表1 模型计算参数表

表2 地基土参数表
3 模拟结果分析
模拟过程基本与试验过程保持一致,加载1 000 kN荷载循环时,桩体处于弹性阶段,不产生塑性变形,可以忽略不计,只模拟施加静荷载2000,3 000,4 000,4 330 kN,并考虑卸载过程,与试验结果比较。
取土体弹性模量E = N、2N、3N作为比较,其中N地基土层的贯入度击数,不同刚度桩周土情况下桩顶水平荷载—位移曲线见图2,其中E = 2N与实测结果比较反分析土体的弹性模量的模拟结果与试验结果最为接近,桩顶荷载— 位移曲线见图3。并且比Zhang的数值结果更接近现场试验,从而验证了ABAQUS模拟壁板桩水平受荷的可行性。

图3 桩顶荷载 — 位移曲线图
3.1 桩顶荷载 — 位移分析
由图3可知,当荷载较小(2000 kN、3 000 kN)时,试验数据与计算数据非常接近,相差在5%以内;在3 000 kN至4 000 kN加载过程中,计算得到:桩顶位移明显增加,超过试验数据。这是因为,在这个过程中,混凝土开裂,钢筋达到屈服极限,桩体基本失去继续承载的能力。
3.2 桩身弯矩分析
壁板桩单桩在分级荷载作用下,并考虑卸载的影响,桩身弯矩在不同荷载作用下随深度变化曲线见图4。由图4可知,在0 ~ 2000 kN加载过程中,弯矩出现第1个峰值,位置大约在泥面下6.0 ~ 7.0 m处;加载至3 000 kN时,弯矩出现第2个峰值,位置在泥面以下8.0 ~ 9.0 m处,可以认为此时桩中的拉应力没有达到极限拉应力,弯矩包络线很饱满;当外荷载达到4 000,4 330 kN,桩体中的拉应力达到极限拉应力时,混凝土开始开裂,钢筋开始受力,弯矩出现第3个峰值,位置在泥面以下8.5 ~ 9.5 m处,可见弯矩的峰值点的位置也是随着荷载的增大而向下移动。
卸载过程与加载过程相对应,当外荷载卸载至0 kN处时,桩身弯矩并没有随之减小为0 kN · m,而是有一定的残余量,且残余量的大小与外荷载对应,卸载前荷载越大,残余弯矩越大。
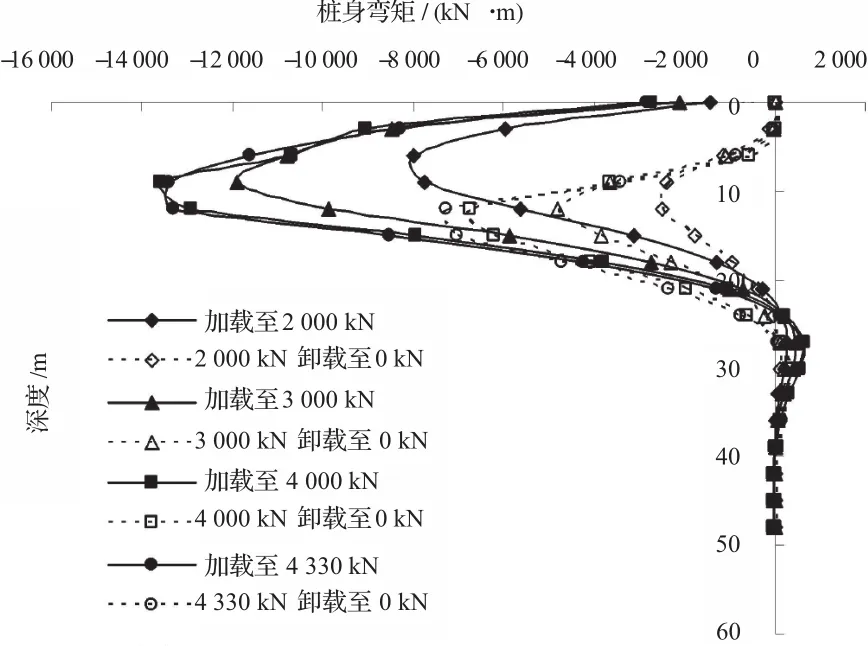
图4 桩身弯矩在不同荷载作用下随深度变化曲线图
4 壁板桩荷载作用方向影响
壁板桩在与x轴夹角为α的荷载作用下的响应,水平荷载F沿角作用在壁板桩桩顶示意见图5,包括桩、土体的应力、位移变化情况。桩顶荷载以集中力的形式施加,利用局部坐标确定其方向,这个力在x、y方向的分力为Fcosα、Fsinα,考虑α = 0.0°、22.5°、45.0°、67.5°、90.0°五个方向,其他条件不改变,在只改变荷载作用角度,比较桩体的应力、位移变化情况。

图5 水平荷载F沿角作用在壁板桩桩顶示意图
F沿(α = 0.0°、22.5°、45.0°、67.5°、90.0°)作用在壁板桩上,α = 0.0°时,桩体的抗弯刚度EIy最大,抵抗水平荷载的能力最强,随着α的增大,桩体的抗弯刚度逐渐减小,α = 90.0°时,抗弯刚度最小,相同荷载作用下壁板桩产生水平位移最大。
图6为峰值荷载沿不同α角作用时,桩身钢筋应力Mises应力云图。随着α角的增加,钢筋最大Mises应力部位也在发生转向,且向地面处移动。这是因为随着α角的增加,桩的抗弯刚度降低,不能够将水平荷载传递到更深的土体,而是在上部产生了塑性铰,桩体抵抗水平荷载的有效深度在减小,承载力必然也随之减小。
图7、8为桩顶荷载沿x、y方向分量—位移分量之间的关系曲线。随着α的角的增大,壁板桩x方向的承载能力下降,即相同的外荷载作用下,桩体的位移增加。同样道理,对于y方向,随着α角的减小,壁板桩y方向的承载能力在下降。由此可见,壁板桩沿x、y轴作用时,对应的x、y方向的承载能力为最大,当荷载偏离x、y轴时,荷载在2个方向的分量会影响彼此方向的刚度。
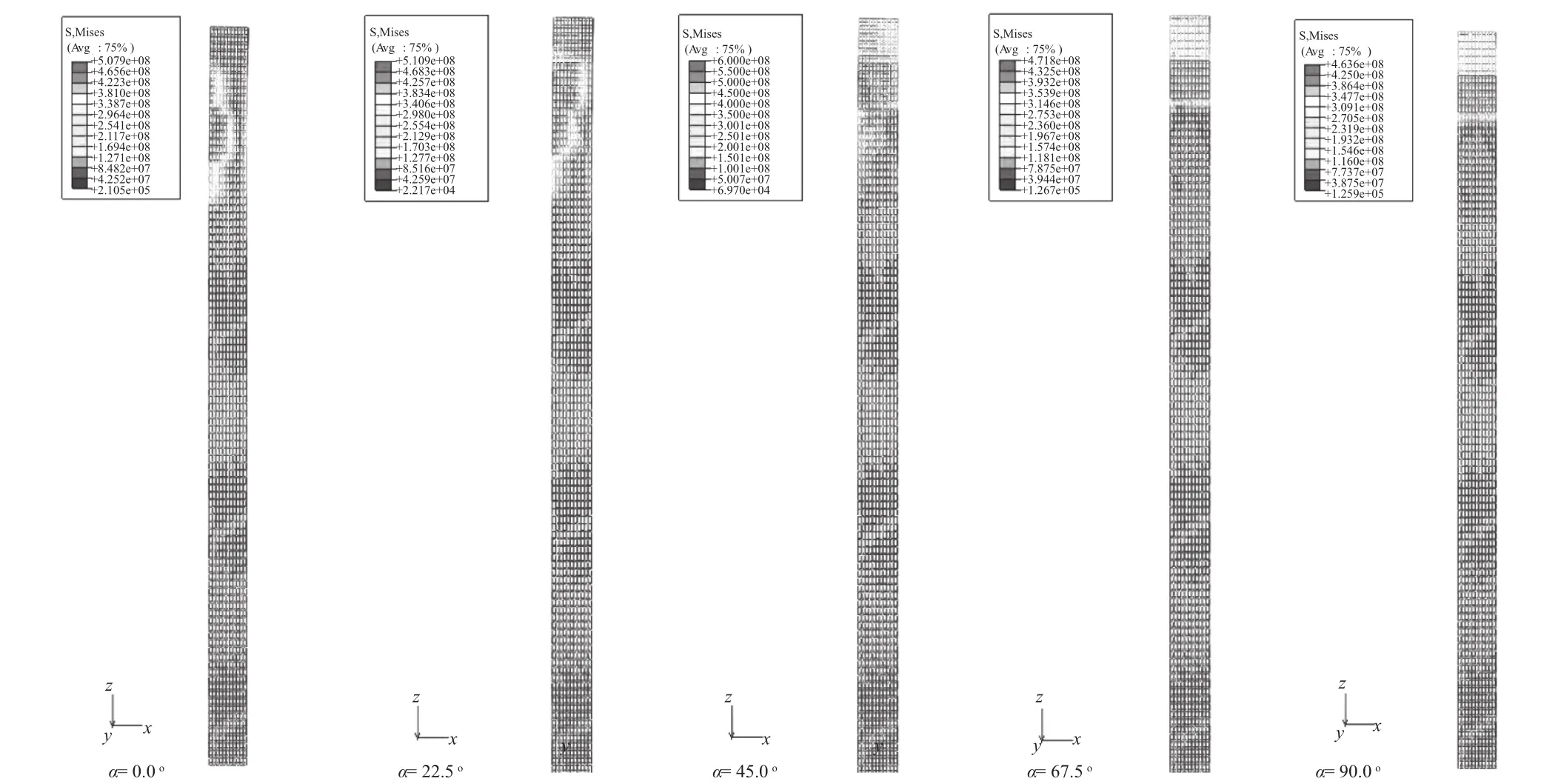
图6 荷载沿不同角度作用时钢筋Mi s e s应力云图

图7 桩顶荷载沿x方向荷载分量 — 位移分量关系曲线图
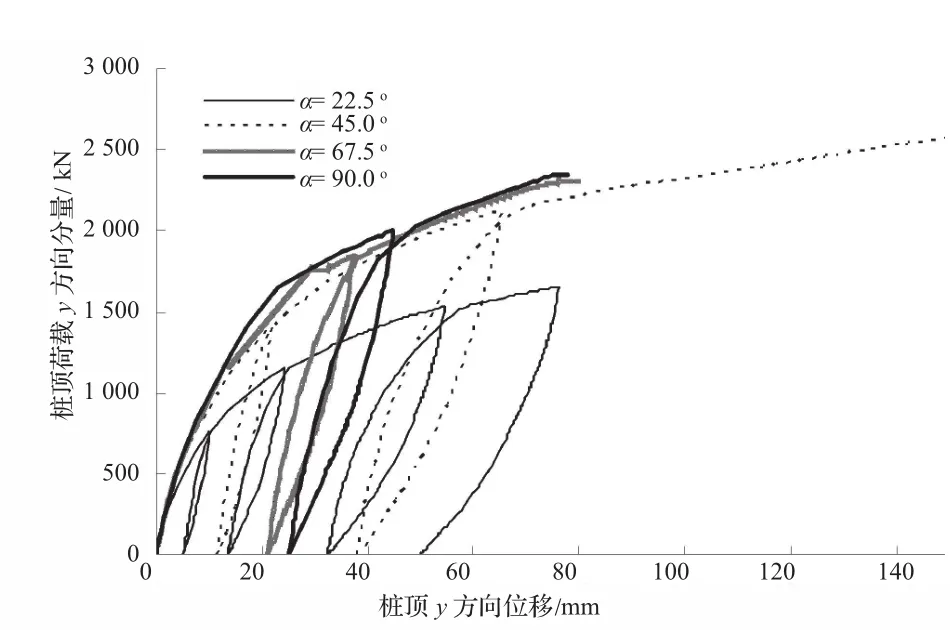
图8 桩顶沿y方向荷载分量 — 位移分量关系曲线图
壁板桩x方向的抗弯刚度EIy是y方向的抗弯刚度EIx的10.6倍,所以,在相同荷载作用下,位移x、y方向分量存在着比较大的差距,因此位移矢量方向与荷载方向存在着一定的偏差,这里用位移与x轴的夹角β来描述位移的方向。图9为β角与α角的关系曲线。由图9可知,α角为22.5°、45.0°、67.5°时,β角随着外荷载的增大而增大,峰值荷载对应的β角,分别是39.0°、72.0°、82.0°。与Zhang的结果接近,再次证明了ABAQUS计算的可靠性。对于圆桩来说,x与y方向的抗弯刚度是相等的,所以α与β相等。
当卸载的时候,β角明显增大,这是因为当卸载时,桩体沿着x方向回弹值明显大于y方向的回弹值,y方向的残余变形与x方向的残余变形的比值持续增加,导致β角增大。并且由4 000 kN卸载至0 kN时β角,要大于对应的3 000 kN与2000 kN卸载至0 kN时的β角,不同的α = 22.5°、45.0°、67.5°卸载后最大β分别为45.0°、71.0°、83.0°,与峰值荷载对应的β 接近。
加载时,对应22.5°、45.0°、67.5°,荷载与位移方向的夹角 | β - α | 的最大值分别为16.5°、27.0°、14.5°。 | β - α |随着α角的增加先增加后减小,α = 45.0°时,夹角最大。

图9 β角与α角的关系曲线图
在不同方向荷载作用下,桩顶荷载与x、y最大弯矩分量关系曲线见图10。由图10可知,x方向最大弯矩明显大于y方向的最大弯矩,随着α的增加,x方向的弯矩最大值明显减小,y方向能够承受的弯矩增长有限,桩体能够承受的总的弯矩在降低,因此也可以得出2个方向的极限弯矩值,x方向的极限弯矩为13 400 kN · m,y方向的极限弯矩为5 000 kN · m。
桩身出现最大弯矩的位置也各不相同,当α < 45.0°,且荷载较小的时候,x方向弯矩最大值出现在泥面以下5.8 m左右,随着荷载的增大,弯矩最大值的位置向下移动,当达到外荷载4 330 kN时,x最大弯矩值出现在泥面以下9.5 m处,y方向的最大弯矩一直在泥面3.1 m附近。
当α > 45.0°时,x方向的弯矩最大值均出现在6.3 m处,而y方向的最大弯矩当荷载较小时出现在3.3 m处,荷载较大时出现在6.0 m处。

图10 桩顶荷载与x、y最大弯矩分量关系曲线
5 结 语
(1)通过对现场试验的精准模拟,当荷载较小时,试验数据与计算数据非常接近,相差在5%以内,比Zhang的数值结果更接近现场试验,验证了有限元模拟壁板桩水平荷载特性的可靠性。
(2)对壁板桩在不同方向荷载作用下的承载力、位移及钢筋应力、桩身弯矩进行详细研究:壁板桩x、y方向的桩身刚度随荷载作用角度变化而彼此影响,作用力夹角α和位移夹角β随荷载变化相关,当荷载作用方向α = 45.0°时,荷载与位移方向的夹角 | β - α | 最大。
(3)x、y方向桩身最大弯矩随荷载作用角度不同而不同,当荷载作用方向α < 45.0°,x方向弯矩最大值位置随荷载的增加而加深,y方向弯矩最大值固定不变;当α >45.0°时,x方向弯矩最大值位置固定不变,而y方向的最大弯矩位置随荷载的增加而加深,但深度加深有限。
[1] 詹金林.水平或竖直受荷壁板桩群桩的变分法分析[D].南京:河海大学,2006.
[2] Yang Z,Jeremić B.Numerical analysis of pile behaviour under lateral loads in layered elastic - plastic soils[J].International Journal for Numerical and Analytical Methods in Geomechanics,2002,26(14):1385 - 1406.
[3] 蔡忠祥,刘陕南,高承勇,等.基于混凝土损伤模型的灌注桩水平承载性状分析[J].岩石力学与工程学报,2014,33(增2):4032 - 4040.
[4] 司海宝,蔡正银,俞缙.遮帘式板桩码头结构与土共同作用3D数值模拟分析[J].土木工程学报,2012(5):182 - 190.
[5] Zhang L M. Behavior of laterally loaded large - section barrettes[J].Journal of geotechnical and geoenvironmental engineering,2003, 129(7): 639 - 648.
(责任编辑 郎忘忧)
Analysis of Lateral Loaded Barrette with the Method of FEM
Xu Jin - yan,Li Hong - wen
(Zhejiang Guangchuan Engineering Consulting Co., Ltd., Hangzhou 310020,Zhejiang,China)
Recently,with barrette foundations widely used,many researchers have been carrying out on the behavior of lateral loaded.However,at present,almost all the researches are limited to field experiment and elastic - theory analysis,the results with the two methods can not coordinate with each other.Using ABAQUS to analyse lateral - loaded barrette based on the static - loaded test of The Hong Kong University of Science and Technology,The simulation results are compared with the value of Zhang to verify the feasibility of the lateral-loaded barrette.Further we consider the nonlinear effect of the load direction on the pile section,When α = 45°,included angle | β - α | of the load and displacement got the maximum result.The maximum bending moment of pile in the direction of x and y varies with the angle of load.When α < 45°,the bending moment of x direction can be effectively transmitted,When α > 45°,the bending moment of Y direction can be Limited transferred to the depth.To investigate the characteristics of lateral loaded barrettes and to set a bridge on the gap of the results mentioned will have a great meaning for the research in the future.
barrette;lateral load;FEM;3D analysis
TV223
A
1008 - 701X(2017)04 - 0055 - 05
10.13641/j.cnki.33 - 1162/tv.2017.04.016
2017-02-10
徐金岩(1983 - ),男,工程师,硕士,主要从事地质工程、水利工程基础工程工作。E - mail:33016803@163.com

