剪式座椅悬架的半主动控制方法
孙明 刘建军 孙勇
(中国汽车技术研究中心)

在现代社会,商用车应用广泛。相比乘用车,其悬架刚度一般较大,振动水平是乘用车振动水平的9~16倍,振动问题更为严重,因此非常容易导致驾驶员过度疲劳,影响驾驶的安全性。目前,可用的方法包括选用合适的轮胎,重型汽车悬架系统和驾驶室采用悬置。除此以外,在座椅结构上采用座椅悬架隔振系统,是提高驾驶员乘坐舒适性的一种有效途径。文献[1]提出了被动座椅悬架模型并对它的振动特性进行了分析。文献[2]通过最优控制算法的直流伺服电机建立了主动式座椅悬架系统。由于使用主动作动器取代悬架系统中的减振器和弹簧,能够很好的隔离车轮和车身传递上来的振动,但本身结构复杂和消耗的能量大,到目前使用范围有限。文献[3]提出了半主动振动隔振系统的概念。文献[4]使用电流变减振器构建了半主动悬架。由于半主动悬架结构简单、低功率输入、力输出范围大及具有较强的鲁棒性,因此最近几十年得到了广泛的应用。商用车使用的剪式座椅悬架由于阻尼原件和弹性原件的特殊安装,传统的单自由度模型不能准确描述悬架特性,因此文章设计了适用于剪式座椅悬架的简化模型及半主动悬架控制策略,以便进一步提高商用车剪式座椅的乘坐舒适性。
1 剪式座椅悬架仿真模型
1.1 剪式座椅悬架ADAMS模型
剪式座椅悬架结构,如图1所示。

图1 剪式座椅悬架结构平面图
根据悬架的真实结构以及各个不同部件之间的实际约束,在ADAMS环境下建立的剪式座椅悬架的仿真模型,如图2所示。

图2 剪式座椅悬架ADAMS模型图
仿真模型中需要的主要部件信息,如表1所示,减振器和弹簧的特性曲线,如3图和图4所示,其中弹簧的预载力为1 400 N。

表1 座椅悬架部件参数
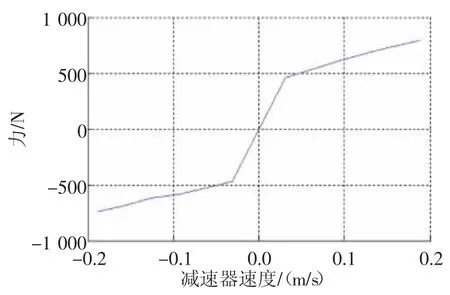
图3 减振器外特性曲线图

图4 空气弹簧的外特性曲线图(0.3 MPa)
考虑到剪式座椅悬架结构和其自身的约束系统比较简单,系统的雅可比矩阵不太容易转变为病态矩阵,因此在ADAMS环境下采用运算速度和准确度较高的GSTIFF积分器中带的IS求解方程,IS求解方程也非常适合求解剪式座椅悬架这种处在低频带运动的方程。其次文章在剪式座椅悬架的ADAMS模型中进行了简化和假设:1)忽略各组件约束连接部位由于相对运动而产生的摩擦力;2)将座垫、靠背及人的质量等效为一定的座椅悬架上底板的质量,而没有将人和座垫以及靠背按照实际的约束单独考虑。
1.2 剪式座椅悬架模型的台架试验验证
为了验证剪式座椅悬架ADAMS中模型的精度,将座椅悬架固定在能做垂向运动的示功机上,并将等效为驾驶员质量的沙袋固定在上底板上,如图5所示,在上底板上安装加速度传感器,通过将台架试验得到的上底板加速度信号和座椅悬架ADAMS模型得到的加速度进行对比,验证模型的精度。在不同激励下的对比结果,如图6所示。

图5 座椅悬架台架试验装置图

图6 正弦激励上底板加速度曲线(振幅20 mm)
由图6对比可知,两者能够很好的吻合,因此说明台架试验可以验证座椅悬架的ADAMS模型具有较高的精度。
2 剪式座椅悬架简化模型
根据对剪式座椅悬架真实的物理结构进行约束分析可知剪式座椅悬架属于单自由度模型,但由于剪式座椅中减振器和弹簧的特殊安装位置(减振器和弹簧并没有安装在上下底板的质心位置)和安装方式(减振器和弹簧都是通过铰接的方式连接在2个固定点之间),在座椅运动过程中,减振器和弹簧与水平面之间的角度都会发生变化,所以减振器阻尼力和上下底板垂向速度的关系和弹簧与下底板垂向相对距离的关系都是非线性的。下面将通过座椅悬架的ADAMS模型得到减振器的垂向外特性(减振器阻尼力和垂向相对速度的关系)及弹簧的垂向外特性(弹簧力和垂向相对距离的关系)。
2.1 弹簧垂向外特性
首先通过在ADAMS环境下,将座椅上底板固定,下底板输入一定的位移信号,使座椅动行程从-0.05 m均匀变化至0.05 m,规定平衡位置处上下底板的垂向相对距离为0。得到弹簧垂向力随座椅悬架上下底板垂向相对位移的变化曲线(弹簧的垂向外特性),如图7所示;弹簧垂向力曲线图,如图8所示。

图7 弹簧的垂向外特性曲线图

图8 弹簧垂向力曲线图
通过拟合可以得到弹簧垂向力与座椅上下底板相对位移的关系,即弹簧的垂向外特性表达式为:

式中:F1v——弹簧的垂向力,N;
sv——座椅上下底板垂向相对位移,m。
2.2 减振器垂向外特性
按照上述方法,首先通过在ADAMS环境下,将座椅上底板固定,下底板输入一定的位移信号,使座椅动行程的速度从-0.05 m/s均匀变化到0.05 m/s。得到的减振器垂向力随座椅上下底板相对速度的变化,如图9所示;减振器垂向力曲线图,如图10所示。

图9 减振器的垂向外特性曲线图

图10 减振器垂向力曲线图
通过拟合可以得到减振器垂向力与座椅上下底板相对速度的关系,即减振器的垂向外特性表达式为:

式中:F2v——减振器的垂向力,N;
vv——座椅上下底板间的垂向速度,m/s,向上为正,向下为负。
2.3 剪式座椅悬架简化模型
根据得到的剪式座椅悬架弹簧的垂向外特性(如式(1))及得到的减振器的垂向外特性(如式(2)),可以得到图11所示的剪式座椅悬架的单自由度简化模型。

图11 剪式座椅悬架简化模型图
剪式座椅悬架垂向振动动力学方程可表示为:

式中:Z——簧上质量位移,m。
将式(1)、式(2)、sv(sv=Z-q)及代入式(3)可得:
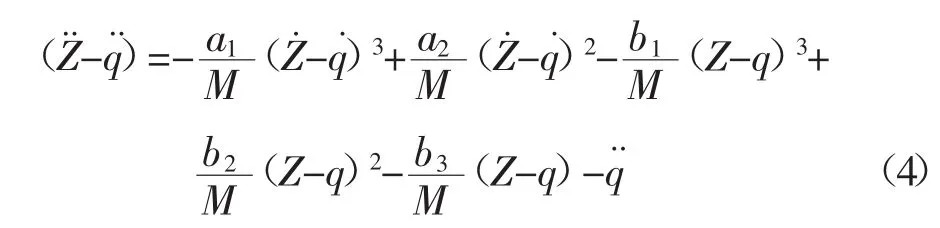
式中:a1,a2,b1,b2,b3——常数,a1=4.3×105,a2=80,b1=2.12×106,b2=0.151×106,b3=1.2×104;
M——车身质量+驾驶员与座椅上底板的等效质量,kg;
q——激励。
令:x1=Z-q,x2=Z˙-q˙为系统的状态变量,则系统的状态方程为:

B1=[0-1]T;
x——定义的系统状态变量;

3 剪式座椅的半主动控制
在对剪式座椅悬架进行半主动控制算法研究之前,首先要推导建立座椅半主动悬架动态方程,将得到的F2v替换为作动器的作用力,得到半主动悬架的模型,如图12所示。

图12 半主动座椅悬架模型图
座椅半主动悬架的运动方程为:
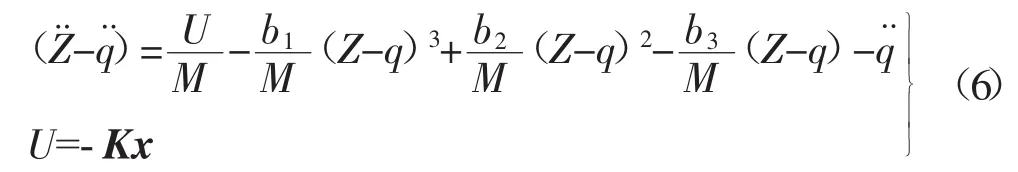
式中:U——作动器的作用力,N;
K——最优控制矩阵,K=LQR(A2,B2,Q,R,N)。

F——外部输入矩阵,F=[0-1]T。
3.1 LQG(线性最优)控制器设计
在设计LQG控制器[5]之前,首先要确定悬架系统的性能指标,针对座椅悬架主要关注座椅乘坐的舒适性,因此在座椅悬架行程允许的情况下,座椅簧上质量的加速度应该尽可能小。因此,LQG控制器设计中的目标性能指标(J)即为悬架动行程和簧上质量加速度的加权平方和的积分值,表示如下:

式中:T——时间,s;
q1——座椅悬架动行程的加权系数;
q2——座椅簧上质量加速度的加权系数。
将式(8)表达为控制理论中熟悉的矩阵形式,如式(9)所示。

由于状态方程是线性时变的,因此每一个仿真步长都要计算最优反馈增益,难于实现实时控制。为克服LQG控制器的缺点,文章将在最优控制器基础上设计模糊控制器来产生最优控制增益,快速地实现座椅悬架的半主动控制。
3.2 模糊控制器设计
最优控制增益(K)的矩阵Q,R,N只与系统状态座椅的动行程(x1)有关,所以认为K也与x1有关,即K是x1的函数K(x1)。因此把座椅悬架上下底板垂向相对位移作为模糊控制器的输入,K作为模糊控制器的输出。通过式(9),离线计算出最优反馈增益系数(K1和K2),得到的K1和K2随x1变化的数据,如表2所示。
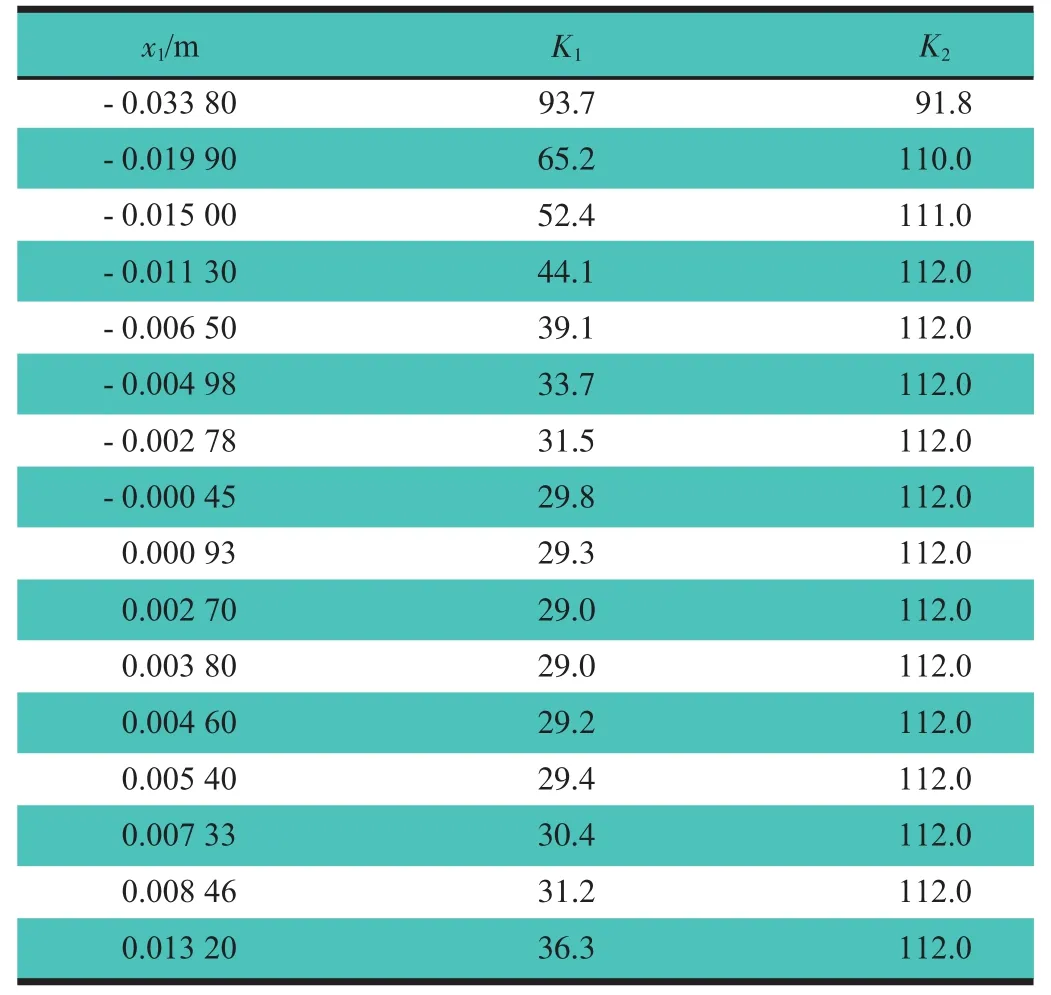
表2 最优反馈增益(K1,K2)随座椅动行程(x1)的变化
根据K1随x1的变化关系将x1分为5段,分别为:

把K1划分为4段,分别为:

可以得到K1的模糊控制规则表,如表3所示。

表3 最优反馈增益(K1)随座椅动行程(x1)的模糊控制规则表
根据K2随x1变化关系x1划分为4段:

把K2划分为2段,分别为:

得到K2的模糊控制规则表,如表4所示。

表4 最优反馈增益(K2)随座椅动行程(x1)的模糊控制规则表
利用MATLAB工具箱进行仿真,得到当座椅下底板的激励为扫频信号,扫频的振幅为0.01 m,频率为0~5 Hz,模糊控制的控制效果,如图14所示。

图13 座椅簧上质量加速度随时间的变化曲线图
由图13可知,扫频激励下应用模糊控制的半主动座椅悬架的簧上质量加速度明显要小于被动座椅悬架簧上质量的加速度,文章设计的半主动座椅悬架能降低座椅簧上质量的振动,提高商用车的乘坐舒适性。
4 结论
文章建立的剪式座椅悬架ADAMS模型具有较高的精度,能够反映真实座椅的振动状态。根据座椅半主动悬架与被动悬架簧上质量加速度的对比可知,半主动座椅悬架的簧上质量加速度在座椅所受的低频带范围内都要小于原被动座椅悬架的簧上质量加速度,验证了文章提出的控制策略能够有效地改善剪式座椅悬架的乘坐舒适性。对进一步提高剪式座椅的乘坐舒适性有一定的参考价值。

