基于MATLAB的支架装配精度优化算法

郭阅

（中国第一汽车股份有限公司技术中心）

在轿车开发过程中，零部件与整车的连接是非常重要的一环，几乎所有的零部件都是通过螺接、卡接或粘接等方式装配到整车上。这些零部件的装配精度直接影响了整车的品质。外观件装配精度差主要影响整车的美观性，重要部件（如底盘件）装配精度差会直接影响整车的性能。在工作中经常遇到由于尺寸链过长而导致零部件装配精度很差或零部件装配不上的情况。为了保证零部件的装配精度，最好将零部件直接连接到整车上，但有时需要在该件与整车之间增加1个支架，增加的支架会导致尺寸链变长，影响最终的装配精度。支架的装配精度会直接影响待装零部件的装配精度。文章对支架不同定位方式对装配精度产生的影响展开说明，提出了一种快速分析及优化零件装配精度的方法。

1 支架的定位

为了减少在生产线上的调整和保证装配精度，支架在装配前需要进行定位，常见的定位方式有：圆孔和长圆孔定位，以及圆孔和圆孔定位等。

1.1 圆孔和长圆孔定位

一般零件设计中常用圆孔和长圆孔进行定位，如图1和图2所示。通常要求长圆孔的长轴与2个螺栓中心点连线同轴，如图1a所示。在这种情况下，即使2个螺栓的实际距离与理论距离存在偏差，粉色件也会有很高的定位精度，如图1b所示。若长圆孔长轴线与螺栓中心连线不平行时，粉件在装配过程中会在其理论位置附近产生一定的偏差，根据假设做出存在装配偏差时的数模，如图2所示。实际上，随着长圆孔长轴线与螺栓中心连线的夹角逐渐增大，零件装配后的位置与其理论位置的偏差也会越来越大。在不同夹角且存在装配偏差的条件下，粉件长圆孔几何中心偏离其理论位置的曲线图，如图3所示。

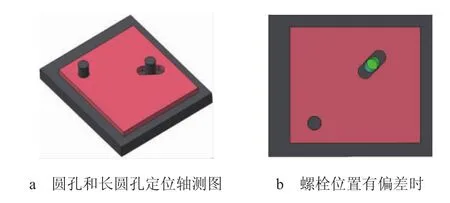
图1 长圆孔长轴与螺栓中心连线同轴示意图

图2 长圆孔长轴与螺栓中心连线不同轴示意图

图3 长圆孔长轴与螺栓中心连线夹角与粉件装配偏差的关系曲线

1.2 小圆孔和大圆孔定位

采用小圆孔和大圆孔定位（如图4所示）的精度不如圆孔和长圆孔定位。如图4a所示，粉色件的主定位孔直径为φ8.2，考虑到M8焊接螺栓与粉件的大孔均存在位置度偏差，假定偏差为±1 mm，则粉色件的大孔至少要开到φ12才能保证正常装配。图4b示出粉件在装配后可能出现的极限情况，其装配位置与理论位置的最大偏差为1.715 mm，定位精度较差。

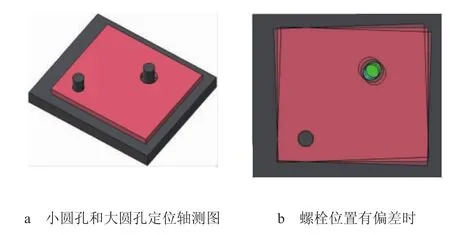
图4 小圆孔和大圆孔定位示意图

1.3 2个等直径圆孔定位

轿车中出现2个等直径圆孔定位的情况很常见，如蓄电池托盘、发动机及变速箱等件均属这种情况。为了满足这些孔的装配精度需要对该件的装配偏差进行分析。

图5示出某电动车的充电机支架，在其上面需要固定充电机等零件，需分析支架固定孔装配偏差以确定充电机能否正常装配。如不考虑螺栓位置度偏差时，充电机支架与螺栓的装配关系可以进行简化，如图6所示，其中里面的2个小圆可视为2个螺栓，其轴心分别为O1，O2；外面的2个大圆可视为支架安装孔，其轴心分别为B，C。显而易见，支架出现最大装配偏差位置时，4个圆一定处于两两相切状态中。将4个圆两两相切的位置都做出来（B，C圆心的位置由4个圆心连线组成的四连杆系统的运动包络可以求出），在其中就可以找到支架最大装配偏差所在位置，即BC与水平轴夹角最大的位置。装配所引起的最大偏差位置即可转化为求解四连杆中的BC杆的最大偏差位置，为方便叙述，将该分析方法命名为四连杆分析法。

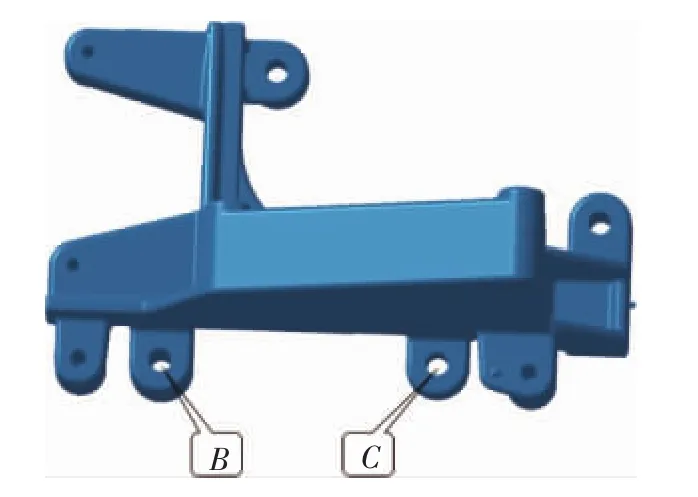
图5 某电动车充电机支架示意图

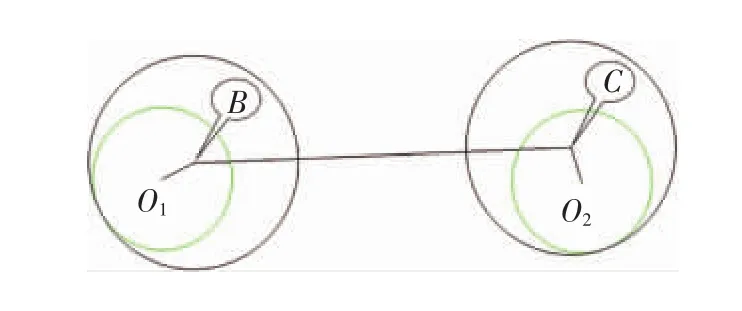
图6 某电动车充电机支架装配关系简化图

2 四连杆分析法

四连杆分析法就是用四连杆机构[1]的运动位置来模拟支架与螺栓装配后的极限位置，从而分析出支架最大装配偏差位置的一种方法。

2.1 四连杆算法及仿真分析

为了不失一般性，建立了充电机支架四连杆机构的通用模型，如图7所示。其中AB杆为原动件（即曲柄），CD杆为从动件（即摇杆），BC杆为连杆，AD杆为机架。将平面四连杆机构看成一个封闭的矢量多边形，可得到如下矢量方程：

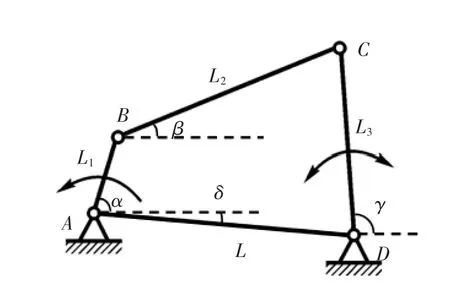
图7 四连杆机构通用模型

因各杆长度不变，当α和γ的值确定后，BC杆的位置（相当于图5中B，C孔心连线的位置）将被确定下来。

各矢量分别向水平轴和竖直轴投影，可列出方程组：

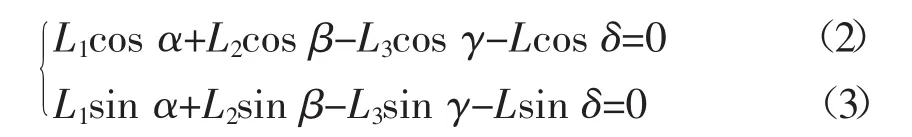
式中：α，β，γ，δ——AB杆、BC杆、CD杆、AD杆与水平轴的夹角，（°）。

因δ是常量，在方程组中消去β便可简化为一个只包含α和γ的方程：

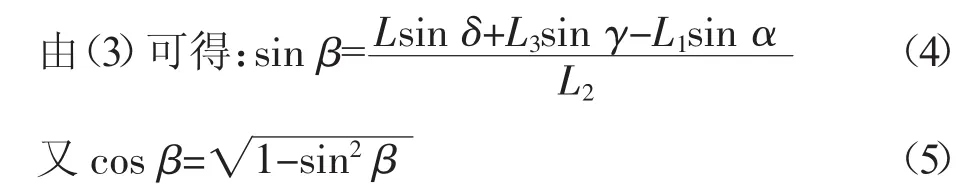
将式（5）代入式（2），可得：

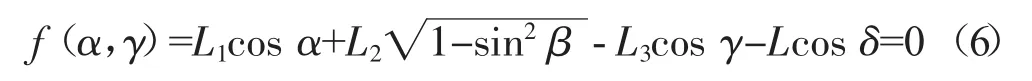
当α给定时，求出能使f(γ)=0的γ值即可。

为了求出γ值，在MATLAB软件中编写一段程序，并做出了四连杆的动态仿真效果。算法简介：因AB杆做圆周运动，α可在（0，2π）内取一组等间距的值，针对每个确定的α值在MATLAB软件中使用fzero[2]函数即可求出对应的γ值。求出所有的γ值后即可做出四连杆机构的动态仿真效果，如图8所示。

图8 四连杆机构动态仿真显示界面

2.2 支架装配偏差分析

图9示出充电机支架的移动坐标系。实际上，文章更关注的是图9中T，S孔装配后的偏差，因为它们是充电机的安装点。为了求解T，S孔装配偏差的极限位置，可以将该支架视为四连杆机构中的BC杆，以B孔心为原点，BC孔心连线为O′X′轴建立直角坐标系。

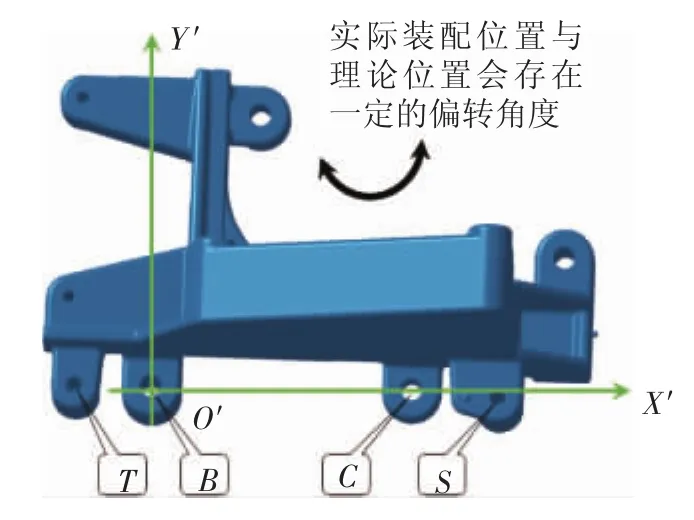
图9 充电机支架的移动坐标系

在模拟支架动态仿真装配时，T，S孔随着支架一起运动，且这2个孔心与O′点的相对位置固定不变。可以通过坐标变换的方法求出T，S孔心的全局坐标，然后就可以方便地找出这2个孔偏差的极值。由分析易知，T，S孔心的最大装配偏差会出现在全局坐标的Y方向上，如图10所示。图11示出充电机支架移动坐标系与全局坐标系的变换关系。

图10 充电机支架所在全局坐标系

图11 充电机支架移动坐标系与全局坐标系的变换关系

在图11所示的二维坐标系中，移动坐标系O′X′Y′中某点的局部坐标（xr，yr）对应全局坐标系OXY中的坐标为（xw，yw），由此可得出2个坐标系之间的变换关系为：

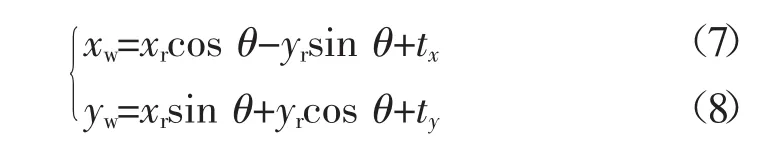
式中：θ——局部坐标系X′轴与全局坐标系X轴的夹角，（°）；

tx，ty——移动坐标系O′点在全局坐标系中的X，Y值，mm。

可以将BC轴心连线作为移动坐标系中的O′X′轴建立局部坐标系，如图9所示，则易求出T，S孔心的局部坐标，由坐标变换公式即可求出支架T，S孔心的全局坐标。

为了计算出T，S点的最大偏差值，文章用四连杆分析法以及坐标变换公式并使用MATLAB软件编写了一个通用化的程序。若某零件有多个安装孔（如上述支架、发动机或变速箱端面的装配孔），只要这个零件使用2个等直径圆孔定位，这个程序就可以快速求出该零件中其余安装孔孔心的最大装配偏差值。这样就可以迅速判断出其余安装孔是否能正常装配，如无法正常装配，可以调整相关的公差值后使用该程序重新计算，最终能够指导用户选择一个合理的公差值。

若想得到更符合实际情况的结果，使用这个程序前需要考虑螺栓以及支架的极限公差（孔径公差及位置度公差等），并在绘图软件（如CATIA）中做出二者两两相切位置的二维图，然后得到考虑极限公差后的四连杆以及T，S点的相关信息。

运行MATLAB程序时只需输入上述参数即可很方便地求出所关心安装点的极限偏差值，图12示出MATLAB优化算法程序运行界面。

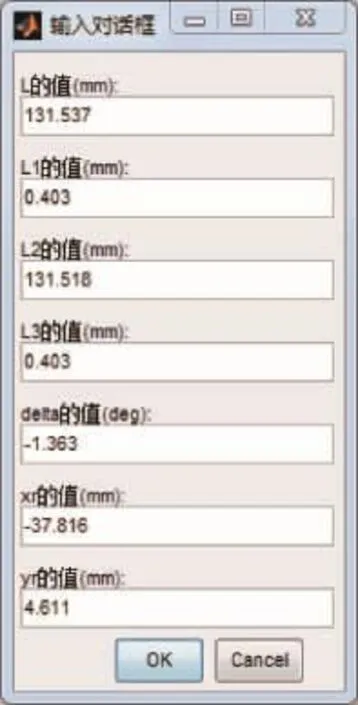
图12 MATLAB优化算法程序运行界面

最终求得S，T点轴心沿全局坐标Y方向与理论轴心的极限偏差分别为-1.15 mm和2.006 mm。

3 程序分析结果的验证

为了验证MATLAB程序计算结果的准确性，在CATIA软件中做出带有极限公差的相关数模并用四连杆分析法进行虚拟样机仿真分析，即DMU[3]分析。

DMU分析后生成了S点和T点的轨迹，如图13所示，在其中可找出极限位置点，如图13中红色“o”形点所示。S点和T点轨迹的断开部分是无解区域，其断点位置与MATLAB程序的分析结果一致。

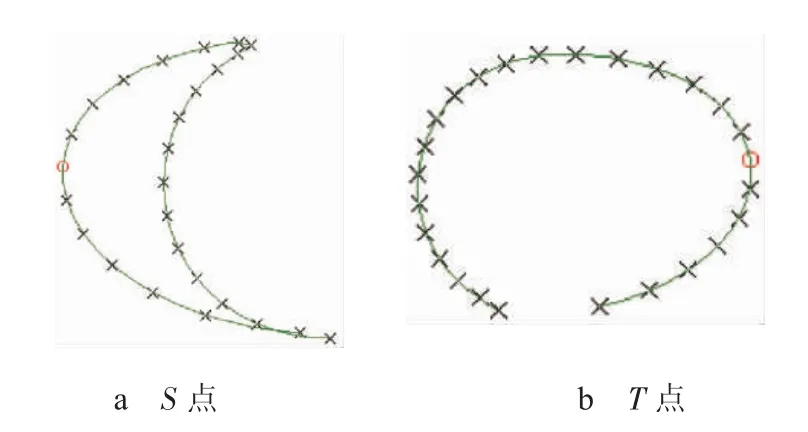
图13 虚拟样机仿真分析中S点和T点的运动轨迹

在CATIA中测出S，T点轴心沿全局坐标Y方向与理论轴心的极限偏差分别为-1.15 mm和2.003 mm，与MATLAB程序的计算结果对比误差非常小，可以认为MATLAB程序的计算结果准确。

4 尺寸公差优化及装车验证

因S，T点轴心偏差已超过充电机固定孔位置度要求（S点处装配孔轴心偏差应＜1 mm，T点处装配孔轴心偏差应＜2 mm），为保证正常装配，将部分公差值进行优化后使用MATLAB程序重新进行了计算。结果为S，T点轴心沿全局坐标Y方向与理论轴心的极限偏差分别为-0.9 mm和1.7 mm，满足充电机的固定要求。

通过实际装车进一步验证了上述优化结果，支架与充电机安装孔匹配良好，验证了相关固定孔尺寸及公差的设置均合理。

5 结论

1）文章对零件不同定位方式的装配精度进行了分析，并提出了一种等直径圆孔定位的装配误差分析方法，即四连杆分析法。

2）使用MATLAB程序计算极大地提高了工作效率。此类问题采用传统手算的方法无法分析，在CATIA中建模与分析的过程大约需8 h，而使用程序计算时先要得到MATLAB程序输入对话框中的相关参数（此过程＜20 min），输入相应值后马上能得出分析结果，为优化设计节省了大量的时间。