基于谱聚类与支持向量机的高校经济困难学生认定方法研究*
莫媛媛,顾明言,张辉宜
(安徽工业大学 现代教育技术与网络管理中心,安徽 马鞍山243002)
基于谱聚类与支持向量机的高校经济困难学生认定方法研究*
莫媛媛,顾明言,张辉宜
(安徽工业大学 现代教育技术与网络管理中心,安徽 马鞍山243002)
为解决当前高校在家庭经济困难学生认定方面缺少直观数据佐证的问题,本文基于在校学生的一卡通消费数据,结合谱聚类算法与支持向量机的优点,探索了一种数据量化的家庭经济困难学生认定方法。首先,对原始数据的每笔消费记录进行标记并采用谱聚类算法对预处理后的学生消费数据进行聚类分析;然后依据聚类结果生成数据筛选规则,剔除离群样本,提取有效的日常消费数据;最后,选取不同的特征构建特征向量并输入到支持向量机(Support Vector Machine,SVM)中训练家庭经济困难学生认定模型。实验结果表明,本文研究的方法能准确地区分出在校生的经济困难程度,在校生的消费信息能较客观地反映出学生的家庭经济情况,该方法将为高校经济困难学生认定工作提供一种有效的辅助手段。
谱聚类算法;特征提取;SVM;经济困难学生认定模型
一、引言
近年来,我国对高校经济困难学生的资助力度逐渐增强,各个高校主要通过经济困难生资助体系给予经济困难学生群体帮助。[1]但资助体系中经济困难学生的认定过程受诸多因素的影响,比如:认定标准难以统一;定性因素、主观因素多,客观依据少,不可避免会出现认定范围和等级的偏差;缺少科学审查和复核办法;对虚报家庭经济状况的行为缺乏有效监督等等。同时经济困难学生的认定涉及教育机会公平、维护高校和社会稳定的重要问题。[2-3]那么如何才能更加公平、公正、客观地评定呢?众所周知,学生在学校使用的校园卡可以直观地体现学生的生活水平,已有部分高校开始对学生校园一卡通的消费行为数据进行研究,并使用数据挖掘技术中的聚类算法和规则分析算法对校园一卡通数据进一步分析。[4-5]王德才等人利用SVM和Apriori关联规则算法分析学生校园一卡通消费行为数据;[6]罗拥军等人采用基于FP-Growth算法寻找学生的贫困度与一卡通数据之间关联关系的依据;[7]黄剑等人利用决策树数据挖掘算法分析学生校园中的消费行为习惯内在关联关系和变化趋势,以便于调整学校餐饮服务;[8]徐剑等人利用K-means算法对一卡通的消费数据进行了聚类分析,并用关联规则算法分析了学生的消费数据与学生成绩之间的关联关系;[9]姜楠等人也利用数据挖掘的K-means算法对学生消费行为进行消费习惯聚类分析,并对聚类结果进行了评估,最后也采用关联规则算法进行学习行为关联度分析。[10]K-means算法在紧凑的超球形分布的数据集合上有很好的性能,然而当数据结构是非凸的,或数据点彼此交叠严重时,K-均值算法往往会失效,而且算法的迭代最优方法不能保证收敛到全局最优解。[11]而另一种聚类算法——谱聚类算法克服了K-means算法的缺点,具有识别非凸分布聚类的能力,适合于求解实际问题,不会陷入局部最优解,且能避免数据的过高维数所造成的奇异性问题。[12-13]谱聚类算法是一种基于两点间相似关系的方法,已被成功应用于语音识别、视频分割、图像分割、VLSI设计、网页划分等领域。[14-16]目前大部分高校对学生一卡通的数据分析多用于研究在校行为分析,对于经济困难学生的认定分析,缺少一些直观、可信度较高的数据作为支撑,多为定性分析,无量化指标。
本文研究了一种基于谱聚类与支持向量机的经济困难学生认定方法,首先对学生行为数据进行规范化处理,采用谱聚类算法对数据进行聚类;通过对聚类结果进行分析,从中选取合适的特征及样本数据;然后采用不同的核函数构建基于支持向量机的经济困难学生认定模型。
二、理论基础
1.谱聚类算法
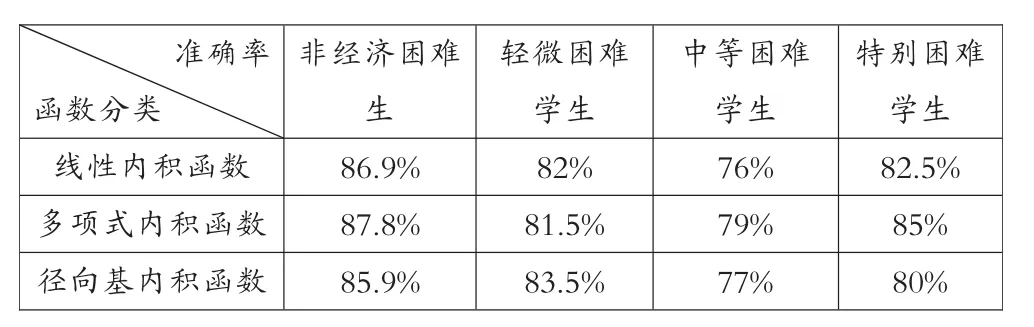
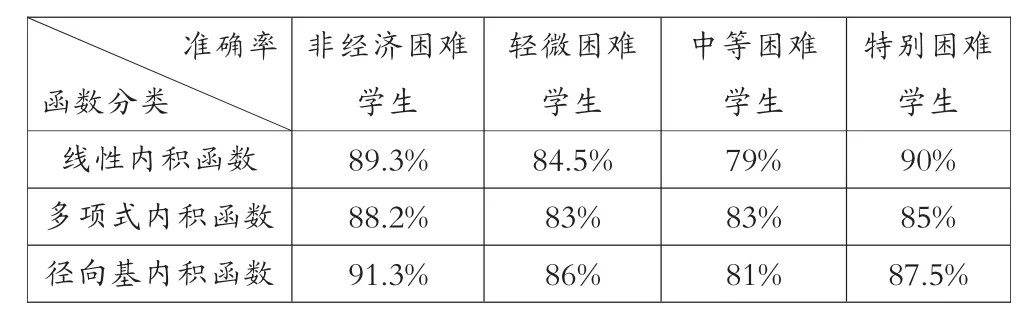
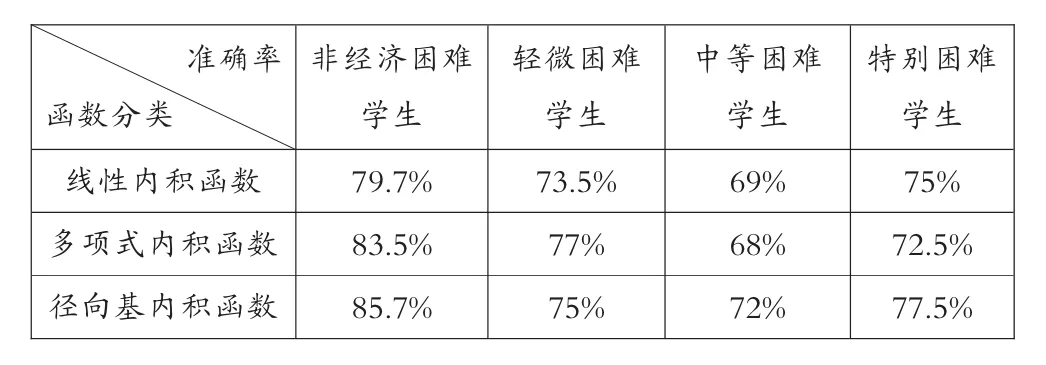
谱聚类是一种点对聚类方法,它能够在任意形状的样本空间上进行聚类,并得到收敛全局的最优划分。[17]谱聚类算法以谱图理论为基础,可简要描述为:对于一个给定的数据集 X={x1,x2, …,xn},x∈RN建立无向带权图 G=(V,E),其中 V={v1,v2,…,vn}是顶点集合,E={eij}是边集合。 每条边 ①构成相似矩阵W。先对数据样本构造无向带权图G=(V,E),将图中每个节点对应的相似数据点连接起来,每条边上的权重代表数据点之间的相似度,相似度一般用高斯核函数来表示,即对于样本数据中两个对象xi和xj的相似度 s: ②计算对角矩阵D。将相似度矩阵W的每一列元素累加起来得到n个数{di}1<=i<=n,以这n个数为对角元素,构成一个n×n的矩阵: ③计算拉普拉斯矩阵L。并利用公式(4)进行归一化处理。 ④计算矩阵的特征值及特征向量,构建特征向量u1,u2,…,un为列的特征矩阵U。从按升序排序好特征值中选择前k个特征值,构建以对应的特征向量u1,u2,…,un为列的矩阵 U∈Rn×n; ⑤设 yi∈Rk(i=1,2,…,n)是对应 U 的第 i行的向量。用 K-means聚类算法,将向量 yi聚类到 C1,C2,…,Ck。 ⑥建立映射,xi∈Rkayi∈Rk(i=1,2,…,n),根据 xi和yi之间的对应关系,利用步骤5中矩阵U的行向量yi的聚类,输出点 x1,x2,…,xn的聚类结果。 2.支持向量机 假设有两类训练样本集, 大小为 l={(xi,yi),i=1,2,…,l},若 xi∈Rn属于第一类,则期望输出为正(yi=+1),若属于第二类,则对应的输出为负(yi=-1),学习的目标是构造一个决策判别函数,针对训练样本集为线性或者非线性的测试数据都能够正确分类。[19] 在样本线性可分的情况下,将N个样本的训练集正确分类的判别函数形式为:y(x)=w·x+b,分类超平面方程为:w·x+b=0。由此训练集能被超平面正确分开,并且要求最近的样本数据与超平面之间的分类间隔最大,即最优分类面,最优分类面上的样本即为支持向量,判别函数为: 式(5)中∂*为最优解,可以通过解下面的凸优化问题得到。在约束条件之下对∂i求以下目标函数的最大值: b*是分类阈值,可以通过两类中任意一对支持向量取中值求得。 对于样本非线性,可以通过非线性函数Φ(xi),同时满足 Mercer 条件的核函数 k(xi,xj)=Φ(xi)·Φ(xj)的条件,将训练数据X映射到某个高维线性特征空间,在高维特征空间中求最优分类超平面,由此得到的目标函数和相应的分类函数为: 支持向量机中最有用的核函数有以下三种: 实验使用的数据存在两个方面的问题:一方面在数据采集、传输的过程中常会造成数据缺失或者数据冗余,而数据的质量直接影响到认定模型训练结果的好坏,所以需要对原始数据进行规范化处理;另一方面,不同学生的消费情况存在一定的差异——不同年级、专业由于课程安排不同(实习、外出交流学习等),往往很多学生一学期内刷卡消费的天数会出现很大的差别;同一个人在不同时期,消费金额也会有较大的悬殊,因此,需要采用有效的方法对学生消费数据进行处理,以得到学生的真实消费数据。 针对这两个问题,分别采用以下解决方法:①去除冗余数据,综合学工、卡机等其他信息来源,对信息缺失的数据进行补全;然后,根据刷卡机所属的部门,梳理出在校生主要的消费去向有餐厅、超市、水果店、书店、精品店、打印、水费、电费、网费、医疗费,关联消费数据及卡机信息,对每笔消费进行标记;最后,对学生消费数据按日汇总,生成日常消费样本数据。②使用谱聚类算法对学生的日消费数据进行聚类,利用聚类结果,对原始数据进行过滤,剔除离群样本,筛选出有效的日常消费数据。文中从三年的一卡通数据中随机选出20万条消费数据,经规范化处理后选取10000条日消费数据用于谱聚类分析。 1.实验数据预处理 购买礼品、就医花费等消费存在偶发性且不具备普遍性,电费为公摊消费无法体现个体用电情况,购书、打印、水费、网费常为一次刷卡,使用较长的时间后才会出现二次消费,不适合作为细粒度的分析。综上,本文对日常消费数据中与生活息息相关的餐饮、超市、水果消费数据进行聚类,以归纳出过高过低等异常消费数据的规则。 文中采用以下几步对样本数据进行聚类:首先,建立消费数据样本集合 X={x1,x2,…,xn},其中,xi=[j1,j2,j3]为第i个日消费数据样本,j1、j2、j3分别为日餐饮、超市、水果消费额。对所有的样本数据,使用公式(1)计算样本数据的相似矩阵W;然后,根据公式(2)计算对角矩阵D,并利用公式(3)计算拉普拉斯矩阵,再利用公式(4)进行归一化处理;而后,计算矩阵L的特征值及特征向量,选取前4个特征向量构建特征矩阵V;最后,使用K-Means算法对特征矩阵进行聚类。根据学生消费情况,将聚类数目设置为4,分别表示异常消费、较低消费、中等消费、较高消费。使用MATLAB工具函数对日消费数据进行聚类,结果如图1所示。 图1 在校生日消费数据聚类结果 从图1可知,消费额处于中间部分的数据占有较大的比例,文中将此部分数据设定为合理的消费并选取较低消费数据、较高消费数据作为有效消费区间 。从原始数据中筛选出满足上述条件的消费数据作为在校生的正常消费数据,然后求取每个学生的日均消费数据。从三年经济困难学生名单中选择有家庭经济状况调查的轻微困难学生600人、中等困难学生 300人、特别困难学生120人及随机挑选出非经济困难学生2040人的日常消费数据,按上述规则过滤并对不同类别 (餐厅、超市、水果店、书店、精品店、打印、水费、电费、网费等)的消费做均值处理,获取共3060条日均消费数据;选用前两年2040条数据作为训练数据输入到SVM训练分类模型,剩余部分作为测试数据。 2.分类模型的训练与结果分析 特征的选取与核函数的选择在训练基于支持向量机的分类模型中具有至关重要的作用,将决定分类模型在实际应用中的好坏,为了比较全面地了解不同的特征、核函数对分类模型效果的影响,实验中做了如下设置:分别选取三组不同类型的消费数据作为特征数据,第一组数据包含餐厅、超市、水果店消费,另外两组数据设置如表1所示;分别采用线性内积函数、多项式内积函数、径向基内积函数,并且选用相同的函数参数来训练模型。 表1 三组不同类型的特征数据设置 实验使用MATLAB中的SVM工具箱进行分类模型的训练和测试。与餐饮消费相比,其他类别的消费额很小,其数值差异较大,文中采用对数函数对三组样本数据进行归一化处理,对数底为2。将分别选用归一化处理后的三组数据通过SVM分类器进行训练,其中每个分类器选用三个不同的核函数,训练完成后共生成三组9个不同的分类器。将与训练数据对应的测试集分别输入三组SVM分类器中进行测试,不同分类模型的认定准确率如表 2、3、4所示。 表2 基于组一数据的经济困难学生认定准确率 表3 基于组二数据的经济困难学生认定准确率 表4 基于组三数据的经济困难学生认定准确率 从上述表1、2、3、4中可以得到以下三个方面的分析结果: ①通过在校生的日常消费数据能较准确地区分出经济困难生与非经济困难生;利用日消费数据鉴别经济困难生困难程度的准确率整体较低,但认定特别困难学生的准确率相对较高;使用三种不同的核函数对经济困难生认定的准确率存在一定的差异,但总体差别较小;使用餐厅、超市、水果店、水费、网费特征数据进行分类的准确率最高,使用所有类别特征数据进行鉴别的正确率最低。 ②使用包含水费、网费消费特征的数据训练出的分类模型的识别准确率较不包含这些特征的分类器的高。由于礼品、就医花费等消费存在偶发性;电费属于公摊消费无法体现个体消费情况,学校图书馆藏较大能基本满足在校生的借阅需求,在校生购书消费率较低,这些不确定因素使礼品、就医、电费等特征干扰了评定模型的准确性,以至于使用所有类别数据进行训练的分类模型的鉴别正确率较低。 ③在校生大都来自于普通家庭,大多未申请经济困难的在校生的消费行为与轻微困难学生的消费情况差之甚微,以至于两者容易分到彼此的类别中,这是造成轻微困难学生认定准确率较低的原因之一;且造成学生家庭特别困难诸如突发性的自然灾害、家庭出现重大变故等客观因素无法从历史消费行为中体现,这是导致难以根据日常消费数据精确区分在校生家庭困难程度的因素之一。 本文使用谱聚类算法对在校生的日常消费数据进行聚类以筛选出真实的消费数据,并构建基于SVM的经济困难生认定模型。实验结果表明,本文采用的方法能较好地区分出在校生是否为经济困难学生,在校生的消费信息能较客观地体现出学生的家庭经济情况,该数据量化的认定方法将为高校经济困难学生评定工作提供一种有效的辅助手段。 [1]陈健,梁思影.高校贫困生认定、资助体系评析[J].高校辅导员学刊,2010(1):24-27. [2]秦微微.基于数据挖掘技术的高校贫困生评判指标的选取[D].东北师范大学,2015. [3]张沂红.基于校园卡系统的学生困难认定辅助评判系统的研究与实现[D].山东大学,2010. [4]王春雁,白雪.高校校园卡系统应用现状及趋势浅析[J].中国教育信息化(高教职教),2011(11):83-87. [5]王雪飞.数据挖掘在高校贫困生校园卡流水数据中的应用研究[D].东北师范大学,2014. [6]王德才.数据挖掘在校园卡消费行为分析中的研究与应用[D].哈尔滨工程大学,2010. [7]罗拥军,罗云芳,陆元路.基于 FP-Growth算法的高校贫困生辅助辨识系统研究与应用[J].广西职业技术学院学报,2016(1):1-4. [8]黄剑.基于决策树数据挖掘算法的大学生消费数据分析[J].电脑与信息技术,2015(5):44-45. [9]徐剑.基于一卡通数据的消费行为与成绩的关联性研究分析[D].南昌大学,2010. [10]姜楠,许维胜.基于校园一卡通数据的学生消费及学习行为分析[J].微型电脑应用,2015(2):35-38. [11]王婷.基于半监督集成的遥感图像的分割和分类[D].西安电子科技大学,2009. [12]杨晓静.基于流形学习的数据聚类与可视化[D].西安电子科技大学,2012. [13]Arbib M A.The handbook of brain theory and neural networks[M].MIT press,2003. [14]Jordan F R B M I.Blind one-microphone speech separation:A spectral learning approach[C].Advances in Neural Information Processing Systems 17:Proceedings of the 2004 Conference.MIT Press,2005,17:65. [15]Odobez J M,Gatica-Perez D,Guillemot M.Video shot clustering using spectral methods[C].3rd Workshop on Content-Based Multimedia Indexing(CBMI).2003(EPFL-CONF-82933). [16]Malik J,Belongie S,Leung T,et al.Contour and texture analysis for image segmentation[J].International journal of computer vision,2001,43(1):7-27. [17]周林,平西建,徐森,张涛.基于谱聚类的聚类集成算法[J].自动化学报,2012(8):1335-1342. [18]彭艳斌,艾解清.基于谱聚类波段选择的高光谱图像分类[J].光电工程,2012(2):63-67. [19]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000(1):32-42. (编辑:王天鹏) G647 A 1673-8454(2017)15-0048-04 中国高等教育学会2016年教育信息化专项课题项目(2016XXZD09)资助,安徽省教育厅智库项目(RD15100228)、安徽工业大学教学改革研究重大委托项目(2016wt03)。



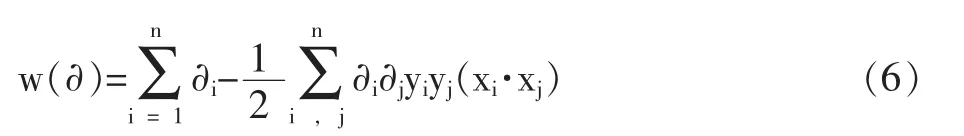


三、实验数据处理及分析


四、结论

