问题引领成为孩子动手操作的风帆

李洁莹

摘 要：随着新课程改革的深入，学生在数学活动中的自主学习和自主探究成为一种重要的学习方式途径。以局部领域的研究学习环节的重要思想为入口，以“三角形内角和”一课为案例，进入小组合作学习，多反馈教学和学生的学习情况，找准在小学数学“空间与图形”的教材中小组合作学习的模式与方向，让学生学会运用已知探索未知的思维方式与方法。

关键词：小学数学；小组合作；探究；空间与图形

自从广州市番禺区“研学后教”课堂教学改革开始，区域内全体教师大致经历了“疑惑期”→“研修期”→“模仿期”→“整合期”。然而，我们要深释“研学后教”的理念，合作交流是学生学习数学的重要方式之一，其意义和价值已经被很多老师所接受。

作为一所农村小学，我们学校的数学研究组试图组织和实施有效的教学研究，以“三角形的内角和”案例研究作为核心，进行实践活动的理论概括，丰富和拓展小学数学“空间与图形”的操作性理论，以“行为反思行为”的方式进行了我们的案例研究，并实践得出了相关的策略。

一、教材的选用与意义

小学数学新教材中“空间与图形”的内容涵盖了每一个学期，有着一定的代表性。考虑到四年级的孩子有一定的生活经验和操作能力，所以选择此内容。通常因为很多孩子都知道三角形的内角是180°，所以教师表面上所教的学生都懂。然而，这180°的本质学生却无法理解。

我们组分析，三角形的内角是这部分知识的空间和图形，动手学习的方法是有效的。在教学过程中，让学生探索这个问题的新知识，运用手中的学具动手操作，通过量、剪、拼、折叠的方法获得结论，获得的不单是一个三角形内角和的知识，而且让学生学会了由已知探索未知的思维方式与方法。在学习活动中借助探索实践，引导数学学习，是本课的亮点。

二、案例回放

“三角形的内角和”教学片段一：

本课中当我提出“为什么一个三角形中不能有两个角是直角”时，有学生指出如果有两个直角，它就拼不成一个三角形；也有学生说“如果有两个直角，它就趋向于长方形或正方形”。为什么会这样呢？学生沉默片刻后，忽然有个学生举手了：“因为三角形的内角和是180°，两个直角已经有180°了，所以不可能有两个角是直角。”这样的回答把本来设计的教学环节打乱了，此时我灵机一动把问题抛给学生：“你们理解他说的话吗？你怎么知道内角和是180°？还有谁知道三角形的内角和是180°”等，当我看到大多数学生已经知道这一知识时，我就把学生直接引向主题“自己研究证明一下三角形的内角和是不是180°。”

“三角形的内角和”教学片段二：

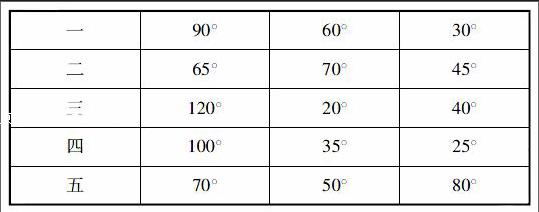
请同学们用下表每组的三个角拼成三角形，看谁拼得快。

学生操作后，发现后面两组怎么也拼不出三角形？

师：为什么前面三组的三个角能拼出三角形，后面两组却拼不出呢？仔细观察，你发现了什么？

学生观察后。

生1：我发现前面三组的三个角加起来都等于180°。

生2：我发现第四组三个角加起来等于160°，不是180°。

生3：我发现第五组三个角加起来是200°。

生4：我想三个角加起来等于180°时就能拼成三角形。

师：三角形的三个角加起来，我们可以说成是三角形的内角和。那你们是说三角形的内角和是——

生：180°。

师：这是两个什么样的平面图形？这两个图形有什么联系？

生1：它们都有四个直角。

生2：它们都有四条边。

生3：它们都能沿对角线分成两个完全一样的直角三角形。

师：同学们观察得真仔细！我们沿着长方形和正方形的对角线对折就会把长方形和正方形平均分成两个完全一样的直角三角形。请同学们利用学具当中的正方形和长方形纸片动手折一折，并思考：这样两个完全一样的直角三角形，它们的内角和各自有多少度？

學生因为需要主动进行合作和交流，或者被老师安排沟通交流，两种心态会产生不同的影响。如何激发学生在合作和交流中的主动性？我有一个更深刻的认识，有两点值得我们注意：

1.让问题更具有思考性和探索性

在案例教学中，四一班的教法是，用一种方法证明三角形的内角和，让他们谈什么？只会不断地重复量一量，因为学生较多使用最直观的方法。但在四二班的教学中，笔者建议先选择研究方法，然后再证明小组成员必须进行沟通与合作。特别是听其他小组时有不同的证明方式，好奇心理促使他们一定想进行沟通和交流，然后讨论才会热烈。

2.以组间竞争促组内合作

竞争与合作不是相互排斥的概念，而是相互促进的。四二班的教学，引入小组之间的竞争机制，这样就会促使小组成员主动参与分工协作，不再由老师安排合作，组织沟通。试想，在四二班的教学中，如果老师说“看谁最快？”他们的合作情况会怎样？因此，在小组学习交流之后，教师必须关注小组的整体观点而不是个体。评判也要以小组为单位。

三、我们的策略

在“空间与图形”的内容中，教师应遵循认知规律，引导学生展开“具体→半具体半抽象→抽象”的概括式学习过程，体验“经验→模型→符号”的数学化过程。

第一步：根据观察到的问题作出猜测，建立模型，然后修改，调整模型，然后一般化，这是现代人的思维方式。

第二步：操作方法

（一）激趣，在教学中，教师要创设问题情境，发挥小组合作的目的，激发学生参与动机，明确合作目标是什么及如何研究，使学生知道为什么学及如何学习。

（二）巧导，教师的指导应与学生讨论相结合。在学生自主学习的基础上，教师要善于引导和组织学生进行讨论，积极参与学生的讨论，收集信息，发现问题，及时指导。

（三）敢问，教师的提问要综合学生问题，让学生在合作学习的过程中进行充分的讨论，发现问题，大胆提出问题。

（四）择时，教师要选择恰当的合作时机。

1.学生的思维受阻，可以组织合作讨论。在课堂上，学生经常会为思维受阻而不能深入学习的时候，有必要组织小组讨论。

2.在知识的转折点处组织合作讨论。

从老到新知识的转折点，学生经常会遇到一些困难和障碍，这时就可以组织团队讨论。

参考文献：

[1]王光明.新版数学课程标准解析与教学指导[M].北京师范大学出版社，2011.

[2]柴林喜.小学数学课堂教学的55个细节[M].四川教育出版社，2006.

[3]孙企平.新课程理念与小学数学课程改革[M].东北师范大学出版社，2002

编辑 李琴芳