基于无量纲的电站加热器变工况建模和研究

于忠平， 胥建群， 黄喜军

(1. 大唐南京发电厂，江苏 南京 210057；2. 东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096)



·发电技术·

基于无量纲的电站加热器变工况建模和研究

于忠平1， 胥建群2， 黄喜军2

(1. 大唐南京发电厂，江苏 南京 210057；2. 东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096)

回热系统是发电机组热力系统重要组成部分，加热器是其主要的辅助设备。传统回热系统加热器变工况运行的数学模型非常复杂，建模过程中涉及流体相变问题。本文基于电站加热器在实际运行中的数据，采用无量纲方法建立加热器运行模型，无需考虑加热器内部复杂的传热过程。将模型用于某660 MW超超临界汽轮机组的低压加热器上，结果表明：利用该模型计算的加热器出口水温和实际测量数据偏差很小；在满足精度要求的情况下，该模型简单方便，工程上可用于回热系统加热器的经济运行指导和故障诊断。

无量纲数；加热器；变工况

0 引言

回热系统是发电厂重要的组成部分之一，回热加热器的作用是利用汽轮机的抽汽提高给水温升，提高平均吸热温度，减少不可逆损失，从而使系统的循环效率增大。因此，对回热系统进行性能分析是保证整个机组经济运行的前提。

回热系统由高压加热器、低压加热器、除氧器、给水泵和凝水泵等设备组成，加热器是回热系统的核心部分。其中，低压加热器与高压加热器的基本结构相同，主要区别在于低压加热器没有过热蒸汽冷却区，只有凝结段和疏冷段。在过热段，过热蒸汽冷却成饱和汽体；在凝结段饱和蒸汽释放汽化潜热冷凝成水；在疏冷段疏水过冷释放热量加热给水[1]。加热器存在相变区导致其运行工况较复杂。目前，有两种较为主流的加热器建模方法。第一种是将加热器看成一个整体，模型包含能量守恒定律和传热方程，通常将传热系数假设为常数或者是关于雷诺数或普朗特数的一个函数，该类模型可以用于参数在一定范围内变化的工况。如王建平等从整体上考虑，建立不同结构加热器动态过程的统一数学模型，但精度较差[2]；宁涛等建立了回热加热器凝结段的理论模型并且用实验验证了模型精度，但该模型单一，只能针对加热器某一区域，求解过程也比较复杂，这类算法很少用于工程上[3]。第二种是将加热器分成二段或三段，每一段应用能量守恒定律和传热方程，单独考虑每一段的传热系数[4,5]，且需要反复迭代求解。有些学者也将加热器变工况的数学模型分成四段或者六段来建模，但这种模型更加复杂[6]。这些加热器的理论模型虽然精度高，但是建模过程复杂，计算量大，不方便求解，很难运用到实际电厂中的现场在线计算；与此同时，考虑到经济原因，实验模型也很难获得。

面对加热器复杂的参数计算，如何在实际电厂有限测点的情况下提高加热器的效率是一个技术难点。为了寻求工程上简单、实用的建模方法，即在保证工程精度情况下，模型能运用于电厂实际运行中的在线计算，本文从实际测量数据出发，基于无量纲数理论建立加热器的变工况数学模型，将无量纲建模方法运用于现场快速计算，实现加热器的故障监测[7-14]。

1 回热系统加热器变工况的数学模型

1.1 系统描述

以某660 MW超超临界汽轮机的第一级低压加热器(LE1)为研究对象，其系统简图如图1所示。

1.2 数学模型的建立

对于表面式加热器，用能量平衡方程描述其传热过程有[15,16]：

Q0=Ch(Th1-Th2)=Cc(Tc2-Tc1)

(1)

C=cpqm

(2)

图1 某电厂回热低压加热器系统Fig.1 Schematic diagram of regenerative low pressure heater system in one power plant

该过程也可以用传热方程描述：

Q0=kAΔTm

(3)

式中：Q0为传热量，J/s；Th1，Th2，Tc1和Tc2分别为第一级低加抽汽温度、疏水温度、进口水温和出口水温，℃；C为热容量，J/(K·s)；cp为比热容，J/(kg·K)；qm为质量流量，kg/s；Ch和Cc分别为加热流体和给水的热容量，J/( kg·K )；k为总传热系数，W/(m2·K)；A为换热面积，m2；ΔTm为对数平均温差，℃。

加热器能效是用来评价一个加热器工作好坏程度指标之一，其是加热器实际热流和最大热流之比，它与加热器的换热面积、总传热系数和换热流体的比热容有关，故加热器的能效表达式可以表示如下[17-21]：

(4)

能效还可以用加热器的温差来表示：

(5)

式中：ε为加热器的能效；Q和Qmax分别为加热器的实际热流和最大热流，J/s；Cmin和Cmax分别为加热器最小热容量和最大热容量，其值介于给水热容量Cc和抽汽热容量Ch之间，J/(K·s)。

对于总传热系数k，它和蒸汽侧换热系数、水侧换热系数、换热管壁厚度和管热管导热系数等因素有关，见式(6)；而求解这些换热系数要用到雷诺数、努塞尔数和普朗特数等与两侧流体的流动状态有关的无量纲数，要求解这些无量纲数必须知道加热器出口温度，故要迭代求解，且不同的流动状态对应不同的无量纲数的求解公式，故通过求解总传热系数来分析加热器的运行状态不仅过程麻烦而且计算量比较大。

(6)

式中：αh为蒸汽侧传热系数，W/(m2·K)；αc为水侧传热系数，W/(m2·K)；δ为换热管壁厚度，m；λ为管热管导热系数，W/(m·K)。

综上所述，加热器的能效主要由换热的流体温度(Tc2，Th1，Tc1)，流体的热容(Ch，Cc)，总传热系数k和换热面积A共同决定：

ε=f1(Tc2,Th1,Tc1,Ch,Cc,k,A)

(7)

式中:f为无量纲函数。

流体的热容量等于定压比热容和流体质量流量的乘积。由上述分析可知，通过总传热系数求解加热器能效的过程是比较麻烦的，故可以通过另一种方法来避免总传热系数的求解，即总传热系数是加热器进口流体温度和流量的函数。所以加热器能效函数(7)可被认为是加热器进口流体温度、流量和换热面积的函数，即关于加热器出口温度的独立变量由7个减少至6个：

ε=f2(Tc2,Th1,Tc1,mh,mc,A)

(8)

由式(5)可知，能效ε与温升(Tc2-Tc1)和(Th1-Tc1)有关，加热器的目的是如何用最小的能耗让加热器产生最大的温差，因此两者之间关系是等效的。故求解能效的过程可以转换成求解加热器给水温升的过程，目的是将式(8)进一步简化：

Tc2-Tc1=f3(Th1-Tc1,mh,mc,A)

(9)

式(9)将独立变量由6个减少至4个，进一步简化了模型，避免大量计算，根据无量纲理论，其可被写成下式：

Tc2-Tc1=C0(Th1-Tc1)a(mh)b(mc)cAd

(10)

其中，C0,a,b,c和d分别为无量纲常数。

比较相关单位的指数，得到上述方程的解：

a=1,c=-b,d=0

(11)

将以上解代入式(10)中可得：

Tc2-Tc1=C0(Th1-Tc1)1(mh)b(mc)-bA0

(12)

整理可得：

(13)

引进无量纲参数Π1：

(14)

式(13)可以通过构造新的函数来求解，即构造关于加热器能效ε和Π2的函数关系式：

(15)

上述分析确立了2个无量纲参数ε和Π1之间的关系，这2个无量纲参数和换热进口流体温度、流量和加热器出口水温相关。实际电厂中不同加热器的测量数据对应不同的具体函数形式。

2 数学模型的实际运用

为进行理论验证，以第一级低压加热器为例，采取设计数据进行研究。首先取TRL、100%、75%、50%、40%设计工况的负荷点数据，参照以上无量纲分析方法进行计算，得出ε和Π1的关系如图2所示。二者成线性关系，用函数可表示为：Π1=0.2745ε+0.0096，R2为函数的确定系数，越接近1表明拟合函数越可靠，R2=0.965表明该拟合函数的精度较高。

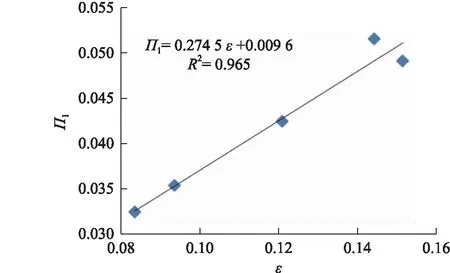
图2 汽轮机组设计数据能效ε和Π1的变化关系Fig.2 The relationship between energy efficiency ε and Π1 of turbine design data

模型运用于实际过程中，需要测量加热器的参数有：加热蒸汽压力和温度，疏水温度，被加热水进、出口水温和流量。根据第一级低压加热器实际运行中的测量参数，采集机组运行一天的数据，计算ε和Π1，并求得2个无量纲数之间的函数关系。所得函数关系如图3所示。二者亦成线性关系，与理论模型验证趋势相一致，但由于实际运行时负荷的变化，如果考虑加以修正，应能得到更好的线性关系。

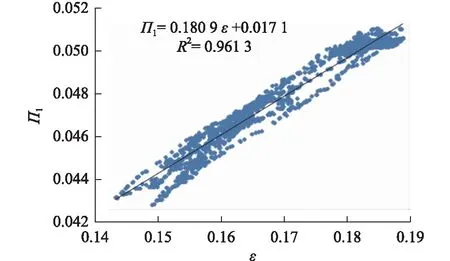
图3 实际运行参数计算的能效ε和Π1的变化关系Fig.3 The relationship between the energy efficiency ε and Π1 of operation parameters

分析实际运行数据和设计数据以及数学模型的偏差，在实际运行中，由于电网调度、煤种变化和运行水位调整等多方面的因素影响，工况在不断变化。低压加热器的流体流量、各运行参数和负荷紧密相关，上述数学模型在实际应用时应考虑负荷的修正，因此式(12)中的常数C0引用成和负荷成关系的数，这样可以得到：

(16)

式中：P为实际负荷，kW。

用实际数据计算，得出该函数关系，如图4所示，二者线性相关性较强，将数据拟合近似关系式：

(17)

图4 负荷/(ε/Π1)随负荷的变化关系Fig.4 The alternative relation of Load / (ε/Π1) with the change of load

如果用该公式来计算第一级低压加热器出口温度，和实际温度对比，计算值和测量值的误差很小，最大误差为+0.15%。为验证修正关系的正确性，用该修正后的低加出水温度修正公式来计算另外一天的第一级低加出水温度，且未去除工况变化剧烈点，具体结果如图5所示。图中显示修正后的计算公式在机组50%～100%负荷区域内变化时，和实际测量数据拟合度基本一致，绝对误差范围在-1.8～1.2 ℃之间，相对误差范围在-0.012%～0.008%之间，满足工程误差要求。

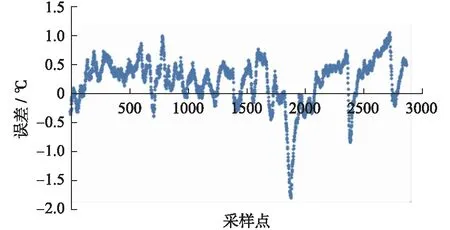
图5 另一天低加出口温度的计算值和测量值的偏差Fig.5 The deviation of the calculated and measured values of low pressure heater outlet temperature in another day

3 无量纲数应用于加热器数学模型研究的推广意义

基于无量纲方法建立的数学模型在模拟电站加热器实际运行时的变工况误差很小，可以利用该方法进行运行指导和故障分析诊断，如运行中的水位调整、监测加热器泄漏、加热器传热效果以及汽水侧阀门状态等。根据实际测量数据和模型计算数据的偏差分析诊断故障类型，提前做好谋划，利用机组检修时间进行确认并整治，提高电站回热效率。如加热器轻微泄漏时，会导致水侧流量低，出水温度偏高，进汽量和疏水量都减少。在实际运行中应注意测量数据的收集计算分析，和新机组或设计数据建立的模型比较分析，及时发现问题。

4 结语

电站回热系统加热器实际变工况运行的模型建立非常复杂，为获得简单易算且精度能够满足要求的电站加热器变工况数学模型，本文基于无量纲方法利用实际变工况运行数据建立电站加热器的运行模型；利用该模型计算的加热器运行数据和实际测量数据偏差很小，相对误差最终控制在0.15%范围内。该模型简单易算，工程上可用于运行指导和加热器设备故障诊断，对提高电站回热系统效率有重要意义。

[1] 杨 涛,胥建群,周克毅,等. 电站给水加热器水位的优化运行[J]. 东南大学学报(自然科学版), 2012, 42(S2): 314-319. YANG Tao, XU Jianqun, ZHOU Keyi,et al. Optimal of feedwater heater liquid level in power plant[J]. Journal of Southeast University(Natural Science Edition), 2012,42(S2): 314-319.

[2] 王建平,陈 红,王广军. 火电厂回热加热器全工况建模与仿真[J]. 计算机仿真,2006,23(5):220-223. WANG Jianping, CHEN Hong, WANG Gugangjun.Overall performance modeling and simulation of regenerative feed water heater in power plant[J]. Computer Simulation,2006,23(5):220-223.

[3] 宁 涛,张瑞山,李 根,等. 纯凝结段回热加热器动态特性研究[J]. 工程热物理学报,2013,24(4):676-679. NING Tao, ZHANG Ruishan, LI Gen, et al. The dynamic behavior research on feedwater heater with condenser zone[J]. Journal of Engineering Thermophysics, 2013,24(4):676-679.

[4] 李秀云,严俊杰,林万超. 具有蒸汽冷却器的回热加热器变工况特性研究[J]. 中国电力,2001, 24(1): 25-28. LI Xiuyun, YAN Junjie, LIN Wanchao.Research on variable load operation performance of regenerative heater with superheated steam collector[J]. Electric Power, 2001,24(1):25-28.

[5] 赵文升,王兵树,马良玉,等. 大型火电机组加热器动态数学模型的研究[J]. 汽轮机技术, 2001, 43(6): 324-327. ZHAO Wensheng, WANG Bingshu, MA Liangyu, et al. Research on dynamic mathematical model of the heater for large thermal power unit[J]. Turbine Technology, 2001, 43(6): 324-327.

[6] BARSZCZ T, CZOP P, A feedwater heater model intended for model-based diagnostics of power plant installations[J]. Applied Thermal Engineering, 2011, 31: 1357-1367.

[7] 陈华桂,卢承斌. 600 MW机组高排蒸汽参数异常升高原因分析与现场处理[J]. 江苏电机工程,2016,35(1):89-91. CHEN Huagui, LU Chengbin. Analysis and on-site treatment of abnormal exhaust steam parameter increase in HP cylinder of 600 MW power unit[J]. Jiangsu Electrical Engineering, 2016, 35(1): 89-91.

[8] 万 跃,晏海能. 汽轮机疏水系统优化节能改造[J]. 江苏电机工程,2014,33(6):79-81. WAN Yue, YAN Haineng. Energy saving transformation of draining system of steam turbines[J]. Jiangsu Electrical Engineering, 2014, 33(6): 79-81.

[9] 于爱萍. 核电机组二回路低加液位调节优化过程分析[J]. 江苏电机工程,2015,34(2):52-54, 57. YU Aiping. Optimization analysis of level controller for low pressure heat-exchanger in secondary loop of nuclear units[J]. Jiangsu Electrical Engineering, 2015,34(2):52-54+57.

[10] 张 晓,李录平,陈腊民,等. 加热器内部泄漏故障的实验研究[J]. 热能动力工程,2011,26(1):63-66+123. ZHANG Xiao,LI Luping, CHEN Lamin, et al. Experimental study of inner leakage accidents of a heater[J]. Journal of Engineering for Thermal Energy and Power,2011,26(1):63-66, 123.

[11] 李 刚,胥建群,汤 涛,等. 汽轮机通流效率与机组热耗率关系的计算[J]. 江苏电机工程, 2014, 33(4): 13-16. LI Gang, XU Jianqun, TANG Tao, et al. The relationship between flow path performance and heat consumption rate of steam turbine[J]. Jiangsu Electrical Engineering, 2014,33(4):13-16.

[12] 孙成林. 火力发电厂电气设备状态检修[J]. 江苏电机工程,2014,33(4):81-84. SUN Chenglin. The condition-based maintenance of coal-fired power plant electrical equipment[J]. Jiangsu Electrical Engineering, 2014,33(4):81-84.

[13] 裴宜星,王 江,吴 帆. 核电站高压加热器泄漏仿真[J]. 计算机仿真,2013,30(8):139-142. PEI Yixing, WANG Jiang, Wu Fan. High pressure feed-water heater leakage simulation in nuclear power simulator[J]. Computer Simulation,2013,30(8): 139-142.

[14] 钱宇峰. 某600 MW机组低压加热器疏水不畅原因分析及处理[J]. 江苏电机工程,2012,31(1):72-74. QIAN Yufeng. Analysis and disposal of low pressure heater drainage issues in 600 MW power plant[J]. Jiangsu Electrical Engineering, 2012,31(1): 72-74.

[15] 沈维道,童钧耕. 工程热力学[M]. 北京：高等教育出版社,2007:52-56. SHEN Weidao, TONG Jungeng. Engineering thermodynamics[M]. Beijing: Higher Education Press, 2007:52-56.

[16] 杨世铭,陶文铨. 传热学[M]. 北京：高等教育出版社,2006:5-6. YANG Shiming, TAO Wenxuan. Heat transfer[M]. Beijing: Higher Education Press,2006: 5-6.

[17] 杨 涛,胥建群,周克毅,等. 基于量纲分析的加热器变工况特性计算模型[J]. 汽轮机技术, 2013, 55(5): 326-330, 334. YANG Tao, XU Jianqun, ZHOU Keyi, et al. Varying condition characteristic calculation model of feedwater heater based on dimensional analysis[J]. Turbine Technology, 2013, 55(5): 326-330, 334.

[18] LASKOWSKI R, LEWANDOWSKI J. Simplified and approximated relations of heat transfer effectiveness for a steam condenser[J]. Journal of Power Technologies, 2012, 92(4): 258-265.

[19] NAKAYAMA Y, BOUCHER R. Introduction to fluid mechanics[M],1999: 238-273.

[20] LASKOWSKI R. The application of the buckingham Π theorem to modeling high-pressure regenerative heat exchangers in off-design operation [J]. Journal of Power Technologies, 2011, 91(4): 198-205.

[21] 杨 波,李 政. 火电机组热力系统主导因素变工况建模方法研究[J]. 中国电机工程学报,2005, 25(24): 96-102. YANG Bo, LI Zheng. Dominant factor modelling method for the thermal system of power station[J]. Proceedings of the Chinese Society for Electrical Engineering,2005,25(24):96-102.

(编辑 刘晓燕)

Modeling of Regenerative Heater of Off-design ConditionsBased on Dimensionless Method

YU Zhongping1, XU Jianqun2, HUANG Xijun2

(1. Datang Nanjing Power Plant, Nanjing 210057, China; 2. Key Laboratory of Energy Thermal Conversion and Control,Ministry of Education,Southeast University, Nanjing 210096, China)

Regenerative system is an important part of steam turbine system in power plant. The regenerative heaters models in off-design conditions are very complicated due to the heaters phase-change problem. A dimensionless model for regenerative heater is built up according to actual measurements which reflects its operation status in off-design conditions. This model is applied to the first low-pressure heater of a 660 MW ultra-supercritical steam turbine unit. Results show that the deviation of model calculation results and actual data are very small. The modeling method is simple and credible and can be used as tools for practical troubleshooting in power plant.

dimensionless parameter；regenerative heater；off-design conditions

2017-02-05；

2017-04-01

TK267

A

2096-3203(2017)04-0150-05

于忠平

于忠平(1982-)，男，江苏南京人，助理工程师，从事电厂汽机检修与维护工作(E-mail:496355441@qq.com);

胥建群(1959—)，男，陕西汉中人，教授，长期从事电站性能分析、仿真建模和分布式能源系统教学与研究工作(E-mail:qlj1062@163.com);

黄喜军(1991—)，男，广西南宁人，在读硕士，研究方向为火电机组性能分析与控制(E-mail:71956604@qq.com)。