基于统计的我国短时交通流预测模型分析

王晓丹，白云,，李川

（1.重庆工商大学电子商务及供应链系统重庆市重点实验室，重庆 400067；2.重庆工商大学国家智能制造服务国际科技合作基地，重庆 400067）

基于统计的我国短时交通流预测模型分析

王晓丹1，白云1,2，李川2

（1.重庆工商大学电子商务及供应链系统重庆市重点实验室，重庆 400067；2.重庆工商大学国家智能制造服务国际科技合作基地，重庆 400067）

短时交通流量预测作为交通控制管理、交通诱导提供技术支持之一，已经成为交通工程的研究热点。为了研究近年来预测模型的现状，在中国知网数据库高级检索功能中以“篇名：短时交通并含预测”和“发表时间：2000-2016”为条件进行检索，共检索到133篇核心期刊。通过对期刊的分类统计，就当前国内常用的预测模型的原理及作用作简单介绍，并根据现有各模型的优缺点和使用范围，对未来的发展趋势做初步探讨。

0 引言

交通控制与道路诱导系统是智能交通系统建设的核心内容，而实现该系统的关键是实时准确的短时交通流量预测。一般认为短时交通流预测就是根据已有的交通流数据，在时刻实时预测出下一时刻t+△t的交通流量，其中△t一般在5-15min内（甚至小于5min）。短时交通流预测常用于交叉路口信号实时优化、交通控制、交通诱导等方面，具有强烈的非线性、时变性、随机性以及与上游路口交通流的相关性等特点。为了研究近年来预测模型的现状，在中国知网数据库高级检索功能中以“篇名：短时交通并含预测”和“发表时间：2000-2016”为检索条件进行检索，共检索到133篇核心期刊。其中每年核心期刊数量分布如图1。

从图1可以看出，2000-2006年间，专家和学者对短时交通流的研究较少。从2007年之后，文献数量成明显增长趋势，说明越来越多的人关于短时交通流预测。基于收录的文献内容来看，可以分为综述和和学术论文；统计结果显示，综述是4篇，占总文献数量的3.01%；学术论文是129篇，占总文献数量的96.99%，由此可以看出，短时交通流预测模型的建立已经逐渐成为交通管理领域研究热点。

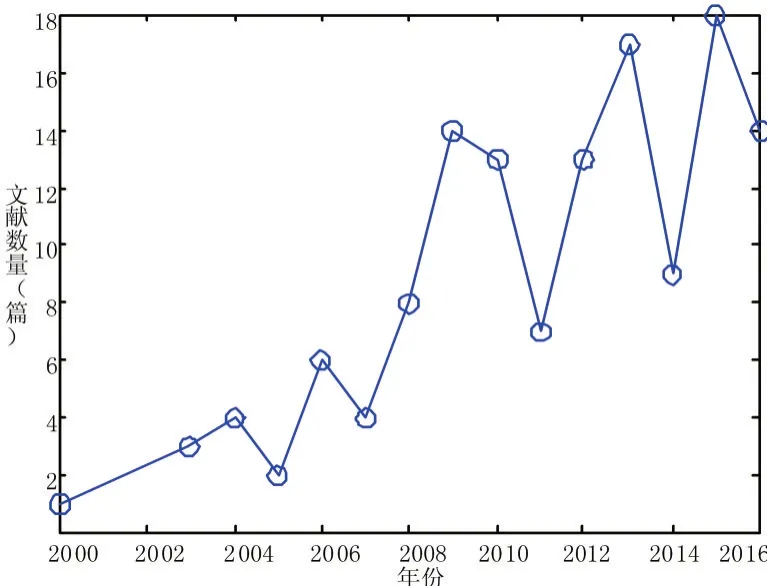
图1 历年关于短时交通流预测核心期刊数量

1 短时交通流预测模型分类

从20世纪60年代开始，人们就开始把其他领域成熟的预测模型用于短时交通流预测，并开发了多种预测模型与方法[1]，大致分为四类[2]：线性模型、非线性模、组合模型(各模型数量如表1所示)。从表1可以看出非线性模型占比最高，占49.61%；其次是组合模型，占比为37.98%；组合模型和非线性模型共占88.60%，文献占比最多。

表1 各预测模型文献数量及占比

如图2所示，可以看出非线性和组合模型研究呈增长趋势，说明组合模型和非线性模型预测短时交通流是研究重点。非线性模型在处理非平稳、高波动数据方面所表现的能力，已经成为了预测交通流量的热点，同时相比较时间模型也呈现出较好的预测精度[3]。

图2 各预测模型每年核心期刊数量

根据对核心期刊的分析，把排名靠前的预测模型统计出来，其结果如图表2所示。在之后章节对这几种预测方法进行详细介绍。从统计结果来看，大量的优化算法广泛应用到非线性模型优化参数方面，如粒子群算法、蚁群算法、遗传算法、混合蛙跳算法等。

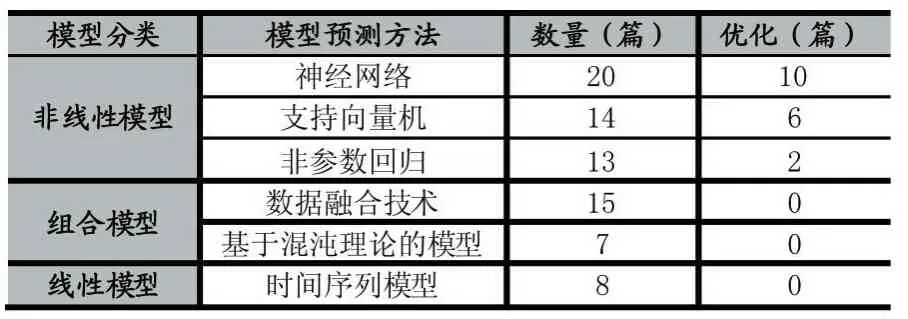
表2 各类模型预测方法文献数量

2 基于线性系统理论预测模型

线性模型是通过分析事物的运动规律和改变这种规律的因素和方法，来揭示各因素之间，参数和性能间确定的和定量的关系。由于短时交通流具有较强的实时性和随机性的特点，因此计算复杂度较低，操作简单的线性模型满足不了预测结果精度较高和动态反馈性的要求。

时间序列模型是参数化模型处理动态随机数据的常用方法之一，不仅考虑了观测数据在时间序列上的依赖性，同时也考虑了随机波动的干扰性。在短时交通流预测模型中，广泛使用的平稳模型是自回归求和滑动平均模型（ARIMA模型）。针对ARIMA模型中存在的缺点，如没有考虑外部其他因素的影响，检验过程中模型定阶及参数估计繁琐，模型参数无法动态调整以及需要大量的样本支持等缺陷，很多学者进行不同的探索，如唐毅等[13]通过动态选择适宜的样本序列和直接使用ARIMA(p,d,0)模型，来消除模式识别的不确定性和进行时间序列模型的优化；常刚等[4]构建了一个基于时空依赖性的自回归差分移动平均模型（STARIMA模型）。邴其春等[5]为了降低参数估计的误差，提出了一种基于时间序列——向量误差修正模型的短时交通参数预测模型。

3 基于非线性理论的预测模型

早期的线性模型往往不能适应短时交通流非线性数据的预测要求，越来越多的非线性预测模型应用到短时交通流预测模型中去，并取得了较好的预测效果。人工神经网络是由大量神经元的以某种拓朴结构相互连接而成的非线性系统，它是在对以人脑为代表的生物神经元系统的组织结构和行为特征进行研究的基础上提出的。现实任务中使用神经网络时，大多是使用误差逆传播算法进行训练，其网络拓扑结构如图3，其中V和W是连接权值，其中隐含层数可根据实际预测需要进行添加。因此，在构建神经网络模型时，应先通过一部分数据测试输入，输出和隐含层神经元个数，各层连接权以及各神经元的传递函数，从而确定网络结构，再用剩余的数据进行预测。

从模型建立来看，基于神经网络的“黑箱”学习模式，不需要大量的经验方式，只需要大量的数据支撑，就能获得这些数据的运动规律。其高度的非线性映射及全局表现能力、良好的容错性与联想记忆功能、优秀的自适应、自学习等功能，适合短时交通流预测领域广泛应用[16-18]。但是神经网络存在过拟合现象，陷入局部最小、收敛速度过慢等问题，针对这些问题，一些学者通过各种算法[6]来优化连接权值和阈值，或者优化局部搜索能力来优化模型。神经网络能够能够较好地运用于短时交通流的预测，但大多数是验证性研究，即预测方法能完成预测并与其他方法进行对比，没有指出神经网络的适用范围和应用条件。小波神经网络是结合小波变换理论与神经网络的思想而构造的一种新的神经网路模型。用小波基函数代替隐含层中神经元的激励函数，这充分继承了小波变换良好的时频局部化性质及神经网络的自学习功能的特点，具有最佳的函数逼近能力，能有效克服普通人工神经网络固有的缺陷，用其建立的模型可以取得更好的预测效果[7]。

图3 BP神经网络拓扑结构图

支持向量机是基于统计学习理论的VC理论的新一代机器学习方法，通过寻求结构化风险最小来提高学习泛化能力，从而在统计样本数量较少的情况下，仍能获得较好的统计规律。SVM模型属于参数预测方法，在预测过程会存在核函数选择，参数和特征集优化等问题，一些学者和专家在这方面进行了优化。大量的实验证明，预测精度方面，支持向量机相比较神经网络和传统的预测方法具有明显的优势[8]。支持向量机能够解决“多维灾难”，样本数量小和解决局部最优问题，正成为预测应用热点。

非参数回归模型是以模式识别方法为技术，不需要先验知识，通过大量历史样本库中找到一组与输入数据相对应的目标数据来进行预测。其具有算法清晰、可移植性强、预测精度高的、时间强壮性强，误差比较少且分布良好等优点。但在实际应用中，仍存在搜集历史数据难、处理历史数据复杂、最近邻查找效率较低、没有反馈回路、预测算法不够合理等问题。针对非参数回归在短时交通流预测上的局限性，张晓利[9]、于滨[10]和谢海红[11]等分别在利用反馈机制、考虑时空参数、修改搜索方法等方面进行了改进。

4 组合模型预测

为了有效地利用各种模型的优点，Bates等于1969年提出混合预测的思想，将参与组合的各种预测方法通过适当的方式组合或者对预测结果进行适当的加权，“取长补短”，获得最优的预测结果[12]，一般是线性方法与非线性方法，非线性方法之间的组合。组合模型在一定程度能提高预测模型的精度，但是以牺牲模型的预测速度为代价，同时也增加了模型的复杂度。

数据融合技术是对各模型预测结果的融合，它的最大优势在于能合理协调多元数据[13]，其流程图如图4，对于不在阈值范围内的交通流数据进行处理，选择n种成熟度较高和预测精度较高的方法进行预测，动态确定最优权重进行融合来获得最终结果。但也存在最优权重系数的确定、模型复杂、融合后的数据处理量加大、运算能力减弱等问题。

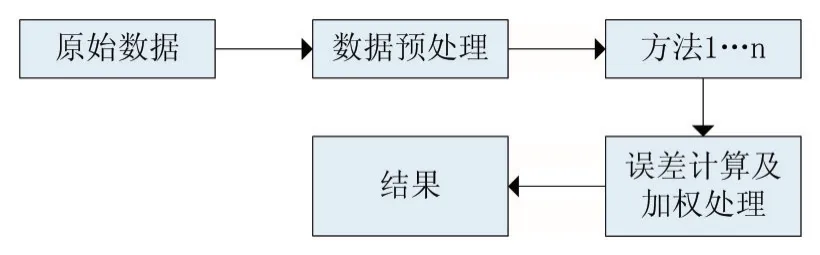
图4 数据融合技术流程图

混沌理论是近年来发展的一门新兴学科，兼具质性与量化分析的方法，用于探讨非线性动态学系统的内在随机性。Laypunov指数是混沌系统的吸引子的宏观特征量之一，同时也是判断一个动力学系统可预测性及预测时间跨度的重要指标。在进行交通流混沌特性的判断之前，先利用相空间重构技术把一维时间序列映射到高维空间，从而在高维空间中计算Laypunov指数，来描述其中所蕴藏的内在变化规律。基于混沌理论的神经网络预测模型，通常先通过相空间重构来对交通流数据进行预处理，计算出嵌入维数作为神经网络的输入节点数，再用训练好的神经网络对时间序列进行预测，实验证明，其预测结果明显好于单一的神经网络预测模型[15]。

5 结语

通过对以上模型的分析，可以看出每一种预测模型都在一定条件下具有明显的优势，同时也存在着不足，所以在模型选择时要根据不同的环境、不同的样本数据来选择预测模型。从统计结果来看，短时交通流预测的发展方向会倾向于非线性模型的运用和对其的优化；同时，随着云计算、大数据时代的到来和计算机能力的大幅度提高可缓解训练低效性，训练数据的大幅度增加则降低过拟合风险，以组合模型为代表的复杂模型的创新会得到人们的广泛关注。

[1]沈国江，王啸虎，孔祥杰．短时交通流量智能组合预测模型及应用[J]．系统工程理论与实践，2011，31(3):561-568．

[2]陆海亭，张宁，黄卫，等．短时交通流预测方法研究进展[J]．交通运输工程与信息学报，2009，7(4):84-91．

[3]谢海红，戴许昊，齐远．短时交通流预测的改进K近邻算法[J]．交通运输工程学报，2014，14(3):87-94

[4]常刚，张毅，姚丹亚．基于时空依赖性的区域路网短时交通流预测模型[J]．清华大学学报(自然科学版)，2013，53(2):215-221．

[5]邴其春，杨兆升，周熙阳，等．基于向量误差修正模型的短时交通参数预测[J]．吉林大学学报(工学版)，2015，45(4):1076-1081．

[6]李松，刘力军，翟曼．改进粒子群算法优化BP神经网络的短时交通流预测[J]．系统工程理论与实践，2012，32(9):2045-2049．

[7]万李，杨杰．小波神经网络在短时交通流量预测中的应用[J]．计算机仿真，2012，29(9):352-355．

[8]王少华，杨慧慧．基于优化参数的短时交通流预测仿真研究[J]．计算机仿真，2015，3(6):167-171，270．

[9]张晓利，陆化普．非参数回归方法在短时交通流预测中的应用[J]．清华大学学报(自然科学版)，2009，49(9):1471-1475．

[10]于滨，邬珊华，王明华，等．K近邻短时交通流预测模型[J]．交通运输工程学报，2012，12(2):105-111．

[11]谢海红，戴许昊，齐远．短时交通流预测的改进K近邻算法[J]．交通运输工程学报，2014，14(3):87-94．

[12]顾晨阳，罗熹，程文龙．变权重组合预测模型在短时交通流预测中的应用[J]．统计与决策，2010(6):168-169．

[13]钱伟，杨矿利，杨慧慧，等．基于组合模型的短时交通流预测[J]．计算机仿真，2015，32(2):175-178，193．

[14]蒋亚平，郭俊亮，赵军伟．基于组合模型的短时交通流预测[J]．现代计算机，2013，(7):26-29．

[15]郭雪峰．基于数据融合的短时交通流预测与智能交通信号系统的研究[D]．湘潭大学，2007．

Analysis of Short-Term Traffic Flow Forecasting Model Based on Statistics in China

WANG Xiao-dan1，BAI Yun1，2，LI Chuan2
(1.Chongqing Key Laboratory of Electronic Commerce and Supply Chain System,Chongqing Technology and Business University,Chongqing 400067；2.National Research Base of Intelligent Manufacturing Service,Chongqing Technology and Business University,Chongqing 400067)

Short-term traffic forecasting which is one of the key technologies of intelligent traffic control management and traffic guidance,has be⁃come a hot topic in the field of traffic engineering.In order to study the status quo of the forecasting model in recent years,a total of 133 code journals were retrieved in the advanced search function of the China Knowledge Infrastructure database,which was searched by"title:Short-term traffic and forecast"and"published time:2000-2016".Based on the classification statistics of journals,this article made a briefly introduction on the principle and function of the current forecasting domestic forecasting models.Future,the future development trend also been preliminary discussed based on current advantages,disadvantages and application range of each model.

重庆市科委基础与前沿研究项目（No.cstc2015jcyjA70007）、重庆市研究生教改项目（No.YJG43015）、国家智能制造服务国际科技合作基地开放基金（No.ghjd201603）

王晓丹（1988-），女，河南商丘人，硕士研究生，研究方向为交通智能预测

2017-03-28

2017-06-02

1007-1423（2017）17-0031-04

10.3969/j.issn.1007-1423.2017.17.006

智能交通系统;短时交通流;预测模型

白云（1985-），男，山西阳泉，博士研究生，助理研究员，研究方向为智能交通管理

李川（1975-），男，重庆市人，博士研究生，研究员，研究方向为智能制造服务

Intelligent Transportation System;Short-Term Traffic Flow;Prediction Model