基于惯性系的旋转式惯导系统快速对准算法*

陈敬萱, 程旭红， 李 晋

(1.哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001；2.烟台广电信息网络中心 广电技术部，山东 烟台 264000)



基于惯性系的旋转式惯导系统快速对准算法*

陈敬萱1, 程旭红2， 李 晋1

(1.哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001；2.烟台广电信息网络中心 广电技术部，山东 烟台 264000)

针对船舶大幅角晃动和线运动等复杂干扰，导致旋转式捷联惯导系统初始对准性能下降的问题，设计了基于惯性系的旋转式捷联惯导系统快速初始对准算法。针对旋转式捷联惯导系统的误差特性，设计了基于惯性系的粗对准方案；并提出了一种改进的罗经对准算法，达到缩短对准时间和提高对准精度的目的。仿真实验证明：该方法可以实现快速初始对准，7 min航向精度达到1.35＇。

捷联惯导系统； 旋转调制； 惯性系； 初始对准； 罗经

0 引 言

海洋多变工况使船舶等运载体所受干扰复杂，导致捷联惯导系统(SINS)难以通过初始对准抑制初始姿态误差。旋转式捷联惯导系统虽然能通过旋转调制实现器件误差抑制，但无法抑制具有初始姿态误差激励的导航误差，因此，初始对准技术仍然是旋转式捷联惯导系统的关键技术之一[1]。

旋转式捷联惯导通常采用粗对准获取粗略姿态矩阵，在此基础上通过精对准获取精确姿态矩阵。然而在大幅摇摆和晃动状态下，地球自转角速度远远小于由于风浪和浪涌干扰引起的干扰角速度，使得传统解析法粗对准[2]无法从陀螺仪输出中敏感给出地球自转角速率信息，从而使粗对准结果误差很大,甚至不可用。文献[3]提出了一种“水平调平+方位估算”粗对准方法，该方案系泊条件下水平对准精度较高，满足粗对准要求，但航向角估算结果不稳定。文献[4]提出了一种基于惯性系的捷联惯导系统粗对准方法，可以很好地隔离载体晃动干扰，但无法抑制惯性器件误差。文献[5]提出的罗经回路法抗干扰特性较好，然而对准时间较长，无法满足初始对准快速性要求。文献[6]提出了适用于旋转式捷联惯导的罗经精对准方法，可以在静态条件下消除方位角常值误差，但未考虑晃动基座条件下对准情形。文献[7]设计了时变参数下的罗经对准方案，可以较好地缩短方位对准时间，但未能解决大幅摇摆和晃动初始对准问题。

基于此，本文提出了一种基于惯性系的旋转式捷联惯导快速罗经对准方法，基于惯性系的粗对准方法，有效地隔离载体由于晃动引起的干扰，从而求出相对精确的初始姿态矩阵；通过罗经对准参数配置优化改进，提高了系统的跟踪性能和抗干扰能力，从而实现缩短对准时间和提高对准精度的目标。

1 坐标系定义

初始对准涉及的常规坐标系，如地心惯性坐标系(i系)、地球坐标系(e系)、导航坐标系(n系)、船体坐标系(b系)，与现有文献定义相同，需特殊定义的坐标系如下：

1)旋转坐标系(s系)：坐标系原点位于船舶重心，初始时刻oxs轴与oxb轴平行，oys轴与oyb轴平行，ozs轴与oxsys平面垂直。

2)初始时刻惯性坐标系(i0系)：在初始对准起始时刻(即当t=t0=0时)，oxi0轴在当地子午面内且平行于赤道平面，ozi0轴指向地球自转方向，3轴构成右手坐标系，初始对准开始后i0系3轴方向相对惯性空间保持不动。

3) 基座惯性坐标系(ib0系)：在t0时刻ib0系重合于b系，初始对准开始后ib0系不随捷联惯导转动，即在惯性空间中保持指向不变。

2 旋转式捷联惯导系统粗对准设计

(1)

(2)

式中

(3)

(4)

式中L0为对准起始t0时刻的纬度。

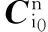
(5)

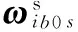
(6)

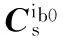
(7)

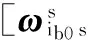
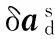
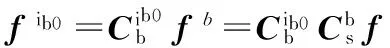
(8)

(9)

对上式两边同时积分，得

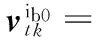
(10)

式中 ΔA被旋转调制成周期性变化量，其在转动周期内的积分均值为0。考虑到近似为周期变化，经过一个周期的积分后产生速度误差近似为0，即

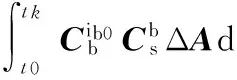
(11)

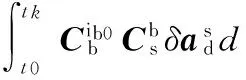
(12)

则式(10)可近似写为

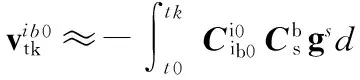
(13)

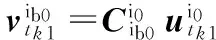
(14)

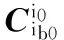
3 旋转式捷联惯导系统精对准设计

3.1 罗经水平对准

罗经水平控制回路如图1所示。

图1 捷联惯导罗经水平对准东向通道

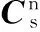
小角度条件下，水平东向对准通道的调节参数传统选取方法如下

Ke1=3σ

(15)

Ke3=σ3/gnξ2

(16)

(17)

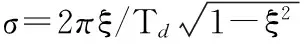
3.2 罗经方位对准

罗经方位控制回路如图2所示。

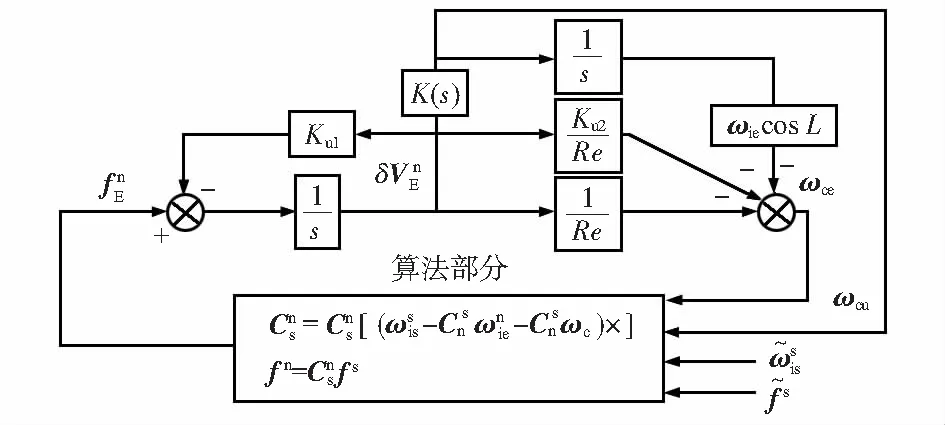
图2 捷联惯导罗经方位对准通道

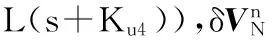
实际设计的罗经方位对准参数一般遵循如下原则：1)为保证在短时间内产生多次振荡，需要提高系统的开环增益和自然频率，从而增加系统刚度，减少系统误差；2)为使系统快速达到稳定状态，需要进行合理的极点参数配置，给对准回路提供适当阻尼，使振荡能量快速衰减。

3.3 罗经对准极点配置

由图2和梅森增益公式，可以得到旋转式捷联惯导罗经回路的特征方程为

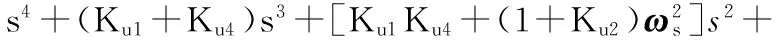
(18)

为一个4阶系统，传统的参数配置将罗经回路假设为由2个相同的振荡环节组成，这种方法组成的2个二阶系统都是振荡环节，在相同的阻尼比条件下，超调量大，稳态对准精度差，尤其是在系泊条件下，船舶产生大幅摇摆，其对准结果将产生较大误差。

为此，将罗经回路由一个振荡环节和一个过阻尼环节组成，且负实轴上的2个极点在以ωn为半径的圆上，即

(19)

令式(19)与式(18)对应项相等，得到各参数如下

Ku1=2ωn

(20)

Ku2=2σ2/(ξωs)2-1

(21)

Ku3=σ4/gnξ2

(22)

Ku4=2σ

(23)

上述方法引入振荡环节来提供较快的响应速度，通过加入过阻尼环节提高系统的稳态精度，在响应速度和稳态精度方面都得到了良好的改进。在摇摆基座条件下，能够提高精对准的精度和快速性。

4 仿真验证

4.1 仿真条件设置

设单轴旋转机构的旋转速度为2°/s，陀螺常值漂移为0.01°/h，陀螺随机漂移为0.001°/h。加速度常值零偏为100 μgn，随机零偏为10 μgn。设船舶大幅摇摆的纵摇角θ,横摇角γ,航向角ψ,规律为：θ=10°sin(2πt/12+φθ)，γ=12°sin(2πt/10+φγ)，ψ=7°sin(2πt/15+φψ)，初始相位φθ,φγ,φψ，分别为[0,2π]上服从均匀分布的随机相位。同时纵荡、横荡和垂荡引起线干扰,线运动干扰速度设为VDi=ADiωDicos(ωDit+φDi),i=e,n,u，ADe=0.02m，ADn=0.03m，ADu=0.5m′，ωDi=2π/TDi，TDe=9 s，TDn=10 s；φDi为[0,2π]上服从均匀分布的随机相位。

4.2 仿真结果分析

1)惯性系粗对准仿真

为验证惯性系粗对准方法性能，选取“水平调平+方位估算”法,SINS惯性系粗对准方法作为比较，分别对上述3种方法进行粗对准仿真。

选取粗对准时间为120 s，tk1=60 s，tk2=120 s，进行100次仿真。统计100次粗对准结果，表1为120 s时刻3种粗对准方法结束时刻得到的3个方向的姿态误差角的最大值和均值，并以此作为粗对准精度的衡量指标。

表1 粗对准仿真结果统计(均值)

由表1分析可知，3种粗对准方法对准之后系统水平角误差皆在10′以内。然而，对于方位对准性能，“水平调平+方位估算”法方位对准精度均值达到1.53°，最大值高达4.63°，无法实现对准误差小角度的实际需求。基于惯性系的粗对准方法120 s时刻方位对准精度在1°以内。本文提出的惯性系粗对准引入旋转调制系统以后，可以抑制惯性器件漂移对初始对准精度的不良影响，在惯性系粗对准的基础上，进一步提高了方位对准精度，证明了方案的有效性。

2)改进罗经法精对准

对比传统罗经法、改进的罗经法、旋转调制+传统罗经法和旋转调制+改进罗经法4种算法在系泊干扰条件下的初始对准效果。

以惯性系粗对准法中100次仿真结果中的最大值作为精对准的初始失准角，每组仿真时间为300 s。4种精对准方案的仿真结果如图3所示，各精对准算法的性能指标如表2所示。

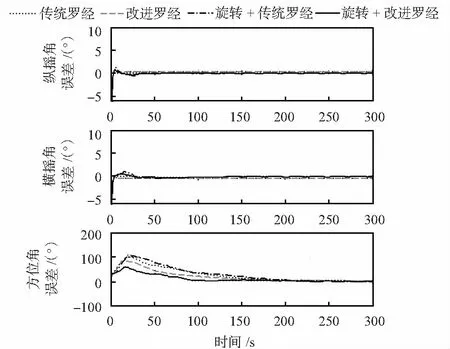
图3 精对准仿真结果

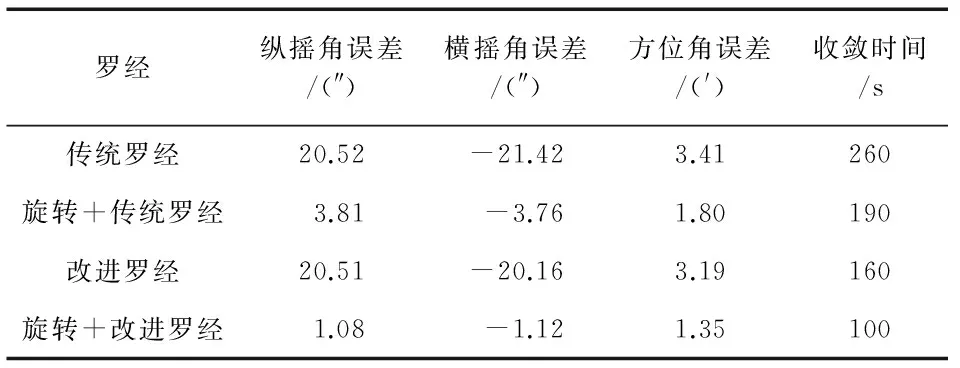
罗经纵摇角误差/(″)横摇角误差/(″)方位角误差/(')收敛时间/s传统罗经20.52-21.423.41260旋转+传统罗经3.81-3.761.80190改进罗经20.51-20.163.19160旋转+改进罗经1.08-1.121.35100

由图3和表2可知，改进的参数配置罗经法与传统的方法相比，水平对准精度基本相当，方位精度要优于传统方法，旋转调制+改进罗经法最终对准精度可达到1.35′。此外，对于初始对准时间，由图3和表2可知，本文提出的改进的旋转式捷联惯导罗经对准方法，在保证对准精度性能提升的前提下，较其他3种传统的对准方法显著地缩短了对准时间，可以实现100 s时刻方位角误差收敛至10′以内。

5 结 论

针对大幅角晃动和线运动等复杂干扰下的旋转式捷联惯导初始对准，设计了基于惯性系的粗对准方案，以及改进罗经对准法，在提高精对准精度的前提下，缩短了精对准结果的收敛时间，实现快速罗经精对准。仿真实验结果表明：新方法可以很好地实现复杂干扰下的初始对准，有效提高了系统对准性能，对工程应用具有一定参考价值。

[1] 迟风阳,孙 枫,徐 博.迭代容积粒子滤波算法在SINS初始对准中的应用[J].传感器与微系统,2013,32(7):136-140.

[2] 魏春玲,张洪钺.捷联惯导系统粗对准方法比较[J].航天控制,2000,18(3):16-21.

[3] 高 伟,陆 强,高 洁,等.水下潜器捷联惯导系统初始对准技术研究[J].中国航海,2003,56(3):5-8.

[4] 秦永元,严恭敏,顾冬晴,等.摇摆基座上基于信息的捷联惯导粗对准研究[J].西北工业大学学报,2005,23(5):681-684.

[5] Sandoval-Romero G E.Fiber-optic gyrocompass super-luminescent fiber source[J].IEEE A&E Systems Magazine,2005,20(7):19-20.

[6] 杜红松,牟宏杰,程建华.四陀螺冗余配置的单轴旋转调制捷联惯导方法[J].传感器与微系统,2016,35(11):64-67.

[7] 郝燕玲,张 义,孙 枫.航向大失准角下的罗经对准算法[J].仪器仪表学报，2011，32(7)：1478-1483.

[8] 尚松田,付梦印,刘 彤.单轴旋转式捷联惯导系统转位方案[J].北京理工大学学报,2011,31(11):1318-1321.

[9] 管 斌,王成宾.序贯抗差估计在旋转调制陀螺寻北中的应用[J].传感器与微系统,2014,33(12):158-160.

Rapid alignment algorithm for rotary INS in inertial frame*

CHEN Jing-xuan1, CHENG Xu-hong2, LI Jin1

(1.College of Computer Science and Technology,Harbin Engineering University,Harbin 150001,China;2.Broadcast Department,Yantai Broadcast and Television Information Network Ltd,Yantai 264000,China)

Complex interference of angular swaying and linear motion can depress the alignment performance of the rotary strapdown inertial navigation system(SINS).In order to solve the problems,a rapid alignment algorithm for rotary SINS in inertial frame is presented.Based on error characteristics of rotary SINS,design a coarse alignment method in inertial frame.And an improved rotary SINS gyrocompass alignment algorithm is proposed to speed up the alignment and increase precision.Simulation results show that the proposed algorithm can accomplish Rotatry SINS alignment quickly,and make azimuth accuracy confine to 1.35 minute of arc in 7 min.

strapdown inertial navigation system(SINS); rotary modulation; inertial frame; initial alignment; gyrocompass

10.13873/J.1000—9787(2017)07—0142—04

2017—05—08

国家自然科学基金重点资助项目(61633008)；国家自然科学基金面上资助项目(61374007)

U 666.1

A

1000—9787(2017)07—0142—04

陈敬萱(1995-)，男，研究方向为计算机与算法。

李 晋(1979-)，女，工学博士，讲师，主要从事模型驱动工程研究工作。