嵌套环式MEMS振动陀螺的静电修调算法*

于得川， 何汉辉， 周 鑫， 肖定邦， 吴学忠

(国防科技大学 机电工程与自动化学院，湖南 长沙 410073)



计算与测试

嵌套环式MEMS振动陀螺的静电修调算法*

于得川， 何汉辉， 周 鑫， 肖定邦， 吴学忠

(国防科技大学 机电工程与自动化学院，湖南 长沙 410073)

对于工作在n=2模态谐振结构，静电修调是一种消除频率裂解、实现模态匹配的常用方法。基于环形谐振子的刚度扰动模型，提出了一种直观而实用的修调算法。通过巧妙地近似，并将嵌套环结构的内置修调电极等效为两簇簇带负刚度的“径向弹簧”，从而将单环谐振结构的理论模型成功应用于多环嵌套结构。最后通过静电修调实验对该算法进行了验证，实现了带误差谐振子的模态匹配。实验结果表明：通过该算法频率裂解从15 Hz左右被修到0.03 Hz左右。

嵌套环式微机电系统振动陀螺； 频率裂解； 频率修调； 模态匹配

0 引 言

嵌套环式微机电系统(MEMS)振动陀螺是新型高性能微机电陀螺之一，它由环形谐振陀螺发展而来，由多个半径递增的同心圆环嵌套而成，环与环之间排布了大量电极[3]。对于工作在n=2模态的谐振结构，当谐振子的质量、密度、刚度等参数分布不均匀，谐振子的二阶振型将出现2个相互间成45°的固有振型轴，沿这2个振型轴的二阶弯曲振型对应的固有频率分别达到极大值和极小值，2个固有频率差称作频率裂解。频率裂解将严重影响陀螺性能，应进行必要的频率修调以减小或消除频率裂解。

通常采用添加[2]或去除质量[3～5]以及静电调刚度[6，7]的方法来进行频率修调。质量修调需要采用复杂的工艺技术，只能在陀螺封装之前进行修调，并且去质量修调会破坏谐振结构。目前，应用最普遍的修调方法是静电调刚度的方法，该方法简单有效，只需建立简单的电路模型，在指定电极施加一定电压即可实现修调。然而，目前大多数的相关研究报道都集中在环形谐振结构的质量修调算法[2～5]，对于多环结构的静电修调算法的研究还比较欠缺。

本文针对多环嵌套结构，基于环形谐振子的刚度扰动模型[8]，通过巧妙的近似以及等效处理，推导出一套直观且实用的静电修调算法，详细阐述了如何充分利用这些排布在环与环之间的电极进行修调，并在实验中得以验证。

1 环形谐振子刚度扰动模型

对于工作在n=2模态的理想无误差环形谐振子而言，假设其谐振频率为ω0。如图1所示，在谐振环上添加N个沿径向方向的弹簧，每个弹簧刚度为Kj，周向位置为φj，j=1,2,…,N。刚度分布不均匀导致了相差45°的2个振型，高频轴角度位置为ψ1，低频轴角度位置为ψ2，且[1]

ψ1=ψ2-π/4

(1)

(2)

图1 加径向弹簧的环形谐振子

较高的频率值ω1与较低的频率值ω2分别为[1]

(3)

式中 α为径向振幅与切向振幅的比值，S0为谐振子在n=2模态的弹性势能。对于一般MEMS技术制造的谐振子，修调前的固有频率与修调后的固有频率相差小于0.3 %，因此，这里可近似认为ω0=ω1=ω2，则式(3)经过简单的转化可得

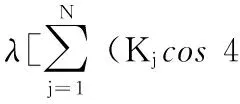
(4)

(5)

则式(4)可以化为

ω1-ω2=σccos4ψ1+σssin4ψ1

(6)

式中 σc，σs命名为“裂解系数”，表示带误差谐振子频率裂解的严重程度，由式(2)可知

tan4ψ1=σs/σc

(7)

综合式(5)～式(7)可得

(8)

即裂解系数可以通过测量频率裂解和振型角度估算得到，实际上裂解系数由式(9)定义。

令Δ=ω1-ω2，根据式(5)～式(8)，频率裂解与刚度分布的关系可简化为复数形式

(9)

以上分析了理想无误差环形谐振子加径向弹簧后的频率裂解情况，而更关心的是与之相反的情况，即带误差谐振子需要在何处添加多大刚度的弹簧,可将频率裂解消除。现考虑一带误差环形谐振子，其裂解因子(σc，σs) 可由式(8)定义。在该谐振子上添加N个径向弹簧进行修调，那么根据式(2)、式(4)和式(8)，修调后的裂解系数可表示为

(10)

以上推导了环形谐振子的刚度修调模型，可将其扩展到如图2所示的多环嵌套结构。

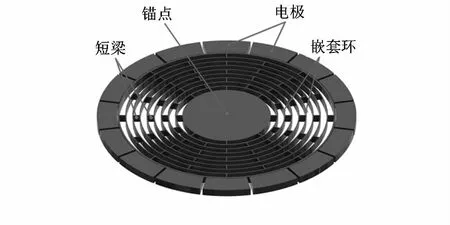
图2 嵌套环陀螺模型 (省略了环与环间的内置电极)

2 嵌套环谐振子静电修调模型

对于多环嵌套结构，可以证明，添加在不同环上的径向弹簧引起的频率裂解仍符合向量叠加的关系[2]，但不同环的敏感系数会有所不同。那么，无误差嵌套环谐振子添加径向弹簧的模型可表示为

(11)

式中 R为嵌套环的总数；λr为第r环的敏感系数；Nr为第r环上弹簧数目。

实际修调中，是通过在电极上加电压来达到改变结构刚度的目的。这里需要对电极向径向弹簧进行等效处理，从而能够套用以上理论模型。等效模型如图3(左图)所示，每个修调电极被均分为若干个小的电极单元，而每个电极单元的内外两侧与其正对谐振结构部分均可近似为如图3(中间图)平行板电容。当谐振子工作在n=2模态，并在电极上加电压V，小电极单元外侧与谐振子重合部分所受的合外力可表示为

(12)

式中 k0为未加电压时的谐振子与电极重合部分的等效刚度；x为电极与谐振结构的间隙；x0为加电压后平衡状态下(未振动)谐振子的位移；Δx谐振子与电极单元重合部分的振动位移；Sout为电极单元与谐振子的重合面积；ε为真空介电常数。加电压后谐振子与电极单元重合部分的等效径向刚度，可通过对式(12)中的Δx求偏微分获得

(13)

表明，加电压后，电极单元外侧所对谐振子位置的径向刚度减小了SoutεV2/(x-Δx)3。同理可证，与此同时电极单元内侧所对谐振子位置的径向刚度减小了SinεV2/(x-Δx)3。因此，加电压后，小电极单元可看成是2个加在与电极相邻的2个环上的径向弹簧，整个电极可等效为2排径向弹簧，如图3 (右图)所示。内侧和外侧等效弹簧的刚度可分别表示为

(14)

式中 t为电极编号，由于Δx≪x，因此，忽略了Δx项。则等效弹簧径向刚度与电压平方成正比。假设每个电极被分成Ne个电极单元，那么根据式(11)，对于理想无误差谐振子，一个加了电压V的电极可引起的频率裂解为

在临床医学中，冠心病主要是指因为患者不正常脂质代谢，在光滑动脉内膜上形成堆积，时间变成体积变大，从而形成白色斑块，称其为动脉硬化，而斑块的大量堆积会造成患者动脉腔逐渐狭窄，导致血液不畅，引发心绞痛，对患者日常生活产生了严重影响[1]。现阶段人们生活习惯与饮食结构发生极大转变，脂肪摄入主要增多，增加了血液粘稠度，从而很容易诱发早发冠心病[2]。本研究中全面分析了诱发早期冠心病的危险因素，并应用Cox回归模型分析探讨危险因素与患者预后的相关性。现报道如下。

(15)

Ne(整个电极被分成的电极单元个数)是一个有限值，因此，每个电极单元的侧面实际上仍为圆弧曲面，本文实际将这些小曲面近似看为平面后才得出式(15)。如果准确计算，可令Ne趋于无穷大，则(15)可化为

(16)

式中 φt为电极t的中心角度位置;Rout和Rin为电极两侧的半径；h为谐振环的高度；θ为电极所对圆心角；γt为一个与谐振子结构参数相关的系数，可通过实验测得，并且与电极所处的径向位置相关，对于处于相同半径的电极，该系数是相同的。那么，与式(16)相应的裂解系数可表示为

(17)

图3 内置修调电极等效模型

现考虑一带误差谐振子，在T个电极上加电压进行修调，那么综合式(9)与式(17)可得修调后的裂解因子为

(18)

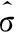
(19)

3 静电修调实验

本文用于修调实验的嵌套环陀螺如图4所示，谐振结构由9个环嵌套而成外侧均布了16个电极S1～S4组用于本实验的驱动和检测。谐振结构最外环半径为4mm，谐振环高度为150μm，为了方便引线，内置电极与外侧检测电极上均镀了一层铝。实验利用了最外2层的16个电极进行修调，修调电极与电源电压连接，如图4所示，则式(19)中，T=16。注意到电极的中心角度的位置满足

φt=(t-1)π/8,t=1,2,…,16

(20)

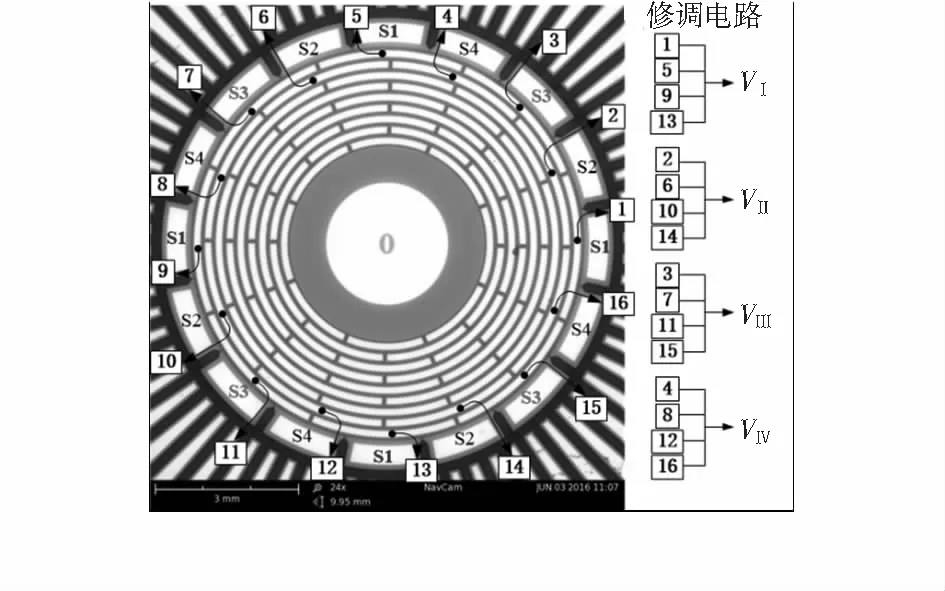
图4 本实验所用陀螺显微图以及驱动检测电极S1～S4,修调电极1～16和修调电路

由于电极位置的特殊性，并且同一半径位置的电极具有相同的系数γt，即

γ1=γ3=…=γ15,γ2=γ4=…=γ16

(21)

为保证修调刚度均匀分布，实验的修调电压也对称施加如图5所示，那么修调方程可进一步简化为

(22)

令式(22)中左边修调后裂解因子为0，即可求解修调电压。一般地

(23)

修调过程首先需要测定频率裂解大小和高频轴方向，进而根据式(10)可求得裂解系数的大小。然而振动轴方向的测定过程比较复杂，而且由于嵌套环陀螺的振型不是标准的椭圆，测定的误差也比较大。因此，本实验只判断了高频轴的范围以及2个频率大小，根据本算法仍然实现了修调。具体过程如下：

1)利用扫频仪进行模态测试，本实验驱动与检测均在相同的4个对称电极上，如图4所示。S1组和S3组电极的频率响应曲线如图5所示，该谐振子的初始频率裂解大小为15.53Hz，并且通过该图可以断定，高频轴在S3电极附近，即S2与S4之间。进一步测试S2组和S4组电极的频率响应曲线，最终可确定高频轴在S2～S3之间，即高频轴在22.5°～45°之间。因此可以确定裂解系数σc<0,σs>0，根据式(23)可知，需要加电压VⅢ和VⅡ进行修调。

图5 S1和S3组电极频率响应曲线

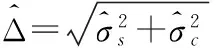
(24)

(25)

图6 频率裂解随电压VⅡ变化曲线

3)保持电压VⅡ=19.80 V，可进行裂解系数σc的修调。由于σc<0，需要加修调电压VⅢ进行修调。此时，根据式(22)和式(25)可知

(26)

接下来加电压VⅢ，从5 V增大到30 V(间隔5 V)，并测试频率裂解的变化，最终结果如图7中数据点所示。同样，曲线为实验数据向理论式(26)的拟合曲线。根据拟合曲线2得出敏感系数γ1的初始估计值为0.003 77 Hz/V2，将γ1的值以及|σc|=14.50 代入式(23)中对应的公式，可算得所需的修调电压VⅢ为31.01 V，将VⅢ调到这个电压值后，测得最终频率裂解如图8所示，约为0.03 Hz。

图7 频率裂解随电压VⅢ的变化曲线

图8 最终修调后S1和S3频率响应曲线

4 结束语

本算法将环形谐振子的修调模型应用到多环嵌套结构，推导出了直观且实用的修调方程。实验中的两条拟合曲线与实验数据非常吻合，并且最终的修调结果也很理想，从而算法的可靠性得到验证。而本算法的应用范围不应局限于嵌套环陀螺或者环形陀螺，简单的仿真结果表明，该算法对半球形以及杯形等对称型陀螺也同样适用。

[1] Challoner A D,Ge H H,Liu J Y.Boeing disc resonator gyro-scope[C]∥Navigat Symp,Monterey,CA,USA:IEEE/ION,2014:504-514.

[2] Schwartz D,Kim D,Stupar P,et al.Modal parameter tuning of an axisymmetric resonator via mass perturbation[J].J Micro-electromech Syst,2015,24(3):545-555.

[3] Rourke A K,McWilliam S,Fox C H J.Multi-mode trimming of imperfect thin rings using masses at pre-selected locations[J].J Sound Vibrat,2002,256(2):319-345.

[4] Rourke A K,McWilliam S,Fox C H J.Multi-mode trimming of imperfect rings[J].J Sound Vibrat,2001,248(4):695-724.

[5] Gallacher B J,Hedley J,Burdess J S,et al.Multimodal tuning of a vibrating ring using laser ablation[J].J Mech Eng Sci,2003,217(5):557-576.

[6] Gallacher B J,Hedley J,Burdess J S,et al.Electrostatic correction of structural imperfections present in a microring gyros-cope[J].J Micro-electro-mech Syst,2005,14(2):221-234.

[7] Ayazi F,Najafi K.A HARPSS polysilicon vibrating ring gyro-scope[J].J Micro-electro-mech Syst,2001,10(2):169-179.

[8] Fox C H J.A simple theory for the analysis and correction of frequency splitting in slightly imperfect rings[J].J Sound Vibrat,1990,142(2):227-243.

[9] 贺 琨,崔红娟,侯占强,等.微机械振动陀螺模态耦合误差分析与激光修形方法研究[J].传感器与微系统,2013,32(3):21-24.

[10] 侯占强,肖定邦,江 平,等.电容式MEMS器件模态频率的电学测试方法研究[J].传感器与微系统,2008,27(5):12-14.

Algorithm for electrostatic tuning of disk resonator MEMS vibration gyroscope*

YU De-chuan, HE Han-hui, ZHOU Xin, XIAO Ding-bang, WU Xue-zhong

(College of Mechatronics Engineering and Automation,National University of Defense Technology,Changsha 410073,China)

For the resonator operating atn=2 modes,electrostatic tuning is a commonly used method to reduce the permanent frequency mismatch.On the basis of the stiffness perturbation model for a ring,an intuitive and utility algorithm is introduced.In this algorithm,each tuning electrode is regarded as two rows of radial springs with negative stiffness,so that the theoretical model of ring resonator is successfully applied in the disk resonator gyroscope.Finally,the algorithm is verified by electrostatic tuning experiment,and matching of the two modes is realized.Results of experiments show that,the frequency split of resonators is decreased to about 0.03 Hz from original about 15 Hz.

disk MEMS resonator gyroscope; frequency split; frequency tuning; matching of modes

10.13873/J.1000—9787(2017)07—0134—04

2016—09—07

国家自然科学基金资助项目(51335011,51575521)

U 666.1

A

1000—9787(2017)07—0134—04

于得川(1990-)，男，硕士研究生，主要研究方向为嵌套环式MEMS振动陀螺的加工工艺与频率修调技术。