一种改进的LLR BP译码算法研究*

高 杰, 龙 华, 邵玉斌, 张 强

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)



一种改进的LLR BP译码算法研究*

高 杰, 龙 华, 邵玉斌, 张 强

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

运用LLR BP经典算法对低密度奇偶校验 (LDPC) 码译码时，由于译码时迭代次数过多和每次循环时校验节点的计算复杂度过高，导致译码复杂度非常高。提出了一种改进型LLR BP译码算法，采用泰勒级数将LLR BP算法中复杂度高的雅克比修正项进行分段线性近似。仿真表明:该算法在译码性能损失不大的情况下可大幅降低 LDPC 码的译码复杂度。

LLR BP算法； 低密度奇偶校验码； 泰勒级数； 分段线性近似

0 引 言

低密度奇偶校验(low density parity check,LDPC)码具有结构简单、在高斯信道下接近香农限和超越主流Turbo码的译码性能[1]，已成为当今通信领域的研究热点。

影响码的编码性能和发展(尤其是长码)最重要的一个因素是译码算法。当今国内外学者对降低LDPC码译码算法复杂度和促进LDPC码的发展作出了大量贡献，相继提出了一些简化的译码算法[2,3]。LDPC码的译码算法主要分为基于软判决的置信迭代译码和基于硬判决的比特翻转译码两大类。基于软判决译码，码性能可逼近香农限，译码性能较好，但实现复杂度高;基于硬判决译码，译码性能较差但实现复杂度低[4～6]。LLR BP是基于软判决的置信迭代译码算法，译码性能好，但其运算复杂限制了在实际中的应用，因此，本文提出了一种改进的LLR BP译码算法。

1 LLR BP译码算法

BP译码的核心思想是在变量节点和校验节点之间对信道接收的信息反复进行迭代运算译码，其涉及大量的乘法和加法运算。LLR BP 译码算法是将BP译码算法中的运算域变换到对数域中，将大量的乘法变换成加法运算，大大减少了运算量[7,8]。

简单起见，定义如下参数:编码后的信息码元c=(c1,c2,…,cn)；接收的码元y=(y1,y2,…,yn)；变量节点i传递给校验节点j的信息qij(b),b=0,1；变量节点i接收到校验节点j传递的信息为rji(b),b=0,1；与变量节点i相连的校验节点j的集合C(j)；与校验节点j相连的变量节点i的集合R(j)。

LLR BP算法的译码基本步骤如下[9]:

1)信道初始化

信道传递给变量节点的信息概率的似然比为

(1)

2)迭代处理过程

双曲正切函数

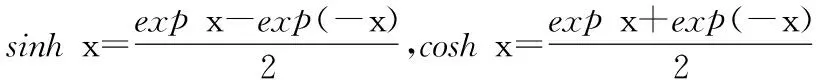
=p0-p1=1-2p1

(2)

校验节点消息处理

(3)

式中 ∂i′j=sign(L(Pi)),βi′j=|L(Pi)|

变量节点消息处理

(4)

译码判决,即变量节点利用收集到的所有信息进行判决

(5)

3)停止

LLR BP 算法充分利用了信息节点和校验节点性质以及接收序列的所有信息，从而可以得到逼近香农极限的译码性能。但由于译码时迭代次数过多和每次循环时校验节点的计算复杂度高，导致译码复杂。

2 LLR BP译码算法优化

提出采用泰勒级数对LLR BP 算法中运算复杂的雅克比修正项进行分段线性近似，对校验节点进行更新。根据文献[10]中的方法对式(3)中tanh(x)进行变换处理得到

L(M⊕N)=sign(L(M))sign(L(N))min(|L(M)|, |L(N)|)+log(1+exp(-|L(M)+L(N)|))- log(1+exp(-|L(M)-L(N)|))

(6)

校验节点传递的外部消息

(7)

式中M,N为独立的二进制随机变量；L(M),L(N)为M和N的似然比；fi,bi分别为一组辅助的二进制随机变量；dc为LDPC码的检验度；⊕为逻辑模运算。

分别对fi,bi利用传送的码元x={x1,x2,…,xn}和式(6)进行递归操作，得到L(fi)和L(bi)；通过(xn1⊕xn2⊕…⊕xnd)=0得到xni=(fi-1⊕bi+1)，i∈{2,3,…，dc-1}；利用前后向的递归运算来完成校验节点更新。

本文提出的线性分段近似算法:用函数I(x)=log(1+e-|x|)表示式(6)的修正项，以函数I(x)的切点x0对曲线I(x)在泰勒级数近似的基础上进行线性分段近似，分段步长为0.85，具体如表1所示。

表1 曲线I(x)=log(1+e-|x|)分段近似函数

文献[11]使用泰勒级数中的修正项进行修正，该文献中泰勒级数近似于原曲线的最大误差为30.586 9，而本文提出的线性分段近似于原曲线的最大误差只有0.128 1，有效降低了译码时产生的误码率。

提出的线性分段近似译码算法与经典的LLR BP算法相比，将曲线近似分段成直线，避免了非线性的对数运算，降低了运算复杂度，其译码性能与LLR BP 译码算法基本一致，且更利于实际应用中的操作。

3 性能仿真

使用Matlab进行仿真验证。仿真中信道采用AWGN信道，调制方式为BPSK，LDPC码元分别为(5 00,3,6)和(5000,3,6)，码率为1/2，迭代次数分别设为40次和80次。仿真结果如图1所示。由图1、图2可知，无论是在长码还是短码的情况下，在低信噪比小于1.0 dB条件下，LLR BP和优化的LLR BP算法译码性能几乎一样，当误码比特率为10-2时本文提出的优化算法要优于经典LLR BP算法。

图1 2种迭代次数下(5 000,3,6)LDPC译码性能

4 结束语

与LLR BP 译码算法相比，采用泰勒级数对LLR BP 算法中复杂度高的雅克必修正项进行分段线性近似，避免了查表操作和复杂的非线性对数函数的计算。在没有改变译码性能的前提下，大大降低了译码运算复杂度。

[1] Wang Kaiyao，Xiao Yang，Kim K.Construction of time frequency codes based on protograph LDPC codes in OFDM communication systems[J].Journal of Systems Engineering and Electronics，2012，23 (3):335-341.

[2] 田 进，王毓玲，马正新.一种卫星突发通信中抗相位模糊LDPC译码算法[J].传感器与微系统，2012，31(12):140-142.

[3] 陈允锋，董继刚.LDPC码在基于FH-FSK的AUV水声通信系统中的应用[J].传感器与微系统，2015，34(12):156-160.

[4] 沈雪梅.下一代无线局域网中LDPC译码算法研究[J].科技通报,2013，29(2):127-129.

[5] 乔晓峰，刘跃敏，宁永海.RS码与QC-LDPC码的级联码在浅海信道中的性能研究[J].电子技术应用，2012，38(5):122-124.

[6] 杨志良，李晋华.LDPC编码在无线传感器网络中的应用[J].传感器与微系统，2013，32(10):139-141.

[7] 袁东风，张海刚.LDPC码理论与应用[J].北京:人民邮电出版社，2008.

[8] 卢建波.硬判决LDPC 译码算法在卫星导航中的应用[J]. 无线电工程，2012，42(9):38-40,64

[9] Kschischangf R J，Loeligerh A.Factor graphs and the sum-product algorithm[J].IEEE Transaction on Information Theory，2009，47(2):498-519 .

[10] 胡树楷 ，王新梅.一种简化的GF(q)-LDPC码译码算法[J].西安电子科技大学学报 ，2011，38(2):8-12.

[11] Chen Jinghu，Dholakia A，Eleftheriou E，et al.Reduced-complexity decoding of LDPC codes[J].IEEE Transaction on Communications，2005，53(8):1288-1299.

Research on improved LLR BP decoding algorithm*

GAO Jie, LONG Hua, SHAO Yu-bin, ZHANG Qiang

(Faculty of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650500，China)

When classical log likelihood rate belief propagation(LLR BP)is applied to decode low density parity check(LDPC) code, it becomes very complex because of excessive number of iterations and high computation check complexity of parity check nodes at each iteration. To solve this problem, a modified LLR BP decoding algorithm is proposed, which approximating the highly complex Jacobi correction term in LLR BP algorithm segmentally and linearly by Taylor series.Simulation shows that it becomes less complex than LDPC decoding in case of not too much loss of decoding performance.

log likelihood rate belief propagation(LLR BP)algorithm;low density parity check(LDPC) code;Taylor series;piece wise linear approximation

10.13873/J.1000—9787(2017)07—0070—03

2016—06—21

2014云南省科技厅基金资助项目(2014RA051);2013云南省科技厅基金资助项目(2013FZ010)

TP 212

A

1000—9787(2017)07—0070—03

高 杰(1991-)，男，硕士研究生，主要研究方向为信息处理，E—mail:gaojie_swfu@163.com。

龙 华(1963-)，女，通讯作者，教授，硕士生导师，主要从事信息处理方向研究工作，E—mail:1228627124@qq.com。