帐篷混沌序列稀疏测量矩阵构造*

胡行华， 史明洁

(辽宁工程技术大学 理学院，辽宁 阜新 123000)



帐篷混沌序列稀疏测量矩阵构造*

胡行华， 史明洁

(辽宁工程技术大学 理学院，辽宁 阜新 123000)

测量矩阵的构造是压缩感知(CS)中重要的研究内容之一。利用混沌系统伪随机性、遍历性的特点，提出了一种基于帐篷混沌序列构造确定性稀疏随机矩阵的方法。对混沌系统生成的确定性序列进行了间隔采样，采样后的序列满足统计独立性，然后通过符号函数映射，生成了具有稀疏性质的伪随机序列，进而构造出混沌稀疏测量矩阵。仿真实验表明：该方法构造出的混沌稀疏测量矩阵与高斯随机矩阵、稀疏随机矩阵及Bernoulli随机矩阵相比，具有类似的重构性能。混沌系统参数与初值固定时，构造的混沌稀疏测量矩阵是确定的，计算复杂度小且硬件上容易实现。

压缩感知； 混沌系统； 测量矩阵； 稀疏矩阵

0 引 言

传统信号采样理论中，信号的采样速率必须达到信号最高频率的2倍或2倍以上才能够精确重构原始信号。近年来，Candes E，Donoho D和 Tao T提出了一种新的信号采样理论—压缩感知(compressed sensing，CS)[1,2]。CS理论突破了奈奎斯特采样定理对采样频率的限制，使数据的压缩与采样同时进行，为高速数据的采集、存储、传输和处理等带来极大便利，具有良好的应用前景。目前，CS理论应用的热点领域有图像处理[3]、语音信号处理[4]和无线传感器网络[5,6]等。

CS理论主要包括信号的稀疏表示、测量矩阵的设计以及信号重构三方面内容。其中，测量矩阵的设计在信号采集和重构环节起到至关重要的作用。CS的测量矩阵可分为稠密矩阵和稀疏矩阵。目前，稠密矩阵在理论上有很好的特性，但这类矩阵密度高、存储空间大、计算复杂度高且不易硬件实现，如高斯随机矩阵等。因此,在大多数应用中，更希望测量矩阵是稀疏的。张波等人[7]证明了当测量值个数满足特定条件时，稀疏随机矩阵以接近于1的概率满足有限等距性质。孙晶明等人对稀疏随机矩阵的观测次数下界进行研究，推导了观测次数应满足的下界条件[8]，提出了CS块稀疏循环矩阵，但所提的矩阵元素为高斯随机变量，限制其硬件友好性。Berinde R等人[9]采用二值稀疏随机矩阵作为观测矩阵，并在通用的重建算法下与高斯随机矩阵的重建性能相当。Li Shuxing等人[10]提出了利用有限几何构造了确定性稀疏测量矩阵的方法，但是该方法不能构造大小任意的确定性测量矩阵，具有一定的局限性。

本文将帐篷混沌系统所生成的混沌序列用于构造CS中确定性稀疏测量矩阵。构造的混沌稀疏测量矩阵克服了随机测量矩阵的不确定性及硬件上难以实现的缺陷。混沌稀疏测量矩阵只需要存储和传输少量混沌系统参数，并对信号重构时不需要大量重复实验，减少了存储空间，节约了资源。

1 CS理论

对离散信号x∈RN，如果x本身是可压缩的或在一组N×N维正交基Ψ上展开为

(1)

式中x和α均为N×1维向量。当系数向量α中至多有k(k≪N)个非零值或k个比较重要的参数时，x被称为k稀疏信号。实际中，信号往往不是稀疏的，需要经过式(1)的变换，此变换称为信号的稀疏表示。常用的稀疏基有小波基、正余弦基及Curvelet基等。

将信号x投影到一组矩阵Φ∈RM×N(其中M≪N)上，得到关于信号x的观测值y(y∈RM)，即

y=Φx=ΦΨα=Θα

(2)

式中Φ为测量矩阵；Ψ为稀疏基；Θ=ΦΨ为传感矩阵。

为了保证准确重构出信号x，传感矩阵Θ必须满足约束等距性质[1](restricted isometry property,RIP)

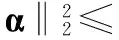
(3)

式中 δk被称为约束等距常数。依据式(3)判断传感矩阵Θ是否满足RIP条件比较困难，因此，Baraniuk提出其等价条件，即观测矩阵Φ和正交稀疏基Ψ不相关条件。常用的观测矩阵有高斯随机矩阵、贝努利随机矩阵、稀疏随机矩阵、托普利兹和循环矩阵等。

在满足以上条件下，通过式(2)，可以利用少量的测量值y通过优化算法计算出信号x的稀疏表示α，最后通过逆变换恢复信号x。具体优化算法可以利用l0范数优化方法求解α的精确解或者一个逼近，即

(4)

由于式(4)的优化问题是NP-Hard问题，所以，在一定条件下可用l1范数代替l0范数求解，即

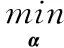
(5)

针对信号α的重构，CS理论中已经有一系列近似求最优解的重建算法，主要可以分为以下三大类:第一类是基于l0范数最小化的贪婪迭代匹配追踪系列算法;第二类是基于l1范数最小化的松弛算法；第三类是以贝叶斯统计为代表的非凸优化算法。

2 混沌稀疏测量矩阵的构造

2.1 一维混沌系统

混沌是非线性系统所独有且广泛存在的一种非周期运动形式，由于混沌系统产生的序列具有确定性和随机性的统一、有界性以及遍历性等良好的伪随机性质，所以，在非线性控制、信号处理、保密通信等领域有着广泛应用[11，12]。

帐篷映射是一种应用相当广泛的离散混沌系统，其映射方程的数学表达式为

xn+1=α-(1+α)|xn|,n=1,2,…

(6)

式中 α∈(0,1)，本文令α=0.999，迭代初值x0=0.01。与其他同类型混沌映射相比，如Logistic映射、立方映射和无限折叠映射，从熵性质可得出帐篷映射比其他三种混沌映射稳定性都要好，同时，从仿真图也可看出，其遍历的均匀性是不一样的，以帐篷映射最好，见图1。

图1 不同类型混沌序列分布

其中，横坐标表示范围(均分区间)，纵坐标表示次数(n=10 000)。如Logistic映射产生的混沌序列落在 0 %～10 %,即[0,0.1]内的点有2 000余个，以此类推。

2.2 混沌稀疏测量矩阵构造算法

本文利用帐篷映射生成的确定性的混沌序列构造混沌稀疏测量矩阵，具体步骤如下：

1)通过帐篷映射产生一个M×N×d的确定性的混沌序列为

{an|n=0,1,…,M×N×d,an∈(-1，1)}

式中d为采样间隔，取d=15。

2)对序列an进行间隔采样，生成新的序列

{bn|bn=an×d,n=0,1,…,M×N-1}

采样后的序列bn中元素是近似相互独立的并且满足同分布[13]。

3)结合稀疏随机矩阵性质，取稀疏率为0.2，生成序列元素均为正数，将序列bn经过式(7)符号函数映射成序列xn，即

(7)

4)按行的方式将xn转换生成一个大小为M×N的观测矩阵Φ，如式(8)，并经过一个变换L对Φ进行标准化

(8)

如此，测量矩阵构造完成，测量值y可通过式(2)获得。

3 实验分析

为验证本文关于混沌稀疏测量矩阵构造算法的可行性及混沌稀疏测量矩阵的有效性，实验分别采用高斯随机测量矩阵、Bernoulli随机测量矩阵、稀疏随机矩阵及构造的混沌稀疏测量矩阵进行仿真，并对结果进行对比和分析。

3.1 一维信号仿真实验

本文为减小实验难度，减少因素干扰，选取长度N=256的绝对稀疏0～1随机信号，利用子空间追踪算法(subspace pursuit，SP)对随机信号进行重构。实验假设信号重构残差‖x-xrec‖2小于0.001时信号重构成功，其中,x为原始信号，xrec为重构信号。

CS理论中，信号的稀疏度和测量次数都会影响信号重构效果。因此，实验首先假定测量次数固定，分析仅改变随机信号的稀疏度时对信号重构成功概率的影响；然后假定随机信号稀疏度固定，分析仅改变测量次数时对信号重构成功概率的影响。除本文构造的混沌稀疏测量矩阵外，为减小实验中随机测量矩阵的不确定性影响，其余测量矩阵均进行200次独立模拟实验取平均值，结果如图2、图3所示。

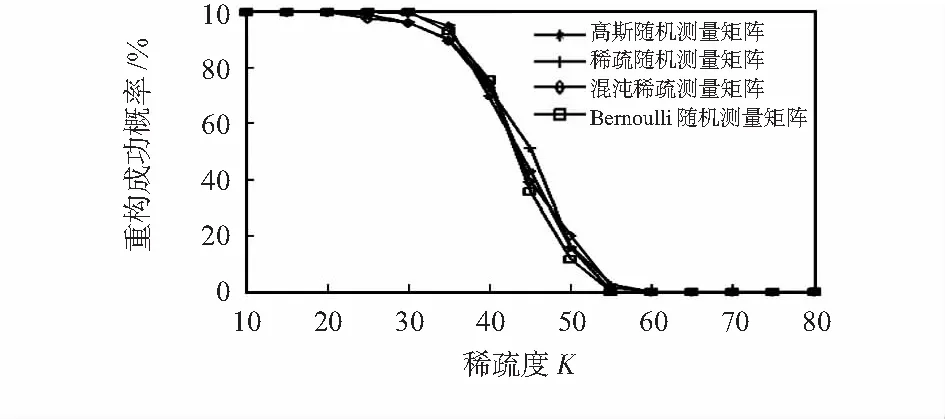
图2 N=256，M=128时，不同测量矩阵重构效果随稀疏度K变化

图3 N=256，K=30时，不同测量矩阵重构效果随测量次数M变化

图2表明：当随机信号的稀疏度K≤30时，几种测量矩阵都能以高概率重构出原始信号；当稀疏度K≥55时，都不能对原始信号进行重建。图3表明：当测量次数K≥135时，几种测量矩阵都能以高概率重构出原始信号；当测量次数K≤85时，都不能对原始信号进行重建。从图2和图3可知：在相同的条件下，本文构造的混沌稀疏测量矩阵和其他几种测量矩阵具有类似的性能，都能实现对一维信号的重构。

3.2 二维图像重构实验

本文采用大小为 的Lena图像，稀疏基采用离散余弦变换基(DCT),重构算法采用平滑l0范数(smoothedl0norm，SL0)算法。

实验在不同采样率(M/N)下比较不同观测矩阵对重构效果的影响，同一维信号实验，本文进行100独立实验取平均值，并采用峰值信噪比(peak signal to noise ratio， PSNR)作为评价标准，定义为

式中 I为原图像，R为重构图像。MAXI为图像点颜色的最大数值(如果每个采样点用 8 位表示，那么就是255)。PSNR的值越大，表示信号重建的精确度越高，则对应的混沌观测矩阵性能也就越好。实验结果如图4。

图4 图像在不同测量矩阵下的峰值信噪比随采样率变化

为了直观展示，在采样率M/N=0.5时，重构效果如图5所示。

图5 Lena图像重构效果对比

可以看到，在相同采样率(M/N)的情况下，本文构造的混沌稀疏随机矩阵与高斯随机测量矩阵、稀疏随机矩阵以及Bernoulli随机测量矩阵有类似的重构效果。

4 结 论

本文将帐篷混沌系统生成的确定性混沌序列用于构造混沌稀疏测量矩阵。对一维信号和二维图像进行信号重构对比仿真。实验结果表明：本文构造出的混沌稀疏测量矩阵与高斯随机矩阵、稀疏随机矩阵及混沌矩阵相比，具有类似的重构性能。由于本文构造的测量矩阵在采用的混沌系统的参数和初值确定时是固定的，克服了随机测量矩阵的不确定性，硬件上难以实现的缺点。并且由于只需要存储混沌系统参数和稀疏矩阵的性质，可以节省存储空间和传输带宽，硬件易于实现，基于混沌系统构造的测量矩阵是确定的，容易在硬件上实现，而且矩阵稀疏的性质，对减少存储空间有很大帮助，具有一定的实用意义。

[1] Candes E,Romberg J,Tao A T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[2] Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[3] 任越美,张艳宁,李 映.压缩感知及其图像处理应用研究进展与展望[J].自动化学报,2014,40(8):1563-1575.

[4] 苗曙光,李淮江,刘晓文.基于压缩感知和WSNs的井下应急语音通信系统设计[J].传感器与微系统,2015,34(12):108-114.

[5] 顾逸宸,黄 如.基于压缩感知的链型无线传感器网络节能数据收集[J].传感器与微系统,2015,34(11):69-74.

[6] 李 鹏,王建新.UWSNs中基于压缩感知的移动数据收集方案[J].传感器与微系统,2016,35(5):49-54.

[7] 张 波,刘郁林,王 开,等.稀疏随机矩阵有限等距性质分析[J].电子与信息学报,2014,36(1):169-174.

[8] 孙晶明,王 殊,董 燕,等.稀疏随机矩阵的观测次数下界[J].信号处理,2012,28(6):879-885.

[9] Berinde R,Indyk P.Sparse recovery using sparse random matrices[R].Boston:MIT-CSAIL Technical Report， 2008．

[10] Li Shuxing，Ge Gennian.Deterministic construction sparse sensing matrices via finite geometry[J].IEEE Transactions on Information Theory,2014,62(11):2850-2859．

[11] 刘叙含,申晓红,姚海洋,等.基于帐篷混沌观测矩阵的图像压缩感知[J].传感器与微系统,2014,33(9):26-31.

[12] 邵克勇，徐 向，陈伯全.超混沌系统的滑膜同步控制[J].自动化技术与应用，2016,35(4)：1-5.

[13] lei Y,Barbot J P,Gang Z.Compressive sensing with chaotic sequence[J].IEEE Signal Processing Letters,2010,17(8):731-734.

史明洁(1991-),通讯作者，E—mail:932559492@qq.com。

Construction of sparse measurement matrix via tent chaotic sequence*

HU Xing-hua， SHI Ming-jie

(College of Science，Liaoning Technical University，Fuxin 123000，China)

Construction of measurement matrix is one of the important research content in compressed sensing(CS).Using characteristic of pseudo randomness,ergodicity of chaotic systems,propose a method for construction of the sparse measurement matrix based on tent chaotic sequence.The method for deterministic chaotic sequence generated by the system will be interval sampling,so that the sampled sequence meet statistical independence,by symbol function mapping generate pseudo-random sequence having sparsity,thereby construct measurement matrix of chaotic sparse.Simulation experiments results show that compared with Gaussian random matrices,sparse random matrix and Bernoulli random matrix, this proposed matrix has a similar reconstruction performance.The proposed measurement matrix is deterministic when parameter of chaotic system and initial value are fixed，its computation complexity is small and it is easy to be realized by hardware.

compressed sensing(CS)； chaotic system； measurement matrix； sparse matrix

10.13873/J.1000—9787(2017)07—0050—03

2016—08—16

国家自然科学基金青年科学基金资助项目(11401284)；教育部高校博士学科科研基金联合资助项目(20132121110009)；辽宁省教育厅基金资助项目(L2015108)

TN 911.7

A

1000—9787(2017)07—0050—03

胡行华(1978-)，男，副教授，硕士生导师,从事混沌动力系统分析与预测研究工作。