局部遮阴下光伏系统MPPT研究与优化

吴 琨， 王 磊， 王秋实， 陈 东

(1.辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105;2.浙江艾罗电源有限公司，浙江 杭州 310000)



局部遮阴下光伏系统MPPT研究与优化

吴 琨1， 王 磊2， 王秋实1， 陈 东1

(1.辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105;2.浙江艾罗电源有限公司，浙江 杭州 310000)

为了解决光伏发电系统中，光伏电池在环境中被树叶、建筑物、云层等遮挡造成局部阴影，导致光伏电池出现运行不稳定和输出功率降低的问题,提出了一种基于改进自适应动态惯性权重并引入粒子寻优目标适应度评判系数的优化粒子群算法(GPPSO)。将GPPSO应用于复杂自然环境条件下的最大功率点跟踪(MPPT)，结果表明：双重优化后的算法有效提高了局部精确搜索和寻优空间全局收敛能力，在目标函数最优求解过程中，精度和收敛速度都明显提高，较快地适应环境遮阴变化，能够在复杂的自然环境中准确地对光伏发电系统最大功率点进行跟踪，提高光伏系统发电效率。

光伏系统； 遮阴条件； 改进粒子群优化算法； 最大功率点跟踪效率

0 引 言

作为一种新兴的清洁、可再生绿色能源，太阳能已经在世界范围内受到高度重视并取得了长足进展，基于太阳能的光伏发电有望成为缓解全球性能源危机和日益严重的环境问题的关键技术之一[1]。光伏(photo voltaic,PV)发电系统中，由于光伏阵列长期工作在户外，光伏电池在工作中被树叶、建筑物、云层等障碍物遮挡而局部产生阴影，导致光伏电池输出特性受到巨大影响，光伏电池P-V特性曲线会出现多个局部峰值点，造成系统最大功率点跟踪(maximum power point tracking,MPPT)困难[2]。

如何更加高效地利用太阳能资源是当今光伏发电行业面临的刻不容缓的一大难题。目前，国内外很多学者致力于光伏阵列的MPPT问题研究，积累了丰富而宝贵的经验，大多数MPPT方案适用于理想光照条件下，应用于固定局部阴影条件下。针对复杂自然遮阴条件，光伏阵列输出功率多峰值导致最大功率跟踪难，低效率的难题，使用传统MPPT研究方法鲜有取得突破性的进展[3～5]。本文充分模拟研究了由多个局部自然阴影动态变化组成的复杂阴影遮盖条件下光伏电池和光伏阵列输出特性，在此基础上，提出了一种基于改进自适应惯性权重系数,同时,引入了寻优目标适应值评判系数的优化粒子群(GPPSO)算法，将其应用于复杂自然遮阴条件下光伏阵列的MPPT。通过建立复杂自然遮阴条件下的光伏阵列数学模型，得到更加精准的光伏电池输出特性函数，设计了基于GPPSO的光伏发电系统MPPT系统，最后制作了实验样机，搭建实验平台，进行了实验和分析研究，结果表明：该方法使整个MPPT控制系统的动态和稳态性能得到提高，避免了局部最优解的情况，有效提高光伏列阵的输出和太阳能利用效率。

1 复杂遮阴环境下光伏阵列建模分析

1.1 单体光伏电池数学模型

考虑到复杂自然遮阴环境导致光伏发电系统MPPT误差，要提高光伏阵列工作效率，首先要研究局部阴影对光伏阵列输出特性的影响[6]。研究所采用的单体光伏电池，其规格参数为：最大输出功率Pm=100 W,开路电压Uoc=40 V，短路电流Isc=3 A，最大功率点电压Um=35 V，最大功率点电流Im=2.8 A，选取参考温度为25 ℃,参考光照为1 000 W/m2。通过简化光伏电池的内部电路结构及其外部输出特性，得到单体光伏电池等效电路如图1所示。

图1 单体光伏电池的等效电路模型

图中Rl为光伏电池的输出负载，Ul为光伏电池输出电压，Il为电池输出电流，Rsx和Rsh分别为电池内部串联等效电阻和旁漏电阻，其中Rsh的阻值一般较大，多为几千欧，Rsx值一般为1 Ω左右，可忽略不计，Ivd为流过等效二极管的电流称为暗饱和电流，Iph为光生电流。

分析上述光伏电池等效电路模型和电路的伏安特性，可以得到单体光伏电池的特性方程如式(1)～式(5)所示

Il=Iph-Ivd-Ish

(1)

Iph=[Iscr+K1(T-25)]λ/100

(2)

(3)

(4)

(5)

式中Io为光伏电池暗饱和电流；q为电子的电荷量；K为玻尔兹曼常数；T为光伏电池的温度；Tr为参考温度；Ido为参考温度下暗饱合电流；Eg为半导体材料的禁带宽度；A为理想因子；Iscr为标准测试条件下光伏电池的短路电流；K1为短路电流的温度系数；λ为日照强度[7,8]。

综上分析，可得光伏电池的输出功率表达式

(6)

式中CT为温度系数，A/K。

1.2 光伏阵列多峰数学模型分析

分析上述光伏电池的输出功率表达式，可以得出，光伏电池的输出特性与光照强度以及环境温度有关，并且呈非线性关系。受单体光伏电池输出功率小的限制，实际的大规模光伏系统中，通常会将多个单体光伏电池进行串、并联组合，以组成大规模光伏阵列来满足负载大输出功率的需求。串并联后,考虑复杂遮阴条件的光伏阵列多峰模型数学模型为

(7)

Uarray=maxUl

(8)

式中np,ns分别为光伏电池的并联个数和串联个数;Iarray,Uarray分别为光伏阵列的输出电流和输出电压;Ul,Il分别为单个串,并联光伏电池的输出电压,输出电流。

1.3 光伏阵列特性曲线分析

当太阳光照均匀分布的情况下，光伏阵列的P-U特性曲线只有一个峰值即最大功率值点，图2、图3分别为不同光照条件和不同温度条件下光伏电池的P-U特性曲线。当太阳能光伏电池板受到环境中障碍物遮盖光伏电池被时，其功率特性曲线会出现多个极值的情况，因此,导致MPPT时会遇到多个局部最大值，如图4曲线所示，此时求出的最大功率可能并非实际的最大功率点，从而出现较大误差。

图2 不同光照条件下光伏电池的P-U特性曲线

图3 不同温度条件下光伏电池的P-U特性曲线

图4 光伏阵列复杂遮阴条件下多峰值P-U特性曲线

2 基于GPPSO算法光伏系统抗干扰的MPPT实现

2.1 粒子群优化算法原理

粒子群优化(particle swarm optimization,PSO)算法是一种简单而有效的启发式算法， 假设每个寻优问题的解都是搜索空间的一个粒子，第i个粒子在n维空间里的坐标位置和速度可表示为[9,10]

Xi(t)=(xi1,xi2,…,xin)

(9)

Vi(t)=(vi1,vi2,…,vin)

(10)

在对n维向量空间上第i个粒子k+1次迭代速度和位置的更新可以由以下寻优化推导方程式(11)～式(12)描述

(11)

(12)

在最大化目标寻优问题中，定义目标函数值f(X)越大，其适应值越优秀，两个极值定义如下式所示

(13)

f(Pg)=max[f(Pi)],1≤i≤n

(14)

式中 f为目标函数，用来存储当前寻优最好的位置，应该取最大化。

2.2 GPPSO算法

以PSO算法为基础，提出改进种群粒子数目、优化自适应惯性权重系数，同时，引入目标适应度函数权重系数比较以提高收敛速度和精度的优化粒子群算法，即GPPSO。

1)优化自适应惯性权重系数

算法的惯性系数表达式调整为

(15)

式中f为当前粒子适应值;fave为所有粒子的平均适应值;fmin为全局粒子中最小适应值。经过改进自适应惯性权重系数后，保证了算法全局寻优和局部搜索的动态平衡，兼顾提高了搜素精度和优化收敛速度。

2)修正全局粒子个数

(16)

迭代更新的判别操作过程如式(17)所示

(17)

式中 a∈[0,1]，本文中，根据光伏发电系统的实际要求，取a=0.05。

2.3 基于GPPSO算法在光伏发电MPPT中应用

GPPSO算法在优化求解复杂多变量函数和多峰值系统寻优时，具有收敛速度快、动态特性好、搜索精度高、不易陷入局部最优值的优点，因此适合自然环境导致光伏电池局部遮阴下最大功率点多峰值模型寻优问题。

将光伏阵列的输出电压Uout定义为粒子寻优空间的位置变量Xi，总输出功率Pout定义为粒子群寻优化目标函数f，通过传感器对光伏电池输出电流、输出电压值进行实时采样，然后计算出光伏电池的瞬时总输出功率Pout，当粒子的目标函数值优于平均目标值，则减小该粒子的惯性权重系数，反之则增大该粒子的惯性权重，使得粒子在寻址空间具有更好的搜索视野[11～13]。其次,在运用该算法实施光伏发电MPPT时，可以充分发挥算法中引入的目标适应值判定系数的优势，避免实时计算采样时刻的最大功率带来剧烈的输出功率振荡。具体操作为，通过计算相邻两个采样时刻的功率变化率 (如式(18)所示)作为PSO算法目标函数适应值判定系数，结合上文分析，当K≤0.05时，PSO算法停止迭代,以此提高收敛速度，避免冗余迭代。此时定义的目标函数(即总输出功率表最大值Pout)等同于上文中目标适应值评判系数

(18)

式中 Pi为当前采样时刻光伏阵列瞬时输出功率。

以上文的单体光伏电池为例，此时系统MPPT算法的适应值函数和全局寻优的目标函数Pg(即光伏电池输出总功率Pout)如式(19)～式(20)所示

(19)

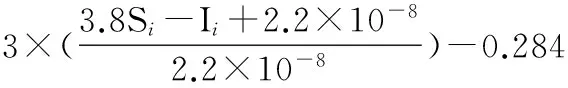
(20)

式中 Ii,Si及Ti分别为单个光伏电池的输出电流、光照强度、参考温度；Pout(Ii,Si,Ti)为光伏电池的输出功率，i=1,2,3，…，n；本文设计使用4个光伏电池，因此，取i=4，设定计算温度为25 ℃，通过调用适应度函数可以得到输出功率值的大小，即目标函数，调用次数由目标函数的适应值判定系数K确定，K为变量，当目标函数适应值判定系数K达到迭代终止条件，停止迭代并进入局部寻址空间进行更精确寻优化操作。

3 光伏系统抗干扰MPPT模拟实验与分析

为了验证本文提出的基于改进自适应惯性权重，同时引入目标函数适应值评判系数双重优化的PSO算法在实际光伏发电系统中的有效性和可行性，设计制作了一台150W具有MPPT控制模块的光伏发电DC—DC变化器样机，并构建了基于DSP数字控制具有MPPT功能的光伏发电系统(系统结构参见图5)实验平台。在实验平台上进行了实验，采用3台可编程直流电源和1块光伏电池模拟光伏发电系统实际工作中，自然环境下导致光伏电池局部阴影和固定局部阴影两种情况下，光伏阵列输出功率多峰值和不平衡现象。

具体操作采用恒压变流模式，在保持直流电源输出电压20V不变的情况下，通过动态调节直流稳压电源，使输出电流范围从5A到2A再到5A连续运行，分别采用传统PSO算法和本文提出的GPPSO算法下变换器的输出波形如图6所示。

图5 基于DSP控制具有MPPT功能模块的光伏发电系统

图6 基于两种PSO算法的光伏列阵输出功率波形

分析图6实验波形可知，与传统PSO控制算法相比，采用本文提出的GPPSO的算法，系统动态响应速度更快，稳态精度更好，系统具有更好的跟踪性能。

4 结 论

本文分析了自然环境导致光伏电池局部遮阴条件下太阳能发电系统出现的运行不稳定和输出功率多峰值现象，分析了传统PSO算法只能适应固定局部阴影时MPPT，而不能应用在复杂的自然环境导致的遮阴条件的缺点，提出了一种GPPSO算法。本文将提出的基于GPPSO算法抗自然环境下导致的复杂遮阴条件光伏阵列MPPT系统，与传统PSO算法的进行对比实验和仿真。实验结果表明：该算法兼顾提高了系统的全局寻优求解和局部精确搜索能力，改进后的算法能够较快适应环境变化，避免冗余迭代、系统的“早熟”和局部最优问题，较大程度上起到了提高光伏列阵的工作效率，可以推广应用在大规模的光伏发电系统。

[1] 李鹏梅,臧传治，李鹤鹏，等.基于光伏预测的微电网能源随机优化调度[J].传感器与微系统，2015，34(2):61-64.

[2] 蔡纪鹤,李 蓓，廉春原,等.光伏发电系统M PPT控制及其实验研究[[J].电源技术，2016,40(5)：1049-1051.

[3] 王 军，张 静，蒋小川.生态物联网节点的风光混合量变换系统设计能[J].传感器与微系统，2014，33(10):54-57.

[4] 李源源，黄守道，陈小青，等.基于无线传感器网络的光伏系统MPPT应用研究[J].传感器与微系统，2012，31(10):64-67.

[5] 程 泽，徐 勇，董梦男.一种新的光伏阵列故障诊断与定位方法[J].传感器与微系统，2013，32(7):26-28.

[6] 胡义华，陈 昊，徐瑞东，等.光伏电池板在阴影影响下输出特性[J].电工技术学报，2011,26(1)：123-128.

[7] 聂晓华，赖家俊.局部阴影下光伏阵列全局最大功率点跟踪控制方法综述[J].电网技术，2014,38(12)：3279-3285.

[8] Boztepe M,Guinjoan F,Velasco Quesada G,et a1.Global MPPT scheme for photovoltaic string inverters based on restricted voltage window search algorithm [J].IEEE Trans on Industrial Electro-nics,2014,61(7):3302-3312.

[9] 潘大志，刘志斌.量子粒子群算法的改进实现[J].计算机工程与应用,2013,49(10)：25-27.

[10] 袁晓琳，程 宇.自适应权重粒子群算法在阴影光伏发电最大功率点跟踪中的应用[J].中国电力，2013,10(10)：85-90.

[11] 刘衍民，牛 奔，赵庆祯，等.多目标优化问题的粒子群算法仿真研究[J].计算机应用研究，2011,2(2):458-460.

[12] Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proc of IEEE Int'l Conf on Neutral Networks，Perth，Australia，1995：1942-1948.

[13] Bouzid W.Cutting parameter optimization to minimize production time in high speed turning[J].Journal of Materials Processing Technology，2005，161：388-395.

Research and optimization on MPPT of PV systems under shading

WU Kun1， WANG Lei2， WANG Qiu-shi1， CHEN Dong1

(1.College of Electrical and Control Engineering,Liaoning Technical University,Huludao 125105,China;2.Zhejiang SolaX Power Co Ltd,Hangzhou 310000,China)

In order to solve the problem of unstable operation and output power decreasing of photovoltaic(PV) cells caused by partial shade due to leaves,buildings,clouds,etc,propose a maximum power point tracking(MPPT) of the shading condition PV systems based on GPPSO,and use it for MPPT of the complex shading condition PV systems.Results show that double optimized algorithm effectively improves the local accurate searching and global convergence ability of optimization space,in the process of the optimal solving of objective function,precision and convergence speed are improved obviously,which can rapidly adapt to environmental shade changes,can accurately track the maximum power point in complicated environment,and improve efficiency of PV systems.

photo voltaic(PV)systems; shade conditions; improved particle swarm optimization(PSO)algorithm; maximum power point tracking(MPPT)efficiency

10.13873/J.1000—9787(2017)07—0038—04

2016—08—08

TM 46

A

1000—9787(2017)07—0038—04

吴 琨(1991-)，男，硕士研究生，研究方向为电力电子变换技术，E—mail:wukun024@163.com。