基于GNSS-R的反演海面风速技术的研究

袁国良，张卫峰，卫豪杰

(上海海事大学，上海 201306)



基于GNSS-R的反演海面风速技术的研究

袁国良，张卫峰，卫豪杰

(上海海事大学，上海 201306)

对利用全球导航定位系统的海洋反射信号(GNSS-R)反演海面风速的方法进行了研究。GNSS-R技术作为一种新型的、低成本的海洋微波遥感测风技术，与其他测风技术相辅相成，弥补了某些测风手段的不足。文中还讨论了散射信号相关功率模型中的散射截面、多普勒区、等延时区、天线覆盖区四部分函数的定义和性质。使用Elfouhaily海浪谱模型，数值模拟了机载高度下散射信号相关功率的理论波形，在此基础上，又结合机载高度下获得的实测数据反演得到海面风速，反演得到的风速的均值与试验时浮标数据所对应的风速的均值比较相差1.4 m/s，误差在可接受的范围内，反演得到的风速与浮标数据相一致。

GNSS-R；海面风速；反演

0 引言

GNSS-R可以用于反演海面风速、海面测高、海冰的探测、海洋盐度的探测、土壤湿度的探测等。GNSS-R的技术特点是利用反射的导航卫星伪随机测距码信号或者载波信号，提取目标反射面特征，对于海面风场及移动目标探测等应用，其工作模型为收发分置的双基雷达模式，与传统的后向散射单基工作模式的卫星散射计和雷达高度计相比，其特点和优势集中体现为：(1)不用发射机，利用全球共享的GNSS星座为多元微波信号反射源；(2)大量的信号源，不仅利用目前已有的24颗GPS卫星，还有Galileo卫星、GLONASS卫星、中国北斗卫星系统等；(3)采用扩频通信技术带来的增益使得导航卫星反射信号接收机可以接收到低于背景噪声的微弱信号；(4)实时性强、全球覆盖、全天候等。

关于利用GNSS-R反演海面风速风向的研究，欧美国家起步较早。在过去的几年中，此技术逐渐趋近成熟。1993年，Martin-Neria率先提出了利用GNSS-R反演海面波高的概念，并且对其概念进行了系统性的理论描述[1]；1996年，美国兰利研究生中心研制出了用来测量反射信号的一种特殊的延时映像接收机(DMR),并用此接收机进行了机载实验[2]，将机载实验反演得到的风场和浮标数据与卫星数据进行对比，最后得出GNSS-R反演海面风速精度在2 m/s，风向精度在10°左右[3]。2000年Zavorotny 和 Voronovich[4]对双基结构的反射信号与海面风场的关系进行了理论分析，并建立了Z-V模型。为了验证GNSS-R与海面风场的关系，西班牙研究机构、美国国家海洋大气管理局、英国国家空间中心、欧洲空间局等机构均开展了关于机载、气球、星载的大量试验。

1 GNSS-R遥感风场与其他技术的比较

GNSS-R遥感风场与其他技术的比较如表1所示。

表1 GNSS-R遥感风场与其他技术的比较

2 GNSS-R海面风速探测机理

根据2000年Zavorotny 和 Voronovich建立的针对双基结构的GPS信号的前向散射模型—Z-V模型，经过几何光学近似可以得到海面散射信号相关功率模型，它是时间延迟τ和多普勒频移fc的表达式[5]：

(1)

其中，Rt(r)、Rr(r)分别是GPS卫星和接收机到散射点之间的距离；D(r)是散射点r处到天线的增益；Λ为自相关函数；S为多普勒频移函数；σ0(r)表示散射截面；Ti为相干积分时间。

风作用于海面时，会使海面产生表面波，此时海面的粗糙度将会发生变化。GNSS海面散射信号相关功率模型中的σ0与海面粗糙度有关，它将会影响散射信号相关功率模型的后沿斜率，如图1[6]所示。

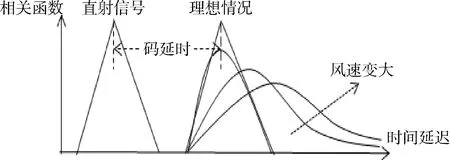
图1 不同海况条件下散射信号功率曲线

2.1 闪耀区

海面闪耀是与海面对太阳光反射相似的一种现象(如图2)，GPS卫星相当于太阳，接收机相当于人的眼睛。对于粗糙海面，一个更加宽广的海面可以产生指向接收机的辐射，这个有明显的微波反射的区域的海面被称为闪耀区。闪耀区的形状和大小受接收机的高度和海面粗糙度等因素的影响。闪耀区的定义如图3所示。在图3中，T、R、P分别为发射机、接收机、散射点的位置，PA为∠ZPR的角平分线，β为PA与Z轴的夹角，则定义镜面反射点[7]

图3 闪耀区的定义

O周围满足β≤β0的区域为闪耀区，其中β0=arctan(2σ/L)[8]，为描述海面粗糙度的常量，σ为海面高度标准偏差，L为波面相关长度[9]。

2.2 多普勒等值区

多普勒频移是由GPS卫星、接收机以及海面散射面之间的相对运动而产生的。观测区域内，具有相同多普勒频移的点组成的集合称为多普勒等值线。

对于在平均海面上，r端点处的多普勒频移为：

fD(r)=[Vt·m(r)-Vr·n(r)]/λ

(2)

fc用来补偿多普勒频移fD的本振频率，即镜面反射点处的多普勒频移为：

fc=[Vt·m(O)-Vr·n(O)]/λ

(3)

2.3 天线覆盖区

函数D(r)表示的是天线的增益，由于机载接收机的高度较低，所以此处使用的是全向天线增益，G2=1。

2.4 等延迟区

GPS信号经过海面反射到达接收机，观测区域内具有相同时延的点的集合称作等延时线。如果以镜面反射点O为参考点，就可以理解为Δτ=τ(r)-τ0=(Rt(r)+Rr(r))/c-τ0为常数的点的集合(τ0为镜面反射点处的时延)。

表达式(1)中的伪随机码自相关函数Λ,事实上表示的是伪随机码的卷积过程，如下定义：

(4)

3 海面风场反演流程

海面风场反演的方法通常是首先找到与实测相关功率的波形相匹配的理论相关功率波形，然后此理论波形所对应的风速就是实测的风速。主要依据是：风速越大，海面倾斜变化越大，海面越粗糙，反射信号的功率谱峰值越小，波形越扁平；反之，功率谱的峰值越高，波形越陡峭。因此提出了这种测量反射信号相关功率波形的方法来反演海面风速。如图(4)是海面风场反演的流程图。步骤如下：

(1)将接收机高度与速度、相干积分时间、卫星高度角等参数输入到海面散射信号相关功率模型，即式(1)，生成不同风速条件下的相关功率理论波形。

(2)由于天线环境因素的影响，实测数据中有噪声存在。因为镜面反射点处的信号最先到达接收机，故可以将早于镜面反射点2个码片的输出数据功率均值作为噪底。

(3)计算每个实测波形相对于镜面反射点的码延时，以确保实测波形与理论波形的时间延迟轴一致。

(4)分别对实测波形和理论波形进行归一化处理。归一化因子是总的反射信号功率，因为总的反射信号功率与海面统计特性无关，可近似为常量。

(5)采用最小二乘法将实测波形和散射信号相关功率的理论波形进行匹配，当两波形的后延的均方偏差达到最小时，理论波形对应的风速即为所求的海面风速。

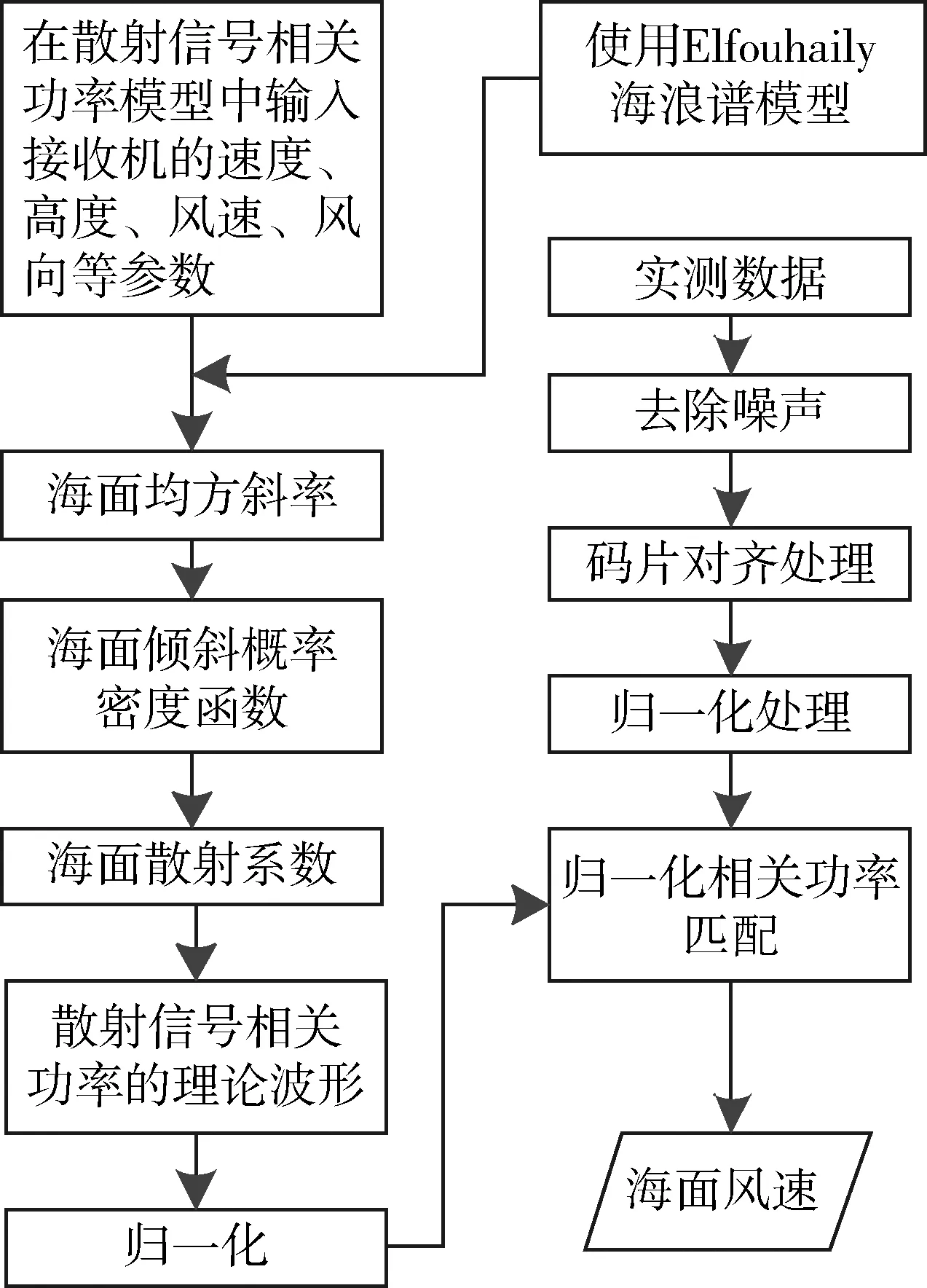
图4 风速反演流程

4 风速反演实例

本文以2004年9月11日的实验数据为例来进行海面风场反演。试验中，接收机的高度为4 000m，飞行速度为300m/s，该接收机是有6个反射通道的并行延时映像接收机，其采样频率是1Hz，每秒可记下32个离散时间延时下的相关功率值。

图5是接收机在17:00时采集到的PRN02卫星的反射信号功率和该时间的平均数据。此时，接收机的平均高度是3 942m，接收机的平均速度是293m/s，卫星的平均仰角是60.05°。

图5 实测PRN02卫星1 min的反射数据及平均值

图6是将测得的反射信号功率转化成分贝形式，并且与风速从5～14m/s的具有几何结构的理论波形进行比较。因为某些延时点的信噪比小于1，所以在减去噪声后再求对数时，结果为虚数，这就造成了数据不均匀的情况。但是，这并不影响风速的反演。从图中可以看出，实测数据的散射信号功率曲线与风速为5m/s的理论散射信号功率曲线较一致。因此通过实测数据反演得到的海面风速为5m/s。

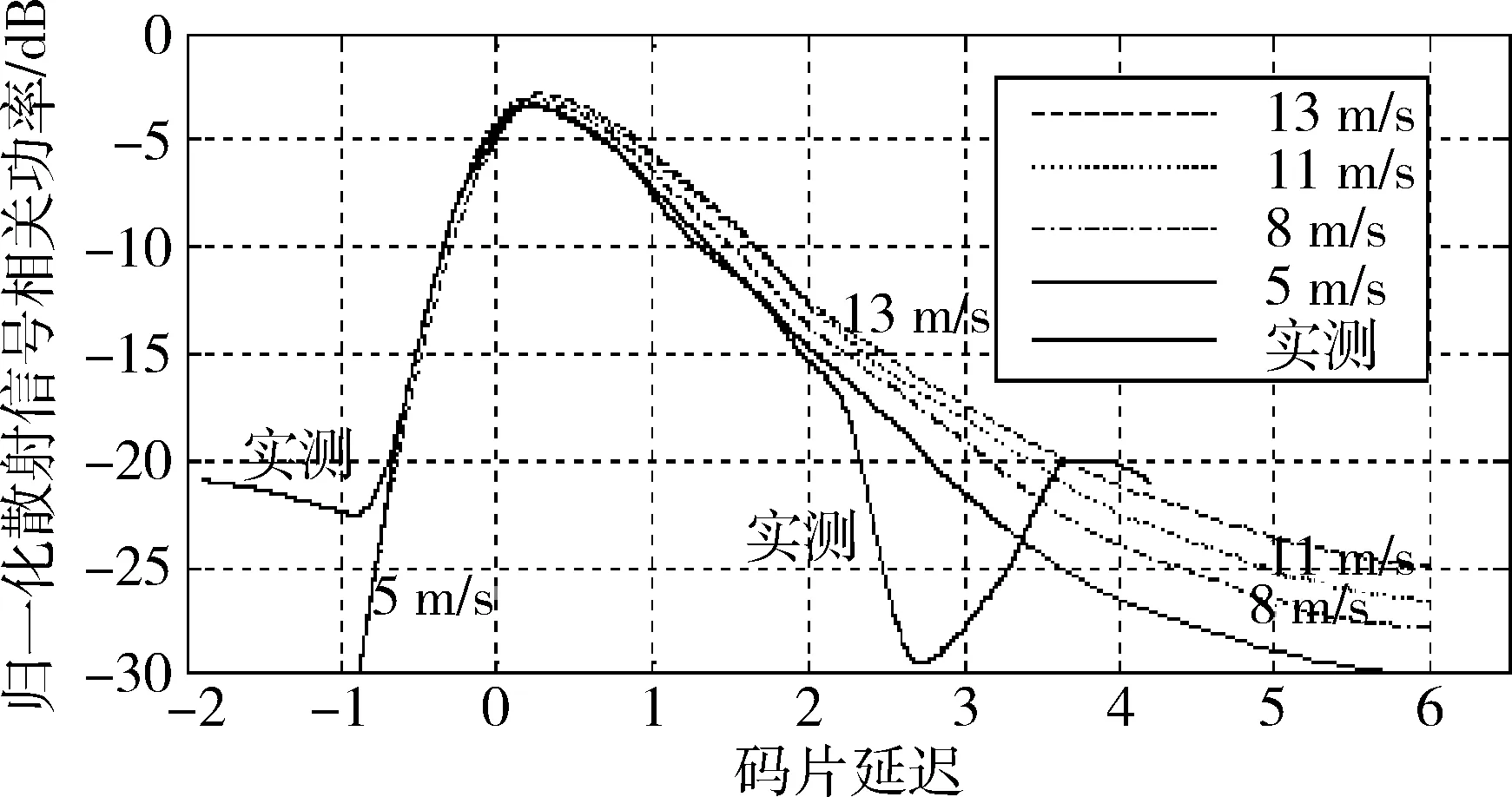
图6 实测波形与理论波形对比

5 结果检验

使用上述的风速反演方法和流程，以1min平均相关功率波形为实测值反演得到的海面风速值与试验所记录的浮标值得到的风速相对应，如图7所示。由图可看出浮标测得的风速值与GNSS反演得到的风速值有较好的吻合，在测量的这段时间里，反演风速的均值为5m/s，浮标得到的风速均值为6.4m/s，相差1.4m/s。误差在可接受的范围内。

图7 浮标风速值与反演得到的风速值的比较

6 结束语

GNSS-R作为一种新型的遥感技术，用来反演海面风速在理论上和实践上都是可行的。由于海浪谱模型[10]对风速的局限性，GNSS-R反演海面风速技术只适应于中低风速的条件(≤20 m/s)，当风速超过这个范围时，反演较困难。接收机收到的经过海面散射后的GNSS信号非常微弱，这对接收机的增益和噪声处理要求较高。因此研制更好的接收机非常关键。

[1] MARTIN-NERIA M. A passive reflectoetry and interferometry system(PARIS): application to ocean altimetry[J]. ESA Journal,1993,17: 331-355.

[2] AUBER J C, BIBAULT A, RIGAL J M. Characterization of multipath on land and sea at GPS frequencies[J]. Geoph Ysical Research Letters, 2013, 25(13): 2257-2260.

[3] KOMJATHY A, ARTMATYS M, MASTERS D. Developments in using GPS for ocean ographic remote sensing: retrieval of ocean surface wind speed and wind direction[J]. IEEE Transaction on Geoscience and Remote Sensing, 2011, 48(2): 956-962.

[4] ZAVOROTNY V U, VORONOVICH A G. Scattering of GPS signals from the ocean with wind remote sensing application[J]. IEEE Transaction on Geoscience and Remote Sensing, 2014,38(2): 951-964.

[5] GLEASON S, ADJRAD M, UNWIN M. Sensing ocean ice and land reflected signals from space: results from the UK-DMC GPS reflect ometry experiment[J].GPS World,2010,10(4): 50-56.

[6] 路勇.基于GNSS反射信号的海面风速探测技术研究[D].北京：北京航空航天大学,2009.

[7] WU S C, MEEHAN T, YOUNG L. The potential use of GPS signals as ocean altimetry observable[C]. Proceedings of the National Technical Meeting of the Institute of Navigation, 1997.

[8] APOSTOL B F. Scattering of the electromagnetic waves from a rough surface[J]. Journal of Modern Optics, 2012, 59(18): 1607-1616.

[9] GARRISON J L,KATZBERG S J, HOWELL C T. Detection of ocean reflected GPS signals: theory and experiment[C]. The IEEE Southeastcon, Blacksburg,1997: 256-258.

[10] EIFOUHAILY T,CHAPRON B,KATSAROS K,et al. A unified directional spectrum for long and short wind- driven waves[J].Journal Geophysical Research,1997,102(C7):15781-157961.

Sea surface wind speed measurement using GNSS reflection signal

Yuan Guoliang, Zhang Weifeng, Wei Haojie

(Shanghai Maritime University, Shanghai 201306, China)

This paper introduces the mechanism of sea surface wind speed measurement using GNSS reflection signal. GNSS-R technology is a new, low-cost microwave remote sensing technology of ocean wind measurement.This technology complementarity with other wind measurement technology and make up for the shortcomings of some wind measurement technology. This article also discusses the definition and natures of the scattering cross section, Doppler area, peer delay area, the antenna coverage area four parts function in the scattering signal correlation power model. This paper uses Elfouhaily wave spectrum model to simulate the theoretical waveform of the scattering signal power under the airborne height. On this basis and also combined the measured data obtained from the airborne height to get the inversion wind speed whose mean value has a difference of 1.4 m/s compared with the buoy data of wind speed when in testing.The difference is in the range of acceptable error and the inversion wind speed is consistent with the buoy data.

GNSS-R; sea surface wind speed; retrieval

TP79； P228.4

A

10.19358/j.issn.1674- 7720.2017.13.027

袁国良，张卫峰，卫豪杰.基于GNSS-R的反演海面风速技术的研究[J].微型机与应用，2017,36(13)：88-90，93.

2017-01-10)

袁国良(1963-)，男，副教授，主要研究方向：通信与信息系统化、光电通信。

张卫峰(1991-)，男，硕士，主要研究方向：基于GNSS-R的反演海面风速技术的研究、人体摔倒状态识别。

卫豪杰(1990-)，男，硕士，主要研究方向：基于GNSS-R的反演海面风速技术的研究。