吊舱推进的小型水面无人船航迹控制系统设计

燕聃聃,文元桥,肖长诗,张帆,周春辉

(武汉理工大学 a.航运学院; b.内河航运技术湖北省重点实验室, 武汉 430063)



吊舱推进的小型水面无人船航迹控制系统设计

燕聃聃,文元桥,肖长诗,张帆,周春辉

(武汉理工大学 a.航运学院; b.内河航运技术湖北省重点实验室, 武汉 430063)

为解决适应内河通航环境的小型水面无人船(USV)航迹控制的快速性和鲁棒性问题，以小型水面无人船为研究对象，设计一种基于吊舱推进的USV航迹控制系统，该航迹控制系统由航迹控制器、航向控制器、转向操作机构、电罗经、D-GPS，以及角度检测传感器组成。其中航迹控制采用改进的LOS(Line of Sight)导航算法；航向控制器由两级模糊控制器构成，可同时满足大角度转向控制和小角度航向保持的性能要求。仿真和实船试验结果皆表明，该控制系统能够满足内河复杂通航条件下USV对航迹控制的要求。

USV；LOS；模糊控制；航迹控制；吊舱

由于内河水域船舶通航密度大，航道弯曲，浅窄航段较多，气象和水文环境复杂，对无人船航迹控制的要求很高。考虑到船舶操纵模型具有时变、非线性、时滞性和不确定性，以及内河通航环境的复杂性，模糊控制以其不需建立被控对象精确模型的优点被多数人采用[1-6]。与传统的螺旋桨推进方式相比，吊舱推进具有机动性好、推进效率高、布置空间小等优点[7]，更适合内河水域船舶使用。针对吊舱推进式水面无人艇，以武汉理工大学iNav-Ⅰ无人船为研究对象，利用间接航迹控制方法设计船舶航迹控制系统。

1 系统原理

1.1 吊舱推进航迹控制系统基本框架

航迹控制系统原理见图1。系统由2个闭环即航迹控制环(制导环)和航向控制环组成。航迹控制环将船位反馈装置接收的船位信息与计划航线比较，获得船位偏差信息，通过制导算法得到命令航向作为航向控制环的期望值，用以消除航迹偏差；航向控制环将航向反馈装置接收的航向信息与命令航向比较，求出舵令给船舶以消除航向偏差，从而实现船舶航迹控制。

1.2 吊舱推进航迹控制系统机械结构

控制系统机械结构见图2。

图1 系统基本框架

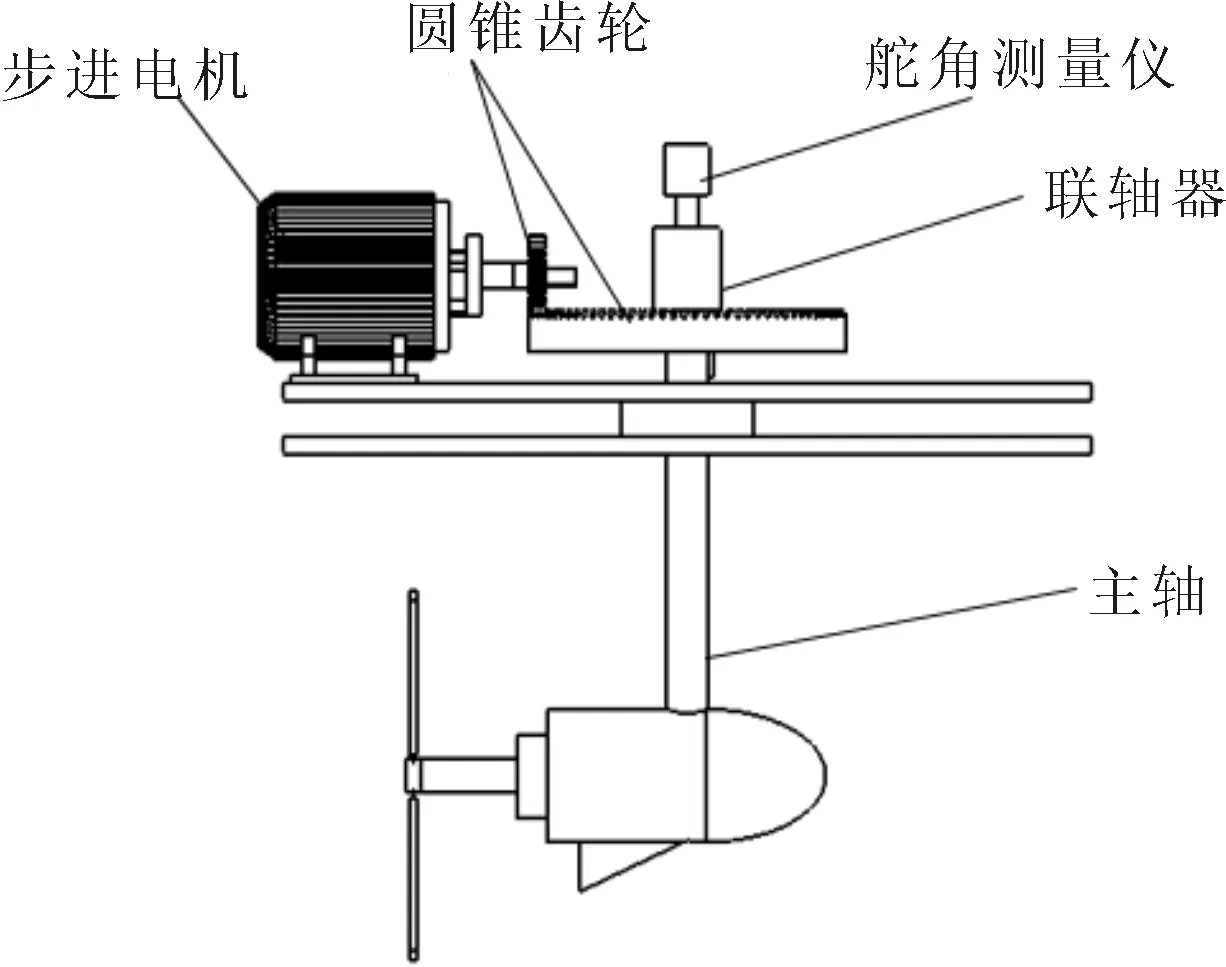
图2 控制系统机械结构示意

吊舱推进系统具有垂直贯穿于无人艇尾部甲板的主轴，主轴顶端装有舵角测量仪，可直接测量舵角。舵角测量仪下面的主轴上套装有联轴器，联轴器连接有圆锥齿轮，大小齿轮齿数比为5∶1，圆锥齿轮中的小齿轮连接有步进电机。步进电机与控制器构成驱动连接。主轴位于甲板下方的轴体上连接有吊舱，吊舱内置驱动电机，驱动电机输出轴通过传动轴连接螺旋桨。系统由步进电机提供转向驱动力，吊舱内置驱动电机提供前进动力。

2 无人船航迹控制数学模型

2.1 响应型非线性无人艇数学模型

无人船转艏运动一阶非线性K-T方程为

(1)

式中：T为稳定性指数；K为回转性指数；α为非线性系数。

考虑到横向速度较小，其平面运动数学模型[8]可简化为

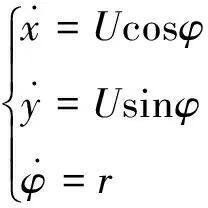
(2)

式中：(x,y)为重心坐标；φ为艏向角；U为船前进合速度；r为偏航角速度。

2.2 吊舱系统数学模型

吊舱推进航迹控制系统中，由步进电机给舵系统提供转向驱动力。吊舱系统数学模型的建立主要取决于步进电机的转速n、从上位机发出舵角控制命令到下位机控制单元接收到命令的时间t1，从下位机发出控制指令到步进电机开始反应的时间t2，从步进电机开始转动到吊舱转至设定值的时间t3。

假设期望吊舱转向角的值为δpre，初始吊舱转向角为δ0，且步进电机转速一定，那么吊舱从δ0转到δpre的时间为

(3)

经过实际测量计算，t1的数量级为100 ms，t2的数量级为10 ms。

3 航迹控制

3.1 航迹控制器

采用改进LOS(line-of-sight)导航算法，通过目标位置求得船舶的航向指令，船舶只要跟踪指令航向即可有效地保持航迹。其实质就是把航迹划分成一系列直线航迹段，当作直线航迹控制来对待，从而相应地简化航迹控制器设计的复杂程度。原理见图3，将船舶的航迹看成由关键点[X(k),Y(k)](k=1,2,3,…,N)组成的折线。

图3 改进的LOS算法示意

d为t时刻船舶位置[x(t),y(t)]与计划航线的距离。

1)如果满足d>l,那么船舶的期望航向为

(4)

2)如果满足d≤l,那么船舶的期望航向为

(5)

当船舶位置位于以关键点为圆心，ρ0为半径的圆域时，对k值进行更新。

3.2 航向控制器

采用的航向控制器由2级模糊控制器[9]构成，当航向偏差(Δφ)大于某一角度时，采用第一级模糊控制器控制，实现船舶快速转向；当航向偏差(Δφ)小于某一角度时，采用第二级模糊控制器控制，实现精确转向。

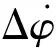
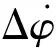
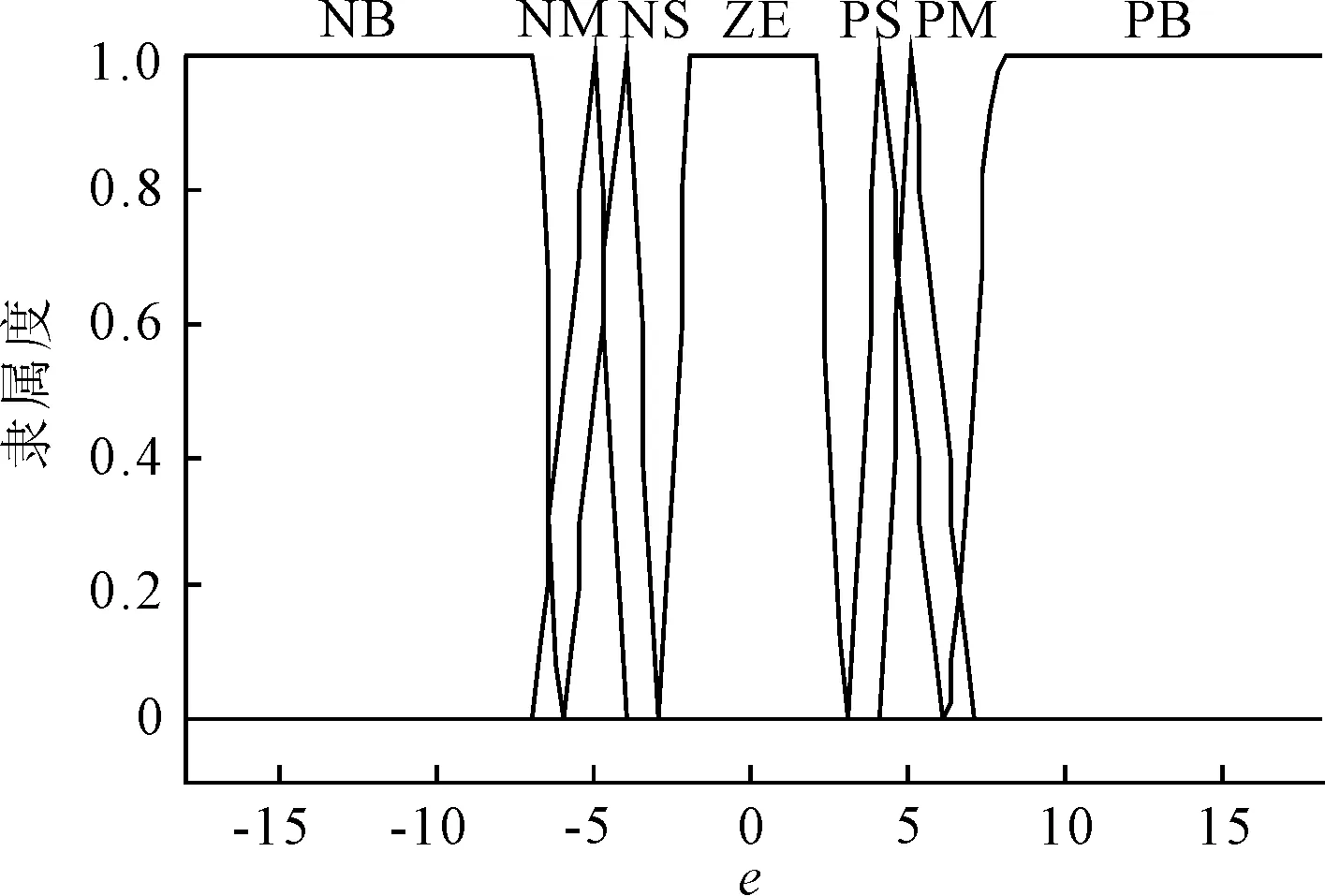
图4 e的隶属函数

图5 ec的隶属函数

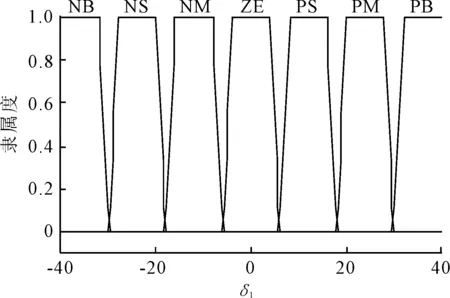
图6 δ1的隶属函数

输出δ1的隶属函数见图6，论域[-35,35]。模糊规则见表1。

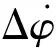
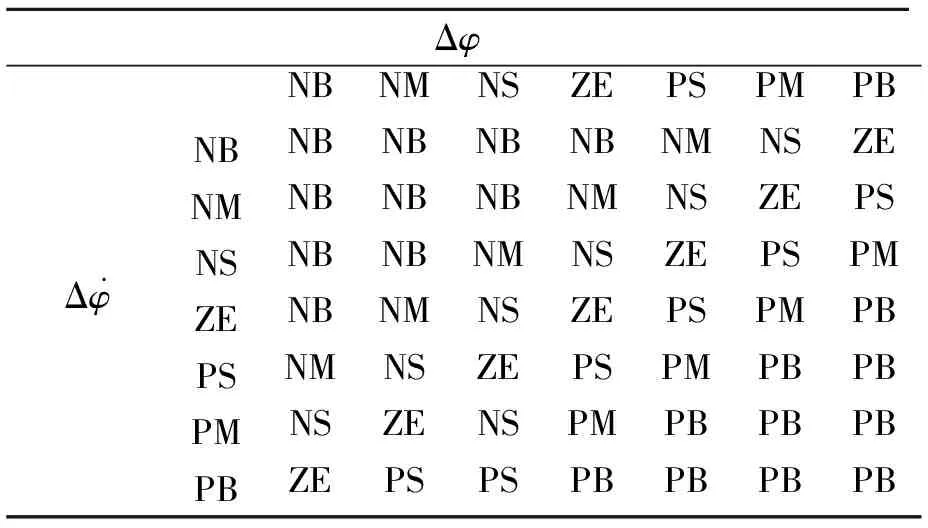
表1 第一级模糊控制规则

2)第二级模糊控制器。由于第一级模糊控制器输入为偏差和偏差变化率，存在控制死区，会产生控制误差，需要增加一个积分环节。如果只用一级模糊控制器，也就是说第一级模糊控制器中采用三输入，即偏差、偏差变化率、偏差积分，那么模糊规则将有7×7×7=343条。如果采用双极控制器，并且第二级控制器由一个模糊PD控制器和一个模糊PI控制器，那么模糊规则数量将大量减少，并且能够消除部分误差，获得较好的控制效果。模糊PD控制器输入的隶属度函数见图7、8，量化因子分别为0.133和0.02。输出的隶属度函数见图9。控制规则与第一级模糊控制器相同。

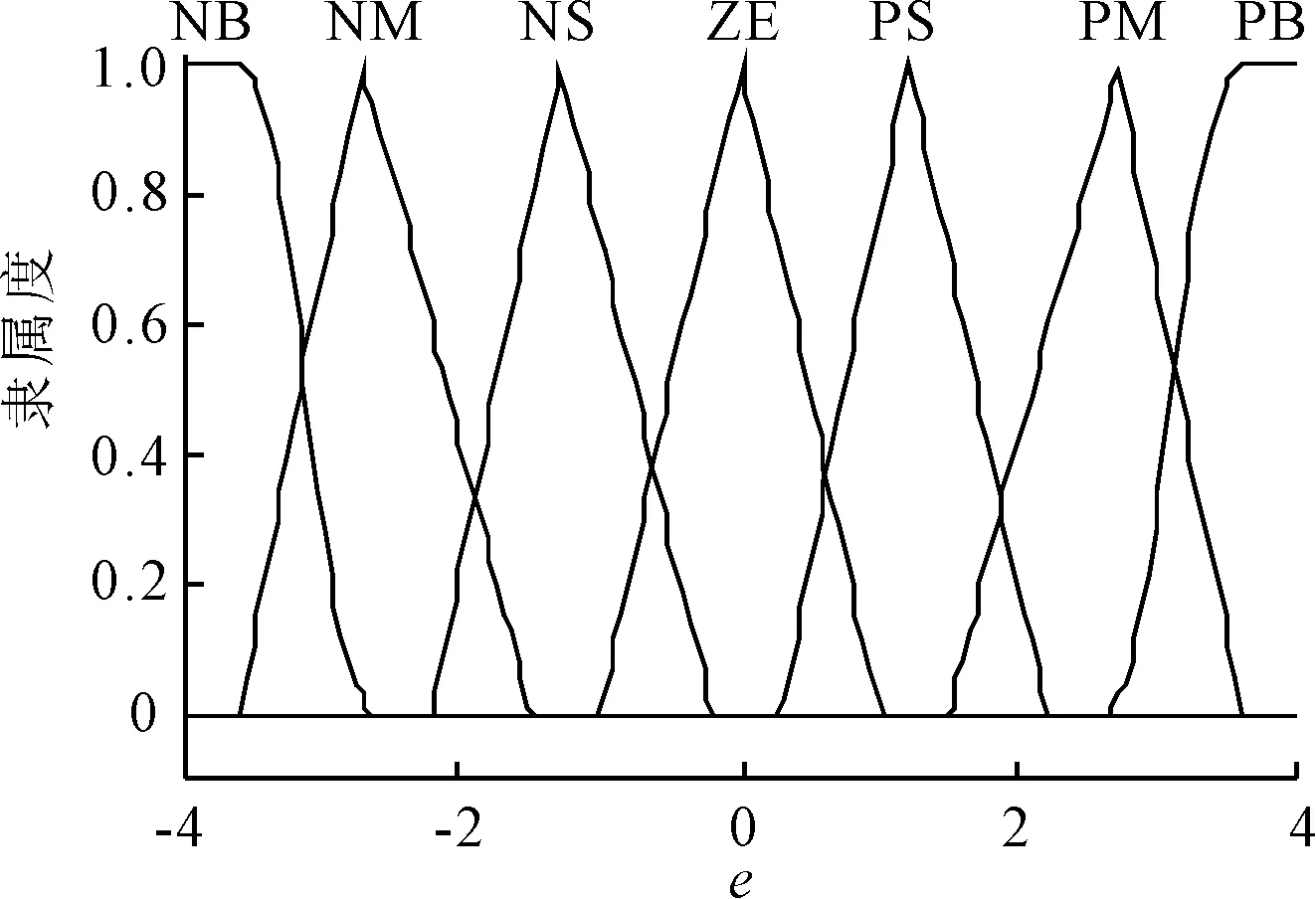
图7 Δφ的隶属度函数

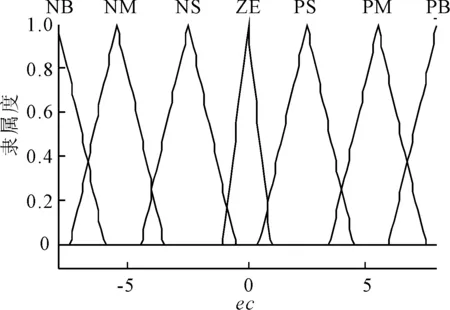
图的隶属度函数

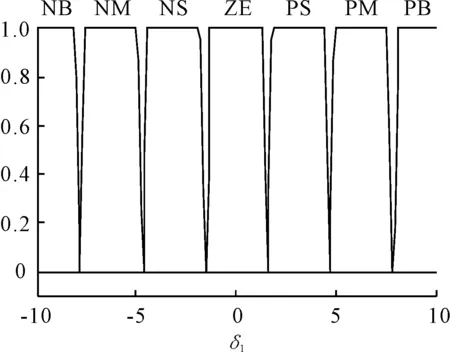
图9 δ21的隶属度函数

模糊PI控制的输入为航向偏差Δφ和航向偏差积分，将Δφ，∫Δφ和输出控制量的数量范围划分为5个语言变量表述的模糊集，即负大(NB)、负小(NS)、零(ZE)、正小(PS)、正大(PB)。∫Δφ的论域为[-8,8]，量化因子为0.02。输出量δ22的论域为[-10,10]。其隶属函数见图10～12。模糊规则见表2。

图10 Δφ的隶属函数

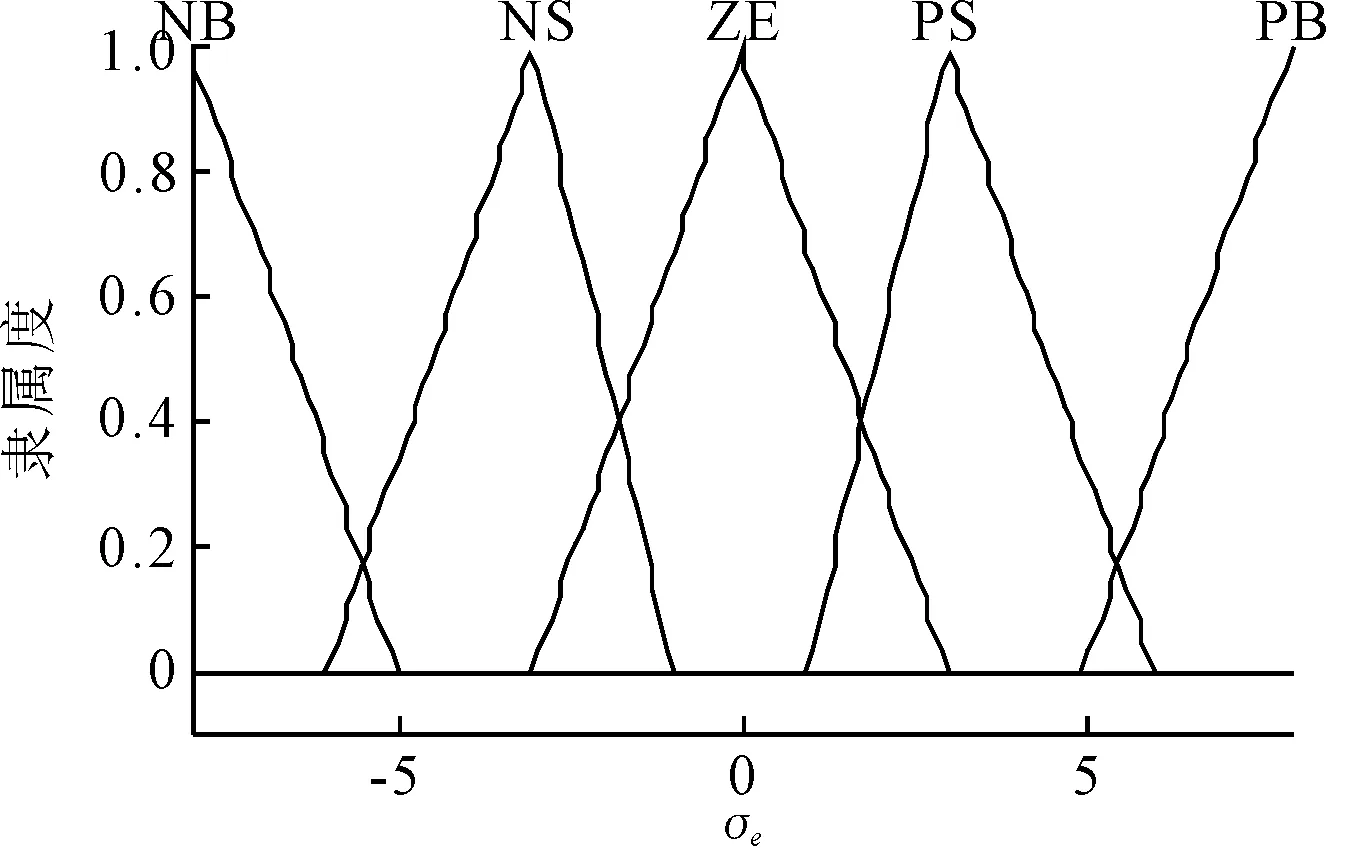
图11 ∫Δφ隶属函数

图12 δ22的隶属函数

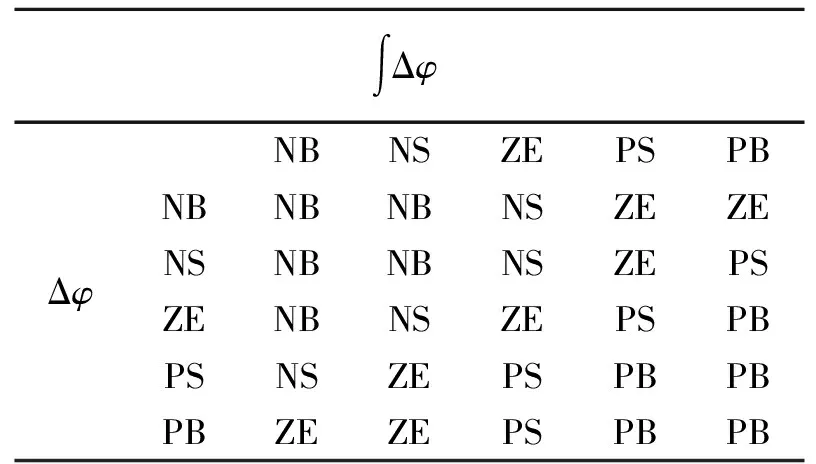
表2 第二级模糊控制器模糊积分控制规则

4 仿真实验

为了验证无人船航迹控制系统的控制效果，选择武汉理工大学iNav-Ⅰ无人船进行航迹跟踪控制实验，无人船相关参数见表3。

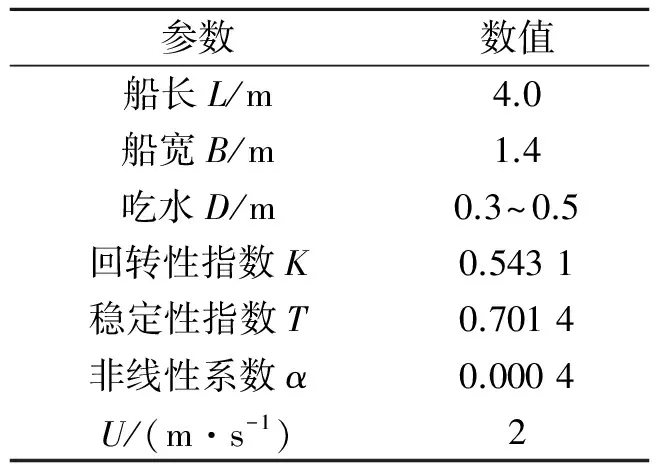
表3 iNav-I无人船基本参数

表中参数K、T由Z型实验和旋回实验结果进行参数辨识求得。无人船的初始位置为坐标原点(0,0)，初始艏向角为正北方向，ρ0和l都取值5 m。无人艇的航路点设置见表4。

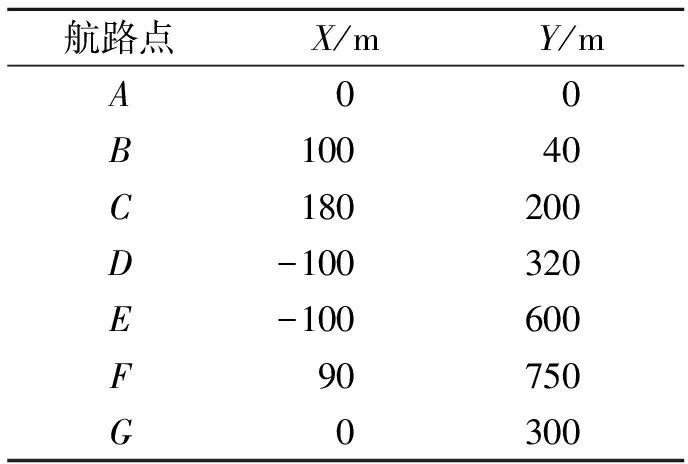
表4 设计航路点

为了使得仿真效果更真实，加入风浪流的干扰。将海流的干扰作用等效为10°的恒值干扰，风浪的干扰作用则通过白噪声和一个二阶波浪传递函数来模拟。

设定仿真海况为风力四级，大浪，具体参数[10]为Kω=0.1979,σm=0.544，ω0=0.606。仿真结果见图13～15。

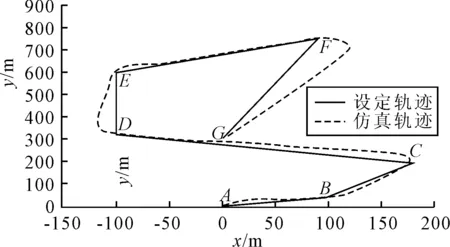
图13 干扰条件下的无人船航迹保持轨迹

图14 干扰条件下控制器的输出舵角

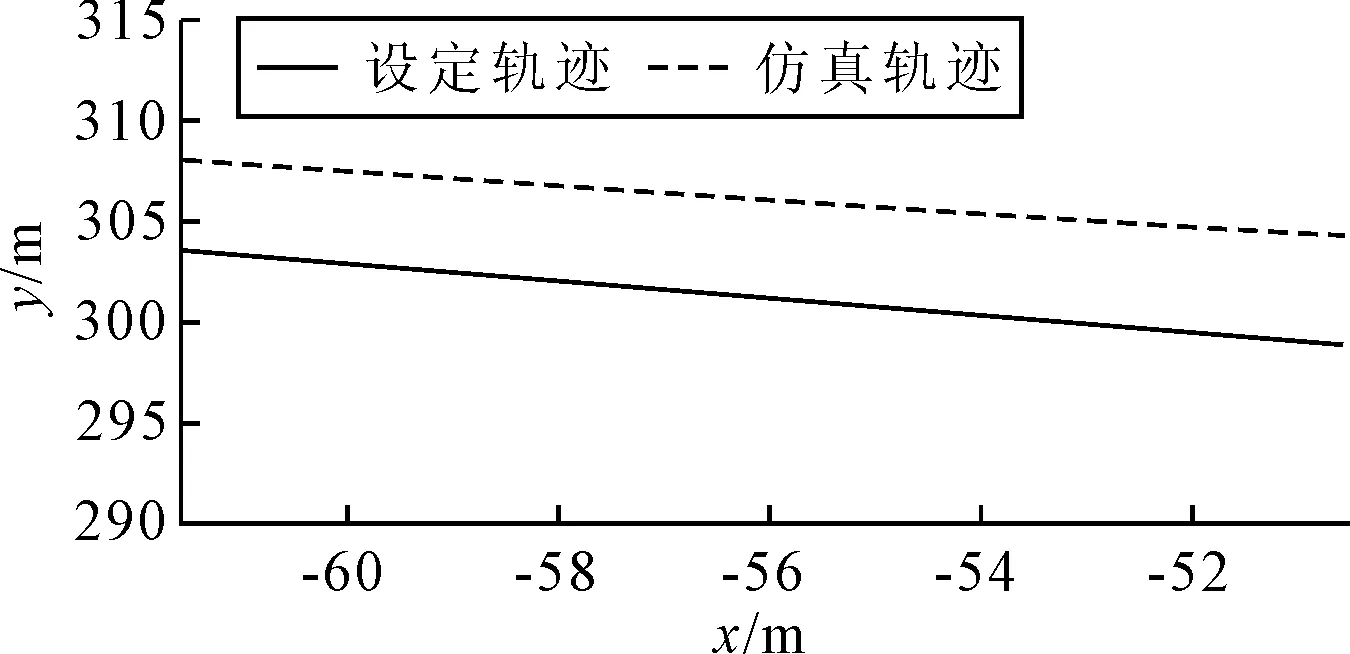
图15 有干扰条件下局部放大航迹

根据以上仿真结果可以看出，在上述干扰条件下，所设计的基于双极模糊控制和改进LOS航迹制导的航迹控制器基本能够完成航迹控制任务。由图13可见，无人船能够沿着设定航迹航行。在稳定阶段，航迹与设定航迹的垂直误差约为5 m，这个距离刚好与改进LOS算法中d的距离相同，说明航迹控制效果良好。但是在转向点F附近转向时，转向角较大，有将近30 m以上的误差。分析其原因，一方面由于d设置为5 m，只有当无人船在距离F点5 m的圆域内，才判定无人船到达F点，继而进行转向，打舵时间较晚；另一方面由于吊舱式推进器的响应具有一定的延时，实际舵角并没有达到控制器的输出值。

由图14可见，无人船舵角的变化规律是：无人船在转向角进行转向时，会先打出较大舵角，在转向即将结束时，航向逐渐趋于稳定，无人船的舵角也趋向于0°，基本符合实际情况。

6 实船验证

无人船航迹控制的实船试验在武汉东湖水域进行，试验中船舶的平均航速1 m/s，湖面稍有风浪。

设定航迹关键点见表5。

进入航迹控制后，无人船的运动轨迹见图16。

表5 设计航路点

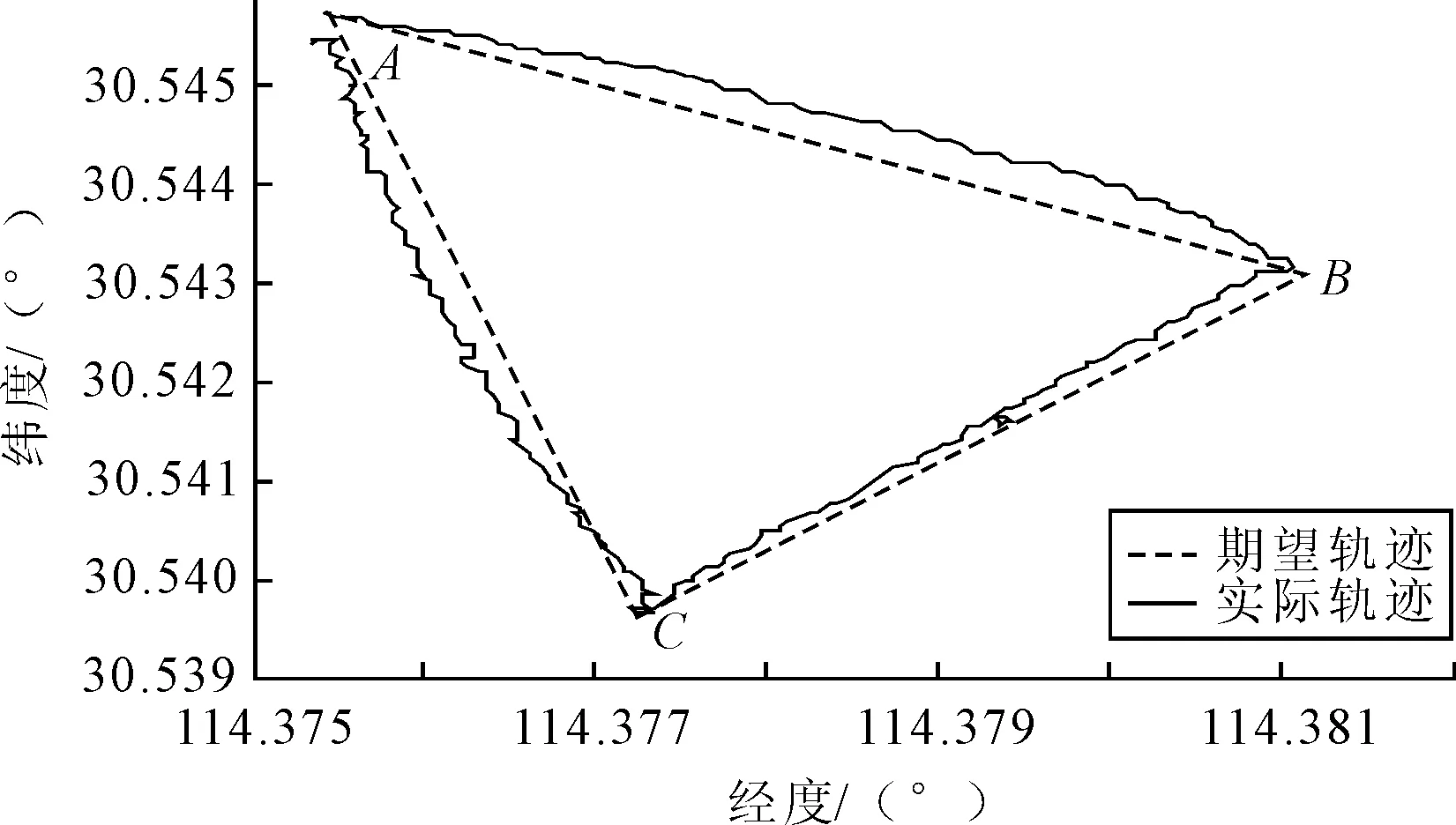
图16 无人船航迹控制实船试验结果

由图16可见，所设计的航迹控制器在实际中可以完成航迹控制目标，说明所设计的间接控制系统是有效的，可行的。但就控制效果而言，AB段和CA段误差较大，最大误差甚至达到43 m左右，BC段误差较小，但最大也有20 m。

7 结论

1)以吊舱推进型小型无人船为研究对象，采用改进的LOS制导算法和双极模糊算法对船舶航迹控制进行系统研究，并应用于实船实验中，为解决内河环境下无人船路径规划、避碰等问题奠定了理论和实践基础。

2)仿真时，当转向角较大时，航迹偏差较大，一方面与ρ0值相关，另一方面由于模糊规则和隶属函数一旦确定，便不可调节，下一步应从这两方面进行改进。

3)针对实船实验误差较大的问题，可考虑增加舵角控制环，对吊舱的转向进行反馈控制，便于进一步减小误差。

[1] VUKIC Z, OMERDIC E, KULJACA L. Improved fuzzy autopilot for track-keeping[C]. Proceedings of the IFAC Conference on Control Applications in Marine Systems.1998.

[2] OMERDIC E, ROBERTS G N, VUKIC Z. A fuzy track-keeping autopilot for ship steering[J]. Journal of marine engineering and technology,2003(2):23-35.

[3] FRAGA R, SHENG L. Double fuzzy logic control for the ship path following[C]. Intelligent Control and Information Processing(ICICIP),2011 2ndInternational Conference on. IEEE,2011.

[4] FRAGA R, SHENG L. Fuzzy technique tracking control for multiple unmanned ships[J]. Research Journal of Applied Sciences,2013,5(2)：538-545.

[5] 郝阳,赵新华.船舶航迹自校正模糊自动驾驶仪设计[J].控制工程,2014(增刊1):73-75.

[6] 董早鹏,刘涛,万磊,等.基于Takagi-Sugeno模糊神经网络的欠驱动无人艇直线航迹跟踪控制[J].仪器仪表学报,2015,36(4):863-870.

[7] 马骋.吊舱推进技术[M].上海：上海交通大学出版社，2009.

[8] 王波.基于滑模的船舶直线航迹控制设计及优化[D].大连：大连海事大学,2014.

[9] YAN Dandan, XIAO Changshi. Pod propulsion small surface USV heading control research[C].Proceedings of the International Offshore and Polar Engineering Conference.2016：630-635.

[10] 葛增鲁.无人艇航向运动控制器的设计与实现[D].大连：大连海事大学，2016.

Development of Tracking Control System for the Pod Propulsion Small Surface USV

YAN Dan-dan, WEN Yuan-qiao, XIAO Chang-shi, ZHANG Fan, ZHOU Chun-hui

(a.School of Navigation; b.Hubei Key Laboratory of Inland Waterway Transport Technology;Wuhan university of technology, Wuhan 430063, China)

To solve the problems of speed and robustness of track control for small unmanned surface vehicle (USV) in the inland water navigation environment, a USV track control system was designed based on the pod propulsion, which was compose of track controller, course controller, steering mechanism, electronic compass, D-GPS and rudder angle measuring instrument. The improved LOS (Line of Sight) navigation algorithm was used by the track controller. The heading controller included two fuzzy controllers, which can meet the requirements of large-angle steering control and small-angle course keeping. The simulation results of real ship sailing experiments showed that this control system can meet USV’s requirement of track control under complex conditions of inland navigation.

USV; LOS; fuzzy control; track control; POD

10.3963/j.issn.1671-7953.2017.04.048

2016-12-05

国家自然科学基金(51579204)

燕聃聃(1992—)，女，硕士生

研究方向：智能航海与船舶控制

U675.79

A

1671-7953(2017)04-0210-06

修回日期：2017-01-18