基于同态滤波与Curvelet变换的钻孔图像自适应增强*
何飞佳, 李庆武,2, 韩 辉, 张建清, 谭显江
(1.河海大学 物联网工程学院,江苏 常州 213022;2.常州市传感网与环境感知重点实验室,江苏 常州 213022;3.长江地球物理探测(武汉)有限公司,湖北 武汉 430010)
基于同态滤波与Curvelet变换的钻孔图像自适应增强*
何飞佳1, 李庆武1,2, 韩 辉1, 张建清3, 谭显江3
(1.河海大学 物联网工程学院,江苏 常州 213022;2.常州市传感网与环境感知重点实验室,江苏 常州 213022;3.长江地球物理探测(武汉)有限公司,湖北 武汉 430010)
针对岩石数字钻孔图像存在的光照不均、图像中岩石表面边缘细节模糊等情况,提出了一种钻孔图像自适应增强算法。对原图进行同态滤波;使用Curvelet变换分解原图与滤波后的图像,对两者的低频子带使用系数直方图匹配算法,将前者与后者的直方图进行匹配,改善光照不均的影响;对原图的高频子带使用自适应的阈值进行滤波,同时利用自适应增强函数进行增强;使用Curvelet反变换重构得到增强后的图像。实验结果表明:算法可以有效地改善钻孔图像光照不均的问题,增强图像中物体的边缘信息,在主观视觉效果和图像客观评价指标上相对于其他算法均有一定优势。
钻孔图像; 图像增强; Curvelet变换; 系数直方图匹配; 自适应增强
0 引 言
钻孔电视技术被广泛应用于工程地质、岩土工程、土木工程等多个领域[1]。在实际应用中,由于拍摄条件限制以及岩石表面凹凸不平等原因,岩石钻孔图像通常存在光照不均、图像中物体边缘细节模糊等情况,图像中光照强的高光区细节信息失真,而光照弱的暗光区细节信息较难显现。
为了消除光照不均的影响,同时提高图像局部细节信息,需要对图像进行增强处理。图像增强方法主要分为基于空域和基于频域两大类。空域增强算法虽能提高图像整体对比度,但会降低图像高光区和暗光区的灰度值区分度,造成两类区域细节信息丢失。频域图像增强方法的主要思想是将图像分解为低频子带与高频子带,通过对含有大量图像基本信息的低频子带增强以提高图像对比度,同时抑制高频子带中含有的噪声并且增强图像边缘细节信息。Curvelet变换属于频域算法[2~7],由Candes E J和Donoh D等人在小波变换的基础上提出的一种新的多尺度几何分析方法,具有各向异性的特点,对图像几何特征有更强的表达能力,能够很好地提取图像边缘特征。
同态滤波对改善光照不均的图像对比度具有良好的效果,但同时也会模糊图像纹理细节。经Curvelet分解后,图像概貌主要反映在Curvelet低频系数上,图像纹理细节主要反映在Curvelet高频系数上。鉴于此,本文提出了一种基于同态滤波和Curvelet变换系数直方图匹配的钻孔图像自适应增强方法,以同态滤波处理后图像的系数直方图为基准,将原图分解所得的低频子带系数直方图匹配于前者,改善原图中光照不均问题,同时保留了纹理细节;对原图分解所得的高频子带使用自适应增强算法,增强图像边缘纹理信息,最终实现了岩石钻孔图像的自适应增强。
1 Curvelet变换


图1 Curvelet变换频带划分示意图
本文采用基于“Wrapping”频域特殊采样的卷绕规则方法,即,形式的快速离散Curvelet变换算法[9],其步骤如下:
1)将图像看作笛卡尔坐标系下的二维函数f,对f进行二维快速傅里叶变换(FFT)计算得到;
2 基于同态滤波和Curvelet变换系数直方图匹配增强
2.1 同态滤波
当用f(x,y)二维函数形式表示空间域图像时,可以由2个分量表征:入射光源总量i(x,y)和物体反射光的总量r(x,y),即
f(x,y)=i(x,y)·r(x,y)
(1)
考虑到所获得的钻孔图像可看作外部光源的入射光与岩石表面的反射光两者的乘积,由此引入同态滤波来改善图像中光照不均的问题,通过适当降低入射量函数i(x,y)的影响,同时增强反射率函数r(x,y)的频谱成分达到增强岩石钻孔图像的目的。具体流程如图2所示。

图2 同态滤波流程
其中,影响高频与低频分量的高通滤波器设计如下

(2)
式中rH,rL分别为高通截止频率和低通截止频率;d(u,v)=[(u-u0)2+(v-v0)2]1/2为频率(u,v)到滤波中心(u0,v0)的距离;C和D共同决定了高斯滤波器的频率宽度。
2.2 低频子带系数直方图匹配
设c为归一化至区间[0,1]的原图Curvelet低频子带C0中的系数,d为归一化至区间[0,1]的同态滤波后图像的Curvelet低频子带D0中的系数,ck和dq分别为系数c和系数d经量化级数为L的均匀量化后的系数。pc(ci)为ck中第i个系数个数ni占ck中系数总数n的比例,pd(di)为期望输出的系数直方图所具有的概率密度函数。对ck和dq均进行一次均衡化处理,得到以下2个累积分布函数,即

(3)
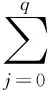
(4)
根据直方图匹配的原理[11],有G(dq)=T(ck),因此,dq必须满足条件
dq=G-1(sk)=G-1[T(ck)]
(5)
即将原图对应低频子带中的每个均衡后的系数值sk映射为直方图匹配后的低频子带中的相应dq值。经系数反归一化后,最终得到直方图匹配后的低频子带结果。
2.3 高频子带系数的自适应增强
经Curvelet分解后,高频子带部分包含大量图像边缘信息与噪声,如果直接对其进行增强,那么噪声也随之增强。因此,这里需要设定一个阈值 ,将大于阈值的高频子带系数视为边缘细节信号,并进行增强处理;将小于阈值的高频子带系数视为噪声,并进行衰减处理,即可以实现对数字钻孔图像边缘细节信息进行增强,提高清晰度,同时具有降低噪声的作用。
在Curvelet变换系数中大部分噪声处于最细子带。在最细子带中采用经典中值估计公式σ=median[abs(Ct)]/0.674 5对方差σ进行估计。其中,Ct为Curvelet分解后的最细子带系数。阈值设定为
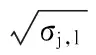
(6)
式中σj,l为第j尺度,第l方向的噪声方差,其值可由蒙特—卡洛估计法得到。
利用如下自适应增强函数[12]进行相应的系数调整

(7)

2.4 算法实现步骤
数字钻孔图像自适应增强算法步骤:
1)获取钻孔图像I,并进行同态滤波,得到图像J。
2)对I进行Curvelet变换,分解得到低频子带系数矩阵C0,以及其余高频子带系数Cj,l计算低频子带系数矩阵C0的系数直方图HC0以及Cj,l的系数直方图HCj,l。
3)对J进行Curvelet变换,分解得到低频子带系数矩阵D0,以及其余高频子带系数矩阵Dj,l。然后计算D0的系数直方图HD0以及Dj,l的系数直方图HDj,l。
4)低频子带系数直方图匹配:以图像J为基准,将步骤(2)中得到的C0的系数直方图HC0匹配到步骤(3)中得到的D0的系数直方图HD0上。
5)高频子带系数自适应去噪增强:估计步骤(2)得到的高频最细子带系数矩阵C各方向的噪声水平,按照式(6)设定阈值T,将Cj,l值小于阈值T的部分滤除,大于阈值T的部分利用式(7)对其增强得到系数矩阵j,l。
6) 对所有子带系数进行Curvelet逆变换,得到增强后的图像。
3 实验结果与分析
为验证算法针对数字钻孔图像的有效性,利用本文提出的基于Curvelet变换的钻孔图像自适应增强方法分别与双向直方图均衡[12]、同态滤波算法、非下采样Contourlet变换(NSCT)域自适应增强算法、Curvelet域增强算法等4种算法进行比较。其中图3(a),图4(a)分别为某地区1号、2号场地的钻孔图像。下列钻孔图像的分辨率均为944 pixel×944 pixel。
实验环境:Intel Core i5—2450 CPU,8 GB内存,64位win7操作系统, Matlab8.1.0(R2013a)。实验参数设置如下:同态滤波增强算法利用式(2)计算,取rH=4,rL=1.02,C=1,D=2。NSCT域自适应增强算法利用文献[4]给出的算法计算。Curvelet增强算法利用文献[7]给出的算法计算,其中,低频子带增强模块取a=2,b=4,高频子带增强模块取b=0.13,c=10,d=0。本文算法中的同态滤波参数值设置同上。

图3 1号场地钻孔图像及5种增强结果
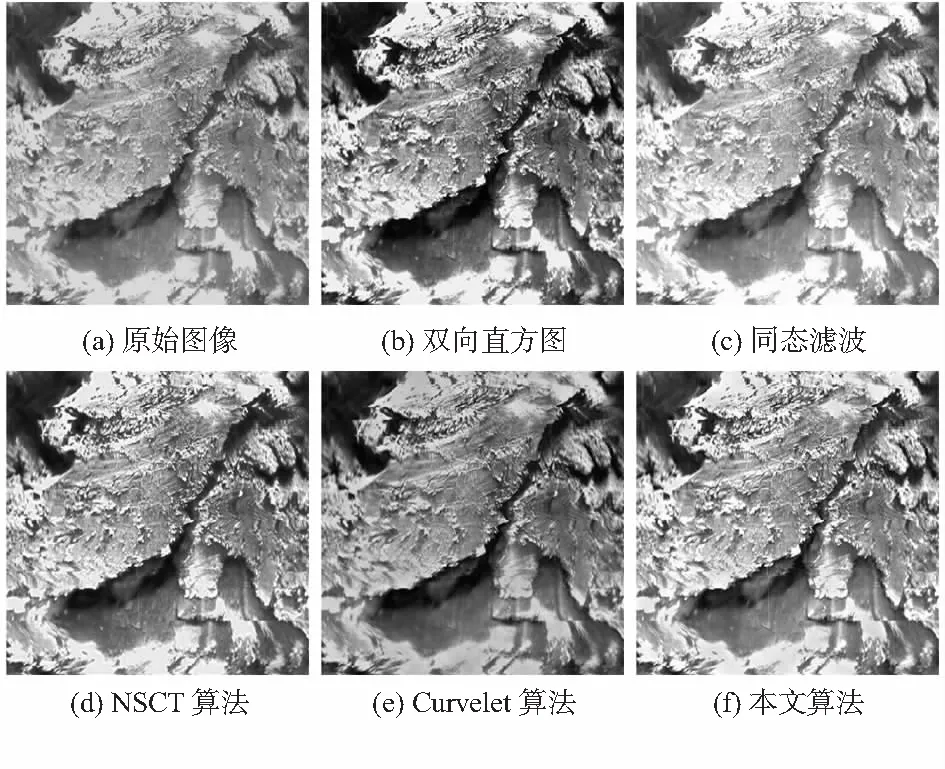
图4 2号场地钻孔图像及5种增强结果
图3(a)、图4(a)分别为1号、2号场地钻孔图像,在“凹槽”内均存在光照不足的问题,细节纹理不够明显且图像整体光照度偏暗对比度低。图3(b),(d),(e)和图4(b),(d),(e)的对比度较原图有所提高,但是“凹槽”内纹理细节依旧无法辨识,例如图3(b),(d),(e)左下角以及图4左上角区域。图3(c)、图4(c)为经过同态滤波处理后的效果图,该方法虽改善了光照不均的问题,然而图像细部分清晰度没有显著提升。图3(f)、图4(f)为本文算法增强结果,增强后的图像较为明亮,对比度较高,无论是外表面还是“凹槽”内纹细节均清晰可见。
为进一步说明实验效果,对实验结果图像进行客观评价。本文选取平均梯度、平均梯度指标、EMEE、对比度作为图像增强质量的评价标准,另外选用运行时间作为算法运行效率的评价标准,分别从增强效果和处理时间2个维度比较各算法的性能。平均梯度的计算公式
(8)
式中Δxf(x,y)=f(x+1,y)-f(x,y);Δyf(x,y)=f(x,y+1)-f(x,y);M和N分别为图像的高度和宽度。
平均梯度指标是用相邻点的差分计算的梯度值,其值越大,图像细节越多,清晰度越高。计算EMEE时,首先将图像f(i,j)划分为k1×k2个相同子块。平均梯度指标的计算公式
(9)
式中 fmax i,j和fmin i,j分别为子块(i,j)中的最大值和最小值;一般取eps=0.000 1,以避免分母过小,子块的大小取为8×8。
EMEE是基于熵的图像对比度增强测量指标,其值往往代表图像一副图像所包含的信息量,其值越大说明图像对比度越高,图像清晰度越高,质量越好。对比度计算公式为
(10)
对比度是衡量一幅图像增强效果的重要指标,对比度值越大,增强后的图像视觉效果越好。
表1中的数据表明,由平均梯度和EMEE指标来看,本文算法对图3的增强效果优于其他4种算法;对图4的增强效果优于同态滤波增强算法、NSCT增强算法、Curvelet增强算法。说明本文算法对图像中岩石表面边缘细节的增强较明显。从对比度指标来看,本文算法的增强效果优于同态滤波增强算法、Curvelet增强算法,略小于NSCT增强算法以及双向直方图增强算法。但是NSCT增强算法耗时较长,不适用于对实时性要求较高的应用场景,而双向直方图则存在过增强的问题,原本“凹槽”内的纹理细节信息丢失更加严重。因而,本文算法无论是从增强效果还是算法效率来看均存在一定优势。

表1 5种增强算法实验结果 s
4 结 论
提出了一种基于同态滤波方法和Curvelet变换系数直方图匹配的钻孔图像自适应增强算法。在Curvelet低频子带部分,将原图系数直方图匹配到经同态滤波后的系数直方图上,使前后两者系数直方图形状近似,达到改善图像光照不均的目的;Curvelet高频子带部分使用自适应增强算法提高图像边缘纹理细节。实验结果表明:算法可以有效地增强钻孔图像中物体的边缘细节,在主观视觉效果和图像客观评价指标上相对于其他算法均有一定优势。
[1] 王川婴,Law K Tim.钻孔摄像技术的发展与现状[C]∥全国地面岩石工程学术会议暨中南地区岩石力学与工程学术会议,2005.
[2] Demirel H,Ozcinar C,Anbarjafari G.Satellite image contrast enhancement using discrete wavelet transform and singular value decomposition[J].IEEE Geoscience & Remote Sensing Letters,2010,7(2):333-337.
[3] Demirel H,Anbarjafari G.Image resolution enhancement by using discrete and stationary wavelet decomposition[J].IEEE Transactions on Image Processing,2011,20(5):1458-1460.
[4] 周 妍,李庆武,霍冠英.基于非下采样Contourlet变换系数直方图匹配的自适应图像增强[J].光学精密工程,2014,22(8):2214-2222.
[5] 沙宇恒,刘 芳,焦李成.基于非下采样Contourlet变换的SAR图像增强[J].电子与信息学报,2009,31(7):1716-1721.
[6] 陈学堂,张 元,杨坤平,等.基于第二代曲波变换算法的检测图像增强[J].传感器与微系统,2008,27(12):8-10.
[7] 盛惠兴,孟凡玲,李庆武,等.Curvelet变换域侧扫声纳图像增强算法[J].海洋测绘,2012,32(1):8-10.
[8] Candes E J,Donoho D L.New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities[J].Communications on Pure and Applied Mathematics,2004,57(2):219-266.
[9] Candes E J,Demanet L,Donoho D L,et al.Fast discrete curvelet transforms[J].Multiscale Modeling & Simulation,2006,5(3):861-899.
[10] 冈萨雷斯.数字图像处理[M].北京:电子工业出版社,2007.
[11] Soyel H,Mcowan P W.Automatic image enhancement using intrinsic geometrical information[J].Electronics Letters,2012,48(15):917-919.
[12] 陈 钱,柏连发,张保民.红外图像直方图双向均衡技术研究[J].红外与毫米波学报,2003,22(6):428-430.
Borehole image adaptive enhancement based on homomorphic filtering and Curvelet transform*
HE Fei-jia1, LI Qing-wu1,2, HAN Hui1, ZHANG Jian-qing3, TAN Xian-jiang3
(1.College of IOT Engineering,HoHai University,Changzhou 213022,China;2.Changzhou Key Laboratory of Sensor Networks and Environmental Sensing,Changzhou 213022,China;3.Changjiang Geophysical Exploration (Wuhan) Co Ltd,Wuhan 430010,China)
To solve problems such as uneven illumination and fuzzy details of rock surface edge are shown in digital borehole images,an adaptive image enhancement algorithm is proposed.Firstly,homomorphic filtering is used to original image.Then,the original image and the filtered image are decomposed by Curvelet transform while the coefficient histogram matching algorithm is used for the low frequency subband of the two.The histogram of the former is matched with the latter to improve effect of illumination unevenness.Next,the high-frequency subband is filtered by an adaptive threshold and is enhanced with an adaptive enhancement function.Finally,the enhanced image is reconstructed by Curvelet inverse transform.The experimental results show that the illumination unevenness is improved effectively and the edge information is enhanced obviously.Certain advantages compared with other algorithms are shown in both subjective and objective evaluation indices.
borehole image; image enhancement; Curvelet transform; coefficient histogram matching; adaptive enhancement
10.13873/J.1000—9787(2017)08—0145—04
2016—12—09
国家自然科学基金资助项目 (41306089); 江苏省重点研发计划资助项目(BE2016056); 常州市科技支撑计划资助项目(CE20150068)
TP 391.41
A
1000—9787(2017)08—0145—04
何飞佳(1992-),男,硕士研究生,研究方向为数字图像处理。
李庆武(1964-),男,通讯作者,教授,博士生导师,研究方向为智能感知与图像处理,E—mail:li_qingwu@163.com。

